Elementos orbitales

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Los elementos orbitales son los parámetros necesarios para identificar de forma única una órbita específica. En mecánica celeste, estos elementos se consideran en sistemas de dos cuerpos utilizando una órbita de Kepler. Hay muchas formas diferentes de describir matemáticamente la misma órbita, pero ciertos esquemas, cada uno de los cuales consta de un conjunto de seis parámetros, se usan comúnmente en astronomía y mecánica orbital.

Una órbita real y sus elementos cambian con el tiempo debido a las perturbaciones gravitatorias de otros objetos y los efectos de la relatividad general. Una órbita de Kepler es una aproximación matemática idealizada de la órbita en un momento determinado.

Elementos keplerianos

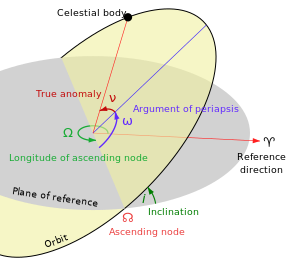
En este diagrama, el plano orbital (amarillo) intersecte un plano de referencia (gray). Para satélites de órbita terrestre, el plano de referencia es generalmente el plano ecuatorial de la Tierra, y para satélites en órbitas solares es el plano eclíptico. La intersección se llama la línea de nodos, ya que conecta el centro de masa con los nodos ascendentes y descendientes. El plano de referencia, junto con el punto vernal (■), establece un marco de referencia.

Los elementos orbitales tradicionales son los seis elementos keplerianos, inspirados en Johannes Kepler y sus leyes del movimiento planetario.

Cuando se ven desde un marco inercial, dos cuerpos en órbita trazan trayectorias distintas. Cada una de estas trayectorias tiene su foco en el centro de masa común. Cuando se ve desde un marco no inercial centrado en uno de los cuerpos, solo es aparente la trayectoria del cuerpo opuesto; Los elementos keplerianos describen estas trayectorias no inerciales. Una órbita tiene dos conjuntos de elementos keplerianos según el cuerpo que se utilice como punto de referencia. El cuerpo de referencia (generalmente el más masivo) se llama primario, el otro cuerpo se llama secundario. El primario no posee necesariamente más masa que el secundario, e incluso cuando los cuerpos son de igual masa, los elementos orbitales dependen de la elección del primario.

Dos elementos definen la forma y el tamaño de la elipse:

Eccentricity (Eccentricity) $e$ ) - Forma de la elipse, describiendo cuánto se alarga en comparación con un círculo (no marcado en el diagrama).
Semimajor axis (Semimajor axis) $a$ ) — la suma de las distancias periapsis y apoapsis divididas por dos. Para las órbitas clásicas de dos cuerpos, el eje semimajor es la distancia entre los centros de los cuerpos, no la distancia de los cuerpos del centro de masa.

Dos elementos definen la orientación del plano orbital en el que se incrusta la elipse:

Inclinación $i$ ) — inclinación vertical de la elipse con respecto al plano de referencia, medido en el nodo ascendente (donde la órbita pasa hacia arriba a través del plano de referencia, el ángulo verde $i$ en el diagrama). El ángulo de inclinación se mide perpendicular a la línea de intersección entre plano orbital y plano de referencia. Cualquier tres puntos en un elipse definirá el plano orbital del elipse. El plano y el elipse son ambos objetos bidimensionales definidos en el espacio tridimensional.
Longitud del nodo ascendente ( $Ω$ ) — oriente horizontalmente el nodo ascendente de la elipse (donde la órbita pasa del sur al norte a través del plano de referencia, simbolizado por $☊$ ) con respecto al punto vernal del marco de referencia (simboizado por ♈). Esto se mide en el plano de referencia, y se muestra como el ángulo verde $Ω$ en el diagrama.

Los dos elementos restantes son los siguientes:

Argumento de periapsis $\cdot$ ) define la orientación de la elipse en el plano orbital, como un ángulo medido desde el nodo ascendente a la periapsis (el punto más cercano que el objeto satélite viene al objeto primario alrededor del cual orbita, el ángulo azul $\cdot$ en el diagrama).
Verdadera anomalía ( $.$ , $Silencio$ , o $f$ En la época $t 0$ ) define la posición del cuerpo orbitante a lo largo de la elipse en un tiempo específico (el "epoch").

La anomalía media $M$ es un "ángulo" ficticio matemáticamente conveniente. que varía linealmente con el tiempo, pero que no corresponde a un ángulo geométrico real. Se puede convertir en la anomalía verdadera $ν$ , que sí representa el ángulo geométrico real en el plano de la elipse, entre periapsis (máxima aproximación al cuerpo central) y la posición del objeto en órbita en un momento dado. Por lo tanto, la verdadera anomalía se muestra como el ángulo rojo $ν$ en el diagrama, y la anomalía media no se muestra.

Los ángulos de inclinación, la longitud del nodo ascendente y el argumento del periapsis también se pueden describir como los ángulos de Euler que definen la orientación de la órbita en relación con el sistema de coordenadas de referencia.

Tenga en cuenta que también existen trayectorias no elípticas, pero no están cerradas y, por lo tanto, no son órbitas. Si la excentricidad es mayor que uno, la trayectoria es una hipérbola. Si la excentricidad es igual a uno y el momento angular es cero, la trayectoria es radial. Si la excentricidad es uno y hay momento angular, la trayectoria es una parábola.

Parámetros requeridos

Dado un marco de referencia inercial y una época arbitraria (un punto específico en el tiempo), se necesitan exactamente seis parámetros para definir sin ambigüedades una órbita arbitraria y sin perturbaciones.

Esto se debe a que el problema contiene seis grados de libertad. Estos corresponden a las tres dimensiones espaciales que definen la posición ( $x$ , $y$ , $z$ en un sistema de coordenadas cartesianas), más la velocidad en cada una de estas dimensiones. Estos pueden describirse como vectores de estado orbital, pero a menudo es una forma inconveniente de representar una órbita, razón por la cual los elementos keplerianos se usan comúnmente en su lugar.

A veces, la época se considera un "séptimo" parámetro orbital, en lugar de ser parte del marco de referencia.

Si la época se define como el momento en que uno de los elementos es cero, el número de elementos no especificados se reduce a cinco. (El sexto parámetro sigue siendo necesario para definir la órbita; simplemente se establece numéricamente en cero por convención o se "mueve" a la definición de la época con respecto al tiempo del reloj del mundo real).

Parametrizaciones alternativas

Los elementos keplerianos se pueden obtener a partir de vectores de estado orbital (un vector tridimensional para la posición y otro para la velocidad) mediante transformaciones manuales o con programas informáticos.

Se pueden calcular otros parámetros orbitales a partir de los elementos keplerianos, como el período, el apoapsis y el periapsis. (Al orbitar la Tierra, los dos últimos términos se conocen como apogeo y perigeo). Es común especificar el período en lugar del semieje mayor en los conjuntos de elementos keplerianos, ya que cada uno se puede calcular a partir del otro siempre que el estándar gravitacional. El parámetro, $GM$ , se proporciona para el cuerpo central.

En lugar de la anomalía media en la época, la anomalía media $M$ , longitud media, anomalía verdadera $ν 0$ , o (rara vez) se puede usar la anomalía excéntrica.

Utilizando, por ejemplo, la "anomalía media" en lugar de "anomalía media en la época" significa que el tiempo $t$ debe especificarse como un séptimo elemento orbital. A veces se supone que la anomalía media es cero en la época (eligiendo la definición apropiada de la época), dejando solo los otros cinco elementos orbitales por especificar.

Se utilizan diferentes conjuntos de elementos para varios cuerpos astronómicos. La excentricidad, $e$ , y el semieje mayor, $a$ , o la distancia del periapsis, $q$ , se utilizan para especificar la forma y el tamaño de una órbita. La longitud del nodo ascendente, $Ω$ , la inclinación, $i$ , y el argumento de periapsis, $ω$ , o la longitud de periapsis, $ϖ$ , especifique la orientación de la órbita en su plano. La longitud en la época, $L 0$ , la anomalía media en la época, $< i>M 0$ , o el momento del paso del perihelio, $T 0$ , se utilizan para especificar un punto conocido en la órbita. Las elecciones realizadas dependen de si se utiliza el equinoccio vernal o el nodo como referencia principal. El semieje mayor se conoce si se conocen el movimiento medio y la masa gravitatoria.

También es bastante común ver la anomalía media ( $M$ ) o la longitud media ( $L$ ) expresado directamente, sin $M 0 < /span> o L 0 como pasos intermedios, como una función polinómica con respecto al tiempo. Este método de expresión consolidará el movimiento medio (n) en el polinomio como uno de los coeficientes. La apariencia será L o M se expresan de una manera más complicada, pero parecerá que necesitamos un elemento orbital menos.$

El movimiento medio también se puede oscurecer detrás de las citas del período orbital $P$ .

Conjuntos de elementos orbitales
Objeto	Elementos utilizados
Planeta Mayor	$e, a, i, Ω, π, L0$
Comet	$e, q, i, Ω, ω, T 0$
Asteroid	$e, a, i Ω, ω, M0$
Elementos de dos líneas	$e, i, Ω, \cdot, n, M 0$

Transformaciones del ángulo de Euler

Los ángulos $Ω$ , $i$ , $ω$ son los ángulos de Euler (correspondientes a $α$ , $β$ , $γ$ en la notación utilizada en ese artículo) que caracteriza la orientación del sistema de coordenadas

$x̂$ , $.$ , $ẑ$ del marco de coordinación inercial $Î$ , $Ĵ$ , $K̂$

donde:

$Î$ , $Ĵ$ está en el plano ecuatorial del cuerpo central. $Î$ está en la dirección del equinoccio vernal. $Ĵ$ es perpendicular a $Î$ y con $Î$ define el plano de referencia. $K̂$ es perpendicular al plano de referencia. Elementos orbitales de cuerpos (planetas, cometas, asteroides,...) en el Sistema Solar generalmente el eclíptico como ese plano.
$x̂$ , $.$ están en el plano orbital y con $x̂$ en la dirección al pericenter (periapsis). $ẑ$ es perpendicular al plano de la órbita. $.$ es mutuamente perpendicular a $x̂$ y $ẑ$ .

Entonces, la transformación de $Î$ , $Ĵ$ , $K̂$ marco de coordenadas a $x̂$ , < span class="texhtml">ŷ, $ẑ$ marco con los ángulos de Euler $Ω$ , $i$ , $ω$ es:

{displaystyle {begin{aligned}x_{1} Omega cdot cos omega -sin Omega cdot cos icdot sin omega ;x_{2} limit=sin Omega cdot cos omega +cos Omega cdot cos icdot sin omega ;x_{3} limit=sin icdot sin omega;\\\,\y_{1} limit=-cos Omega cdot sin omega -sin Omega cdot cos icdot cos omega ;y_{2} Omega cdot sin omega +cos Omega cdot cos icdot cos omega ;\y_{3} limit=sin icdot cos omega ;\\\,\z_{1} limit=cdot sin Omega ;z_{2} Omega ;z_{3} {=cos i;\end{aligned}}}

{displaystyle {begin{bmatrix}x_{1} limitx_{2} limitx_{3}\\y_{1} limity_{2} {3}z_{1} limitz_{2} limites_{3}end{bmatrix}}={begin{bmatrix}cos omegaomega {begin{bmatrix}0},{begin{bmatrix}1 âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa âTMa {bmatrix},{begin{bmatrix}cos Omega &sin Omega &0\-sin Omega &cos Omega &0

Elementos orbitales

Elementos keplerianos

Parámetros requeridos

Parametrizaciones alternativas

Transformaciones del ángulo de Euler

Contenido relacionado