Elemento inverso

Compartir Imprimir Citar

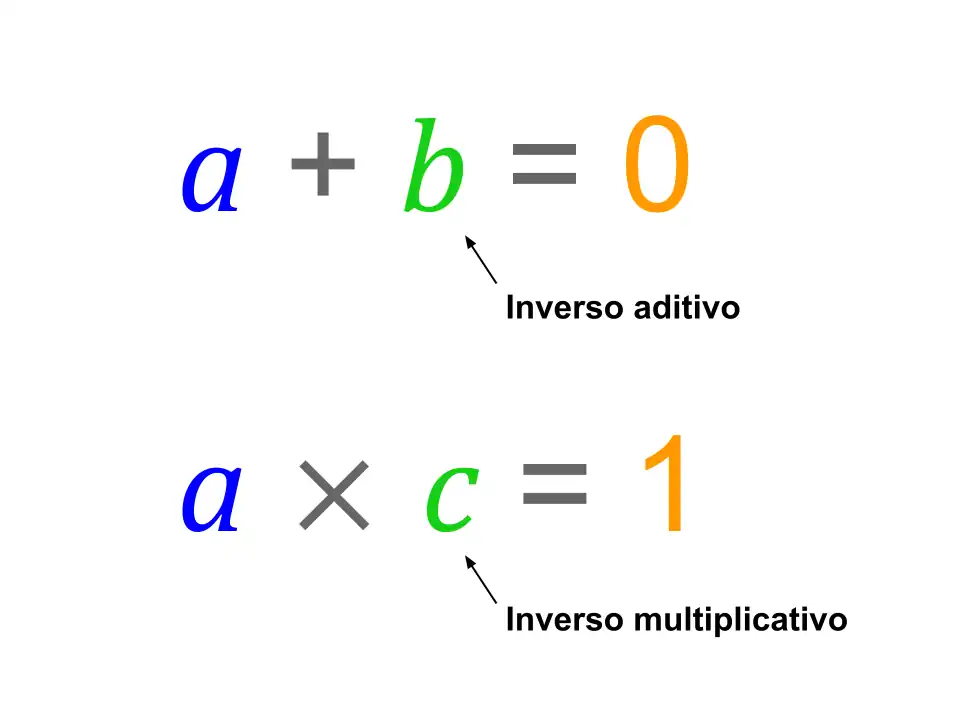
Inversos aditivo y multiplicativo — Ejemplo del inverso aditivo y multiplicativo

Un elemento inverso es aquel que dentro de una operación binaria bien definida da como resultado el elemento neutro de dicha operación, 0 en el caso de la adición, y 1 en el caso de la multiplicación. En la práctica, el concepto de elemento inverso engloba al inverso aditivo (−x) denominado también opuesto o simétrico, y al inverso multiplicativo (1/x) denominado también recíproco. Este concepto es fundamental en las matemáticas y se aplica especialmente a las operaciones de suma y multiplicación, aunque teóricamente cualquier elemento que cumpla su planteamiento es un inverso.

En el contexto de una operación, denotada aquí como ∗, y un elemento neutro (o de identidad), indicado como e, se establece que si x ∗ y = e, entonces x es un inverso a la izquierda de y, mientras que y es un inverso a la derecha de x. Cabe destacar que un elemento neutro es aquel que cumple la premisa de que x ∗ e = x y también e ∗ y = y para todos los valores de x y y donde la operación binaria sea previamente bien definida.

Cuando la operación ∗ es asociativa, y un elemento x posee tanto un inverso izquierdo como un inverso derecho, estos inversos son iguales y únicos. Este único inverso se conoce simplemente como el elemento inverso o el inverso de x. Es común especificar la operación a la que se refiere el inverso, utilizando términos como en el caso de el inverso aditivo, el inverso multiplicativo o el inverso funcional. En operaciones asociativas, un elemento que posee un inverso se denomina elemento invertible.

Los elementos inversos son ampliamente utilizados en otras estructuras matemáticas como los grupos y los anillos. En los grupos, cada elemento es invertible, mientras que en los anillos, los elementos invertibles se conocen como unidades. Además, los inversos son esenciales en operaciones que no están definidas para todos los operandos, como es el caso de las matrices inversas y las funciones inversas. La aplicación del concepto de elemento inverso se ha extendido también a la teoría de categorías. En este ámbito, un isomorfismo se define como un morfismo invertible, demostrando la versatilidad y relevancia del concepto de inverso.

La palabra 'inverso' proviene del latín inversus, que significa 'volteado hacia abajo' o 'revertir'. Originalmente el elemento inverso fue la denominación del inverso multiplicativo, mientras que el elemento simétrico fue la denominación del inverso aditivo, pero conforme el concepto se expandió a otras áreas de las matemáticas y se unificó en una sola definición junto a otro tipo de operaciones como las funciones inversas, terminó por adoptarse la palabra inverso para definir a cualquier elemento que cumpliera con el enunciado de los inversos. Su origen dentro de los inversos multiplicativos está relacionado con las fracciones, donde el inverso multiplicativo se obtiene intercambiando el numerador y el denominador (por ejemplo, el inverso de x/y es y/x).

HSD

Definiciones y propiedades básicas

Los conceptos de elemento inverso y elemento invertible se definen comúnmente para operaciones binarias que están definidas en todas partes (es decir, la operación se define para dos elementos cualesquiera de su dominio). Sin embargo, estos conceptos se usan comúnmente con operaciones parciales, es decir, operaciones que no están definidas en todas partes. Ejemplos comunes son la multiplicación de matrices, la composición de funciones y la composición de morfismos en una categoría. De ello se deduce que las definiciones comunes de asociatividad y elemento de identidad deben extenderse a las operaciones parciales; este es el objeto de los primeros incisos.

En esta sección, $X$ es un conjunto (posiblemente una clase adecuada) en el que se define una operación parcial (posiblemente total), que se denota con ${displaystyle *.}$

Asociatividad

Una operación parcial es asociativa si

{displaystyle x*(y*z)=(x*y)*z}

para cada $x, y, z$ en $X$ para la que se define uno de los miembros de la igualdad; la igualdad significa que el otro miembro de la igualdad también debe ser definido.

Ejemplos de operaciones asociativas no totales son la multiplicación de matrices de tamaño arbitrario y la composición de funciones.

Elementos de identidad o neutro

Vamos $*$ ser una operación asociativa posiblemente parcial en un conjunto $X$ .

Un elemento de identidad, o simplemente una identidad es un elemento $e tal que$

{displaystyle x*e=xquad {text{and}}quad e*y=y}

para cada $x$ y $y$ para los que se definen los lados izquierdos de las igualdades.

Si $e$ y $f$ son dos elementos de identidad tales que ${displaystyle e*f}$ se define, entonces ${displaystyle e=f.}$ (Esto resulta inmediatamente de la definición, por ${displaystyle e=e*f=f.}$ )

De ello se desprende que una operación total tiene en la mayoría de un elemento de identidad, y si $e$ y $f$ son diferentes identidades, entonces ${displaystyle e*f}$ no se define.

Por ejemplo, en el caso de la multiplicación de matrices, hay una matriz identidad $n \times n$ para cada matriz positiva entero $n$ , y dos matrices de identidad de diferente tamaño no se pueden multiplicar juntas.

Del mismo modo, las funciones de identidad son elementos de identidad para la composición de funciones, y la composición de las funciones de identidad de dos conjuntos diferentes no está definida.

Inversos izquierdo y derecho

Si ${displaystyle x*y=e,}$ Donde $e$ es un elemento de identidad, uno dice que $x$ es un izquierda inversa de $Sí.$ , y $Sí.$ es un derecho inverso de $x$ .

No siempre existen los inversos izquierdo y derecho, incluso cuando la operación es total y asociativa. Por ejemplo, la suma es una operación asociativa total en enteros no negativos, que tiene $0$ como identidad aditiva, y $0$ es el único elemento que tiene un inverso aditivo. Esta falta de inversos es la principal motivación para extender los números naturales a los enteros.

Un elemento puede tener varios inversos izquierdos y varios inversos derecho, incluso cuando la operación es total y asociativa. Por ejemplo, considere las funciones de los enteros a los enteros. El función duplicadora ${displaystyle xmapsto 2x}$ tiene infinitamente muchos inversos izquierdos bajo la composición de la función, que son las funciones que dividen por dos los números uniformes, y dan cualquier valor a números impares. Del mismo modo, cada función que mapea $n$ a ambos $2n$ o $2n+1$ es un inverso derecho de la función ${textstyle nmapsto leftlfloor {frac {n}{2}}rightrfloor}$ la función del suelo que mapas $n$ a ${textstyle {frac {n}{2}}}$ o ${textstyle {frac {n-1}{2}},}$ dependiendo de si $n$ es incluso o extraño.

Más generalmente, una función tiene inversa izquierda para la composición de funciones si y solo si es inyectiva, y tiene inversa derecha si y solo si es sobreyectiva.

En la teoría de categorías, los inversos a la derecha también se denominan secciones, y los inversos a la izquierda se denominan retracciones.

Inversos

Un elemento es invertible bajo una operación si tiene un inverso izquierdo y un inverso derecho.

En el caso común donde la operación es asociativa, el inverso izquierdo y derecho de un elemento son iguales y únicos. De hecho, si $l$ y $r$ son respectivamente un inverso izquierdo y un inverso derecho de $x$ , entonces

{displaystyle l=l*(x*r)=(l*x)*r=r.}

El inverso de un elemento invertible es su único inverso izquierdo o derecho.

Si la operación se denota como adición, el inverso inverso o aditivo, de un elemento $x$ es denotado ${displaystyle -x.}$ De lo contrario, el inverso de $x$ es generalmente denotado ${displaystyle x^{-1},}$ o, en el caso de una multiplicación conmutativa ${textstyle {frac {1}{x}}.}$ Cuando puede haber una confusión entre varias operaciones, el símbolo de la operación se puede añadir antes del exponente, como en ${displaystyle x^{*-1}.}$ La notación ${displaystyle f^{circ -1}}$ no se utiliza comúnmente para la composición de la función, ya que ${textstyle {frac {1}{f}}}$ se puede utilizar para el inverso multiplicativo.

Si $x$ y $Sí.$ son invertibles, y $x*y$ se define, entonces $x*y$ es invertible, y su inverso es ${displaystyle y^{-1}x^{-1}.}$

Un homomorfismo invertible se llama isomorfismo. En
teoría de categorías, un morfismo invertible también se llama isomorfismo.

Dentro de grupos

Un grupo es un conjunto con una operación asociativa que tiene un elemento de identidad, y para el cual cada elemento tiene un inverso.

Así, la inversa es una función del grupo a sí mismo que también puede ser considerada como una operación de aridad uno. También es una involución, ya que el inverso del inverso de un elemento es el elemento mismo.

Un grupo puede actuar en un conjunto como transformaciones de este conjunto. En este caso, el inverso $g^{-1}$ de un elemento de grupo $g$ define una transformación que es el inverso de la transformación definida por ${displaystyle g,}$ es decir, la transformación que "no hace" la transformación definida por $g.$

Por ejemplo, el grupo de cubos de Rubik representa las secuencias finitas de movimientos elementales. El inverso de tal secuencia se obtiene aplicando el inverso de cada movimiento en el orden inverso.

Dentro de monoides

Un monoide es un conjunto con una operación asociativa que tiene un elemento de identidad.

Los elementos invertibles en un monoide forman un grupo bajo operación monoide.

Un anillo es un monoide para la multiplicación de anillos. En este caso, los elementos invertibles también se denominan unidades y forman el grupo de unidades del anillo.

Si un monoide no es conmutativo, pueden existir elementos no invertibles que tengan un inverso a la izquierda o un inverso a la derecha (no ambos, ya que, de lo contrario, el elemento sería invertible).

Por ejemplo, el conjunto de funciones de un conjunto a sí mismo es un monoide bajo composición de funciones. En este monoide, los elementos invertibles son las funciones biyectivas; los elementos que tienen inversas por la izquierda son las funciones inyectivas, y los que tienen inversas por la derecha son las funciones sobreyectivas.

Dado un monoide, uno puede querer extenderlo agregando inverso a algunos elementos. Esto es generalmente imposible para los monoides no conmutativos, pero, en un monoide comunitario, es posible añadir inversos a los elementos que tienen la propiedad de cancelación (un elemento) $x$ tiene la propiedad de cancelación si ${displaystyle xy=xz}$ implicación ${displaystyle y=z,}$ y ${displaystyle yx=zx}$ implicación $y=z$ ). Esta extensión de un monoide está permitida por la construcción del grupo Grothendieck. Este es el método que se utiliza comúnmente para construir números naturales, números racionales de números enteros y, más generalmente, el campo de fracciones de un dominio integral, y localizaciones de anillos conmutativos.

Dentro de anillos

Un anillo es una estructura algebraica con dos operaciones, suma y multiplicación, que se denotan como las operaciones habituales con números.

Bajo suma, un anillo es un grupo abeliano, lo que significa que la suma es conmutativa y asociativa; tiene una identidad, llamada identidad aditiva, y se denota $0$ ; y cada elemento $x$ tiene un inverso, llamado su inverso aditivo y denotado $- x$ . Debido a la conmutatividad, los conceptos de inversas izquierda y derecha no tienen sentido ya que no difieren de las inversas.

Bajo la multiplicación, un anillo es un monoide; esto significa que la multiplicación es asociativa y tiene una identidad llamada la identidad multiplicativa y denotada $1$ . An elemento invertible para la multiplicación se llama unidad. El inverso inverso o multiplicador (para evitar confusión con inversos aditivos) de una unidad $x$ es denotado ${displaystyle x^{-1},}$ o, cuando la multiplicación es conmutativa, ${textstyle {frac {1}{x}}.}$

La identidad aditiva $0$ nunca es una unidad, excepto cuando el anillo es el cero, que tiene $0$ como su elemento único

Si $0$ es el único elemento que no es unidad, el anillo es un campo si la multiplicación es conmutativa, o un anillo de división en caso contrario.

En un anillo no conmutativo (es decir, un anillo cuya multiplicación no es conmutativa), un elemento no invertible puede tener uno o varios inversos a la izquierda o a la derecha. Este es, por ejemplo, el caso de las funciones de los enteros a sí mismos, que forman un anillo para operaciones puntuales; ver arriba, § Inversos izquierdo y derecho.

Un anillo conmutativo (es decir, un anillo cuya multiplicación es conmutativa) se puede ampliar añadiendo inversos a elementos que no son divisores de cero (es decir, su producto con un elemento distinto de cero no puede ser $0$ ). Este es el proceso de localización, que produce, en particular, el campo de los números racionales a partir del anillo de los enteros y, más generalmente, el campo de las fracciones de un dominio integral. La localización también se usa con divisores de cero, pero, en este caso, el anillo original no es un subanillo de la localización; en cambio, se asigna de forma no inyectiva a la localización.

Dentro de Matrices

La multiplicación de matrices se define comúnmente para matrices sobre un campo y se extiende directamente a matrices sobre anillos, rngs y semirings. Sin embargo, en esta sección, solo se consideran matrices sobre un anillo conmutativo, debido al uso del concepto de rango y determinante.

Si $A$ es un $m \times n$ matriz (es decir, una matriz con $m$ filas y $n$ columnas), y $B$ es una p×q matriz, el producto $AB$ se define si $n = p$ , y solo en este caso. Una matriz identidad, es decir, un elemento identidad para la multiplicación de matrices es una matriz cuadrada (mismo número para filas y columnas) cuyas entradas de la diagonal principal son todas iguales a $1$ , y todas las demás entradas son $0$ .

Una matriz invertible es un elemento invertible bajo la multiplicación de matrices. Una matriz sobre un anillo conmutativo $R$ es invertible si y solo si su determinante es una unidad en $R$ (es decir, es invertible en $R$ . En este caso, su matriz inversa se puede calcular con la regla de Cramer.

Si $R$ es un campo, el determinante es invertible si y solo si no es cero. Como el caso de los campos es más común, a menudo se ven matrices invertibles definidas como matrices con un determinante distinto de cero, pero esto es incorrecto sobre anillos.

En el caso de matrices enteras (es decir, matrices con entradas enteras), una matriz invertible es una matriz que tiene una inversa que también es una matriz entera. Tal matriz se llama matriz unimodular para distinguirla de las matrices que son invertibles sobre los números reales. Una matriz de enteros cuadrados es unimodular si y solo si su determinante es $1$ o $-1$ , ya que estos dos números son las únicas unidades en el anillo de los enteros.

Una matriz tiene inversa por la izquierda si y solo si su rango es igual a su número de columnas. Este inverso izquierdo no es único, excepto para matrices cuadradas donde el inverso izquierdo es igual a la matriz inversa. De manera similar, existe un inverso derecho si y solo si el rango es igual al número de filas; no es única en el caso de una matriz rectangular, y es igual a la matriz inversa en el caso de una matriz cuadrada.

Funciones, homomorfismos y morfismos

La composición es una operación parcial que se generaliza a homomorfismos de estructuras algebraicas y morfismos de categorías en operaciones que también se denominan composición y comparten muchas propiedades con la composición de funciones.

En todos los casos, la composición es asociativa.

Si $fcolon Xto Y$ y ${displaystyle gcolon Y'to Z,}$ la composición $gcirc f$ se define si y sólo si ${displaystyle Y'=Y}$ o, en los casos de función y homomorfismo, ${displaystyle Ysubset Y'.}$ En los casos de función y homomorfismo, esto significa que el codominio de $f$ igual o se incluye en el dominio de $g$ . En el caso del morfismo, esto significa que el codominio $f$ iguala el dominio de $g$ .

Hay una identidad ${displaystyle operatorname {id} _{X}colon Xto X}$ para cada objeto $X$ (set, estructura algebraica o objeto), que se llama también una función de identidad en el caso de la función.

Una función es invertible si y solo si es una biyección. Un homomorfismo o morfismo invertible se llama isomorfismo. Un homomorfismo de estructuras algebraicas es un isomorfismo si y solo si es una biyección. La inversa de una biyección se llama función inversa. En los demás casos, se habla de isomorfismos inversos.

Una función tiene inversa izquierda o inversa derecha si y solo es inyectiva o sobreyectiva, respectivamente. Un homomorfismo de estructuras algebraicas que tiene un inverso a la izquierda o un inverso a la derecha es respectivamente inyectivo o sobreyectivo, pero lo contrario no es cierto en algunas estructuras algebraicas. Por ejemplo, lo contrario es cierto para espacios vectoriales pero no para módulos sobre un anillo: un homomorfismo de módulos que tiene un inverso a la izquierda de un inverso a la derecha se denomina respectivamente epimorfismo dividido o monomorfismo dividido. Esta terminología también se usa para morfismos en cualquier categoría.

Generalizaciones

En un magma unitario

Vamos $S$ ser un magma unitario, es decir, un conjunto con una operación binaria $*$ y un elemento de identidad ${displaystyle ein S}$ . Si, para $a,bin S$ , tenemos $a*b=e$ , entonces $a$ se llama izquierda inversa de $b$ y $b$ se llama derecho inverso de $a$ . Si un elemento $x$ es un inverso izquierdo y un inverso derecho $y$ , entonces $x$ se llama dos caras inversas, o simplemente un inverso, de $y$ . Un elemento con un inverso de dos caras $S$ se llama invertible dentro $S$ . Un elemento con un elemento inverso sólo en un lado es izquierda invertible o derecho invertido.

Elementos de un magma unitario $(S,*)$ puede tener múltiples inversos izquierdo, derecho o de dos caras. Por ejemplo, en el magma dado por la tabla Cayley

*	1	2	3
1	1	2	3
2	2	1	1
3	3	1	1

los elementos 2 y 3 tienen cada uno dos inversos de dos lados.

Un magma unitario en el que todos los elementos son invertibles no necesita ser un bucle. Por ejemplo, en el magma $(S,*)$ dada por la mesa de Cayley

*	1	2	3
1	1	2	3
2	2	1	2
3	3	2	1

cada elemento tiene un inverso único de dos caras (nombre mismo), pero $(S,*)$ no es un bucle porque la mesa de Cayley no es una plaza latina.

Del mismo modo, un ciclo no necesita tener inversas de dos lados. Por ejemplo, en el ciclo dado por la tabla de Cayley

*	1	2	3	4	5
1	1	2	3	4	5
2	2	3	1	5	4
3	3	4	5	1	2
4	4	5	2	3	1
5	5	1	4	2	3

el único elemento con un inverso de dos lados es el elemento de identidad 1.

Si la operación $*$ es asociativo entonces si un elemento tiene un inverso izquierdo y un inverso derecho, son iguales. En otras palabras, en un monoide (un magma unitario asociativo) cada elemento tiene en la mayoría de un inverso (como se define en esta sección). En un monoide, el conjunto de elementos invertibles es un grupo, llamado el grupo de unidades de $S$ , y denotado por $U(S)$ o H₁.

En un semigrupo

La definición de la sección anterior generaliza la noción de inverso en grupo relativa a la noción de identidad. También es posible, aunque menos obvio, generalizar la noción de un inverso eliminando el elemento de identidad pero manteniendo la asociatividad; es decir, en un semigrupo.

En un semigrupo S un elemento x se llama (von Neumann) regular si existe algún elemento z en S tal que xzx = x; z a veces se denomina pseudoinverse. Un elemento y se llama (simplemente) un inverso de x si xyx = x y y = yxy. Todo elemento regular tiene al menos un inverso: si x = xzx entonces es fácil verificar que y = zxz es un inverso de x como se define en esta sección. Otro hecho fácil de probar: si y es un inverso de x entonces e = xy y f = yx son idempotentes, es decir ee = e y ff = f. Así, cada par de elementos (mutuamente) inversos da lugar a dos idempotentes, y ex = xf = x, ye = fy = y, y e actúa como una identidad izquierda en x, mientras que f actúa como una identidad correcta, y los roles izquierdo/derecho se invierten para y. Esta simple observación se puede generalizar usando las relaciones de Green: cada e idempotente en un semigrupo arbitrario es una identidad izquierda para R_e y identidad correcta para L_e. Una descripción intuitiva de este hecho es que cada par de elementos mutuamente inversos produce una identidad local izquierda y, respectivamente, una identidad local derecha.

En un monoide, la noción de inversa como se define en la sección anterior es estrictamente más estrecha que la definición dada en esta sección. Solo los elementos de la clase verde H1 tienen un inverso desde la perspectiva del magma unitario, mientras que para cualquier idempotente e, los elementos de H_e tienen un inversa como se define en esta sección. Bajo esta definición más general, los inversos no necesitan ser únicos (o existir) en un semigrupo o monoide arbitrario. Si todos los elementos son regulares, entonces el semigrupo (o monoide) se llama regular y cada elemento tiene al menos un inverso. Si cada elemento tiene exactamente un inverso como se define en esta sección, entonces el semigrupo se llama semigrupo inverso. Finalmente, un semigrupo inverso con un solo idempotente es un grupo. Un semigrupo inverso puede tener un elemento absorbente 0 porque 000 = 0, mientras que un grupo puede no tenerlo.

Fuera de la teoría de semigrupos, un inverso único como se define en esta sección a veces se denomina cuasi-inverso. En general, esto se justifica porque en la mayoría de las aplicaciones (por ejemplo, todos los ejemplos de este artículo) se mantiene la asociatividad, lo que hace que esta noción sea una generalización del inverso izquierdo/derecho en relación con una identidad (consulte Inverso generalizado).

U-semigrupos

Una generalización natural del semigrupo inverso es definir una operación unaria (arbitraria) ° tal que (a°)° = a para todo a en S; esto dota a S de un álgebra de tipo ⟨2,1⟩. Un semigrupo dotado de tal operación se denomina U-semigrupo. Aunque pueda parecer que a° será el inverso de a, este no es necesariamente el caso. Para obtener nociones interesantes, la operación unaria debe interactuar de alguna manera con la operación de semigrupo. Se han estudiado dos clases de semigrupos U:

I- semigrupos, en el cual el axioma de interacción es aa°a = a
*-semigroups, en el que el axioma de interacción es (ab)° = b°a°. Tal operación se llama una involución, y típicamente denotada por a*

Claramente, un grupo es tanto un semigrupo I como un semigrupo *. Una clase de semigrupos importante en la teoría de semigrupos son los semigrupos completamente regulares; estos son I-semigrupos en los que además se tiene aa° = a°a; en otras palabras, cada elemento tiene conmutación pseudoinverse a°. Sin embargo, hay pocos ejemplos concretos de tales semigrupos; la mayoría son semigrupos completamente simples. Por el contrario, una subclase de semigrupos *, los semigrupos regulares * (en el sentido de Drazin), producen uno de los ejemplos más conocidos de un pseudoinverso (único), el inverso de Moore-Penrose. En este caso, sin embargo, la involución a* no es la pseudoinversa. Más bien, el pseudoinverso de x es el único elemento y tal que xyx = x, yxy = y, (xy)* = xy, (yx)* = yx . Dado que los semigrupos *-regulares generalizan semigrupos inversos, el único elemento definido de esta manera en un semigrupo *-regular se denomina inverso generalizado o inverso de Moore-Penrose.

Semianillos

Ejemplos

Todos los ejemplos en esta sección involucran operadores asociativos.

Conexiones Galois

Los adjuntos inferior y superior en una conexión de Galois (monótona), L y G son casi inversos entre sí; es decir, LGL = L y GLG = G y uno determina de forma única al otro. Sin embargo, no son inversos izquierdos o derechos uno del otro.

Inversos generalizados de matrices

Una matriz cuadrada $M$ con entradas en un campo $K$ es invertible (en el conjunto de todas las matrices cuadradas del mismo tamaño, bajo multiplicación de matriz) si y sólo si su determinante es diferente a cero. Si el determinante $M$ es cero, es imposible que tenga un inverso unilateral; por lo tanto un inverso izquierdo o derecho implica la existencia del otro. Ver matriz invertible para más.

Más generalmente, una matriz cuadrada sobre un anillo conmutativo $R$ es invertible si y sólo si su determinante es invertible $R$ .

Las matrices no cuadradas de rango completo tienen varias inversas unilaterales:

Para $n}" xmlns="http://www.w3.org/1998/Math/MathML">A:m× × n▪ ▪ m■n{displaystyle A:mtimes nmid m títulon}n" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7a0d7f97b541f8b914eecf9f0fce2147f9ad2331" style="vertical-align: -0.838ex; width:18.427ex; height:2.843ex;"/>$ hemos dejado inversos; por ejemplo, ${displaystyle underbrace {left(A^{text{T}}Aright)^{-1}A^{text{T}}} _{A_{text{left}}^{-1}}A=I_{n}}$
Para $<math alttext="{displaystyle A:mtimes nmid mA:m\times \times n▪ ▪ m.n{displaystyle A:mtimes nmid m maden} <img alt="A:mtimes nmid m$ tenemos inversos correctos; por ejemplo, ${displaystyle Aunderbrace {A^{text{T}}left(AA^{text{T}}right)^{-1}} _{A_{text{right}}^{-1}}=I_{m}}$

El inverso izquierdo se puede utilizar para determinar la menor solución de norma $Ax=b$ , que es también la fórmula menos cuadrado para la regresión y se da por ${displaystyle x=left(A^{text{T}}Aright)^{-1}A^{text{T}}b.}$

Ninguna matriz de rango deficiente tiene inversa (ni siquiera unilateral). Sin embargo, la inversa de Moore-Penrose existe para todas las matrices y coincide con la inversa izquierda o derecha (o verdadera) cuando existe.

Como ejemplo de matriz inversa, considere:

{displaystyle A:2times 3={begin{bmatrix}1&2&3\4&5&6end{bmatrix}}}

Así que, como m. n, tenemos un inverso derecho, ${displaystyle A_{text{right}}^{-1}=A^{text{T}}left(AA^{text{T}}right)^{-1}.}$ Por componentes se calcula como

{displaystyle {begin{aligned}AA^{text{T}}&={begin{bmatrix}1&2&3\4&5&6end{bmatrix}}{begin{bmatrix}1&4\2&5\3&6end{bmatrix}}={begin{bmatrix}14&32\32&77end{bmatrix}}\[3pt]left(AA^{text{T}}right)^{-1}&={begin{bmatrix}14&32\32&77end{bmatrix}}^{-1}={frac {1}{54}}{begin{bmatrix}77&-32\-32&14end{bmatrix}}\[3pt]A^{text{T}}left(AA^{text{T}}right)^{-1}&={frac {1}{54}}{begin{bmatrix}1&4\2&5\3&6end{bmatrix}}{begin{bmatrix}77&-32\-32&14end{bmatrix}}={frac {1}{18}}{begin{bmatrix}-17&8\-2&2\13&-4end{bmatrix}}=A_{text{right}}^{-1}end{aligned}}}

La inversa izquierda no existe, porque

{displaystyle A^{text{T}}A={begin{bmatrix}1&4\2&5\3&6end{bmatrix}}{begin{bmatrix}1&2&3\4&5&6end{bmatrix}}={begin{bmatrix}17&22&27\22&29&36\27&36&45end{bmatrix}}}

que es una matriz singular y no se puede invertir.