Elemento de simetría
En química y cristalografía, un elemento de simetría es un punto, línea o plano sobre el cual pueden tener lugar operaciones de simetría. En particular, un elemento de simetría puede ser un plano de espejo, un eje de rotación (propio o impropio) o un centro de inversión. Para un objeto como una molécula o un cristal, un elemento de simetría corresponde a un conjunto de operaciones de simetría, que son las transformaciones rígidas que emplean el elemento de simetría y que dejan el objeto inalterado. El conjunto que contiene estas operaciones forma uno de los grupos de simetría del objeto. Los elementos de este grupo de simetría no deben confundirse con el propio "elemento de simetría". En términos generales, un elemento de simetría es el conjunto geométrico de puntos fijos de una operación de simetría. Por ejemplo, para la rotación sobre un eje, los puntos del eje no se mueven y, en una reflexión, los puntos que permanecen inalterados forman un plano de simetría.
Identidad
El elemento de simetría identidad se encuentra en todos los objetos y se denota E. Corresponde a una operación de no hacer nada al objeto. Como cada molécula es indistinguible de sí misma si no se le hace nada, cada objeto posee al menos el elemento identidad. Un objeto que no tiene otros elementos de simetría que E se llama asimétrico. Un objeto de este tipo es necesariamente quiral.
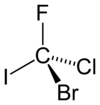
Una molécula de bromoclorofluoroiododododometano es asimétrica: no tiene simetrías excepto la identidad.
Aviones espejo
Los planos especulares se denotan por σ. En una molécula que también tiene un eje de simetría, un plano especular que incluye el eje se denomina plano especular vertical y se etiqueta como σv, mientras que uno perpendicular al eje se denomina plano especular horizontal y se etiqueta como σh. Un plano especular vertical que biseca el ángulo entre dos ejes C2 se denomina plano especular diedro, σd.

Simetría rotacional
La simetría rotacional, también conocida como simetría radial, se representa mediante un eje alrededor del cual gira el objeto en su operación de simetría correspondiente. Un grupo de rotaciones propias se denota como Cn, donde los grados de rotación que restauran el objeto son 360/n (C2= rotación de 180º, C3= rotación de 120º, C4= rotación de 90º, C5= rotación de 72º). La notación Cn también se utiliza para el grupo cíclico relacionado, más abstracto.
Una rotación impropia es la composición de una rotación sobre un eje y una reflexión en un plano perpendicular a ese eje. El orden en que se realizan la rotación y la reflexión no importa (es decir, estas operaciones se conmutan). La rotación impropia también se define como la composición de una rotación sobre un eje y una inversión sobre un punto del eje. Estas definiciones son equivalentes porque la inversión sobre un punto es equivalente a una rotación de 180° sobre cualquier eje, seguida de una simetría sobre un plano perpendicular a ese eje. Los elementos de simetría para una rotación impropia son el eje de rotación y el plano de simetría, el punto de inversión o ambos. El grupo de rotación impropia de orden 2n se denota como S2n.
Inversión
Para la inversión, denotada como i, debe haber un punto en el centro de un objeto que sea el centro de inversión. La inversión consiste en pasar cada punto a través del centro de inversión y hacia afuera a la misma distancia en el otro lado de la molécula. En la operación de inversión para coordenadas 3D, el centro de inversión es el origen (0,0,0). Cuando se invierte un objeto, el vector de posición de un punto en un objeto, ⟨x,y,z⟩, se invierte a ⟨-x,-y,-z⟩.
Galería
- Ejemplo de plano de espejo vertical.
- molécula de ferroceno, un objeto S10 simetría. Sus elementos de simetría son: un eje de rotación vertical, un plano horizontal y un punto de inversión en el centro.
Véase también
- Simmetría
- Teoría del grupo
- Cristalografía
- Notación Hermann-Mauguin
- Schoenflies notation
Referencias
- ^ Robert G. Mortimer (10 de junio de 2005). Matemáticas para Química Física. Academic Press. pp. 276–. ISBN 978-0-08-049288-9.
- ^ a b "Elemento de simetría". Diccionario online de Crystallography. 2021-09-25. Retrieved 2021-09-25.
- ^ a b Wolff, P.M. de; et al. (1989). "Definición de elementos de simetría en grupos espaciales y grupos de puntos. Report of the International Union of Crystallography Ad-Hoc Committee on the Nomenclature of Symmetry". Acta Crystallographica Sección A. 45 (7): 494-499. doi:10.1107/S0108767389002230. ISSN 0108-7673. Retrieved 2021-09-29.
- ^ a b Burns, Gerald; Glazer, A.M. (2013). Space Groups for Solid State Scientists. Elsevier. doi:10.1016/c2011-0-05712-5. ISBN 978-0-12-394400-9.
- ^ Atkins, Peter (2006). CHEMISTRY PHYSICAL DE ATKINS. Publicado en Gran Bretaña por Oxford University Prensa: W.H. Freeman and Company. p. 405. ISBN 0-7167-8759-8.
- ^ Smart, Lesley (2005). Química de estado sólido: una introducción. Elaine Moore (3rd ed.). Boca Raton: CRC Prensa. ISBN 0-7487-7516-1 OCLC 56661923.

