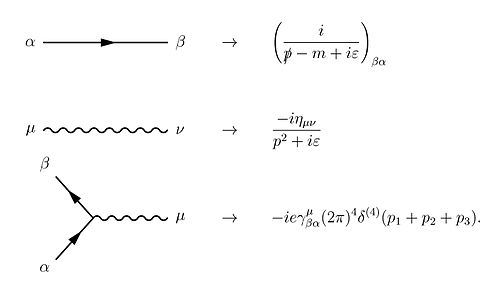Electrodinámica cuántica

ImprimirCitar

Teoría de campo cuántico del electromagnetismo

En física de partículas, la electrodinámica cuántica (QED) es la teoría relativista de campos cuánticos de la electrodinámica. En esencia, describe cómo interactúan la luz y la materia y es la primera teoría en la que se logra un acuerdo total entre la mecánica cuántica y la relatividad especial. QED describe matemáticamente todos los fenómenos que involucran partículas cargadas eléctricamente que interactúan mediante el intercambio de fotones y representa la contrapartida cuántica del electromagnetismo clásico dando cuenta completa de la interacción entre materia y luz.

En términos técnicos, QED se puede describir como una teoría de perturbación del vacío cuántico electromagnético. Richard Feynman lo llamó "la joya de la física" por sus predicciones extremadamente precisas de cantidades como el momento magnético anómalo del electrón y el cambio de Lamb de los niveles de energía del hidrógeno.

Historia

Paul Dirac

La primera formulación de una teoría cuántica que describe la interacción entre la radiación y la materia se atribuye al científico británico Paul Dirac, quien (durante la década de 1920) pudo calcular el coeficiente de emisión espontánea de un átomo.

Dirac describió la cuantización del campo electromagnético como un conjunto de osciladores armónicos con la introducción del concepto de operadores de creación y aniquilación de partículas. En los años siguientes, con las contribuciones de Wolfgang Pauli, Eugene Wigner, Pascual Jordan, Werner Heisenberg y una elegante formulación de la electrodinámica cuántica de Enrico Fermi, los físicos llegaron a creer que, en principio, sería posible realizar cualquier cálculo para cualquier condición física. Proceso que involucra fotones y partículas cargadas. Sin embargo, estudios posteriores de Felix Bloch con Arnold Nordsieck y Victor Weisskopf, en 1937 y 1939, revelaron que tales cálculos eran confiables solo en un primer orden de la teoría de la perturbación, un problema ya señalado por Robert Oppenheimer. En los órdenes superiores de la serie surgieron infinitos, lo que hizo que tales cálculos no tuvieran sentido y arrojó serias dudas sobre la consistencia interna de la teoría misma. Sin una solución conocida para este problema en ese momento, parecía que existía una incompatibilidad fundamental entre la relatividad especial y la mecánica cuántica.

Hans Bethe

Las dificultades con la teoría aumentaron a finales de la década de 1940. Las mejoras en la tecnología de microondas hicieron posible tomar medidas más precisas del cambio de los niveles de un átomo de hidrógeno, ahora conocido como el cambio Lamb y el momento magnético del electrón. Estos experimentos expusieron discrepancias que la teoría no pudo explicar.

Hans Bethe dio un primer indicio de una posible salida en 1947, después de asistir a la Conferencia de Shelter Island. Mientras viajaba en tren desde la conferencia a Schenectady, hizo el primer cálculo no relativista del desplazamiento de las líneas del átomo de hidrógeno medido por Lamb y Retherford. A pesar de las limitaciones del cálculo, la concordancia fue excelente. La idea era simplemente asignar infinitos a las correcciones de masa y carga que en realidad se fijaron en un valor finito mediante experimentos. De esta manera, los infinitos se absorben en esas constantes y dan un resultado finito en buena concordancia con los experimentos. Este procedimiento se denominó renormalización.

Feynman (centro) y Oppenheimer (derecha) en Los Álamos.

Según la intuición de Bethe y los artículos fundamentales sobre el tema de Shin'ichirō Tomonaga, Julian Schwinger, Richard Feynman y Freeman Dyson, finalmente fue posible obtener formulaciones completamente covariantes que fueran finitas en cualquier orden en una serie de perturbaciones de la electrodinámica cuántica. Shin'ichirō Tomonaga, Julian Schwinger y Richard Feynman fueron galardonados conjuntamente con el Premio Nobel de Física de 1965 por su trabajo en esta área. Sus contribuciones, y las de Freeman Dyson, fueron sobre formulaciones covariantes e invariantes de calibre de la electrodinámica cuántica que permiten cálculos de observables en cualquier orden de la teoría de la perturbación. La técnica matemática de Feynman, basada en sus diagramas, inicialmente parecía muy diferente del enfoque de la teoría de campos y basado en operadores de Schwinger y Tomonaga, pero Freeman Dyson demostró más tarde que los dos enfoques eran equivalentes. La renormalización, la necesidad de dar un significado físico a ciertas divergencias que aparecen en la teoría a través de integrales, se ha convertido posteriormente en uno de los aspectos fundamentales de la teoría cuántica de campos y se ha llegado a considerar como un criterio para la aceptabilidad general de una teoría. Aunque la renormalización funciona muy bien en la práctica, Feynman nunca se sintió del todo cómodo con su validez matemática, e incluso se refirió a la renormalización como un 'juego de trileros'. y "abracadabra".

QED ha servido como modelo y plantilla para todas las teorías cuánticas de campos posteriores. Una de esas teorías posteriores es la cromodinámica cuántica, que comenzó a principios de la década de 1960 y alcanzó su forma actual en el trabajo de la década de 1970 de H. David Politzer, Sidney Coleman, David Gross y Frank Wilczek. Sobre la base del trabajo pionero de Schwinger, Gerald Guralnik, Dick Hagen y Tom Kibble, Peter Higgs, Jeffrey Goldstone y otros, Sheldon Glashow, Steven Weinberg y Abdus Salam demostraron de forma independiente cómo la fuerza nuclear débil y la electrodinámica cuántica podrían fusionarse en un fuerza electrodébil única.

La visión de Feynman de la electrodinámica cuántica

Introducción

Cerca del final de su vida, Richard Feynman dio una serie de conferencias sobre QED destinadas al público general. Estas conferencias fueron transcritas y publicadas como Feynman (1985), QED: The Strange Theory of Light and Matter, una exposición clásica no matemática de QED desde el punto de vista articulado a continuación.

Los componentes clave de la presentación de QED de Feynman son tres acciones básicas.

Un fotón va de un lugar y tiempo a otro lugar y tiempo.

Un electrón va de un lugar y tiempo a otro lugar y tiempo.

Un electrón emite o absorbe un fotón en un determinado lugar y tiempo.

Elementos del diagrama Feynman

Estas acciones están representadas en forma de taquigrafía visual por los tres elementos básicos de los diagramas de Feynman: una línea ondulada para el fotón, una línea recta para el electrón y una unión de dos líneas rectas y una ondulada para un vértice que representa emisión o absorción de un fotón por un electrón. Todo esto se puede ver en el diagrama adyacente.

Además del cortocircuito visual para las acciones, Feynman presenta otro tipo de cortocircuito para las cantidades numéricas llamadas amplitudes de probabilidad. La probabilidad es el cuadrado del valor absoluto de la amplitud total de probabilidad, ${displaystyle {text{probability}}=|f({text{amplitude}})|^{2}}$ . Si un fotono se mueve de un lugar y tiempo $A$ a otro lugar y tiempo $B$ , la cantidad asociada está escrita en el cortocircuito de Feynman ${displaystyle P(A{text{ to }}B)}$ , y depende sólo del impulso y la polarización del fotón. La cantidad similar para un electrón que se mueve de $C$ a $D$ escrito ${displaystyle E(C{text{ to }}D)}$ . Depende del impulso y polarización del electrón, además de una constante llamada de Feynman n, a veces llamada la masa "bara" del electrón: está relacionada con, pero no igual que, la masa de electrones medidos. Finalmente, la cantidad que nos habla de la amplitud de probabilidad de un electrón para emitir o absorber un fotono llamado Feynman j, y a veces se llama la carga "bare" del electrón: es una constante, y está relacionado con, pero no el mismo que, la carga de electrones medidos e.

QED se basa en la suposición de que las interacciones complejas de muchos electrones y fotones se pueden representar reuniendo una colección adecuada de los tres bloques de construcción anteriores y luego usando las amplitudes de probabilidad para calcular la probabilidad de cualquier interacción tan compleja. Resulta que la idea básica de QED se puede comunicar suponiendo que el cuadrado del total de las amplitudes de probabilidad mencionadas anteriormente (P(A a B), E(C a D) y j) actúa como nuestra probabilidad diaria (a simplificación realizada en el libro de Feynman). Más adelante, esto se corregirá para incluir específicamente matemáticas de estilo cuántico, siguiendo a Feynman.

Las reglas básicas de amplitudes de probabilidad que se utilizarán son:

Si un evento puede ocurrir a través de varios indistinguible procesos alternativos (a.k.a. procesos "virtuales", entonces su amplitud de probabilidad es la suma de las amplitudes de probabilidad de las alternativas.
Si un proceso (virtual) implica una serie de subprocesos independientes, entonces su amplitud de probabilidad es la producto de las amplitudes de probabilidad del componente.

Construcciones básicas

Supongamos que comenzamos con un electrón en un lugar y tiempo determinados (a este lugar y tiempo se les asigna la etiqueta arbitraria A) y un fotón en otro lugar y tiempo (asignan la etiqueta B ). Una pregunta típica desde un punto de vista físico es: "¿Cuál es la probabilidad de encontrar un electrón en C (otro lugar y un tiempo posterior) y un fotón en D? (otro lugar y tiempo más)?". El proceso más simple para lograr este fin es que el electrón se mueva de A a C (una acción elemental) y que el fotón se mueva de B a D (otra acción elemental). A partir del conocimiento de las amplitudes de probabilidad de cada uno de estos subprocesos: E(A a C) y P(B a D): esperaríamos calcular la amplitud de probabilidad de que ambos sucedan juntos multiplicándolos, usando la regla b) anterior. Esto da una amplitud de probabilidad general estimada simple, que se eleva al cuadrado para dar una probabilidad estimada.

Dispersión compton

Pero hay otras formas en las que podría producirse el resultado final. El electrón podría moverse a un lugar y tiempo E, donde absorbe el fotón; luego sigue adelante antes de emitir otro fotón en F; luego pasa a C, donde se detecta, mientras que el nuevo fotón pasa a D. La probabilidad de este proceso complejo se puede calcular nuevamente conociendo las amplitudes de probabilidad de cada una de las acciones individuales: tres acciones de electrones, dos acciones de fotones y dos vértices: una emisión y una absorción. Esperaríamos encontrar la amplitud de probabilidad total multiplicando las amplitudes de probabilidad de cada una de las acciones, para cualquier posición elegida de E y F. Luego, usando la regla a) anterior, tenemos que sumar todas estas amplitudes de probabilidad para todas las alternativas para E y F. (Esto no es elemental en la práctica e implica integración). Pero existe otra posibilidad, que es que el electrón primero se mueva a G, donde emite un fotón, que pasa a D, mientras que el electrón pasa a H, donde absorbe el primer fotón, antes de pasar a C. Nuevamente, podemos calcular la amplitud de probabilidad de estas posibilidades (para todos los puntos G y H). Entonces tenemos una mejor estimación de la amplitud de probabilidad total al sumar las amplitudes de probabilidad de estas dos posibilidades a nuestra estimación simple original. Por cierto, el nombre dado a este proceso de interacción de un fotón con un electrón es dispersión Compton.

Hay un número infinito de otros intermediarios "virtuales" procesos en los que cada vez se absorben y/o emiten más fotones. Para cada uno de estos procesos, se podría dibujar un diagrama de Feynman que lo describa. Esto implica un cálculo complejo para las amplitudes de probabilidad resultantes, pero dado el caso de que cuanto más complicado sea el diagrama, menos contribuirá al resultado, es solo cuestión de tiempo y esfuerzo encontrar una respuesta tan precisa como uno desee. a la pregunta original. Este es el enfoque básico de QED. Para calcular la probabilidad de cualquier proceso interactivo entre electrones y fotones, es cuestión de observar primero, con diagramas de Feynman, todas las formas posibles en las que el proceso puede construirse a partir de los tres elementos básicos. Cada diagrama involucra algún cálculo que involucra reglas definidas para encontrar la amplitud de probabilidad asociada.

Ese andamiaje básico permanece cuando uno pasa a una descripción cuántica, pero se necesitan algunos cambios conceptuales. Una es que, si bien podríamos esperar en nuestra vida cotidiana que habría algunas restricciones en los puntos a los que se puede mover una partícula, eso no es cierto en la electrodinámica cuántica completa. Hay una amplitud de probabilidad distinta de cero de un electrón en A, o un fotón en B, moviéndose como una acción básica a cualquier otro lugar y tiempo en el universo. Eso incluye lugares a los que solo se podía llegar a velocidades superiores a la de la luz y también tiempos anteriores. (Un electrón que retrocede en el tiempo puede verse como un positrón que avanza en el tiempo).

Amplitudes de probabilidad

Feynman reemplaza números complejos con flechas giratorias, que comienzan a la emisión y terminan al detectar una partícula. La suma de todas las flechas resultantes da una flecha final cuya longitud cuadrada equivale a la probabilidad del evento. En este diagrama, luz emitida por la fuente S puede llegar al detector P rebotando el espejo (en azul) en varios puntos. Cada uno de los caminos tiene una flecha asociada con ella (cuya dirección cambia uniformemente con la tiempo tomada para la luz para atravesar el camino). Para calcular correctamente la probabilidad total de que la luz alcance P empezando S, uno necesita resumir las flechas para Todos tales caminos. El gráfico que figura a continuación muestra el tiempo total dedicado a atravesar cada uno de los caminos anteriores.

La mecánica cuántica introduce un cambio importante en la forma en que se calculan las probabilidades. Las probabilidades todavía están representadas por los números reales habituales que usamos para las probabilidades en nuestro mundo cotidiano, pero las probabilidades se calculan como el módulo cuadrado de las amplitudes de probabilidad, que son números complejos.

Feynman evita exponer al lector a las matemáticas de los números complejos al usar una representación simple pero precisa de ellos como flechas en una hoja de papel o una pantalla. (Estos no deben confundirse con las flechas de los diagramas de Feynman, que son representaciones simplificadas en dos dimensiones de una relación entre puntos en tres dimensiones del espacio y una del tiempo). Las flechas de amplitud son fundamentales para la descripción del mundo dada por cuántica. teoría. Están relacionados con nuestras ideas cotidianas de probabilidad por la regla simple de que la probabilidad de un evento es el cuadrado de la longitud de la flecha de amplitud correspondiente. Entonces, para un proceso dado, si están involucradas dos amplitudes de probabilidad, v y w, la probabilidad del proceso estará dada por

{displaystyle P=|mathbf {v} +mathbf {w} |^{2}}

{displaystyle P=|mathbf {v} ,mathbf {w} |^{2}.}

Sin embargo, las reglas con respecto a sumar o multiplicar son las mismas que las anteriores. Pero donde esperaría sumar o multiplicar probabilidades, en su lugar suma o multiplica amplitudes de probabilidad que ahora son números complejos.

Adición de amplitudes de probabilidad como números complejos

Multiplicación de amplitudes de probabilidad como números complejos

La suma y la multiplicación son operaciones comunes en la teoría de los números complejos y se dan en las figuras. La suma se encuentra de la siguiente manera. Deje que el comienzo de la segunda flecha esté al final de la primera. La suma es entonces una tercera flecha que va directamente desde el principio de la primera hasta el final de la segunda. El producto de dos flechas es una flecha cuya longitud es el producto de las dos longitudes. La dirección del producto se encuentra sumando los ángulos que cada uno de los dos ha girado con respecto a una dirección de referencia: eso da el ángulo con el que gira el producto con respecto a la dirección de referencia.

Ese cambio, de probabilidades a amplitudes de probabilidad, complica las matemáticas sin cambiar el enfoque básico. Pero ese cambio todavía no es suficiente porque no tiene en cuenta el hecho de que tanto los fotones como los electrones pueden polarizarse, es decir, hay que tener en cuenta sus orientaciones en el espacio y el tiempo. Por lo tanto, P(A a B) consta de 16 números complejos o flechas de amplitud de probabilidad. También hay algunos cambios menores que tienen que ver con la cantidad j, que puede tener que rotarse en un múltiplo de 90° para algunas polarizaciones, lo que solo es de interés para la contabilidad detallada.

Asociado con el hecho de que el electrón se puede polarizar hay otro pequeño detalle necesario, que está relacionado con el hecho de que un electrón es un fermión y obedece a las estadísticas de Fermi-Dirac. La regla básica es que si tenemos la amplitud de probabilidad para un proceso complejo dado que involucra más de un electrón, entonces cuando incluimos (como siempre debemos) el diagrama de Feynman complementario en el que intercambiamos dos eventos de electrones, la amplitud resultante es la inversa. – el negativo – del primero. El caso más simple sería dos electrones comenzando en A y B terminando en C y D. La amplitud se calcularía como la "diferencia", E(A a D) × E(B a C) − E(A a C) × E(B a D), donde esperaríamos, según nuestra idea cotidiana de probabilidades, que sería una suma.

Propagadores

Finalmente, uno tiene que calcular P(A a B) y E(C a D) correspondientes a las amplitudes de probabilidad para el fotón y el electrón respectivamente. Estas son esencialmente las soluciones de la ecuación de Dirac, que describen el comportamiento de la amplitud de probabilidad del electrón y las ecuaciones de Maxwell, que describen el comportamiento de la amplitud de probabilidad del fotón. Estos se llaman propagadores de Feynman. La traducción a una notación comúnmente utilizada en la literatura estándar es la siguiente:

{displaystyle P(A{text{ to }}B)to D_{F}(x_{B}-x_{A}),quad E(C{text{ to }}D)to S_{F}(x_{D}-x_{C}),}

donde un símbolo corto como $x_{A}$ representa los cuatro números reales que dan el tiempo y la posición en tres dimensiones del punto etiquetado A.

Renormalización masiva

Loop electron autoenergía

Históricamente surgió un problema que detuvo el progreso durante veinte años: aunque partimos del supuesto de tres "simples" acciones, las reglas del juego dicen que si queremos calcular la amplitud de probabilidad de que un electrón pase de A a B, debemos tener en cuenta todas las formas posibles: todos los diagramas de Feynman posibles con esos puntos finales. Por lo tanto, habrá una forma en que el electrón viaje a C, emita un fotón allí y luego lo absorba nuevamente en D antes de pasar a B. O podría hacer este tipo de cosas dos veces, o más. En resumen, tenemos una situación similar a un fractal en la que si miramos de cerca una línea, se divide en una colección de "simples" líneas, cada una de las cuales, si se mira de cerca, se compone a su vez de "simple" líneas, y así sucesivamente ad infinitum. Esta es una situación difícil de manejar. Si agregar ese detalle solo alteró las cosas ligeramente, entonces no habría sido tan malo, pero ocurrió un desastre cuando se descubrió que la simple corrección mencionada anteriormente conducía a amplitudes de probabilidad infinitas. Con el tiempo, este problema se "solucionó" por la técnica de la renormalización. Sin embargo, el propio Feynman se mostró descontento al respecto, calificándolo de "proceso dippy".

Conclusiones

Dentro del marco anterior, los físicos pudieron calcular con un alto grado de precisión algunas de las propiedades de los electrones, como el momento dipolar magnético anómalo. Sin embargo, como señala Feynman, no logra explicar por qué las partículas como el electrón tienen las masas que tienen. "No existe una teoría que explique adecuadamente estos números. Usamos los números en todas nuestras teorías, pero no los entendemos, qué son o de dónde vienen. Creo que desde un punto de vista fundamental, este es un problema muy interesante y serio."

Formulación matemática

Acción QED

Matemáticamente, QED es una teoría de norma abeliana con el grupo de simetría U(1), definido en el espacio de Minkowski (espacio-tiempo plano). El campo de calibre, que media la interacción entre los campos de espín-1/2 cargados, es el campo electromagnético. El lagrangiano QED para un campo de espín-1/2 que interactúa con el campo electromagnético en unidades naturales da lugar a la acción

QED Medida

${displaystyle S_{text{QED}}=int d^{4}x,left[-{frac {1}{4}}F^{mu nu }F_{mu nu }+{bar {psi }},(igamma ^{mu }D_{mu }-m),psi right]}$

dónde

$gamma ^{mu }$ Son matrices Dirac.
$psi$ a bispinor campo de partículas spin-1/2 (por ejemplo, electron-positron campo).
${bar {psi }}equiv psi ^{dagger }gamma ^{0}$ , llamado "psi-bar", a veces se conoce como el adjoint Dirac.
Dμ μ ↑ ↑ ∂ ∂ μ μ +ieAμ μ +ieBμ μ {displaystyle D_{mu }equiv partial ################################################################################################################################################################################################################################################################ }+ieA_{mu }+ieB_{mu } ${displaystyle D_{mu }equiv partial _{mu }+ieA_{mu }+ieB_{mu }}$ es el derivado covariante de calibre.
- e es la constante de acoplamiento, igual a la carga eléctrica del campo bispinor.
- $A_{mu }$ es el covariante cuatro-potencial del campo electromagnético generado por el electron mismo. También se conoce como un campo de calibre o un ${displaystyle {text{U}}(1)}$ conexión.
- $B_{mu }$ es el campo externo impuesto por fuente externa.
m es la masa del electrón o positrón.
${displaystyle F_{mu nu }=partial _{mu }A_{nu }-partial _{nu }A_{mu }}$ es el tensor de campo electromagnético. Esto también se conoce como la curvatura del campo de calibre.

Ampliar el derivado covariante revela una segunda forma útil del Lagrangiano (campo externo) $B_{mu }$ fijado a cero para la simplicidad)

{displaystyle {mathcal {L}}=-{frac {1}{4}}F_{mu nu }F^{mu nu }+{bar {psi }}(igamma ^{mu }partial _{mu }-m)psi -ej^{mu }A_{mu }}

Donde $j^{mu }$ es el conservado ${displaystyle {text{U}}(1)}$ corriente que surge del teorema de Noether. Está escrito

{displaystyle j^{mu }={bar {psi }}gamma ^{mu }psi.}

Ecuaciones de movimiento

Expandir la derivada covariante en el Lagrangiano da

{displaystyle {mathcal {L}}=-{frac {1}{4}}F_{mu nu }F^{mu nu }+i{bar {psi }}gamma ^{mu }partial _{mu }psi -e{bar {psi }}gamma ^{mu }A_{mu }psi -m{bar {psi }}psi }

{displaystyle =-{frac {1}{4}}F_{mu nu }F^{mu nu }+i{bar {psi }}gamma ^{mu }partial _{mu }psi -m{bar {psi }}psi -ej^{mu }A_{mu }.}

Para la simplicidad, $B_{mu }$ ha sido fijado a cero. Alternativamente, podemos absorber $B_{mu }$ en un nuevo campo de calibre ${displaystyle A'_{mu }=A_{mu }+B_{mu }}$ y reetiquetar el nuevo campo como ${displaystyle A_{mu }.}$

De este Lagrangiano, las ecuaciones de movimiento para el $psi$ y $A_{mu }$ se pueden obtener campos.

Ecuación de movimiento para ψ

Estos surgen más directamente considerando la ecuación Euler-Lagrange para ${displaystyle {bar {psi }}}$ . Desde el Lagrangiano no contiene ${displaystyle partial _{mu }{bar {psi }}}$ términos, inmediatamente recibimos

{displaystyle {frac {partial {mathcal {L}}}{partial {bar {psi }}}}=0}

así la ecuación del movimiento puede ser escrita ${displaystyle (igamma ^{mu }partial _{mu }-m)psi =egamma ^{mu }A_{mu }psi.}$

Ecuación de movimiento para Aμ

Usando la ecuación Euler-Lagrange para la $A_{mu }$ campo,

{displaystyle partial _{nu }left({frac {partial {mathcal {L}}}{partial (partial _{nu }A_{mu })}}right)-{frac {partial {mathcal {L}}}{partial A_{mu }}}=0,}

()3)

las derivadas esta vez son

{displaystyle partial _{nu }left({frac {partial {mathcal {L}}}{partial (partial _{nu }A_{mu })}}right)=partial _{nu }left(partial ^{mu }A^{nu }-partial ^{nu }A^{mu }right),}

{displaystyle {frac {partial {mathcal {L}}}{partial A_{mu }}}=-e{bar {psi }}gamma ^{mu }psi.}

Reemplazar en (3) conduce a

{displaystyle partial _{mu }F^{mu nu }=e{bar {psi }}gamma ^{nu }psi }

que se puede escribir en términos de ${displaystyle {text{U}}(1)}$ corriente $j^{mu }$ como

${displaystyle partial _{mu }F^{mu nu }=ej^{nu }.}$

Ahora, si imponemos la condición de calibre de Lorenz

{displaystyle partial _{mu }A^{mu }=0,}

{displaystyle Box A^{mu }=ej^{mu },}

{displaystyle Box =partial _{mu }partial ^{mu }}

Imagen de interacción

Esta teoría puede cuantificarse directamente al tratar los sectores bosónicos y fermiónicos como libres. Esto nos permite construir un conjunto de estados asintomáticos que se pueden utilizar para comenzar la computación de las amplitudes de probabilidad para diferentes procesos. Para ello, tenemos que calcular un operador de evolución, que para un estado inicial dado $|irangle$ dará un estado final $langle f|$ de tal manera

{displaystyle M_{fi}=langle f|U|irangle.}

Esta técnica también se conoce como matriz S. El operador de evolución se obtiene en la imagen de interacción, donde la evolución temporal viene dada por la interacción hamiltoniana, que es la integral sobre el espacio del segundo término en la densidad lagrangiana dada anteriormente:

{displaystyle V=eint d^{3}x,{bar {psi }}gamma ^{mu }psi A_{mu },}

y así, uno tiene

{displaystyle U=Texp left[-{frac {i}{hbar }}int _{t_{0}}^{t}dt',V(t')right],}

donde T es el operador de ordenación temporal. Este operador de evolución solo tiene significado como una serie, y lo que obtenemos aquí es una serie de perturbaciones con la constante de estructura fina como parámetro de desarrollo. Esta serie se llama la serie Dyson.

Diagramas de Feynman

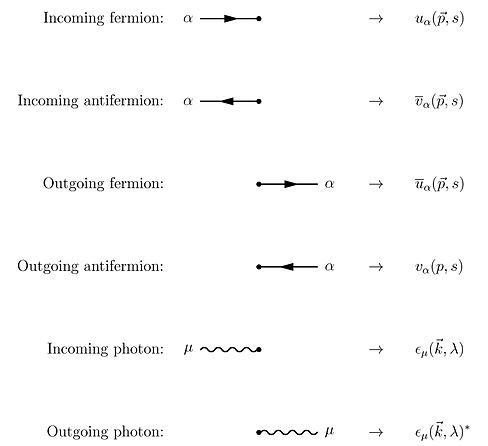
A pesar de la claridad conceptual de este enfoque de Feynman para QED, casi ninguno de los primeros libros de texto lo sigue en su presentación. Al realizar cálculos, es mucho más fácil trabajar con las transformadas de Fourier de los propagadores. Las pruebas experimentales de electrodinámica cuántica suelen ser experimentos de dispersión. En la teoría de la dispersión, las partículas' se consideran los momentos en lugar de sus posiciones, y es conveniente pensar en las partículas como creadas o aniquiladas cuando interactúan. Los diagramas de Feynman entonces parecen iguales, pero las líneas tienen diferentes interpretaciones. La línea de electrones representa un electrón con una energía y un momento determinados, con una interpretación similar de la línea de fotones. Un diagrama de vértices representa la aniquilación de un electrón y la creación de otro junto con la absorción o creación de un fotón, cada uno con energías y momentos específicos.

Usando el teorema de Wick sobre los términos de la serie de Dyson, todos los términos de la matriz S para la electrodinámica cuántica se pueden calcular mediante la técnica de los diagramas de Feynman. En este caso, las reglas para dibujar son las siguientes

A estas reglas debemos añadir otra para bucles cerrados que implica una integración en momenta ${textstyle int d^{4}p/(2pi)^{4}}$ , ya que estas partículas internas ("virtuales") no se limitan a ningún tipo de energía-momento específico, incluso que generalmente se requiere por relatividad especial (ver Propagator para detalles). La firma de la métrica ${displaystyle eta _{mu nu }}$ es ${displaystyle {rm {diag}}(+---)}$ .

De ellos, los cálculos de amplitudes de probabilidad se dan directamente. Un ejemplo es la dispersión de Compton, con un electrón y un fotón experimentando una dispersión elástica. Los diagramas de Feynman son en este caso

y así podemos obtener la amplitud correspondiente en el primer orden de una serie de perturbaciones para la matriz S:

{displaystyle M_{fi}=(ie)^{2}{overline {u}}({vec {p}}',s')epsilon !!!/,'({vec {k}}',lambda ')^{*}{frac {p!!!/+k!!!/+m_{e}}{(p+k)^{2}-m_{e}^{2}}}epsilon !!!/({vec {k}},lambda)u({vec {p}},s)+(ie)^{2}{overline {u}}({vec {p}}',s')epsilon !!!/({vec {k}},lambda){frac {p!!!/-k!!!/'+m_{e}}{(p-k')^{2}-m_{e}^{2}}}epsilon !!!/,'({vec {k}}',lambda ')^{*}u({vec {p}},s),}

a partir de la cual podemos calcular la sección transversal de esta dispersión.

Fenómenos no perturbativos

El éxito predictivo de la electrodinámica cuántica se basa en gran medida en el uso de la teoría de perturbaciones, expresada en los diagramas de Feynman. Sin embargo, la electrodinámica cuántica también conduce a predicciones más allá de la teoría de perturbaciones. En presencia de campos eléctricos muy fuertes, predice que se producirán espontáneamente electrones y positrones, lo que provocará la descomposición del campo. Este proceso, llamado efecto Schwinger, no puede entenderse en términos de un número finito de diagramas de Feynman y, por lo tanto, se describe como no perturbativo. Matemáticamente, se puede derivar mediante una aproximación semiclásica a la integral de trayectoria de la electrodinámica cuántica.

Renormalizabilidad

Los términos de orden superior se pueden calcular directamente para el operador de evolución, pero estos términos muestran diagramas que contienen los siguientes más simples

Contribución única a la función de polarización de vacío $Pi$
Contribución de un solo bucle a la función de energía de electrones $Sigma$
Una contribución a la función del vértice $Gamma$

que, al ser lazos cerrados, implican la presencia de integrales divergentes que no tienen significado matemático. Para superar esta dificultad, se ha ideado una técnica llamada renormalización, que produce resultados finitos muy de acuerdo con los experimentos. Un criterio para que la teoría sea significativa después de la renormalización es que el número de diagramas divergentes sea finito. En este caso, se dice que la teoría es "renormalizable". La razón de esto es que para volver a normalizar los observables, se necesita un número finito de constantes para mantener intacto el valor predictivo de la teoría. Este es exactamente el caso de la electrodinámica cuántica que muestra solo tres diagramas divergentes. Este procedimiento da observables en muy estrecha concordancia con el experimento como se ve, p. para la relación giromagnética de electrones.

La renormalizabilidad se ha convertido en un criterio esencial para que una teoría cuántica de campos se considere viable. Todas las teorías que describen las interacciones fundamentales, excepto la gravitación, cuya contrapartida cuántica es sólo una conjetura y actualmente se encuentra bajo una investigación muy activa, son teorías renormalizables.

No convergencia de series

Un argumento de Freeman Dyson muestra que el radio de convergencia de la serie de perturbaciones en QED es cero. El argumento básico es el siguiente: si la constante de acoplamiento fuera negativa, esto sería equivalente a que la constante de fuerza de Coulomb fuera negativa. Esto sería "inverso" la interacción electromagnética de modo que las cargas similares se atraigan y las cargas diferentes se rechacen. Esto haría que el vacío fuera inestable frente a la descomposición en un grupo de electrones en un lado del universo y un grupo de positrones en el otro lado del universo. Porque la teoría es "enferma" para cualquier valor negativo de la constante de acoplamiento, la serie no converge sino que, en el mejor de los casos, es una serie asintótica.

Desde una perspectiva moderna, decimos que la QED no está bien definida como una teoría cuántica de campos para energías arbitrariamente altas. La constante de acoplamiento se extiende hasta el infinito con energía finita, lo que indica un polo de Landau. El problema es esencialmente que QED parece sufrir problemas de trivialidad cuántica. Esta es una de las motivaciones para incorporar QED dentro de una Gran Teoría Unificada.

Electrodinámica en el espacio-tiempo curvo

Esta teoría se puede extender, al menos como una teoría de campo clásica, al espacio-tiempo curvo. Esto surge de manera similar al caso del espacio-tiempo plano, al acoplar una teoría electromagnética libre a una teoría del fermión libre e incluir una interacción que promueve la derivada parcial en la teoría del fermión a una derivada covariante de norma.

Contenido relacionado

Más resultados...