El problema de la señora Miniver

Tres casos del problema de la Sra. Miniver. En cada caso el área amarilla interior iguala el área total de las regiones azules circundantes. El caso izquierdo muestra dos círculos de áreas iguales, el caso derecho muestra un círculo con el doble del área del otro, y el caso intermedio es intermedio entre estos dos.

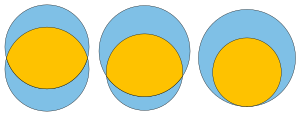
Problema de la Sra. Miniver es un problema de geometría sobre el área de los círculos. Pregunta cómo colocar dos círculos A{displaystyle A} y B{displaystyle B} de radio dado de tal manera que la lente formada por la intersección de sus dos interiores tiene igual área a la diferencia simétrica de A{displaystyle A} y B{displaystyle B} (la zona contenida en uno pero no en ambos círculos). Fue nombrado por una analogía entre geometría y dinámicas sociales enunciadas por el personaje ficticio Sra. Miniver, quien "visó todas las relaciones como un par de círculos interseccionistas". Su solución implica una ecuación trascendental.

Origen

El problema se deriva de "A Country House Visit", uno de los artículos periodísticos de Jan Struther que apareció en el Times of London entre 1937 y 1939 y presenta a su personaje, la Sra..Miniver. Según la historia:

Vio todas las relaciones como un par de círculos intersectiendo. Parecería a primera vista que cuanto más superaban mejor la relación; pero esto no es así. Más allá de cierto punto, la ley de la disminución de los rendimientos establece, y no hay suficientes recursos privados de ambos lados para enriquecer la vida que se comparte. Probablemente la perfección se alcanza cuando el área de las dos crescentes exteriores, agregadas juntas, es exactamente igual a la de la pieza en forma de hoja en el centro. En papel debe haber una fórmula matemática limpia para llegar a esto; en la vida, ninguna.

Louis A. Graham y Clifton Fadiman formalizaron las matemáticas del problema y las popularizaron entre los matemáticos recreativos.

Solución

El problema se puede resolver cortando la luna a lo largo del segmento de línea entre los dos puntos de cruce de los círculos, en dos segmentos circulares, y utilizando la fórmula para el área de un segmento circular para relacionar la distancia entre los puntos de cruce a la zona total que el problema requiere la lune para tener. Esto da una ecuación trascendental para la distancia entre los puntos de cruce pero se puede resolver numéricamente. Hay dos condiciones límite cuyas distancias entre los centros pueden ser resueltas fácilmente: la distancia más lejana que pueden ser los centros es cuando los círculos tienen radios iguales, y lo más cercano que pueden ser es cuando un círculo está contenido completamente dentro del otro, que sucede cuando la relación entre radios es 2{displaystyle {sqrt {2}}. Si la relación de radio cae más allá de estos casos limitantes, los círculos no pueden satisfacer la limitación del área del problema.

En el caso de dos círculos de igual tamaño, estas ecuaciones se pueden simplificar algo. El rhombus formado por los dos centros de círculo y los dos puntos de cruce, con longitudes laterales iguales al radio, tiene un ángulo Silencio Silencio .. 2.605{displaystyle theta approx 2.605} radians en los centros del círculo, encontrado por resolver la ecuación

Silencio Silencio − − pecado⁡ ⁡ Silencio Silencio =2π π 3,{displaystyle theta -sin theta ¿Qué?

2#⁡ ⁡ Silencio Silencio 2.. 0,529864{displaystyle 2cos {tfrac {theta } {2}approx 0.529864}