El método de Heun

En matemáticas y ciencias computacionales, el método de Heun puede referirse al método de Euler mejorado o modificado (es decir, la regla trapezoidal explícita), o a un método Runge-Kutta de dos etapas similar. Recibe su nombre en honor a Karl Heun y es un procedimiento numérico para resolver ecuaciones diferenciales ordinarias (EDO) con un valor inicial dado. Ambas variantes pueden considerarse extensiones del método de Euler en métodos Runge-Kutta de segundo orden de dos etapas.

El procedimiento para calcular la solución numérica del problema de valor inicial:

${\displaystyle y'(t)=f(t,y(t)),\qquad \qquad y(t_{0}=y_{0},}$

a través del método de Heun, es calcular primero el valor intermedio ${\displaystyle {\tilde {y}_{i+1}$ y luego la aproximación final ${\displaystyle Y...$ en el próximo punto de integración.

${\displaystyle {\fnMicrosoft} {y}_{i+1}=y_{i}+hf(t_{i},y_{i}}}$

${\displaystyle Y... {h}{2} {f(t_{i},y_{i})+f(t_{i+1},{\tilde {y}_{i+1})}}}$

Donde ${\displaystyle h}$ es el tamaño del paso y ${\displaystyle t_{i+1}=t_{i}+h}$.

El método de Euler se utiliza como base para el método de Heun. El método de Euler utiliza la línea tangente a la función al comienzo del intervalo como una estimación de la pendiente de la función en el intervalo, suponiendo que si el tamaño del paso es pequeño, el error será pequeño. Sin embargo, incluso cuando se utilizan tamaños de paso extremadamente pequeños, a lo largo de una gran cantidad de pasos el error comienza a acumularse y la estimación diverge del valor funcional real.

Cuando la curva solución es cóncava hacia arriba, su línea tangente subestimará la coordenada vertical del siguiente punto y viceversa para una solución cóncava hacia abajo. La línea de predicción ideal tocaría la curva en su siguiente punto predicho. En realidad, no hay forma de saber si la solución es cóncava hacia arriba o hacia abajo y, por lo tanto, si el siguiente punto predicho sobrestimará o subestimará su valor vertical. Tampoco se puede garantizar que la concavidad de la curva permanezca constante y la predicción puede sobreestimar y subestimar en diferentes puntos en el dominio de la solución. El método de Heun aborda este problema al considerar el intervalo abarcado por el segmento de la línea tangente como un todo. Tomando un ejemplo cóncavo hacia arriba, la línea de predicción de la tangente izquierda subestima la pendiente de la curva para todo el ancho del intervalo desde el punto actual hasta el siguiente punto predicho. Si se considera la línea tangente en el punto final derecho (que se puede estimar utilizando el método de Euler), tiene el problema opuesto. Los puntos a lo largo de la línea tangente del extremo izquierdo tienen coordenadas verticales que subestiman todas las que se encuentran en la curva solución, incluido el extremo derecho del intervalo en consideración. La solución es hacer que la pendiente sea mayor en cierta cantidad. El método de Heun considera las líneas tangentes a la curva solución en ambos extremos del intervalo, una que sobreestima y otra que subestima las coordenadas verticales ideales. Se debe construir una línea de predicción basada únicamente en la pendiente de la tangente del extremo derecho, aproximada mediante el método de Euler. Si esta pendiente pasa por el extremo izquierdo del intervalo, el resultado es evidentemente demasiado pronunciado para ser utilizado como una línea de predicción ideal y sobreestima el punto ideal. Por lo tanto, el punto ideal se encuentra aproximadamente a mitad de camino entre la sobreestimación y la subestimación erróneas, el promedio de las dos pendientes.

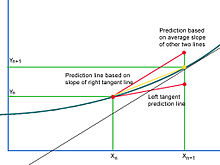
El Método de Euler se utiliza para calcular aproximadamente las coordenadas del siguiente punto en la solución, y con este conocimiento, la estimación original es re-predecida o corregido. Suponiendo que la cantidad ${\displaystyle \textstyle f(x,y)}$ en el lado derecho de la ecuación se puede considerar como la pendiente de la solución buscada en cualquier punto ${\displaystyle \textstyle (x,y)}$, esto se puede combinar con la estimación Euler del siguiente punto para dar la pendiente de la línea tangente en el punto final derecho. A continuación se utiliza el promedio de ambas pistas para encontrar las coordenadas corregidas del intervalo de extremo derecho.

${\displaystyle {\text{Slope}_{\text{left}=f(x_{i},y_{i}}}$

${\displaystyle {\text{Slope}_{\text{right}=f(x_{i}+h,y_{i}+hf(x_{i},y_{i}) }$

${\displaystyle {\text{Slope} {\text{ideal}={\frac} {1}{2} {\text{Slope} {\text{\left}}}}} {\text{\text{right}}}}}}} {\text{\text{right}}}}} {\f}}} {\f}} {\f}}}} {\f}}}} {\f}}} {\f}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$

Usando el principio de que la pendiente de una línea equivale a la altura o recorrido, las coordenadas al final del intervalo se pueden encontrar utilizando la siguiente fórmula:

${\displaystyle {\text{Slope} {\text{ideal}={\frac} {\Delta y} {h}}} {\fn}} {\fn}}}} {\fn}}}}}}}}} {\f}}}}}}}}}}}}}} {\Delta y} {} {} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}} {\Del}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\Delta}}}}}}}}}}}}}}}}}}} {\Del}}}}}}}}}}}}}}}}}}$

${\displaystyle \Delta y=h({\text{Slope}_{\text{ideal}}}}$

${\displaystyle x_{i+1}=x_{i}+h}$, ${\displaystyle \textstyle Y... Delta.$

${\displaystyle Y_{i+1}=y_{i}+h{\text{Slope} {\text{ideal}}$

${\displaystyle Y... {1}{2}h {\text{Slope}}_{\text{left}+{\text{Slope}}_{\text{right}}}}}} {\f}} {\f}}}} {\f}}}}} {\f}}} {\f} {\f}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

${\displaystyle Y_{i+1}=y_{i}+{\frac {h} {h}(f(x_{i},y_{i})+f(x_{i}+h,y_{i}+hf(x_{i},y_{i})) }$

La precisión del método Euler mejora sólo linealmente con el tamaño del paso se disminuye, mientras que el método Heun mejora la precisión cuadráticamente . El esquema se puede comparar con el método trapezoidal implícito, pero con ${\displaystyle f(t_{i+1},y_{i+1}) }$ sustituido por ${\displaystyle f(t_{i+1},{\tilde {y}_{i+1}}$ para hacerlo explícito. ${\displaystyle {\tilde {y}_{i+1}$ es el resultado de un paso del método de Euler en el mismo problema de valor inicial. Así que el método Heun es un método predictor-corrector con el método de Euler hacia adelante como método predictor y trapezoidal como corrector.

El método de Euler mejorado es un método de Runge-Kutta de dos etapas y se puede escribir utilizando la tabla de Butcher (según John C. Butcher):

El otro método, conocido como método de Heun (también conocido como método de Ralston), tiene el cuadro de Butcher:

Este método minimiza el error de truncamiento.