El método de Fisher

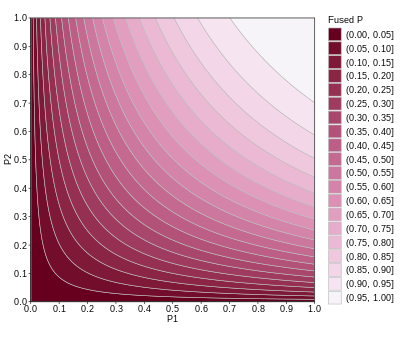
En estadística, el método de Fisher, también conocido como prueba de probabilidad combinada de Fisher, es una técnica de fusión de datos o "metaanálisis" (análisis de análisis). Fue desarrollado por Ronald Fisher y recibió su nombre en honor a él. En su forma básica, se utiliza para combinar los resultados de varias pruebas de independencia que se basan en la misma hipótesis general (H₀).

El método de Fisher combina las probabilidades de los valores extremos de cada prueba, comúnmente conocidos como "valores p", en una estadística de prueba (X²) utilizando la fórmula

${\displaystyle X_{2k} {2}=-2\sum ¿Qué? ¿Qué?$

donde p_i es el valor p para la i^ésima prueba de hipótesis. Cuando los valores p tienden a ser pequeños, el estadístico de prueba X² será grande, lo que sugiere que las hipótesis nulas no son verdaderas para cada prueba.

Cuando todas las hipótesis nulas son verdaderas y las p_i (o sus correspondientes estadísticas de prueba) son independientes, X² tiene una distribución de chi-cuadrado con 2k grados de libertad, donde k es el número de pruebas que se combinan. Este hecho se puede utilizar para determinar el valor p para X².

La distribución de X² es una distribución de chi-cuadrado por la siguiente razón: bajo la hipótesis nula para la prueba i, el valor p p_i sigue una distribución uniforme en el intervalo [0,1]. El logaritmo negativo de un valor distribuido uniformemente sigue una distribución exponencial. Al escalar un valor que sigue una distribución exponencial por un factor de dos, se obtiene una cantidad que sigue una distribución de chi-cuadrado con dos grados de libertad. Finalmente, la suma de k valores de chi-cuadrado independientes, cada uno con dos grados de libertad, sigue una distribución de chi-cuadrado con 2k grados de libertad.

La dependencia entre las pruebas estadísticas es generalmente positiva, lo que significa que p- valor de X² es demasiado pequeño (anticonservador) si no se tiene en cuenta la dependencia. Así, si el método de Fisher para pruebas independientes se aplica en un entorno dependiente, y el p- el valor no es lo suficientemente pequeño como para rechazar la hipótesis nula, entonces esa conclusión seguirá manteniendo incluso si la dependencia no se cuenta adecuadamente. Sin embargo, si no se cuenta la dependencia positiva y el metaanálisis p-el valor se encuentra pequeño, la evidencia contra la hipótesis nula es generalmente exagerada. El falso índice de descubrimiento, ${\displaystyle \alpha (k+1)/(2k)}$, ${\displaystyle \alpha }$ reducido para k prueba independiente o positivamente correlacionada, puede bastar para controlar alfa para una comparación útil a una sobre-pequeña p-valor de Fisher X².

En los casos en que las pruebas no son independientes, la distribución nula de X² es más complicada. Una estrategia común es aproximar la distribución nula con una variable aleatoria escalada de distribución χ2. Se pueden utilizar diferentes enfoques dependiendo de si se conoce o no la covarianza entre los diferentes valores p.

El método de Brown se puede utilizar para combinar valores p dependientes cuyas estadísticas de prueba subyacentes tienen una distribución normal multivariada con una matriz de covarianza conocida. El método de Kost extiende el de Brown para permitir combinar valores p cuando la matriz de covarianza se conoce solo hasta un factor multiplicativo escalar.

El valor p de media armónica ofrece una alternativa al método de Fisher para combinar valores p cuando se desconoce la estructura de dependencia pero no se puede suponer que las pruebas sean independientes.

El método de Fisher se aplica normalmente a una colección de estadísticas de prueba independientes, normalmente de estudios separados que tienen la misma hipótesis nula. La hipótesis nula del metanálisis es que todas las hipótesis nulas independientes son verdaderas. La hipótesis alternativa del metanálisis es que al menos una de las hipótesis alternativas independientes es verdadera.

En algunos contextos, tiene sentido considerar la posibilidad de "heterogeneidad", en la que la hipótesis nula se cumple en algunos estudios pero no en otros, o en la que diferentes hipótesis alternativas pueden cumplirse en diferentes estudios. Una razón común para la última forma de heterogeneidad es que los tamaños del efecto pueden diferir entre poblaciones. Por ejemplo, considere una colección de estudios médicos que analizan el riesgo de una dieta alta en glucosa para desarrollar diabetes tipo II. Debido a factores genéticos o ambientales, el riesgo real asociado con un nivel dado de consumo de glucosa puede ser mayor en algunas poblaciones humanas que en otras.

En otros contextos, la hipótesis alternativa es universalmente falsa o universalmente verdadera: no hay posibilidad de que se cumpla en algunos contextos pero no en otros. Por ejemplo, considere varios experimentos diseñados para probar una ley física particular. Cualquier discrepancia entre los resultados de estudios o experimentos separados debe deberse al azar, posiblemente impulsado por diferencias en la potencia.

En el caso de un metanálisis que utilice pruebas bilaterales, es posible rechazar la hipótesis nula del metanálisis incluso cuando los estudios individuales muestran efectos fuertes en direcciones diferentes. En este caso, rechazamos la hipótesis de que la hipótesis nula es verdadera en todos los estudios, pero esto no implica que exista una hipótesis alternativa uniforme que se cumpla en todos los estudios. Por lo tanto, el metanálisis bilateral es particularmente sensible a la heterogeneidad en las hipótesis alternativas. El metanálisis unilateral puede detectar heterogeneidad en las magnitudes de los efectos, pero se centra en una única dirección del efecto preestablecida.

Un enfoque estrechamente relacionado con el método de Fisher es el método Z de Stouffer, basado en puntuaciones Z en lugar de valores p, lo que permite la incorporación de ponderaciones de estudio. Recibe su nombre en honor al sociólogo Samuel A. Stouffer. Si hacemos que Z_i = Φ ^{− 1}(1−p_i), donde Φ es la función de distribución acumulativa normal estándar, entonces

${\displaystyle Z\sim ¿Qué?$

es una puntuación Z para el metanálisis general. Esta puntuación Z es apropiada para valores p unilaterales de cola derecha; se pueden realizar modificaciones menores si se analizan valores p bilaterales o de cola izquierda. Específicamente, si se analizan valores p bilaterales, se utiliza el valor p bilateral (p_i/2), o 1-p_i si se utilizan valores p de cola izquierda.

Dado que el método de Fisher se basa en el promedio de los valores −log(p_i), y el método de puntuación Z se basa en el promedio de los valores Z_i, la relación entre estos dos enfoques se deduce de la relación entre z y −log(p) = −log(1−Φ(z)). Para la distribución normal, estos dos valores no están perfectamente relacionados linealmente, pero siguen una relación altamente lineal en el rango de valores Z observados con mayor frecuencia, de 1 a 5. Como resultado, la potencia del método de puntuación Z es casi idéntica a la potencia del método de Fisher.

Una ventaja del método de puntuación Z es que es sencillo introducir ponderaciones. Si la puntuación Z i^ésima se pondera con w_i, entonces la puntuación Z del metanálisis es

${\displaystyle Z\sim ¿Qué? ¿Qué?$

que sigue una distribución normal estándar bajo la hipótesis nula. Si bien se pueden derivar versiones ponderadas de la estadística de Fisher, la distribución nula se convierte en una suma ponderada de estadísticas de chi-cuadrado independientes, con las que resulta menos conveniente trabajar.

• Extensiones del método de Fisher
• Una fuente alternativa para la nota de Fisher de 1948: [1]
• El Fisher, el Z-score de Stouffer, y algunos métodos relacionados se implementan en el paquete de metap R.