Eje radical

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Todos los puntos cuyas distancias relativas a dos círculos son iguales

Dos círculos, centrados en $M 1, M 2$

Eje radical, con punto de muestra $P$

Distancias de ambos círculos a $P$
Las líneas tangentes deben ser iguales en longitud para cualquier punto en el eje radical: ${displaystyle |PT_{1}|=|PT_{2}|.}$ Si $P, T 1, T 2$ yace en un tangente común, entonces $P$ es el punto medio de ${displaystyle {overline {T_{1}T_{2}}}.}$

En geometría euclidiana, el eje radical de dos circunferencias no concéntricas es el conjunto de puntos cuyas potencias respecto de las circunferencias son iguales. Por esta razón el eje radical también se llama línea eléctrica o bisectriz de los dos círculos. En detalle:

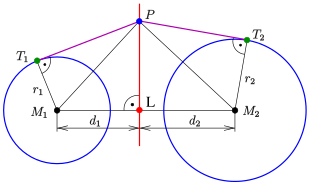
Para dos círculos $c 1, c 2$ con centros $M 1, M 2$ y radios $r 1, r 2$ las potencias de un punto $P$ con respecto a los círculos son

{displaystyle Pi _{1}(P)=|PM_{1}|^{2}-r_{1}^{2},qquad Pi _{2}(P)=|PM_{2}|^{2}-r_{2}^{2}.}

El punto $P$ pertenece al eje radical, si

{displaystyle Pi _{1}(P)=Pi _{2}(P).}

Si los círculos tienen dos puntos en común, el eje radical es la línea común de secant de los círculos.
Si punto $P$ está fuera de los círculos, $P$ tiene igual distancia tangencial a ambos círculos.
Si el radio es igual, el eje radical es el bisector de la línea $M 1, M 2$ .
En cualquier caso, el eje radical es una línea perpendicular a ${displaystyle {overline {M_{1}M_{2}}}.}$

Sobre notaciones

La notación eje radical fue utilizada por el matemático francés M. Chasles como radical de hacha.
J.V. Poncelet utilizó chorde ideale.
J. Plücker introdujo el término Chordale.
J. Steiner llamó al eje radical línea de poderes iguales (en alemán: Linie der gleichen Potenzen) que condujo a la línea de poder (Potenzgerade).

Propiedades

Forma geométrica y su posición

Vamos. ${displaystyle {vec {x}},{vec {m}}_{1},{vec {m}}_{2}}$ ser los vectores de posición de los puntos ${displaystyle P,M_{1},M_{2}}$ . Entonces la ecuación definitoria de la línea radical se puede escribir como:

{displaystyle ({vec {x}}-{vec {m}}_{1})^{2}-r_{1}^{2}=({vec {x}}-{vec {m}}_{2})^{2}-r_{2}^{2}quad leftrightarrow quad 2{vec {x}}cdot ({vec {m}}_{2}-{vec {m}}_{1})+{vec {m}}_{1}^{2}-{vec {m}}_{2}^{2}+r_{2}^{2}-r_{1}^{2}=0}

Definición y cálculo ${displaystyle d_{1},d_{2}}$

De la ecuación correcta se obtiene

El eje radical es de hecho un línea y es perpendicular a la línea a través de los centros del círculo.

() ${displaystyle {vec {m}}_{2}-{vec {m}}_{1}}$ es un vector normal para el eje radical !)

Dividir la ecuación por ${displaystyle 2|{vec {m}}_{2}-{vec {m}}_{1}|}$ Uno tiene la forma normal de Hess. La inserción de los vectores de posición de los centros produce las distancias de los centros al eje radical:

{displaystyle d_{1}={frac {d^{2}+{r_{1}}^{2}-{r_{2}}^{2}}{2d}}\qquad d_{2}={frac {d^{2}+{r_{2}}^{2}-{r_{1}}^{2}}{2d}}}

con

{displaystyle d=|M_{1}M_{2}|}

() ${displaystyle d_{i}}$ puede ser negativo si ${displaystyle L}$ no es entre ${displaystyle M_{1},M_{2}}$ )

Si los círculos se cruzan en dos puntos, la línea radical pasa por los puntos comunes. Si sólo se tocan, la línea radical es la tangente común.

Posiciones especiales

El eje radical de dos círculos de intersección es su línea común de secant.

El eje radical de dos círculos táctiles es su tangente común.

El eje radical de dos no los círculos de intersección es el secant común de dos círculos de equipower convenientes (ver abajo).

Círculos ortogonales

Los puntos de contacto de los tangentes a través de ${displaystyle P}$ miente en el círculo ortogonal (verde)

Para un punto ${displaystyle P}$ fuera de un círculo ${displaystyle c_{i}}$ y los dos puntos tangentes ${displaystyle S_{i},T_{i}}$ la ecuación ${displaystyle |PS_{i}|^{2}=|PT_{i}|^{2}=Pi _{i}(P)}$ tenencias y ${displaystyle S_{i},T_{i}}$ miente en el círculo ${displaystyle c_{o}}$ con centro ${displaystyle P}$ y radio ${displaystyle {sqrt {Pi _{i}(P)}}}$ . Circle ${displaystyle c_{o}}$ intersects ${displaystyle c_{i}}$ ortogonal. Por lo tanto:

{displaystyle P}

es un punto del eje radical, luego los cuatro puntos

{displaystyle S_{1},T_{1},S_{2},T_{2}}

miente en círculo

{displaystyle c_{o}}

, que interseca los círculos dados

{displaystyle c_{1},c_{2}}

ortogonal.

El eje radical consiste en todo centros de círculos, que intersectan los círculos dados ortogonalmente.

Sistema de círculos ortogonales

El método descrito en la sección anterior para la construcción de un lápiz de círculos, que intersecan ortogonalmente dos círculos dados, se puede extender a la construcción de dos sistemas de círculos que se cruzan ortogonalmente:

Vamos. ${displaystyle c_{1},c_{2}}$ ser dos círculos de mentira separados (como en la sección anterior), ${displaystyle M_{1},M_{2},r_{1},r_{2}}$ sus centros y radios y ${displaystyle g_{12}}$ su eje radical. Ahora, todos los círculos se determinarán con centros en línea ${displaystyle {overline {M_{1}M_{2}}}}$ , que tienen junto con ${displaystyle c_{1}}$ línea ${displaystyle g_{12}}$ como eje radical, también. Si ${displaystyle gamma _{2}}$ es un círculo tal, cuyo centro tiene distancia ${displaystyle delta }$ al centro ${displaystyle M_{1}}$ y radio ${displaystyle rho _{2}}$ . Del resultado en la sección anterior se obtiene la ecuación

{displaystyle d_{1}={frac {delta ^{2}+r_{1}^{2}-rho _{2}^{2}}{2delta }}quad }

, donde

r_{1}}" xmlns="http://www.w3.org/1998/Math/MathML">d1■r1{displaystyle ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪r_{1}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d69ecfc290cf5f1b2c7e583407b21eb425f46d63" style="vertical-align: -0.671ex; width:7.464ex; height:2.509ex;"/>

están arreglados.

Con ${displaystyle delta _{2}=delta -d_{1}}$ la ecuación puede ser reescrita como:

{displaystyle delta _{2}^{2}=d_{1}^{2}-r_{1}^{2}+rho _{2}^{2}}

Sistema de círculos ortogonales: construcción

Si el radio ${displaystyle rho _{2}}$ se da, de esta ecuación se encuentra la distancia ${displaystyle delta _{2}}$ al eje radical (fijo) del nuevo centro. En el diagrama el color de los nuevos círculos es púrpura. Cualquier círculo verde (ver diagrama) tiene su centro en el eje radical e interseca los círculos ${displaystyle c_{1},c_{2}}$ ortogonalmente y por lo tanto todos los nuevos círculos (purple), también. Elegir el eje radical (rojo) como eje y línea ${displaystyle {overline {M_{1}M_{2}}}}$ como eje x, los dos lápices de círculos tienen las ecuaciones:

morado:

{displaystyle (x-delta _{2})^{2}+y^{2}=delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}}

verde:

{displaystyle x^{2}+(y-y_{g})^{2}=y_{g}^{2}+d_{1}^{2}-r_{1}^{2}.}

() ${displaystyle ;(0,y_{g})}$ es el centro de un círculo verde.)

Propiedades:
a) Cualquier dos círculos verdes se intersectan en el eje x en los puntos ${displaystyle P_{1/2}={big (}pm {sqrt {d_{1}^{2}-r_{1}^{2}}},0{big)}}$ , el postes del sistema ortogonal de los círculos. Eso significa que el eje x es la línea radical de los círculos verdes.
b) Los círculos púrpura no tienen puntos en común. Pero, si uno considera el plano real como parte del plano complejo, entonces cualquier dos círculos púrpura se intersectan en el eje y (su eje radical común) en los puntos ${displaystyle Q_{1/2}={big (}0,pm i{sqrt {d_{1}^{2}-r_{1}^{2}}}{big)}}$ .

Casos especiales:
a) En caso de ${displaystyle d_{1}=r_{1}}$ los círculos verdes se tocan entre sí en el origen con el eje x como tangente común y los círculos púrpuras tienen el eje y como tangente común. Tal sistema de círculos se llama círculos parabólicos coaxales (véase infra).
b) Arrugando ${displaystyle c_{1}}$ a su centro ${displaystyle M_{1}}$ , i. e. ${displaystyle r_{1}=0}$ , las ecuaciones se convierten en una forma más simple y uno consigue ${displaystyle M_{1}=P_{1}}$ .

Conclusión:
a) Para cualquier real ${displaystyle w}$ el lápiz de los círculos

{displaystyle ;c(xi):;(x-xi)^{2}+y^{2}-xi ^{2}-w=0:}

tiene la propiedad: El eje y es el eje radical de

{displaystyle c(xi _{1}),c(xi _{2})}

En caso de

0}" xmlns="http://www.w3.org/1998/Math/MathML">w■0{displaystyle w título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/64211aba3d32f9d4210040b6d00ddc249ed84bbb" style="vertical-align: -0.338ex; width:5.925ex; height:2.176ex;"/>

los círculos

{displaystyle c(xi _{1}),c(xi _{2})}

intersección en puntos

{displaystyle P_{1/2}=(0,pm {sqrt {w}})}

En caso de

<math alttext="{displaystyle wwc)0{displaystyle w made0} <img alt="{displaystyle w

no tienen puntos en común.

En caso de

{displaystyle w=0}

se tocan

{displaystyle (0,0)}

y el eje y es su tangente común.

b) Para cualquier real ${displaystyle w}$ los dos lápices de círculos

{displaystyle c_{1}(xi):;(x-xi)^{2}+y^{2}-xi ^{2}-w=0}

{displaystyle c_{2}(eta):;x^{2}+(y-eta)^{2}-eta ^{2}+w=0 }

forma sistema de círculos ortogonales. Eso significa: dos círculos

{displaystyle c_{1}(xi),c_{2}(eta)}

intersect ortogonalmente.

c) De las ecuaciones en b), se obtiene una representación libre de coordenadas:

Sistema ortogonal de círculos a postes dados ${displaystyle P_{1},P_{2}}$

Para los puntos dados

{displaystyle P_{1},P_{2}}

, su punto medio

{displaystyle O}

y su bisector lineal

{displaystyle g_{12}}

las dos ecuaciones

{displaystyle |XM|^{2}=|OM|^{2}-|OP_{1}|^{2}}

{displaystyle |XN|^{2}=|ON|^{2}+|OP_{1}|^{2}=|NP_{1}|^{2}}

con

{displaystyle M}

{displaystyle {overline {P_{1}P_{2}}}}

pero no entre

{displaystyle P_{1},P_{2}}

, y

{displaystyle N}

{displaystyle g_{12}}

describir el sistema ortogonal de los círculos determinado por

{displaystyle P_{1},P_{2}}

que son los polos del sistema.

Para

{displaystyle P_{1}=P_{2}=O}

uno tiene que prescribir los ejes

{displaystyle a_{1},a_{2}}

del sistema, también. El sistema es parabólica:

{displaystyle |XM|^{2}=|OM|^{2}\quad |XN|^{2}=|ON|^{2}}

con

{displaystyle M}

{displaystyle a_{1}}

{displaystyle N}

{displaystyle a_{2}}

Construcción con regla y compás:

Sistema ortogonal de círculos: hendidura y brújula construcción

Un sistema de círculos ortogonales se determina únicamente por sus polos ${displaystyle P_{1},P_{2}}$ :

Los ejes ( ejes radicales) son las líneas ${displaystyle {overline {P_{1}P_{2}}}}$ y el bisector del segmento de línea ${displaystyle g_{12}}$ de los polos.
Los círculos (verde en el diagrama) por ${displaystyle P_{1},P_{2}}$ tener sus centros en ${displaystyle g_{12}}$ . Se pueden dibujar fácilmente. Para un punto ${displaystyle N}$ el radio es ${displaystyle ;r_{N}=|NP_{1}|;}$ .
Para dibujar un círculo del segundo lápiz (en el diagrama azul) con el centro ${displaystyle M}$ on ${displaystyle {overline {P_{1}P_{2}}}}$ , uno determina el radio ${displaystyle r_{M}}$ aplicando el teorema de Pitágoras: ${displaystyle ;r_{M}^{2}=|OM|^{2}-|OP_{1}|^{2};}$ (ver diagrama).

En caso de ${displaystyle P_{1}=P_{2}}$ los ejes tienen que ser elegidos adicionalmente. El sistema es parabólico y se puede dibujar fácilmente.

Círculos coaxiales

Definición y propiedades:

Vamos. ${displaystyle c_{1},c_{2}}$ ser dos círculos y ${displaystyle Pi _{1},Pi _{2}}$ sus funciones de poder. Entonces para cualquier ${displaystyle lambda neq 1}$

${displaystyle Pi _{1}(x,y)-lambda Pi _{2}(x,y)=0}$

es la ecuación de un círculo ${displaystyle c(lambda)}$ (véase infra). Tal sistema de círculos se llama círculos coaxiales generados por los círculos ${displaystyle c_{1},c_{2}}$ . (En caso de ${displaystyle lambda =1}$ la ecuación describe el eje radical ${displaystyle c_{1},c_{2}}$ )

La función de potencia ${displaystyle c(lambda)}$ es

{displaystyle Pi (lambdax,y)={frac {Pi _{1}(x,y)-lambda Pi _{2}(x,y)}{1-lambda }}}

El normed ecuación (los coeficientes de ${displaystyle x^{2},y^{2}}$ son ${displaystyle 1}$ ) de ${displaystyle c(lambda)}$ es ${displaystyle Pi (lambdax,y)=0}$ .

Un cálculo simple muestra:

${displaystyle c(lambda),c(mu), lambda neq mu }$ tienen el mismo eje radical que ${displaystyle c_{1},c_{2}}$ .

Permiso ${displaystyle lambda }$ para pasar al infinito, uno reconoce, que ${displaystyle c_{1},c_{2}}$ son miembros del sistema de círculos coaxales: ${displaystyle c_{1}=c(0),;c_{2}=c(infty)}$ .

(E): Si ${displaystyle c_{1},c_{2}}$ intersect en dos puntos ${displaystyle P_{1},P_{2}}$ , cualquier círculo ${displaystyle c(lambda)}$ contiene ${displaystyle P_{1},P_{2}}$ , también, y la línea ${displaystyle {overline {P_{1}P_{2}}}}$ es su eje radical común. Tal sistema se llama elíptico.
(P): Si ${displaystyle c_{1},c_{2}}$ son tangente a ${displaystyle P}$ , cualquier círculo es tangente ${displaystyle c_{1},c_{2}}$ punto ${displaystyle P}$ , también. El tangente común es su eje radical común. Tal sistema se llama parabólica.
(H): Si ${displaystyle c_{1},c_{2}}$ han tenido no punto en común, entonces cualquier par del sistema, también. El eje radical de cualquier par de círculos es el eje radical de ${displaystyle c_{1},c_{2}}$ . El sistema se llama hiperbólico.

En detalle:

Introduciendo coordenadas tales que

{displaystyle c_{1}:(x-d_{1})^{2}+y^{2}=r_{1}^{2}}

{displaystyle c_{2}:(x-d_{2})^{2}+y^{2}=d_{2}^{2}+r_{1}^{2}-d_{1}^{2}}

entonces el eje y es su eje radical (ver arriba).

Calculando la función de potencia ${displaystyle Pi (lambdax,y)}$ da la ecuación del círculo normalizado:

{displaystyle c(lambda): x^{2}+y^{2}-2{tfrac {d_{1}-lambda d_{2}}{1-lambda }};x+d_{1}^{2}-r_{1}^{2}=0.}

Completar la plaza y la sustitución ${displaystyle delta _{2}={tfrac {d_{1}-lambda d_{2}}{1-lambda }}}$ (x-coordinado del centro) produce la forma centrada de la ecuación

{displaystyle c(lambda): (x-delta _{2})^{2}+y^{2}=delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}}

En caso de $d_{1}}" xmlns="http://www.w3.org/1998/Math/MathML">r1■d1{displaystyle [R_{1}]d_{1}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9fa87efe281b92df990c7eefdbeaaa115a317a" style="vertical-align: -0.671ex; width:7.464ex; height:2.509ex;"/>$ los círculos ${displaystyle c_{1},c_{2},c(lambda)}$ tienen los dos puntos

{displaystyle P_{1}={big (}0,{sqrt {r_{1}^{2}-d_{1}^{2}}}{big)},quad P_{2}={big (}0,-{sqrt {r_{1}^{2}-d_{1}^{2}}}{big)}}

en común y el sistema de círculos coaxiales es elíptico.

En caso de ${displaystyle r_{1}=d_{1}}$ los círculos ${displaystyle c_{1},c_{2},c(lambda)}$ punto ${displaystyle P_{0}=(0,0)}$ en común y el sistema es parabólica.

En caso de $<math alttext="{displaystyle r_{1}r1c)d1{displaystyle [R]}<img alt="{displaystyle r_{1}$ los círculos ${displaystyle c_{1},c_{2},c(lambda)}$ no tiene sentido en común y el sistema es hiperbólico.

Ecuaciones alternativas:
1) En la ecuación definitoria de un sistema coaxial de círculos también se pueden utilizar múltiplos de las funciones de potencia.
2) La ecuación de uno de los círculos se puede sustituir por la ecuación del eje radical deseado. El eje radical puede verse como un círculo con un radio infinitamente grande. Por ejemplo:

{displaystyle (x-x_{1})^{2}+y^{2}-r_{1}^{2} - lambda ;2(x-x_{2}) =0 Leftrightarrow }

{displaystyle (x-(x_{1}+lambda))^{2}+y^{2}=(x_{1}+lambda)^{2}+r_{1}^{2}-x_{1}^{2}-2lambda x_{2}}

describe todos los círculos, que tienen con el primer círculo la línea ${displaystyle x=x_{2}}$ como eje radical.
3) Para expresar la igualdad de condiciones de los dos círculos, a menudo se utiliza la siguiente forma:

{displaystyle mu Pi _{1}(x,y)+nu Pi _{2}(x,y)=0;.}

Pero en este caso la representación de un círculo por los parámetros ${displaystyle munu }$ es no único.

Aplicaciones:
a) Las inversiones circulares y las transformaciones de Möbius conservan ángulos y círculos generalizados. Por lo tanto, los sistemas ortogonales de los círculos desempeñan un papel esencial en las investigaciones sobre estos mapas.
b) En los círculos coaxales de electromagnetismo aparecen como líneas de campo.

Centro radical de tres círculos, construcción del eje radical

Centro radical de tres círculos
El círculo verde intersecte los tres círculos ortogonalmente.

Para tres círculos ${displaystyle c_{1},c_{2},c_{3}}$ , no hay dos de los cuales son concéntricos, hay tres ejes radicales ${displaystyle g_{12},g_{23},g_{31}}$ . Si los centros del círculo no se encuentran en una línea, los ejes radicales se intersectan en un punto común ${displaystyle R}$ , el centro radical de los tres círculos. El círculo ortogonal se centró alrededor ${displaystyle R}$ de dos círculos es ortogonal al tercer círculo, también (círculo radical).

Prueba: el eje radical

{displaystyle g_{ik}}

contiene todos los puntos que tienen igual distancia tangencial a los círculos

{displaystyle c_{i},c_{k}}

. El punto de intersección

{displaystyle R}

{displaystyle g_{12}}

{displaystyle g_{23}}

tiene la misma distancia tangencial a los tres círculos. Por lo tanto

{displaystyle R}

es un punto del eje radical

{displaystyle g_{31}}

, también.

Esta propiedad permite uno a construcción el eje radical de dos círculos no intersectos

{displaystyle c_{1},c_{2}}

con centros

{displaystyle M_{1},M_{2}}

: Dibuja un tercer círculo

{displaystyle c_{3}}

con centro no collinear a los centros dados que intersectan

{displaystyle c_{1},c_{2}}

. Los ejes radicales

{displaystyle g_{13},g_{23}}

se puede dibujar. Su punto de intersección es el centro radical

{displaystyle R}

de los tres círculos y

{displaystyle g_{12}}

. La línea a través

{displaystyle R}

que es perpendicular a

{displaystyle {overline {M_{1}M_{2}}}}

es el eje radical

{displaystyle g_{12}}

Método de construcción adicional:

Construcción del eje radical con círculos ${displaystyle c'_{1},c'_{2}}$ de igual poder. Es ${displaystyle Pi _{1}(P_{1})=Pi _{2}(P_{2})}$ .

Todos los puntos que tienen el mismo poder de un círculo dado ${displaystyle c}$ miente en un círculo concéntrico ${displaystyle c}$ . Vamos a llamarlo un equipower circle. Esta propiedad se puede utilizar para un método de construcción adicional del eje radical de dos círculos:

Para dos círculos que no intersectan ${displaystyle c_{1},c_{2}}$ , se pueden dibujar dos círculos de equipower ${displaystyle c'_{1},c'_{2}}$ , que tienen el mismo poder con respecto a ${displaystyle c_{1},c_{2}}$ (ver diagrama). En detalle: ${displaystyle Pi _{1}(P_{1})=Pi _{2}(P_{2})}$ . Si el poder es lo suficientemente grande, los círculos ${displaystyle c'_{1},c'_{2}}$ tienen dos puntos en común, que se encuentran en el eje radical ${displaystyle g_{12}}$ .

Relación con las coordenadas bipolar

En general, los dos círculos disyuntivos no concéntricos pueden alinearse con los círculos de un sistema de coordenadas bipolar. En ese caso, el eje radical es simplemente el ${displaystyle y}$ -eje de este sistema de coordenadas. Cada círculo en el eje que pasa a través de los dos focos del sistema de coordenadas interseca los dos círculos ortogonalmente. Una colección máxima de círculos, todos los que tienen centros en una línea dada y todos los pares que tienen el mismo eje radical, se conoce como un lápiz de círculos coaxales.

Centro radical en coordenadas trilineales

Si los círculos se representan en coordenadas trilineales de la forma habitual, entonces su centro radical se da convenientemente como un determinado determinante. Específicamente, sea X = x: y: z un punto variable en el plano de un triángulo ABC con longitudes laterales a = |BC|, b = |CA|, c = |AB|, y representa los círculos de la siguiente manera:

()dx + ey + fz)ax + por + cz) + g()ayz + bzx + cxy) = 0

()hx + iy + jz)ax + por + cz) + k()ayz + bzx + cxy) = 0

()lx + mi + nz)ax + por + cz) + p()ayz + bzx + cxy) = 0

Entonces el centro radical es el punto

{displaystyle det {begin{bmatrix}g&k&p\e&i&m\f&j&nend{bmatrix}}:det {begin{bmatrix}g&k&p\f&j&n\d&h&lend{bmatrix}}:det {begin{bmatrix}g&k&p\d&h&l\e&i&mend{bmatrix}}.}

Plano radical e hiperplano

El plano radical de dos esferas no concéntricas en tres dimensiones se define de manera similar: es el lugar geométrico de los puntos a partir de los cuales las tangentes a las dos esferas tienen la misma longitud. El hecho de que este lugar sea un plano se deriva, por rotación en la tercera dimensión, del hecho de que el eje radical es una línea recta.

La misma definición se puede aplicar a hiperesferas en el espacio euclidiano de cualquier dimensión, dando el hiperplano radical de dos hiperesferas no concéntricas.

Más resultados...