Efecto zeeman

ImprimirCitar

Línea espectral dividida en campo magnético

Las líneas espectrales de la lámpara de vapor de mercurio a longitud de onda 546.1 nm, mostrando efecto anómalo Zeeman. (A) Sin campo magnético. (B) Con campo magnético, las líneas espectrales se dividen como efecto transversal de Zeeman. (C) Con campo magnético, dividido como efecto longitudinal de Zeeman. Las líneas espectrales se obtuvieron utilizando un interferómetro Fabry-Pérot.

Zeeman división del nivel 5 de 87Rb, incluyendo estructura fina y división de estructura hiperfina. Aquí. F=J+I, donde I es el giro nuclear (para ⁸⁷Rb, I=3.2).

Esta animación muestra lo que sucede como un solar (o estrellaspot) formas y el campo magnético aumenta en la fuerza. La luz emergente del lugar comienza a demostrar el efecto Zeeman. Las líneas de espectro oscuro en el espectro de la luz emitida se dividen en tres componentes y la fuerza de la polarización circular en partes del espectro aumenta significativamente. Este efecto de polarización es una poderosa herramienta para que los astrónomos detecten y miden campos magnéticos estelares.

El efecto Zeeman (pronunciación holandesa: [ˈzeːmɑn]) es el efecto de dividir una línea espectral en varios componentes en presencia de un campo magnético estático. Lleva el nombre del físico holandés Pieter Zeeman, quien lo descubrió en 1896 y recibió un premio Nobel por este descubrimiento. Es análogo al efecto Stark, la división de una línea espectral en varios componentes en presencia de un campo eléctrico. También similar al efecto Stark, las transiciones entre diferentes componentes tienen, en general, diferentes intensidades, y algunas están totalmente prohibidas (en la aproximación dipolar), según lo rigen las reglas de selección.

Dado que la distancia entre los subniveles de Zeeman es una función de la intensidad del campo magnético, este efecto se puede utilizar para medir la intensidad del campo magnético, p. la del Sol y otras estrellas o en plasmas de laboratorio. El efecto Zeeman es muy importante en aplicaciones como la espectroscopia de resonancia magnética nuclear, la espectroscopia de resonancia de espín de electrones, la formación de imágenes por resonancia magnética (IRM) y la espectroscopia de Mössbauer. También se puede utilizar para mejorar la precisión en la espectroscopia de absorción atómica. Una teoría sobre el sentido magnético de las aves supone que una proteína en la retina cambia debido al efecto Zeeman.

Cuando las líneas espectrales son líneas de absorción, el efecto se denomina efecto Zeeman inverso.

Nomenclatura

Históricamente, se distingue entre el normal y un efecto Zeeman anómalo (descubierto por Thomas Preston en Dublín, Irlanda). El efecto anómalo aparece en las transiciones donde el giro neto de los electrones es distinto de cero. Fue llamado "anómalo" porque el espín del electrón aún no se había descubierto, por lo que no había una buena explicación para él en el momento en que Zeeman observó el efecto. Wolfgang Pauli recuerda que cuando un colega le preguntó por qué parecía infeliz, respondió: "¿Cómo puede uno parecer feliz cuando piensa en el anómalo efecto Zeeman?".

A mayor intensidad de campo magnético, el efecto deja de ser lineal. A intensidades de campo aún mayores, comparables a la intensidad del campo interno del átomo, el acoplamiento de electrones se altera y las líneas espectrales se reorganizan. Esto se llama el efecto Paschen-Back.

En la literatura científica moderna, estos términos rara vez se usan, con una tendencia a usar solo el "efecto Zeeman".

Presentación teórica

El hamiltoniano total de un átomo en un campo magnético es

{displaystyle H=H_{0}+V_{rm {M}}, }

Donde $H_{0}$ es el Hamiltoniano no perturbado del átomo, y ${displaystyle V_{rm {M}}}$ es la perturbación debido al campo magnético:

{displaystyle V_{rm {M}}=-{vec {mu }}cdot {vec {B}},}

Donde $vec{mu}$ es el momento magnético del átomo. El momento magnético consiste en las partes electrónicas y nucleares; sin embargo, este último es muchas órdenes de magnitud más pequeñas y será descuidado aquí. Por lo tanto,

{displaystyle {vec {mu }}approx -{frac {mu _{rm {B}}g{vec {J}}}{hbar }},}

Donde ${displaystyle mu _{rm {B}}}$ es el imán Bohr, ${vec {J}}$ es el impulso angular electrónico total, y $g$ es el factor Landé. Un enfoque más preciso es tener en cuenta que el operador del momento magnético de un electrón es una suma de las contribuciones del impulso angular orbital $vec L$ y el impulso angular del giro $vec S$ , con cada multiplicado por la proporción giromagnetica adecuada:

{displaystyle {vec {mu }}=-{frac {mu _{rm {B}}(g_{l}{vec {L}}+g_{s}{vec {S}})}{hbar }},}

Donde $g_l = 1$ y $g_s approx 2.0023192$ (este último se llama la relación gimagnética anómala; la desviación del valor de 2 se debe a los efectos de la electrodinámica cuántica). En el caso del acoplamiento de LS, se puede resumir todos los electrones en el átomo:

g vec{J} = leftlanglesum_i (g_l vec{l_i} + g_s vec{s_i})rightrangle = leftlangle (g_lvec{L} + g_s vec{S})rightrangle,

Donde ${vec {L}}$ y ${vec {S}}$ son el impulso orbital total y el giro del átomo, y el promedio se hace sobre un estado con un valor dado del impulso angular total.

Si el término de interacción $V_M$ es pequeña (menos que la estructura fina), se puede tratar como una perturbación; este es el efecto Zeeman adecuado. En el efecto Paschen–Back, descrito a continuación, $V_M$ supera el acoplamiento LS significativamente (pero sigue siendo pequeño en comparación con $H_{0}$ ). En campos magnéticos ultrafuertes, la interacción del campo magnético puede exceder $H_{0}$ , en cuyo caso el átomo ya no puede existir en su significado normal, y uno habla sobre los niveles de Landau en su lugar. Hay casos intermedios que son más complejos que estos casos límite.

Campo débil (efecto Zeeman)

Si la interacción espina-órbita domina sobre el efecto del campo magnético externo, ${displaystyle {vec {L}}}$ y ${displaystyle {vec {S}}}$ no se conservan por separado, sólo el impulso angular total ${displaystyle {vec {J}}={vec {L}}+{vec {S}}}$ Lo es. Los vectores de impulso angular giratorio y orbital se pueden considerar como precesante sobre el vector de impulso angular total (fijado) ${displaystyle {vec {J}}}$ . El (time-)"averaged" spin vector es entonces la proyección de la vuelta en la dirección de ${displaystyle {vec {J}}}$ :

{displaystyle {vec {S}}_{rm {avg}}={frac {({vec {S}}cdot {vec {J}})}{J^{2}}}{vec {J}}}

y para el (tiempo-)"promedio" vectores orbitales:

{displaystyle {vec {L}}_{rm {avg}}={frac {({vec {L}}cdot {vec {J}})}{J^{2}}}{vec {J}}.}

Por lo tanto,

{displaystyle langle V_{rm {M}}rangle ={frac {mu _{rm {B}}}{hbar }}{vec {J}}left(g_{L}{frac {{vec {L}}cdot {vec {J}}}{J^{2}}}+g_{S}{frac {{vec {S}}cdot {vec {J}}}{J^{2}}}right)cdot {vec {B}}.}

Uso ${displaystyle {vec {L}}={vec {J}}-{vec {S}}}$ y balanceando ambos lados, obtenemos

vec S cdot vec J = frac{1}{2}(J^2 + S^2 - L^2) = frac{hbar^2}{2}[j(j+1) - l(l+1) + s(s+1)],

y: utilizando ${displaystyle {vec {S}}={vec {J}}-{vec {L}}}$ y balanceando ambos lados, obtenemos

vec L cdot vec J = frac{1}{2}(J^2 - S^2 + L^2) = frac{hbar^2}{2}[j(j+1) + l(l+1) - s(s+1)].

Combinar todo y tomar ${displaystyle J_{z}=hbar m_{j}}$ , obtenemos la energía potencial magnética del átomo en el campo magnético externo aplicado,

{displaystyle {begin{aligned}V_{rm {M}}&=mu _{rm {B}}Bm_{j}left[g_{L}{frac {j(j+1)+l(l+1)-s(s+1)}{2j(j+1)}}+g_{S}{frac {j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}}right]\&=mu _{rm {B}}Bm_{j}left[1+(g_{S}-1){frac {j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}}right],\&=mu _{rm {B}}Bm_{j}g_{j}end{aligned}}}

donde la cantidad entre corchetes es el Landé g-factor g_J del átomo ( $g_L = 1$ y $g_S approx 2$ ) y $m_{j}$ es el componente z del impulso angular total. Para un solo electrón sobre las cáscaras llenas $s = 1/2$ y $j = l pm s$ , el factor Landé puede ser simplificado en:

g_j = 1 pm frac{g_S-1}{2l+1}

Tomando $V_{m}$ para ser la perturbación, la corrección Zeeman a la energía es

{displaystyle {begin{aligned}E_{rm {Z}}^{(1)}=langle nljm_{j}|H_{rm {Z}}^{'}|nljm_{j}rangle =langle V_{M}rangle _{Psi }=mu _{rm {B}}g_{J}B_{rm {ext}}m_{j}end{aligned}}}

Ejemplo: transición Lyman-alfa en hidrógeno

La transición Lyman-alfa en el hidrógeno en presencia de la interacción espín-órbita implica las transiciones

2P_{1/2} to 1S_{1/2}

2P_{3/2} to 1S_{1/2}.

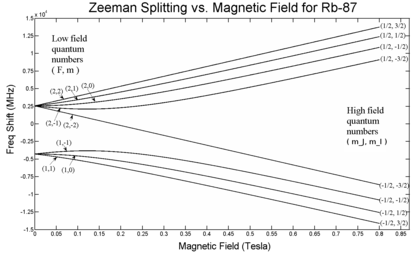
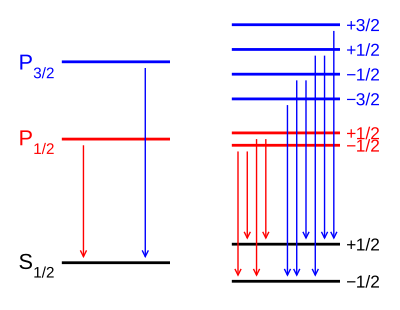
En presencia de un campo magnético externo, el efecto Zeeman de campo débil divide el 1S_1/2 y 2P_1/2 niveles en 2 estados cada uno ( $m_j = 1/2, -1/2$ ) y el 2P_3/2 nivel en 4 estados ( $m_j = 3/2, 1/2, -1/2, -3/2$ ). The Landé g-factors for the three levels are:

g_J = 2

para

1S_{1/2}

(j=1/2, l=0)

g_J = 2/3

para

2P_{1/2}

(j=1/2, l=1)

g_J = 4/3

para

2P_{3/2}

(j=3/2, l=1).

Tenga en cuenta en particular que el tamaño de la división de energía es diferente para los diferentes orbitales, porque los valores de g_J son diferentes. A la izquierda, se representa la división de estructuras finas. Esta división se produce incluso en ausencia de un campo magnético, ya que se debe al acoplamiento espín-órbita. A la derecha se muestra la división adicional de Zeeman, que se produce en presencia de campos magnéticos.

Posibles transiciones para el débil efecto Zeeman
Estado inicial () ${displaystyle n=2,l=1}$ ) ${displaystyle mid j,m_{j}rangle }$	Estado final () ${displaystyle n=1,l=0}$ ) ${displaystyle mid j,m_{j}rangle }$	Energy perturbation
${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle mp {frac {2}{3}}mu _{rm {B}}B}$
${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},mp {frac {1}{2}}rightrangle }$	${displaystyle pm {frac {4}{3}}mu _{rm {B}}B}$
${displaystyle left\|{frac {3}{2}},pm {frac {3}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle pm mu _{rm {B}}B}$
${displaystyle left\|{frac {3}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle mp {frac {1}{3}}mu _{rm {B}}B}$
${displaystyle left\|{frac {3}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},mp {frac {1}{2}}rightrangle }$	${displaystyle pm {frac {5}{3}}mu _{rm {B}}B}$

Campo fuerte (efecto Paschen-Back)

El efecto Paschen–Back es la división de los niveles de energía atómica en presencia de un campo magnético fuerte. Esto ocurre cuando un campo magnético externo es suficientemente fuerte para interrumpir el acoplamiento entre orbital ( ${vec {L}}$ ) y girar ( ${vec {S}}$ Momento angular. Este efecto es el límite de campo fuerte del efecto Zeeman. Cuando $s=0$ , los dos efectos son equivalentes. El efecto fue nombrado por los físicos alemanes Friedrich Paschen y Ernst E. A. Back.

Cuando la perturbación del campo magnético supera significativamente la interacción de la médula espinal, se puede asumir con seguridad $[H_{0}, S] = 0$ . Esto permite los valores de expectativa $L_{z}$ y $S_{z}$ para ser fácilmente evaluado para un estado $|psirangle$ . Las energías son simplemente

{displaystyle E_{z}=leftlangle psi left|H_{0}+{frac {B_{z}mu _{rm {B}}}{hbar }}(L_{z}+g_{s}S_{z})right|psi rightrangle =E_{0}+B_{z}mu _{rm {B}}(m_{l}+g_{s}m_{s}).}

Lo anterior puede leerse como lo que implica que el revestimiento LS está completamente roto por el campo externo. Sin embargo $m_{l}$ y $m_{s}$ son números cuánticos "buenos". Junto con las reglas de selección para una transición del dipolo eléctrico, es decir, $Delta s = 0, Delta m_s = 0, Delta l = pm 1, Delta m_l = 0, pm 1$ esto permite ignorar el grado de tirada de la libertad por completo. Como resultado, sólo tres líneas espectrales serán visibles, correspondientes al $Delta m_l = 0, pm 1$ Regla de selección. La división ${displaystyle Delta E=Bmu _{rm {B}}Delta m_{l}}$ es independiente de las energías no perturbadas y configuraciones electrónicas de los niveles que se están considerando. En general (si $sneq 0$ ), estos tres componentes son en realidad grupos de varias transiciones cada uno, debido al acoplamiento de spin-orbit residual.

En general, ahora se debe agregar el acoplamiento espín-órbita y las correcciones relativistas (que son del mismo orden, conocidas como 'estructura fina') como una perturbación a estas 'imperturbadas' niveles La teoría de la perturbación de primer orden con estas correcciones de estructura fina produce la siguiente fórmula para el átomo de hidrógeno en el límite de Paschen-Back:

{displaystyle E_{z+fs}=E_{z}+{frac {m_{e}c^{2}alpha ^{4}}{2n^{3}}}left{{frac {3}{4n}}-left[{frac {l(l+1)-m_{l}m_{s}}{l(l+1/2)(l+1)}}right]right}.}

Posibles transiciones de Lyman-alpha para el régimen fuerte
Estado inicial () ${displaystyle n=2,l=1}$ ) ${displaystyle mid m_{l},m_{s}rangle }$	Energía inicial Perturbación	Estado final () ${displaystyle n=1,l=0}$ ) ${displaystyle mid m_{l},m_{s}rangle }$
${displaystyle left\|1,{frac {1}{2}}rightrangle }$	${displaystyle pm 2mu _{rm {B}}B_{z}}$	${displaystyle left\|0,{frac {1}{2}}rightrangle }$
${displaystyle left\|0,{frac {1}{2}}rightrangle }$	${displaystyle +mu _{rm {B}}B_{z}}$	${displaystyle left\|0,{frac {1}{2}}rightrangle }$
${displaystyle left\|1,-{frac {1}{2}}rightrangle }$	$0$	${displaystyle left\|0,-{frac {1}{2}}rightrangle }$
${displaystyle left\|-1,{frac {1}{2}}rightrangle }$	$0$	${displaystyle left\|0,{frac {1}{2}}rightrangle }$
${displaystyle left\|0,-{frac {1}{2}}rightrangle }$	${displaystyle -mu _{rm {B}}B_{z}}$	${displaystyle left\|0,-{frac {1}{2}}rightrangle }$
${displaystyle left\|-1,-{frac {1}{2}}rightrangle }$	${displaystyle -2mu _{rm {B}}B_{z}}$	${displaystyle left\|0,-{frac {1}{2}}rightrangle }$

Campo intermedio para j = 1/2

En la aproximación del dipolo magnético, el hamiltoniano que incluye tanto las interacciones hiperfinas como las de Zeeman es

H = h A vec I cdot vec J - vec mu cdot vec B

{displaystyle H=hA{vec {I}}cdot {vec {J}}+(mu _{rm {B}}g_{J}{vec {J}}+mu _{rm {N}}g_{I}{vec {I}})cdot {vec {rm {B}}}}

Donde $A$ es la división hiperfina (en Hz) en el campo magnético cero aplicado, ${displaystyle mu _{rm {B}}}$ y ${displaystyle mu _{rm {N}}}$ son el imán Bohr y el magnetón nuclear respectivamente, ${vec {J}}$ y $vec I$ son el electron y los operadores de impulso angular nuclear y $g_J$ es el factor Landé:

{displaystyle g_{J}=g_{L}{frac {J(J+1)+L(L+1)-S(S+1)}{2J(J+1)}}+g_{S}{frac {J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}}.}

En el caso de los campos magnéticos débiles, la interacción Zeeman puede ser tratada como una perturbación a la $|F,m_f rangle$ base. En el régimen de alto campo, el campo magnético se vuelve tan fuerte que el efecto Zeeman dominará, y uno debe utilizar una base más completa de $|I,J,m_I,m_Jrangle$ o simplemente $|m_I,m_J rangle$ desde entonces $I$ y $J$ será constante dentro de un nivel dado.

Para obtener la imagen completa, incluyendo las fortalezas de campo intermedio, debemos considerar eigenstates que son superposiciones de las $|F,m_F rangle$ y $|m_I,m_J rangle$ Estados de base. Para $J = 1/2$ , el Hamiltonian se puede resolver analíticamente, dando lugar a Breit-Rabi formula. Notablemente, la interacción de cuádrupo eléctrico es cero para $L = 0$ () $J = 1/2$ ), así que esta fórmula es bastante exacta.

Ahora utilizamos operadores de escalera mecánica cuántica, que se definen para un operador de impulso angular general $L$ como

L_{pm} equiv L_x pm iL_y

Estos operadores de escalera tienen la propiedad

L_{pm}|L_,m_L rangle = sqrt{(L mp m_L)(L pm m_L +1)} |L,m_L pm 1 rangle

mientras $m_L$ yace en el rango ${-L, dots...L}$ (otros, vuelven cero). Utilizando operadores de escaleras $J_{pm}$ y $I_{pm}$ Podemos reescribir al Hamiltonian como

{displaystyle H=hAI_{z}J_{z}+{frac {hA}{2}}(J_{+}I_{-}+J_{-}I_{+})+mu _{rm {B}}Bg_{J}J_{z}+mu _{rm {N}}Bg_{I}I_{z}}

Ahora podemos ver que en todo momento, la proyección total del impulso angular $m_F = m_J + m_I$ se conservará. Esto es porque ambos $J_{z}$ y $I_z$ estados de licencia definidos ${displaystyle m_{J}}$ y ${displaystyle m_{I}}$ sin cambios, mientras ${displaystyle J_{+}I_{-}}$ y ${displaystyle J_{-}I_{+}}$ o aumento ${displaystyle m_{J}}$ y disminución ${displaystyle m_{I}}$ o viceversa, así que la suma no se ve afectada. Además, desde entonces $J = 1/2$ sólo hay dos posibles valores $m_J$ que son $pm 1/2$ . Por lo tanto, por cada valor de ${displaystyle m_{F}}$ sólo hay dos estados posibles, y podemos definirlos como la base:

|pmrangle equiv |m_J = pm 1/2, m_I = m_F mp 1/2 rangle

Este par de estados es un sistema mecánico cuántico de dos niveles. Ahora podemos determinar los elementos de la matriz del hamiltoniano:

{displaystyle langle pm |H|pm rangle =-{frac {1}{4}}hA+mu _{rm {N}}Bg_{I}m_{F}pm {frac {1}{2}}(hAm_{F}+mu _{rm {B}}Bg_{J}-mu _{rm {N}}Bg_{I}))}

langle pm |H| mp rangle = frac{1}{2} hA sqrt{(I + 1/2)^2 - m_F^2}

Resolviendo los valores propios de esta matriz (como se puede hacer a mano; consulte Sistema mecánico cuántico de dos niveles, o más fácilmente, con un sistema de álgebra computacional) llegamos a los cambios de energía:

{displaystyle Delta E_{F=Ipm 1/2}=-{frac {hDelta W}{2(2I+1)}}+mu _{rm {N}}g_{I}m_{F}Bpm {frac {hDelta W}{2}}{sqrt {1+{frac {2m_{F}x}{I+1/2}}+x^{2}}}}

{displaystyle xequiv {frac {B(mu _{rm {B}}g_{J}-mu _{rm {N}}g_{I})}{hDelta W}}quad quad Delta W=Aleft(I+{frac {1}{2}}right)}

Donde $Delta W$ es la división (en unidades de Hz) entre dos subnivels hiperfinos en ausencia de campo magnético $B$ , $x$ se conoce como el parámetro de fuerza del campo (Nota: para ${displaystyle m_{F}=pm (I+1/2)}$ la expresión bajo la raíz cuadrada es un cuadrado exacto, por lo que el último término debe ser reemplazado por ${displaystyle +{frac {hDelta W}{2}}(1pm x)}$ ). Esta ecuación se conoce como Breit-Rabi formula y es útil para sistemas con un electron de valence en un $s$ () $J = 1/2$ ) nivel.

Note ese índice $F$ dentro $Delta E_{F=Ipm1/2}$ debe considerarse no como el impulso angular total del átomo, sino como impulso angular total. Es igual al impulso angular total sólo si $B=0$ eigenvectores correspondientes a diferentes eigenvalues del Hamiltonian son las superposiciones de estados con diferentes $F$ pero igual $m_F$ (las únicas excepciones son $|F=I+1/2,m_F=pm F rangle$ ).

Aplicaciones

Astrofísica

Efecto Zeeman en una línea espectral de mancha solar

George Ellery Hale fue el primero en notar el efecto Zeeman en los espectros solares, lo que indica la existencia de fuertes campos magnéticos en las manchas solares. Dichos campos pueden ser bastante altos, del orden de 0,1 tesla o más. Hoy en día, el efecto Zeeman se usa para producir magnetogramas que muestran la variación del campo magnético en el Sol.

Refrigeración por láser

El efecto Zeeman se utiliza en muchas aplicaciones de enfriamiento de láser, como una trampa magneto-óptica y el Zeeman más lento.

Acoplamiento de giro y movimientos orbitales mediado por la energía de Zeeman

La interacción de giro-orbito en cristales se atribuye generalmente al acoplamiento de matrices Pauli $vec{sigma}$ a impulso electron ${vec {k}}$ que existe incluso en ausencia de campo magnético ${vec {B}}$ . Sin embargo, en las condiciones del efecto Zeeman, cuando ${displaystyle {vec {B}}neq 0}$ , una interacción similar se puede lograr mediante el acoplamiento $vec{sigma}$ al electron coordinar ${vec {r}}$ a través de la espacialmente inhomogénea Zeeman Hamiltonian

{displaystyle H_{rm {Z}}={frac {1}{2}}({vec {B}}{hat {g}}{vec {sigma }})}

Donde ${{hat g}}$ es un Landé diezsorial g-factor y bien ${displaystyle {vec {B}}={vec {B}}({vec {r}})}$ o ${displaystyle {hat {g}}={hat {g}}({vec {r}})}$ , o ambos, dependen de la coordinación de electrones ${vec {r}}$ . Tal ${vec {r}}$ - Zeeman Hamiltonian dependiente ${displaystyle H_{rm {Z}}({vec {r}})}$ parejas electron spin $vec{sigma}$ al operador ${vec {r}}$ representando el movimiento orbital de electrones. Campo inhomogéneo ${displaystyle {vec {B}}({vec {r}})}$ puede ser un campo liso de fuentes externas o un campo magnético microscópico de oscilación rápida en antiferromagnetes. Acoplamiento de giro-orbito a través de campo macroscópicamente inhomogéneo ${displaystyle {vec {B}}({vec {r}})}$ de nanoimágenes se utiliza para el funcionamiento eléctrico de los giros electrones en puntos cuánticos a través de la resonancia de la columna eléctrica dipole, y los giros de conducción por campo eléctrico debido a inhomogénesis ${displaystyle {hat {g}}({vec {r}})}$ también se ha demostrado.

Otro

Los antiguos estándares de frecuencia de alta precisión, es decir, los relojes atómicos basados en la transición de estructura hiperfina, pueden requerir ajustes periódicos debido a la exposición a campos magnéticos. Esto se lleva a cabo midiendo el efecto Zeeman en niveles específicos de transición de la estructura hiperfina del elemento fuente (cesio) y aplicando un campo magnético de baja intensidad y precisión uniforme a dicha fuente, en un proceso conocido como desmagnetización.

Contenido relacionado

Más resultados...

Estado inicial () ${displaystyle n=2,l=1}$ ) ${displaystyle mid j,m_{j}rangle }$	Estado final () ${displaystyle n=1,l=0}$ ) ${displaystyle mid j,m_{j}rangle }$	Energy perturbation
${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle mp {frac {2}{3}}mu _{rm {B}}B}$
${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},mp {frac {1}{2}}rightrangle }$	${displaystyle pm {frac {4}{3}}mu _{rm {B}}B}$
${displaystyle left\|{frac {3}{2}},pm {frac {3}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle pm mu _{rm {B}}B}$
${displaystyle left\|{frac {3}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle mp {frac {1}{3}}mu _{rm {B}}B}$
${displaystyle left\|{frac {3}{2}},pm {frac {1}{2}}rightrangle }$	${displaystyle left\|{frac {1}{2}},mp {frac {1}{2}}rightrangle }$	${displaystyle pm {frac {5}{3}}mu _{rm {B}}B}$

Estado inicial () ${displaystyle n=2,l=1}$ ) ${displaystyle mid m_{l},m_{s}rangle }$	Energía inicial Perturbación	Estado final () ${displaystyle n=1,l=0}$ ) ${displaystyle mid m_{l},m_{s}rangle }$
${displaystyle left\|1,{frac {1}{2}}rightrangle }$	${displaystyle pm 2mu _{rm {B}}B_{z}}$	${displaystyle left\|0,{frac {1}{2}}rightrangle }$
${displaystyle left\|0,{frac {1}{2}}rightrangle }$	${displaystyle +mu _{rm {B}}B_{z}}$	${displaystyle left\|0,{frac {1}{2}}rightrangle }$
${displaystyle left\|1,-{frac {1}{2}}rightrangle }$	$0$	${displaystyle left\|0,-{frac {1}{2}}rightrangle }$
${displaystyle left\|-1,{frac {1}{2}}rightrangle }$	$0$	${displaystyle left\|0,{frac {1}{2}}rightrangle }$
${displaystyle left\|0,-{frac {1}{2}}rightrangle }$	${displaystyle -mu _{rm {B}}B_{z}}$	${displaystyle left\|0,-{frac {1}{2}}rightrangle }$
${displaystyle left\|-1,-{frac {1}{2}}rightrangle }$	${displaystyle -2mu _{rm {B}}B_{z}}$	${displaystyle left\|0,-{frac {1}{2}}rightrangle }$

Efecto zeeman

Nomenclatura

Presentación teórica

Campo débil (efecto Zeeman)

Ejemplo: transición Lyman-alfa en hidrógeno

Campo fuerte (efecto Paschen-Back)

Campo intermedio para j = 1/2

Aplicaciones

Astrofísica

Refrigeración por láser

Acoplamiento de giro y movimientos orbitales mediado por la energía de Zeeman

Otro

Contenido relacionado

Zona fresnel

Edmond Halley

Nucleosíntesis