Efecto termoeléctrico

El efecto termoeléctrico es la conversión directa de diferencias de temperatura en voltaje eléctrico y viceversa a través de un termopar. Un dispositivo termoeléctrico crea un voltaje cuando hay una temperatura diferente en cada lado. Por el contrario, cuando se le aplica voltaje, el calor se transfiere de un lado al otro, creando una diferencia de temperatura. A escala atómica, un gradiente de temperatura aplicado hace que los portadores de carga en el material se difundan desde el lado caliente hacia el lado frío.

Este efecto se puede utilizar para generar electricidad, medir la temperatura o cambiar la temperatura de los objetos. Debido a que la dirección de calentamiento y enfriamiento se ve afectada por el voltaje aplicado, los dispositivos termoeléctricos se pueden utilizar como controladores de temperatura.

El término "efecto termoeléctrico" abarca tres efectos identificados por separado: el efecto Seebeck, el efecto Peltier y el efecto Thomson. Los efectos Seebeck y Peltier son manifestaciones diferentes de un mismo proceso físico; Los libros de texto pueden referirse a este proceso como el efecto Peltier-Seebeck (la separación se deriva de los descubrimientos independientes del físico francés Jean Charles Athanase Peltier y el físico alemán del Báltico Thomas Johann Seebeck). El efecto Thomson es una extensión del modelo Peltier-Seebeck y se le atribuye a Lord Kelvin.

El calentamiento Joule, el calor que se genera cada vez que una corriente pasa a través de un material conductor, generalmente no se denomina efecto termoeléctrico. Los efectos Peltier-Seebeck y Thomson son termodinámicamente reversibles, mientras que el calentamiento Joule no lo es.

Efecto Seebeck

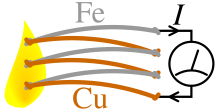
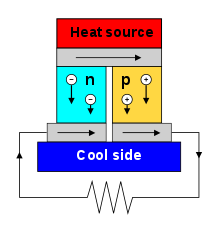
El efecto Seebeck es la fuerza electromotriz (fem) que se desarrolla a través de dos puntos de un material conductor de electricidad cuando hay una diferencia de temperatura entre ellos. La fem se llama fem de Seebeck (o fem termo/térmica/termoeléctrica). La relación entre la fem y la diferencia de temperatura es el coeficiente de Seebeck. Un termopar mide la diferencia de potencial entre un extremo frío y uno caliente para dos materiales diferentes. Esta diferencia de potencial es proporcional a la diferencia de temperatura entre los extremos frío y caliente. Descubierto por primera vez en 1794 por el científico italiano Alessandro Volta, lleva el nombre del físico alemán báltico Thomas Johann Seebeck, quien en 1821 lo redescubrió de forma independiente.

Seebeck observó lo que llamó "efecto termomagnético" en el que la aguja de una brújula magnética sería desviada por un bucle cerrado formado por dos metales diferentes unidos en dos lugares, con una diferencia de temperatura aplicada entre las uniones. El físico danés Hans Christian Ørsted observó que la diferencia de temperatura impulsaba en realidad una corriente eléctrica, siendo la generación de un campo magnético una consecuencia indirecta, por lo que acuñó el término más preciso "termoelectricidad".

El efecto Seebeck es un ejemplo clásico de fuerza electromotriz (EMF) y conduce a corrientes o voltajes medibles de la misma manera que cualquier otro EMF. La densidad de corriente local está dada por

J=σ σ ()− − Silencio Silencio V+Eemf),{displaystyle mathbf {J} =sigma (-nabla V+mathbf {E} _{text{emf}}}}}

Donde V{displaystyle V} es el voltaje local, y σ σ {displaystyle sigma } es la conductividad local. En general, el efecto Seebeck se describe localmente por la creación de un campo electromotivo

Eemf=− − SSilencio Silencio T,{displaystyle mathbf {E} {text{emf}=-Snabla T,}

Donde S{displaystyle S. es el coeficiente Seebeck (también conocido como termopoder), una propiedad del material local, y Silencio Silencio T{displaystyle nabla T} es el gradiente de temperatura.

Los coeficientes de Seebeck generalmente varían en función de la temperatura y dependen en gran medida de la composición del conductor. Para materiales ordinarios a temperatura ambiente, el valor del coeficiente de Seebeck puede variar entre −100 μV/K y +1000 μV/K (consulte el artículo sobre el coeficiente de Seebeck para obtener más información).

Aplicaciones

En la práctica, los efectos termoeléctricos son esencialmente inobservables para un punto frío o caliente localizado en un único material conductor homogéneo, ya que las fem generales de los gradientes de temperatura crecientes y decrecientes se cancelarán perfectamente. Conectar un electrodo al punto de acceso en un intento de medir el voltaje desplazado localmente solo tendrá un éxito parcial: significa que aparecerá otro gradiente de temperatura dentro del electrodo, por lo que la fem general dependerá de la diferencia en los coeficientes de Seebeck entre el electrodo y el conductor al que está conectado.

Los termopares implican dos cables, cada uno de un material diferente, que se unen eléctricamente en una región de temperatura desconocida. Los cabos sueltos se miden en un estado de circuito abierto (sin ninguna corriente, J=0{displaystyle mathbf {J} =0}). Aunque los materiales' Seebeck coefficents S{displaystyle S. son dependientes de temperatura no lineal y diferentes para los dos materiales, la condición de circuito abierto significa que Silencio Silencio V=− − SSilencio Silencio T{displaystyle nabla V=-Snabla T} Por todas partes. Por lo tanto (ver el artículo termopar para más detalles) el voltaje medido en los cabos sueltos de los alambres depende directamente de la temperatura desconocida, y sin embargo totalmente independiente de otros detalles como la geometría exacta de los alambres. Esta relación directa permite que el arreglo termopar sea utilizado como un termómetro sin calibrar directo, siempre que se conozca la diferencia en S{displaystyle S.-vs...T{displaystyle T} curvas de los dos materiales, y de la temperatura de referencia en los extremos de alambre suelto medidos.

Funciones de clasificación termoeléctrica similares a un termopar pero implica un material desconocido en lugar de una temperatura desconocida: una sonda metálica de composición conocida se mantiene a una temperatura constante conocida y se mantiene en contacto con la muestra desconocida que se calienta localmente a la temperatura de la sonda, proporcionando así una medición aproximada del coeficiente de Seebeck desconocido S{displaystyle S.. Esto puede ayudar a distinguir entre diferentes metales y aleaciones.

Las termopilas se forman a partir de muchos termopares en serie, zigzagueando hacia adelante y hacia atrás entre frío y calor. Esto multiplica la salida de voltaje.

Los generadores termoeléctricos son como un termopar/termopila, pero en su lugar extraen algo de corriente del voltaje generado para extraer energía de los diferenciales de calor. Están optimizados de manera diferente a los termopares, utilizando materiales termoeléctricos de alta calidad en una disposición de termopila, para maximizar la potencia extraída. Aunque no son particularmente eficientes, estos generadores tienen la ventaja de no tener partes móviles.

Efecto Peltier

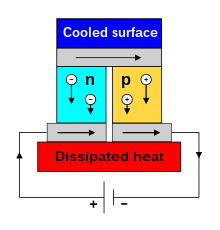
Cuando una corriente eléctrica pasa a través del circuito de un termopar, se genera calor en una unión y se absorbe en la otra unión. Esto se conoce como efecto Peltier: la presencia de calentamiento o enfriamiento en una unión electrificada de dos conductores diferentes. El efecto lleva el nombre del físico francés Jean Charles Athanase Peltier, quien lo descubrió en 1834. Cuando se hace fluir una corriente a través de una unión entre dos conductores, A y B, se puede generar o eliminar calor en la unión. El calor Peltier generado en la unión por unidad de tiempo es

QÍ Í =()▪ ▪ A− − ▪ ▪ B)I,Yo...

Donde ▪ ▪ A{displaystyle "Pi" y ▪ ▪ B{displaystyle "Pi" son los coeficientes Peltier de los conductores A y B, y I{displaystyle Yo... es la corriente eléctrica (de A a B). El calor total generado no está determinado por el efecto Peltier solo, ya que también puede ser influenciado por el calentamiento Joule y los efectos de grado térmico (ver abajo).

Los coeficientes Peltier representan cuánto calor se carga por unidad. Puesto que la corriente de carga debe ser continua a través de una unión, el flujo de calor asociado desarrollará una discontinuidad si ▪ ▪ A{displaystyle "Pi" y ▪ ▪ B{displaystyle "Pi" son diferentes. El efecto Peltier se puede considerar como el contraparte de acción posterior al efecto Seebeck (análogo a la parte posterior del EEMF en la inducción magnética): si un simple circuito termoeléctrico está cerrado, entonces el efecto Seebeck conducirá una corriente, que a su vez (por el efecto Peltier) siempre transferirá el calor del calor a la unión fría. La estrecha relación entre los efectos de Peltier y Seebeck se puede ver en la conexión directa entre sus coeficientes: ▪ ▪ =TS{displaystyle Pi =TS} (véase infra).

Una bomba de calor Peltier típica implica múltiples uniones en serie, a través de las cuales se conduce una corriente. Algunas de las uniones pierden calor debido al efecto Peltier, mientras que otras ganan calor. Las bombas de calor termoeléctricas aprovechan este fenómeno, al igual que los dispositivos de refrigeración termoeléctricos que se encuentran en los refrigeradores.

Aplicaciones

El efecto Peltier se puede utilizar para crear una bomba de calor. En particular, el refrigerador termoeléctrico Peltier es un refrigerador compacto y sin fluido circulante ni partes móviles. Estos refrigeradores son útiles en aplicaciones en las que sus ventajas superan la desventaja de su muy baja eficiencia.

Otras aplicaciones de bombas de calor, como los deshumidificadores, también pueden utilizar bombas de calor Peltier.

Los refrigeradores termoeléctricos son trivialmente reversibles, ya que pueden usarse como calentadores simplemente invirtiendo la corriente. A diferencia del calentamiento eléctrico resistivo ordinario (calentamiento Joule) que varía con el cuadrado de la corriente, el efecto de calentamiento termoeléctrico es lineal en corriente (al menos para corrientes pequeñas) pero requiere un sumidero frío para reponerse con energía térmica. Este efecto de calentamiento y enfriamiento de rápida inversión es utilizado por muchos termocicladores modernos, dispositivos de laboratorio utilizados para amplificar el ADN mediante la reacción en cadena de la polimerasa (PCR). La PCR requiere el calentamiento y enfriamiento cíclicos de las muestras a temperaturas específicas. La inclusión de muchos termopares en un espacio pequeño permite amplificar muchas muestras en paralelo.

Efecto Thomson

En diferentes materiales, el coeficiente Seebeck no es constante en temperatura, por lo que un gradiente espacial en temperatura puede resultar en un gradiente en el coeficiente Seebeck. Si una corriente es impulsada a través de este gradiente, entonces se producirá una versión continua del efecto Peltier. Esto Efecto Thomson fue predicho y posteriormente observado en 1851 por el Señor Kelvin (William Thomson). Describe el calentamiento o enfriamiento de un conductor de carga actual con un gradiente de temperatura. Si una densidad actual J{displaystyle mathbf {J} se pasa a través de un conductor homogéneo, el efecto Thomson predice una tasa de producción de calor por volumen de unidad.

qÍ Í =− − KJ⋅ ⋅ Silencio Silencio T,{displaystyle { dot {}=-{mathcal {K}Mathbf {J} cdot nabla T,}

Donde Silencio Silencio T{displaystyle nabla T} es la temperatura gradiente, y K{displaystyle {fnMithcal}} es el coeficiente de Thomson. El efecto Thomson es una manifestación de la dirección del flujo de los transportistas eléctricos con respecto a un gradiente de temperatura dentro de un conductor. Estos absorben energía (calor) fluyendo en una dirección opuesta a un gradiente térmico, aumentando su energía potencial, y, al fluir en la misma dirección que un gradiente térmico, liberan el calor, disminuyendo su energía potencial. El coeficiente Thomson está relacionado con el coeficiente Seebeck como K=TdSdT{displaystyle {fnMitcal}=T{tfrac {dS} {dT}} (véase infra). Esta ecuación, sin embargo, descuida la calefacción Joule y la conductividad térmica ordinaria (ver ecuaciones completas abajo).

Ecuaciones termoeléctricas completas

A menudo, más de uno de los efectos anteriores está involucrado en el funcionamiento de un dispositivo termoeléctrico real. El efecto Seebeck, el efecto Peltier y el efecto Thomson se pueden reunir de manera consistente y rigurosa, como se describe aquí; esto también incluye los efectos del calentamiento Joule y la conducción de calor ordinaria. Como se indicó anteriormente, el efecto Seebeck genera una fuerza electromotriz, lo que lleva a la ecuación actual

J=σ σ ()− − Silencio Silencio V− − SSilencio Silencio T).{displaystyle mathbf {J} =sigma (-{boldsymbol {nabla) }V-Snabla T).}

Para describir los efectos Peltier y Thomson, debemos considerar el flujo de energía. Si la temperatura y la carga cambian con el tiempo, la ecuación termoeléctrica completa para la acumulación de energía, eÍ Í {displaystyle { dot {e}}, es

eÍ Í =Silencio Silencio ⋅ ⋅ ()κ κ Silencio Silencio T)− − Silencio Silencio ⋅ ⋅ ()V+▪ ▪ )J+qÍ Í ext,{kappa nabla T)-nabla cdot (V+Pi)mathbf {J} +{dot {q}_{text{ext}}}

Donde κ κ {displaystyle kappa } es la conductividad térmica. El primer término es la ley de conducción de calor de Fourier, y el segundo término muestra la energía transportada por corrientes. El tercer mandato, qÍ Í ext{displaystyle {dot {fnK}} {text{ext}}}, es el calor añadido de una fuente externa (si es aplicable).

Si el material ha alcanzado un estado estable, las distribuciones de carga y temperatura son estables, por lo que eÍ Í =0{displaystyle { dot {}=0} y Silencio Silencio ⋅ ⋅ J=0{displaystyle nabla cdot mathbf {J} =0}. Utilizando estos hechos y la segunda relación Thomson (ver abajo), la ecuación de calor puede ser simplificada

− − qÍ Í ext=Silencio Silencio ⋅ ⋅ ()κ κ Silencio Silencio T)+J⋅ ⋅ ()σ σ − − 1J)− − TJ⋅ ⋅ Silencio Silencio S.{displaystyle -{dot {}_{text{ext}=nabla cdot (kappa nabla T)+mathbf {J} cdot left(sigma ^{-1}mathbf {J}right)-Tmathbf {J} cdot nabla S}}

El término medio es la calefacción Joule, y el último término incluye a Peltier (Silencio Silencio S{displaystyle nabla S} en la unión) y Thomson (Silencio Silencio S{displaystyle nabla S} en el gradiente térmico) efectos. Combinado con la ecuación Seebeck para J{displaystyle mathbf {J}, esto se puede utilizar para resolver para los perfiles de tensión y temperatura estable en un sistema complicado.

Si el material no está en estado estable, una descripción completa debe incluir efectos dinámicos como los relacionados con la capacitancia eléctrica, la inductancia y la capacidad calorífica.

Los efectos termoeléctricos se encuentran más allá del alcance de la termodinámica de equilibrio. Implican necesariamente flujos continuos de energía. Se trata, al menos, de tres cuerpos o subsistemas termodinámicos, dispuestos de una manera particular, junto con una disposición especial del entorno. Los tres cuerpos son los dos metales diferentes y su región de unión. La región de unión es un cuerpo no homogéneo, que se supone estable y que no sufre fusión por difusión de materia. Los alrededores están dispuestos para mantener dos depósitos de temperatura y dos depósitos eléctricos.

Para un equilibrio termodinámico imaginado, pero no posible en realidad, la transferencia de calor del depósito caliente al depósito frío debería evitarse mediante una diferencia de voltaje específicamente coincidente mantenida por los depósitos eléctricos, y la corriente eléctrica tendría que ser cero. Para un estado estable, debe haber al menos cierta transferencia de calor o alguna corriente eléctrica distinta de cero. Los dos modos de transferencia de energía, como calor y corriente eléctrica, se pueden distinguir cuando hay tres cuerpos distintos y una disposición distinta de los alrededores.

Pero en el caso de una variación continua en los medios, la transferencia de calor y el trabajo termodinámico no pueden distinguirse de manera única. Esto es más complicado que los procesos termodinámicos que a menudo se consideran, en los que sólo están conectados dos subsistemas respectivamente homogéneos.

Relaciones de Thomson

En 1854, Lord Kelvin encontró relaciones entre los tres coeficientes, lo que implica que los efectos Thomson, Peltier y Seebeck son manifestaciones diferentes de un efecto (caracterizado exclusivamente por el coeficiente de Seebeck).

La primera relación de Thomson es

K↑ ↑ d▪ ▪ dT− − S,{displaystyle {fnMithcal}equiv} {fnMicroc} - Sí.

Donde T{displaystyle T} es la temperatura absoluta, K{displaystyle {fnMithcal}} es el coeficiente de Thomson, ▪ ▪ {displaystyle Pi } es el coeficiente Peltier, y S{displaystyle S. es el coeficiente Seebeck. Esta relación se muestra fácilmente dado que el efecto Thomson es una versión continua del efecto Peltier.

La segunda relación de Thomson es

▪ ▪ =TS.{displaystyle Pi =TS.}

Esta relación expresa una conexión sutil y fundamental entre los efectos Peltier y Seebeck. No se demostró satisfactoriamente hasta el advenimiento de las relaciones de Onsager, y vale la pena señalar que esta segunda relación de Thomson sólo está garantizada para un material simétrico de inversión temporal; si el material se coloca en un campo magnético o está él mismo ordenado magnéticamente (ferromagnético, antiferromagnético, etc.), entonces la segunda relación de Thomson no toma la forma simple que se muestra aquí.

Ahora, usando la segunda relación, la primera relación de Thomson se convierte en

K=TdSdT{displaystyle {fnMitcal}=T{tfrac {dS} {dT}}

El coeficiente de Thomson es único entre los tres coeficientes termoeléctricos principales porque es el único que se puede medir directamente para materiales individuales. Los coeficientes de Peltier y Seebeck sólo pueden determinarse fácilmente para pares de materiales; por lo tanto, es difícil encontrar valores de los coeficientes absolutos de Seebeck o Peltier para un material individual.

Si el coeficiente de Thomson de un material se mide en un amplio rango de temperaturas, se puede integrar utilizando las relaciones de Thomson para determinar los valores absolutos de los coeficientes de Peltier y Seebeck. Esto debe hacerse solo para un material, ya que los otros valores se pueden determinar midiendo los coeficientes de Seebeck por pares en termopares que contienen el material de referencia y luego sumando nuevamente el coeficiente de Seebeck absoluto del material de referencia. Para obtener más detalles sobre la determinación del coeficiente de Seebeck absoluto, consulte Coeficiente de Seebeck.