Efecto Overhauser nuclear

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Efecto de espectroscopia de resonancia magnética nuclear

El efecto Overhauser nuclear (NOE) es la transferencia de la polarización del espín nuclear de una población de núcleos con espín activo (por ejemplo, ¹H, ¹³C, ¹⁵N, etc.) a otro mediante relajación cruzada. Una definición fenomenológica de NOE en la espectroscopia de resonancia magnética nuclear (RMN) es el cambio en la intensidad integrada (positiva o negativa) de una resonancia de RMN que se produce cuando otra se satura por irradiación con un campo de RF. El cambio en la intensidad de resonancia de un núcleo es consecuencia de que el núcleo está cerca en el espacio de aquellos directamente afectados por la perturbación de RF.

La NOE es particularmente importante en la asignación de resonancias RMN, y la elucidación y confirmación de las estructuras o configuraciones de moléculas orgánicas y biológicas. El experimento de espectroscopia NOE bidimensional de ¹H (NOESY) y sus extensiones son herramientas importantes para identificar la estereoquímica de proteínas y otras biomoléculas en solución, mientras que la difracción de rayos X de cristal en forma sólida se suele utilizar para identificar la estereoquímica.. El NOE heteronuclear es particularmente importante en la espectroscopia de RMN de ¹³C para identificar carbonos unidos a protones, proporcionar mejoras de polarización a dichos carbonos para aumentar la relación señal-ruido y determinar el grado de relajación de estos carbonos. está controlado por el mecanismo de relajación dipolo-dipolo.

Historia

La NOE se desarrolló a partir del trabajo teórico del físico estadounidense Albert Overhauser, quien en 1953 propuso que la polarización del espín nuclear podría mejorarse mediante la irradiación de microondas de los electrones de conducción en ciertos rieles. La mejora electronuclear predicha por Overhauser fue demostrada experimentalmente en ⁷Li metal por T. R. Carver y C. P. Slichter también en 1953. Ionel Solomon publicó en 1955 una base teórica general y una observación experimental de un efecto Overhauser que involucra solo espines nucleares en la molécula de HF. Kaiser utilizó otra observación experimental temprana del NOE en 1963 para mostrar cómo el NOE se puede utilizar para determinar los signos relativos de constantes de acoplamiento escalares y para asignar líneas espectrales en espectros de RMN a transiciones entre niveles de energía. En este estudio, la resonancia de una población de protones (¹H) en una molécula orgánica se mejoró cuando una segunda población distinta de protones en la misma molécula orgánica se saturó con radiación de RF. La aplicación de NOE fue utilizada por Anet y Bourn en 1965 para confirmar las asignaciones de las resonancias de RMN para el ácido β, β-dimetilacrílico y la dimetilformamida, lo que demuestra que se puede obtener información sobre la conformación y configuración de moléculas orgánicas en solución. Bell y Saunders informaron una correlación directa entre las mejoras de NOE y las distancias internucleares en 1970, mientras que Schirmer et al informaron mediciones cuantitativas de distancias internucleares en moléculas con tres o más espines.

Richard R. Ernst recibió el Premio Nobel de Química en 1991 por desarrollar la transformada de Fourier y la espectroscopia de RMN bidimensional, que pronto se adaptó a la medición de la NOE, especialmente en moléculas biológicas grandes. En 2002, Kurt Wuthrich ganó el Premio Nobel de Química por el desarrollo de la espectroscopia de resonancia magnética nuclear para determinar la estructura tridimensional de macromoléculas biológicas en solución, demostrando cómo se puede utilizar el método 2D NOE (NOESY) para restringir la estructura tridimensional. estructuras de grandes macromoléculas biológicas. El profesor Anil Kumar fue el primero en aplicar el experimento del efecto Overhauser nuclear bidimensional (2D-NOE ahora conocido como NOESY) a una biomolécula, lo que abrió el campo para la determinación de estructuras tridimensionales de biomoléculas en solución mediante espectroscopia de RMN.

Relajación

La NOE y la relajación de la red de espín nuclear son fenómenos estrechamente relacionados. Para un solo núcleo de spin-1⁄2 en un campo magnético hay dos niveles de energía que a menudo se denominan α y β, que corresponden a los dos posibles estados cuánticos de espín, +1 ⁄2 y -1 ⁄2, respectivamente. En equilibrio térmico, la población de los dos niveles de energía está determinada por la distribución de Boltzmann con poblaciones de espín dadas por P_α y P_β. Si las poblaciones de espín son perturbadas por un campo de RF apropiado en la frecuencia de energía de transición, las poblaciones de espín vuelven al equilibrio térmico mediante un proceso llamado relajación de red de espín. La tasa de transiciones de α a β es proporcional a la población del estado α, P_α, y es un proceso de primer orden con constante de tasa W. La condición en la que las poblaciones de espín se igualan mediante irradiación de RF continua (P_α = P_β) se llama saturación y la resonancia desaparece ya que las probabilidades de transición dependen de la diferencia de población entre los niveles de energía.

En el caso más simple donde el NOE es relevante, las resonancias de dos spin-1⁄2, I y S, están químicamente desplazados pero no acoplados en forma de J. El diagrama de energía para tal sistema tiene cuatro niveles de energía que dependen de los estados de espín de I y S correspondientes a αα, αβ, βα y ββ, respectivamente. Los W' son las probabilidades por unidad de tiempo de que ocurra una transición entre los cuatro niveles de energía o, en otros términos, la velocidad a la que se producen los giros correspondientes. Hay dos transiciones cuánticas simples, W₁^I, correspondientes a αα ➞ βα y αβ ➞ ββ; W₁^S, correspondiente a αα ➞ αβ y βα ➞ ββ; una transición cuántica cero, W₀, correspondiente a βα ➞ αβ, y una transición cuántica doble correspondiente a αα ➞ ββ.

Mientras que la radiación de radiofrecuencia solo puede inducir transiciones de un solo cuanto (debido a las llamadas reglas de selección de la mecánica cuántica) que dan lugar a líneas espectrales observables, la relajación dipolar puede tener lugar a través de cualquiera de las vías. El mecanismo dipolar es el único mecanismo de relajación común que puede causar transiciones en las que se invierte más de un espín. En concreto, el mecanismo de relajación dipolar da lugar a transiciones entre los estados αα y ββ (W₂) y entre los estados αβ y βα (W₀).

Expresado en términos de sus magnetizaciones NMR a granel, el NOE de estado estable observado experimentalmente para el núcleo I cuando la resonancia del núcleo S está saturada ( ${displaystyle M_{S}=0}$ ) se define por la expresión:

{displaystyle eta _{I}^{S}=left({frac {M_{I}^{S}-M_{0I}}{M_{0I}}}right)}

Donde ${displaystyle M_{0I}}$ es la magnetización (intensidad de la resonancia) del núcleo $I$ en equilibrio térmico. Una expresión analítica para el NOE se puede obtener considerando todas las vías de relajación y aplicando las ecuaciones Salomón para obtener

{displaystyle eta _{I}^{S}={frac {M_{I}^{S}-M_{0I}}{M_{0I}}}={frac {gamma _{S}}{gamma _{I}}}{frac {sigma _{IS}}{rho _{I}}}={frac {gamma _{S}}{gamma _{I}}}left({frac {W_{2}-W_{0}}{2W_{1}^{I}+W_{0}+W_{2}}}right)}

dónde

{displaystyle rho _{I}=2W_{1}^{I}+W_{0}+W_{2}}

{displaystyle sigma _{IS}=W_{2}-W_{0}}

${displaystyle rho _{I}}$ es la tasa total de relajación dipolar longitudinal ( ${displaystyle 1/T_{1}}$ ) de la vuelta I debido a la presencia de la columna s, ${displaystyle sigma _{IS}}$ se conoce como el cross-relaxation y ${displaystyle gamma _{I}}$ y ${displaystyle gamma _{S}}$ son las ratios magnetogyric características de la $I$ y $S$ nuclei, respectivamente.

Saturación del degenerado W₁^S transiciones perturban las poblaciones de equilibrio para que P_α = P_αβ y P_β = P_β. Las vías de relajación del sistema, sin embargo, permanecen activas y actúan para restablecer un equilibrio, excepto que el W₁^S las transiciones son irrelevantes porque las diferencias de población en estas transiciones están fijadas por la irradiación RF mientras que la diferencia de población entre la W_I las transiciones no cambian de sus valores de equilibrio. Esto significa que si sólo las únicas transiciones cuánticas estaban activas como vías de relajación, saturando las $S$ la resonancia no afectaría la intensidad de la $I$ resonancia. Por lo tanto, observar un NOE sobre la intensidad de resonancia de I, la contribución de ${displaystyle W_{0}}$ y ${displaystyle W_{2}}$ Debe ser importante. Estos caminos, conocidos como cross-relaxation caminos, sólo hacen una contribución significativa a la relajación de la tracción de la columna cuando la relajación está dominada por interacciones dipole-dipole o de acoplamiento escalar, pero la interacción escalar es raramente importante y se supone que es insignificante. En el caso homonuclear ${displaystyle gamma _{I}=gamma _{S}}$ , si ${displaystyle W_{2}}$ es el camino de relajación dominante, luego saturar $S$ aumenta la intensidad de la $I$ resonancia y el NOE es positivo, mientras que si $W_{0}$ es el camino de relajación dominante, saturando $S$ disminuye la intensidad de la $I$ resonancia y el NOE es negativo.

Movimiento molecular

Si el NOE es positivo o negativo depende sensiblemente del grado de movimiento molecular rotacional. Las tres vías de relajación dipolar contribuyen a diferentes grados a la relajación de la tracción de la columna dependiendo de varios factores. Una clave es que el equilibrio entre ω₂, ω₁ and ω₀ depende fundamentalmente del tiempo de correlación molecular rotacional, $tau_{c}$ , el tiempo que se necesita una molécula para girar un radio. La teoría de NMR muestra que las probabilidades de transición están relacionadas con $tau_{c}$ y las frecuencias de precesión de Larmor, $omega$ , por las relaciones:

{displaystyle W_{1}^{I}propto {frac {3tau _{c}}{(1+omega _{I}^{2}tau _{c}^{2})}}{frac {1}{r^{6}}}}

{displaystyle W_{0}propto {frac {2tau _{c}}{(1+(omega _{I}-omega _{S})^{2}tau _{c}^{2})}}{frac {1}{r^{6}}}}

{displaystyle W_{2}propto {frac {12tau _{c}}{(1+(omega _{I}+omega _{S})^{2}tau _{c}^{2})}}{frac {1}{r^{6}}}}

Donde $r$ es la distancia separando dos vueltas-1.2 nuclei. Para que se produzca la relajación, la frecuencia de tumbling molecular debe coincidir con la frecuencia Larmor del núcleo. En disolventes móviles, el movimiento de afinación molecular es mucho más rápido que $omega$ . El llamado límite de extrema derecha donde ${displaystyle omega tau _{c}ll 1}$ ). Bajo estas condiciones la relajación doble-cuántica W₂ es más eficaz que W₁ o W₀, porque τ_c and 2ω₀ partido mejor que τ_c and ω₁. When ω₂ es el proceso de relajación dominante, un resultado positivo NOE.

{displaystyle W_{1}^{I}propto gamma _{I}^{2}gamma _{S}^{2}{frac {3tau _{c}}{r^{6}}}}

{displaystyle W_{0}propto gamma _{I}^{2}gamma _{S}^{2}{frac {2tau _{c}}{r^{6}}}}

{displaystyle W_{2}propto gamma _{I}^{2}gamma _{S}^{2}{frac {12tau _{c}}{r^{6}}}}

{displaystyle eta _{I}^{S}(max)={frac {gamma _{S}}{gamma _{I}}}left[{frac {{frac {12tau _{c}}{r^{6}}}-{frac {2tau _{c}}{r^{6}}}}{{frac {2tau _{c}}{r^{6}}}+2{frac {3tau _{c}}{r^{6}}}+{frac {12tau _{c}}{r^{6}}}}}right]={frac {gamma _{S}}{gamma _{I}}}left[{frac {12-2}{2+6+12}}right]={frac {gamma _{S}}{gamma _{I}}}{frac {1}{2}}}

Esta expresión muestra que para el caso homonuclear donde I = S, más notablemente para ¹H RMN, el NOE máximo que se puede observar es 12 independientemente de la proximidad de los núcleos. En el caso heteronuclear donde I ≠ S, el NOE máximo viene dado por 12 (γ_S/ γ_I), que, al observar heteronúcleos en condiciones de desacoplamiento de protones de banda ancha, puede producir importantes mejoras de sensibilidad. El ejemplo más importante en química orgánica es la observación de ¹³C mientras se desacopla ¹H, que también satura las resonancias de ¹J. El valor de γ_S/γ_I es cercano a 4, lo que da una mejora máxima de NOE del 200% produciendo resonancias 3 veces más fuertes de lo que serían sin NOE. En muchos casos, los átomos de carbono tienen un protón adjunto, lo que hace que la relajación esté dominada por la relajación dipolar y que el NOE esté cerca del máximo. Para los átomos de carbono no protonados, la mejora de NOE es pequeña, mientras que para los carbonos que se relajan mediante mecanismos de relajación distintos de las interacciones dipolo-dipolo, la mejora de NOE puede reducirse significativamente. Esta es una de las motivaciones para usar disolventes deuterados (p. ej., CDCl3) en ¹³C RMN. Dado que el deuterio se relaja por el mecanismo cuadrupolar, no hay vías de relajación cruzada y NOE es inexistente. Otro caso importante es ¹⁵N, un ejemplo donde el valor de su relación magnetogira es negativo. A menudo, las resonancias de ¹⁵N se reducen o el NOE puede anular la resonancia cuando se desacoplan los núcleos de ¹H. Por lo general, es ventajoso tomar dichos espectros con técnicas de pulso que implican la transferencia de polarización de los protones al ¹⁵N para minimizar el NOE negativo.

Elucidación de la estructura

Si bien la relación del NOE en estado estacionario con la distancia internuclear es compleja, dependiendo de las tasas de relajación y el movimiento molecular, en muchos casos, para moléculas pequeñas que giran rápidamente en el límite de estrechamiento extremo, la naturaleza semicuantitativa del NOE' s es útil para muchas aplicaciones estructurales, a menudo en combinación con la medición de constantes de acoplamiento J. Por ejemplo, las mejoras de NOE se pueden usar para confirmar asignaciones de resonancia de RMN, distinguir entre isómeros estructurales, identificar patrones de sustitución de anillos aromáticos y configuraciones de sustituyentes alifáticos, y determinar preferencias conformacionales.

Sin embargo, las distancias interatómicas derivadas del NOE observado a menudo pueden ayudar a confirmar la estructura tridimensional de una molécula. En esta aplicación, el NOE difiere de la aplicación del acoplamiento J en que el NOE ocurre a través del espacio, no a través de enlaces químicos. Por lo tanto, los átomos que están muy cerca unos de otros pueden dar un NOE, mientras que el acoplamiento de espín se observa solo cuando los átomos están conectados por 2 o 3 enlaces químicos. Sin embargo, la relación η_I^S(max)=1⁄2 oscurece cómo el NOE se relaciona con las distancias internucleares porque solo se aplica al caso ideal en el que la relajación está dominada al 100 %. por interacciones dipolo-dipolo entre dos núcleos I y S. En la práctica, el valor de ρ_I contiene contribuciones de otros mecanismos en competencia, que sirven solo para reducir la influencia de W ₀ y W₂ aumentando W₁. A veces, por ejemplo, la relajación debida a interacciones electrón-nucleares con oxígeno disuelto o impurezas de iones metálicos paramagnéticos en el solvente puede prohibir la observación de aumentos débiles de NOE. El NOE observado en presencia de otros mecanismos de relajación viene dado por

{displaystyle eta _{I}={frac {sigma _{IS}}{rho _{I}+rho ^{*}}}}

donde ρ^⋇ es la contribución adicional a la tasa de relajación total de los mecanismos de relajación que no involucran relajación cruzada. Usando el mismo modelo idealizado de dos giros para la relajación dipolar en el límite de estrechamiento extremo:

{displaystyle rho _{I}propto {frac {tau _{c}}{r^{6}}}}

Es fácil demostrar que

{displaystyle eta _{I}^{S}propto left({frac {tau _{c}}{rho ^{*}}}right){frac {1}{r^{6}}}}

Por lo tanto, el NOE de estado estacionario de dos espín depende de la distancia internuclear solo cuando hay una contribución de la relajación externa. Bell y Saunders demostraron que, siguiendo suposiciones estrictas, ρ^⋇/τ_c es casi constante para moléculas similares en el límite de estrechamiento extremo. Por lo tanto, tomar proporciones de valores de NOE en estado estacionario puede dar valores relativos para la distancia internuclear r. Si bien el experimento de estado estacionario es útil en muchos casos, solo puede proporcionar información sobre distancias internucleares relativas. Por otro lado, la tasa inicial a la que crece el NOE es proporcional a r_IS⁻⁶, que proporciona otras alternativas más sofisticadas para obtener información estructural a través de experimentos transitorios como 2D-NOESY.

RMN bidimensional

Las motivaciones para usar RMN bidimensional para medir los NOE son similares a las de otros métodos 2D. La resolución máxima se mejora al distribuir las resonancias afectadas en dos dimensiones, por lo tanto, se resuelven más picos, se pueden observar moléculas más grandes y se pueden observar más NOE en una sola medición. Más importante aún, cuando el movimiento molecular está en los regímenes de movimiento intermedio o lento cuando el NOE es cero o negativo, el experimento NOE en estado estacionario no brinda resultados que puedan relacionarse con las distancias internucleares.

La espectroscopia de efecto Overhauser nuclear (NOESY) es un método espectroscópico de RMN 2D que se utiliza para identificar espines nucleares que experimentan relajación cruzada y para medir sus tasas de relajación cruzada. Dado que los acoplamientos dipolo-dipolo de ¹H proporcionan el medio principal de relajación cruzada para las moléculas orgánicas en solución, los espines que experimentan relajación cruzada son aquellos que están cerca unos de otros en el espacio. Por lo tanto, los picos cruzados de un espectro NOESY indican qué protones están cerca unos de otros en el espacio. En este sentido, el experimento NOESY difiere del experimento COSY en que se basa en el acoplamiento J para proporcionar una correlación espín-espín, y cuyos picos cruzados indican qué ¹H's están cerca de qué otras ¹H's a través de los enlaces químicos de la molécula.

La secuencia básica de NOESY consta de tres pulsos de 90°. El primer pulso crea una magnetización de espín transversal. Los espines precesan durante el tiempo de evolución t₁, que se incrementa durante el transcurso del experimento 2D. El segundo pulso produce una magnetización longitudinal igual a la componente de magnetización transversal ortogonal a la dirección del pulso. Por lo tanto, la idea es producir una condición inicial para el período de mezcla τ_m. Durante el tiempo de mezcla de NOE, puede tener lugar la transferencia de magnetización mediante relajación cruzada. Para el experimento NOESY básico, τ_m se mantiene constante a lo largo del experimento 2D, pero se elige para la tasa óptima de relajación cruzada y la acumulación de NOE. El tercer pulso crea magnetización transversal a partir de la magnetización longitudinal restante. La adquisición de datos comienza inmediatamente después del tercer pulso y se observa la magnetización transversal en función del tiempo de retardo del pulso t₂. El espectro NOESY se genera mediante una transformada de Fourier 2D con respecto a t₁ y t₂. Se lleva a cabo una serie de experimentos con tiempos de mezclado crecientes y se sigue el aumento en la mejora de NOE. Los protones más cercanos muestran las tasas de acumulación más rápidas del NOE.

Las distancias entre protones pueden determinarse a partir de espectros NOESY sin ambigüedades, bien resueltos y de alta señal a ruido mediante el análisis de intensidades pico cruzadas. Estos pueden obtenerse mediante la integración del volumen y pueden convertirse en estimaciones de distancias interprotonas. La distancia entre dos átomos $i$ y $j$ se puede calcular a partir de los volúmenes de pico cruzado $V$ y una constante de escalada $c$

{displaystyle r_{text{NOE}}=left({frac {c}{V_{ij}}}right)^{1/6}}

Donde $c$ puede determinarse sobre la base de mediciones de distancias fijas conocidas. El rango de distancias puede ser reportado basado en distancias y volúmenes conocidos en el espectro, lo que da una media $c$ y una desviación estándar ${displaystyle c_{SD}}$ , una medición de múltiples regiones en el espectro NOESY sin picos, i.e. ruido ${displaystyle V_{rm {err}}}$ , y un error de medición $m_v$ . El parámetro $x$ se establece para que todas las distancias conocidas estén dentro de los límites de error. Esto muestra que el rango inferior del volumen NOESY se puede mostrar

{displaystyle r_{text{NOE lower}}=left({frac {c-xc_{SD}}{{frac {1}{m_{v}}}V_{ij}+V_{rm {err}}}}right)^{1/6}}

y que el límite superior es

{displaystyle r_{text{NOE higher}}=left({frac {c+xc_{SD}}{{frac {1}{m_{v}}}V_{ij}-V_{rm {err}}}}right)^{1/6}}

Tales distancias fijas dependen del sistema estudiado. Por ejemplo, los ácidos nucleicos bloqueados tienen muchos átomos cuya distancia varía muy poco en el azúcar, lo que permite la estimación de los ángulos de torsión glucosídicos, lo que permitió a la RMN comparar las predicciones de la dinámica molecular del LNA. Los ARN, sin embargo, tienen azúcares que son mucho más flexibles conformacionalmente y requieren estimaciones más amplias de límites bajos y altos.

En la caracterización estructural de proteínas, los NOE se utilizan para crear restricciones en las distancias intramoleculares. En este método, cada par de protones se considera de forma aislada y las intensidades de los picos cruzados de NOESY se comparan con un pico cruzado de referencia de un par de protones de distancia fija, como un par de protones de metileno geminal o protones de anillo aromático. Este enfoque simple es razonablemente insensible a los efectos de la difusión del espín o los tiempos de correlación no uniformes y, por lo general, puede conducir a la definición del pliegue global de la proteína, siempre que se haya identificado un número suficientemente grande de NOE. Los picos cruzados de NOESY se pueden clasificar como fuertes, medios o débiles y se pueden traducir en restricciones de distancia superior de alrededor de 2,5, 3,5 y 5,0 Å, respectivamente. Estas restricciones se pueden usar en optimizaciones de mecánica molecular para proporcionar una imagen de la conformación del estado de solución de la proteína. La determinación de la estructura completa se basa en una variedad de experimentos de RMN y métodos de optimización que utilizan restricciones de cambio químico y NOESY.

NOE heteronuclear

Algunos métodos experimentales

Algunos ejemplos de técnicas experimentales de RMN unidimensional y bidimensional que aprovechan el NOE incluyen:

NOESY, Efecto de sobrehausto nuclear Espectroscopia
HOESY, Heteronuclear Espectroscopia de efecto overhauser
ROESY, Rotational frame nuclear Espectroscopia de efecto overhauser
TRNOE, Transferred nuclear Efecto del agotamiento
DPFGSE-NOE, Doble campo pulsado gradiente spin

NOESY es la determinación de las orientaciones relativas de los átomos en una molécula, por ejemplo, una proteína u otra molécula biológica grande, produciendo una estructura tridimensional. HOESY es la correlación cruzada NOESY entre átomos de diferentes elementos. ROESY implica el bloqueo de giro de la magnetización para evitar que llegue a cero, aplicado a moléculas para las que NOESY regular no es aplicable. TRNOE mide el NOE entre dos moléculas diferentes que interactúan en la misma solución, como en un ligando que se une a una proteína. En un experimento DPFGSE-NOE, un experimento transitorio que permite la supresión de señales fuertes y, por lo tanto, la detección de NOE muy pequeños.

Ejemplos del efecto Overhauser nuclear

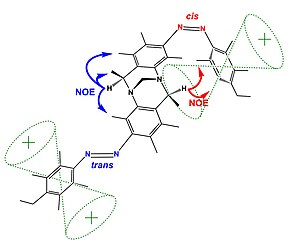
La figura (arriba) muestra cómo la espectroscopia de efecto Overhauser nuclear puede dilucidar la estructura de un compuesto conmutable. En este ejemplo, el protón designado como {H} muestra dos conjuntos diferentes de NOEs según el estado de isomerización (cis o trans) de los grupos azo intercambiables. En el estado trans, el protón {H} está lejos del grupo fenilo y muestra NOEs de color azul; mientras que el estado cis mantiene el protón {H} en la vecindad del grupo fenilo, lo que da como resultado la aparición de nuevos NOE (mostrado en rojo).

Otro ejemplo (abajo) donde la aplicación donde el NOE es útil para asignar resonancias y determinar la configuración son los polisacáridos. Por ejemplo, los glucanos complejos poseen una multitud de señales superpuestas, especialmente en un espectro de protones. Por lo tanto, es ventajoso utilizar experimentos de RMN 2D que incluyan NOESY para la asignación de señales. Ver, por ejemplo, NOE de carbohidratos.

Más resultados...