Efecto Joule-Thomson

En termodinámica, el efecto Joule-Thomson (también conocido como efecto Joule-Kelvin o efecto Kelvin-Joule) describe el cambio de temperatura de un gas real o líquido (a diferencia de un gas ideal) cuando se fuerza a través de una válvula o tapón poroso mientras se mantiene aislado para que no se intercambie calor con el medio ambiente. Este procedimiento se denomina proceso de regulación o proceso Joule-Thomson. A temperatura ambiente, todos los gases, excepto el hidrógeno, el helio y el neón, se enfrían al expandirse mediante el proceso Joule-Thomson cuando se estrangula a través de un orificio; estos tres gases experimentan el mismo efecto pero solo a temperaturas más bajas. La mayoría de los líquidos, como los aceites hidráulicos, se calentarán mediante el proceso de estrangulamiento de Joule-Thomson.

El proceso de estrangulamiento de enfriamiento de gas se explota comúnmente en procesos de refrigeración como licuefactores en procesos industriales de separación de aire. En hidráulica, el efecto de calentamiento del estrangulamiento de Joule-Thomson se puede utilizar para encontrar válvulas con fugas internas, ya que producirán calor que se puede detectar con un termopar o una cámara termográfica. El estrangulamiento es un proceso fundamentalmente irreversible. El estrangulamiento debido a la resistencia al flujo en las líneas de suministro, intercambiadores de calor, regeneradores y otros componentes de las máquinas (térmicas) es una fuente de pérdidas que limita su rendimiento.

Historia

El efecto lleva el nombre de James Prescott Joule y William Thomson, primer barón de Kelvin, quienes lo descubrieron en 1852. Siguió un trabajo anterior de Joule sobre la expansión Joule, en el que un gas se expande libremente en el vacío y la temperatura es sin cambios, si el gas es ideal.

Descripción

La expansión adiabática (sin intercambio de calor) de un gas puede llevarse a cabo de varias formas. El cambio de temperatura que experimenta el gas durante la expansión depende no sólo de la presión inicial y final, sino también de la forma en que se lleva a cabo la expansión.

• Si el proceso de expansión es reversible, lo que significa que el gas está en equilibrio termodinámico en todo momento, se llama un istrópico expansión. En este escenario, el gas hace un trabajo positivo durante la expansión, y su temperatura disminuye.
• En una expansión libre, por otro lado, el gas no funciona y no absorbe calor, por lo que se conserva la energía interna. Ampliada de esta manera, la temperatura de un gas ideal permanecería constante, pero la temperatura de un gas real disminuye, excepto a muy alta temperatura.
• El método de expansión discutido en este artículo, en el que un gas o líquido a presión P₁ flujos hacia una región de menor presión P₂ sin cambios significativos en la energía cinética, se llama la expansión Joule-Thomson. La expansión es inherentemente irreversible. Durante esta expansión, el enthalpy permanece sin cambios (ver la prueba abajo). A diferencia de una expansión libre, se realiza el trabajo, causando un cambio en la energía interna. Si la energía interna aumenta o disminuye se determina por si el trabajo se realiza en o por el fluido; que es determinado por los estados iniciales y finales de la expansión y las propiedades del líquido.

Signo del coeficiente Joule-Thomson, μ μ JT{displaystyle mu _{mathrm {JT}} para N₂. Dentro de la región atada por la línea roja, una expansión Joule-Thomson produce enfriamiento (0}" xmlns="http://www.w3.org/1998/Math/MathML">μ μ JT■0{displaystyle mu _{mathrm {JT}} {}}}}}}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f6284cf3c777d8105764d34e142b3d5ef1c402e6" style="vertical-align: -0.838ex; width:7.926ex; height:2.676ex;"/>); fuera de esa región, la expansión produce calefacción. La curva de convivencia gas-líquida se muestra por la línea azul, terminando en el punto crítico (el círculo azul sólido). Las líneas desgarradas demarcan la región donde N₂ es un fluido supercritico (donde las propiedades transiciones suavemente entre líquido y gas).

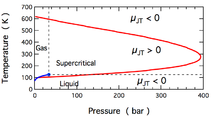
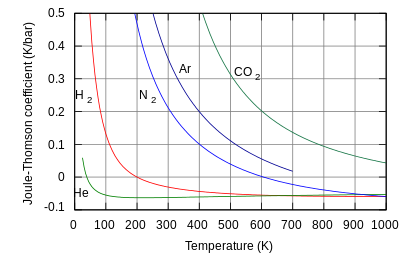
El cambio de temperatura producido durante una expansión Joule-Thomson está cuantificado por el coeficiente Joule-Thomson, μ μ JT{displaystyle mu _{mathrm {JT}}. Este coeficiente puede ser positivo (correspondiente al enfriamiento) o negativo (calor); las regiones donde cada uno ocurre para nitrógeno molecular, N₂, se muestran en la figura. Note que la mayoría de las condiciones en la figura corresponden a N₂ ser un fluido supercritico, donde tiene algunas propiedades de un gas y algunos de un líquido, pero no se puede describir realmente como ser tampoco. El coeficiente es negativo tanto a temperaturas muy altas como muy bajas; a muy alta presión es negativo a todas las temperaturas. Temperatura máxima de inversión (621 K para N₂) ocurre cuando se acerca la presión cero. Para N₂ gas a bajas presiones, μ μ JT{displaystyle mu _{mathrm {JT}} es negativo a altas temperaturas y positivo a bajas temperaturas. A temperaturas inferiores a la curva de convivencia gas-liquid, N₂ se condensa para formar un líquido y el coeficiente vuelve negativo. Así pues, para N₂ gas debajo de 621 K, una expansión Joule-Thomson se puede utilizar para enfriar el gas hasta líquido N₂ formas.

Mecanismo físico

Hay dos factores que pueden cambiar la temperatura de un fluido durante una expansión adiabática: un cambio en la energía interna o la conversión entre energía interna potencial y cinética. La temperatura es la medida de la energía cinética térmica (energía asociada con el movimiento molecular); por lo que un cambio en la temperatura indica un cambio en la energía cinética térmica. La energía interna es la suma de la energía cinética térmica y la energía potencial térmica. Así, incluso si la energía interna no cambia, la temperatura puede cambiar debido a la conversión entre energía cinética y potencial; esto es lo que sucede en una expansión libre y normalmente produce una disminución de la temperatura a medida que el fluido se expande. Si se realiza trabajo sobre o por el fluido a medida que se expande, entonces la energía interna total cambia. Esto es lo que sucede en una expansión de Joule-Thomson y puede producir un calentamiento o enfriamiento mayor que el observado en una expansión libre.

En una expansión Joule-Thomson el enthalpy sigue siendo constante. El enthalpy, H{displaystyle H., se define como

H=U+PV{displaystyle H=U+PV}

Donde U{displaystyle U} es energía interna, P{displaystyle P} es presión, y V{displaystyle V} es volumen. Bajo las condiciones de una expansión Joule-Thomson, el cambio en PV{displaystyle PV! representa el trabajo realizado por el fluido (ver la prueba siguiente). Si PV{displaystyle PV! aumentos, con H{displaystyle H. constante, entonces U{displaystyle U} debe disminuir como resultado del fluido que hace trabajo en su entorno. Esto produce una disminución de la temperatura y resulta en un coeficiente positivo Joule-Thomson. Por el contrario, una disminución PV{displaystyle PV! significa que el trabajo se realiza en el fluido y aumenta la energía interna. Si el aumento de la energía cinética supera el aumento de la energía potencial, habrá un aumento de la temperatura del fluido y el coeficiente Joule-Thomson será negativo.

Para un gas ideal, PV{displaystyle PV! no cambia durante una expansión Joule-Thomson. Como resultado, no hay cambios en la energía interna, ya que no hay cambios en la energía potencial térmica, no puede haber cambio en la energía cinética térmica y, por lo tanto, no hay cambio en la temperatura. En gases reales, PV{displaystyle PV! cambia.

La relación del valor PV{displaystyle PV! a que se espera para un gas ideal a la misma temperatura se llama el factor de compresión, Z{displaystyle Z}. Para un gas, esto es normalmente menos que la unidad a baja temperatura y mayor que la unidad a alta temperatura (ver la discusión en el factor de compresión). A baja presión, el valor de Z{displaystyle Z} Siempre se mueve hacia la unidad a medida que se expande el gas. Así a baja temperatura, Z{displaystyle Z} y PV{displaystyle PV! aumentará a medida que el gas se expanda, dando lugar a un coeficiente positivo Joule-Thomson. A alta temperatura, Z{displaystyle Z} y PV{displaystyle PV! disminuir a medida que el gas se expanda; si la disminución es lo suficientemente grande, el coeficiente Joule-Thomson será negativo.

Para líquidos, y para fluidos supercríticos bajo alta presión, PV{displaystyle PV! aumenta a medida que aumenta la presión. Esto se debe a que las moléculas son forzadas juntas, por lo que el volumen apenas puede disminuir debido a una presión superior. En tales condiciones, el coeficiente Joule-Thomson es negativo, como se ve en la figura anterior.

El mecanismo físico asociado con el efecto Joule-Thomson está estrechamente relacionado con el de una onda de choque, aunque una onda de choque difiere en que el cambio en la energía cinética global del flujo de gas no es despreciable.

El coeficiente Joule-Thomson (Kelvin)

Fig. 1 – Coeficientes Joule–Thomson para varios gases a presión atmosférica

La tasa de cambio de temperatura T{displaystyle T} con respecto a la presión P{displaystyle P} en un proceso Joule-Thomson (es decir, en constante enthalpy H{displaystyle H.) es el Coeficiente Joule-Thomson (Kelvin) μ μ JT{displaystyle mu _{mathrm {JT}}. Este coeficiente se puede expresar en términos del volumen del gas V{displaystyle V}, su capacidad de calor a presión constante Cp{displaystyle C_{mathrm {}}}, y su coeficiente de expansión térmica α α {displaystyle alpha } como:

μ μ JT=()∂ ∂ T∂ ∂ P)H=VCp()α α T− − 1){displaystyle mu _{mathrm {JT}=left({partial) T over partial P}right)_{H}={frac {V}{C_{mathrm {}} {alpha T-1),}

Vea el § Derivación del coeficiente Joule-Thomson a continuación para la prueba de esta relación. El valor de μ μ JT{displaystyle mu _{mathrm {JT}} se expresa normalmente en °C/bar (unidades SI: K/Pa) y depende del tipo de gas y de la temperatura y presión del gas antes de la expansión. Su dependencia de presión es generalmente sólo un poco por ciento para las presiones hasta 100 bar.

Todos los gases reales tienen punto de inversión en que el valor μ μ JT{displaystyle mu _{mathrm {JT}} cambios de señal. La temperatura de este punto, la Temperatura de inversión Joule-Thomson, depende de la presión del gas antes de la expansión.

En una expansión de gas la presión disminuye, por lo que el signo de ∂ ∂ P{displaystyle partial P} es negativo por definición. Con eso en mente, la siguiente tabla explica cuando el efecto Joule-Thomson enfría o calienta un gas real:

Si la temperatura del gas es	entonces μ μ JT{displaystyle mu _{text{JT}} es	desde entonces ∂ ∂ P{displaystyle partial P} es	por lo tanto ∂ ∂ T{displaystyle partial T} Debe ser	así que el gas
debajo de la temperatura de inversión	positivo	siempre negativo	negativo	cools
sobre la temperatura de inversión	negativo		positivo	calor

El helio y el hidrógeno son dos gases cuyas temperaturas de inversión Joule-Thomson a una presión de una atmósfera son muy bajas (por ejemplo, alrededor de 45 K, −228 °C para el helio). Por lo tanto, el helio y el hidrógeno se calientan cuando se expanden a entalpía constante a temperatura ambiente típica. Por otro lado, el nitrógeno y el oxígeno, los dos gases más abundantes en el aire, tienen temperaturas de inversión de 621 K (348 °C) y 764 K (491 °C) respectivamente: estos gases pueden ser enfriados desde la temperatura ambiente por el Joule– efecto Thomson.

Para un gas ideal, μ μ JT{displaystyle mu _{text{JT}} es siempre igual a cero: gases ideales no calientes ni frescos al ser expandidos a la enthalpy constante.

Aplicaciones

En la práctica, el efecto Joule-Thomson se logra al permitir que el gas se expanda a través de un dispositivo regulador (generalmente una válvula) que debe estar muy bien aislado para evitar cualquier transferencia de calor hacia o desde el gas. No se extrae trabajo externo del gas durante la expansión (el gas no debe expandirse a través de una turbina, por ejemplo).

El enfriamiento producido en la expansión Joule-Thomson la convierte en una herramienta valiosa en refrigeración. El efecto se aplica en la técnica de Linde como un proceso estándar en la industria petroquímica, donde el efecto de enfriamiento se usa para licuar gases y también en muchas aplicaciones criogénicas (por ejemplo, para la producción de oxígeno líquido, nitrógeno y argón). Un gas debe estar por debajo de su temperatura de inversión para ser licuado por el ciclo de Linde. Por esta razón, los licuefactores de ciclo Linde simples, a partir de la temperatura ambiente, no se pueden utilizar para licuar helio, hidrógeno o neón. Sin embargo, el efecto Joule-Thomson se puede utilizar para licuar incluso el helio, siempre que el helio gaseoso se enfríe primero por debajo de su temperatura de inversión de 40 K.

Prueba de que la entalpía específica permanece constante

En termodinámica, los llamados "específicos" Las cantidades son cantidades por unidad de masa (kg) y se indican con caracteres en minúsculas. Entonces, h, u y v son la entalpía específica, la energía interna específica y el volumen específico (volumen por unidad de masa o densidad recíproca), respectivamente. En un proceso Joule-Thomson, la entalpía específica h permanece constante. Para probar esto, el primer paso es calcular el trabajo neto realizado cuando una masa m del gas se mueve a través del tapón. Esta cantidad de gas tiene un volumen de V₁ = m v₁ en la región a la presión P₁ (región 1) y un volumen V₂ = m v₂ cuando en la región a presión P₂ (región 2). Luego, en la región 1, el "trabajo de flujo" hecho sobre la cantidad de gas por el resto del gas es: W₁ = m P ₁v₁. En la región 2, el trabajo realizado por la cantidad de gas sobre el resto del gas es: W₂ = m P₂v₂. Entonces, el trabajo total realizado sobre la masa m de gas es

W=mP1v1− − mP2v2.{displaystyle W=mP_{1}v_{1}-mP_{2}v_{2}

El cambio en la energía interna menos el trabajo total realizado sobre la cantidad de gas es, según la primera ley de la termodinámica, el calor total suministrado a la cantidad de gas.

U− − W=Q{displaystyle U-W=Q}

En el proceso Joule-Thomson, el gas está aislado, por lo que no se absorbe calor. Esto significa que

()mu2− − mu1)− − ()mP1v1− − mP2v2)=0mu1+mP1v1=mu2+mP2v2u1+P1v1=u2+P2v2{displaystyle {begin{aligned}(mu_{2}-mu_{1} ¿Qué?

donde u₁ y u₂ indican las energías internas específicas del gas en las regiones 1 y 2, respectivamente. Usando la definición de la entalpía específica h = u + Pv, la ecuación anterior implica que

h1=h2{displaystyle h_{1}=h_{2}

donde h₁ y h₂ indican las entalpías específicas de la cantidad de gas en las regiones 1 y 2, respectivamente.

Estrangulamiento en el diagrama T-s

Fig. 2 – T-s diagrama de nitrógeno. La cúpula roja representa la región de dos fases con el lado de baja entropía (el líquido saturado) y el lado de alta entropía (el gas saturado). Las curvas negras dan T-s relación a lo largo de isobars. Las presiones se indican en la barra. Las curvas azules son isenthalps (curvas de enthalpy específico constante). Los enthalpies específicos se indican en kJ/kg. Los puntos específicos a, b, etc., se tratan en el texto principal.

Una forma muy conveniente de obtener una comprensión cuantitativa del proceso de estrangulamiento es mediante el uso de diagramas como los diagramas h-T, h- diagramas P, y otros. Comúnmente se utilizan los llamados diagramas T-s. La figura 2 muestra el diagrama T-s del nitrógeno como ejemplo. Varios puntos se indican a continuación:

Como se muestra antes, la limitación mantiene h constante. P.ej. el estrangulamiento de 200 bar y 300 K (punto a en la fig. 2) sigue la isentálpica (línea de entalpía específica constante) de 430 kJ/kg. A 1 bar da como resultado el punto b que tiene una temperatura de 270 K. Por lo tanto, la estrangulación de 200 bar a 1 bar proporciona un enfriamiento desde la temperatura ambiente hasta por debajo del punto de congelación del agua. El estrangulamiento de 200 bar y una temperatura inicial de 133 K (punto c en la fig. 2) a 1 bar da como resultado el punto d, que se encuentra en la región de dos fases del nitrógeno en una temperatura de 77,2 K. Dado que la entalpía es un parámetro extenso, la entalpía en d (h_d) es igual a la entalpía en e (h_e) multiplicado por la fracción de masa del líquido en d (x_d) más la entalpía en f (h_f ) multiplicado por la fracción de masa del gas en d (1 − x_d). Entonces

hd=xdhe+()1− − xd)hf.{displaystyle ¿Qué?

Con números: 150 = x_d 28 + (1 − x_d) 230 entonces x_d es aproximadamente 0,40. Esto significa que la fracción de masa del líquido en la mezcla de líquido y gas que sale de la válvula de estrangulación es del 40 %.

Derivación del coeficiente Joule-Thomson

Es difícil pensar físicamente en lo que el coeficiente Joule-Thomson, μ μ JT{displaystyle mu _{mathrm {JT}}, representa. Además, determinaciones modernas de μ μ JT{displaystyle mu _{mathrm {JT}} no use el método original utilizado por Joule y Thomson, sino que mida una cantidad diferente y estrechamente relacionada. Por lo tanto, es útil derivar relaciones entre μ μ JT{displaystyle mu _{mathrm {JT}} y otras cantidades más convenientemente medidas, como se describe a continuación.

El primer paso para obtener estos resultados es notar que el coeficiente de Joule-Thomson involucra las tres variables T, P y H. Se obtiene inmediatamente un resultado útil aplicando la regla cíclica; en términos de estas tres variables esa regla puede escribirse

()∂ ∂ T∂ ∂ P)H()∂ ∂ H∂ ∂ T)P()∂ ∂ P∂ ∂ H)T=− − 1.{displaystyle left({frac {partial T}{partial P}right)_{H}left({frac {partial H}{partial T}right)_{P}left({frac {partial P}{right)_{T}=-1.}

Cada uno de los tres derivados parciales en esta expresión tiene un significado específico. El primero μ μ JT{displaystyle mu _{mathrm {JT}}, el segundo es la capacidad de calor de presión constante, Cp{displaystyle C_{mathrm {}}}, definida por

Cp=()∂ ∂ H∂ ∂ T)P{displaystyle C_{mathrm {}=left({frac {partial H}{partial T}right)_{P}}}

y el tercero es el inverso del coeficiente isotérmico Joule–Thomson, μ μ T{displaystyle mu _{mathrm {T}}, definida por

μ μ T=()∂ ∂ H∂ ∂ P)T{displaystyle mu _{mathrm {T}=left({frac {partial H}{partial P}right)_{T}}.

Esta última cantidad es más fácil de medir que μ μ JT{displaystyle mu _{mathrm {JT}}. Así, la expresión de la regla cíclica se convierte en

μ μ JT=− − μ μ TCp.{displaystyle mu _{mathrm}=-{frac {mu} - ¿Qué?

Esta ecuación se puede utilizar para obtener los coeficientes de Joule-Thomson a partir del coeficiente de Joule-Thomson isotérmico que se mide más fácilmente. Se utiliza a continuación para obtener una expresión matemática del coeficiente de Joule-Thomson en términos de las propiedades volumétricas de un fluido.

Para continuar, el punto de partida es la ecuación fundamental de la termodinámica en términos de entalpía; esto es

dH=TdS+VdP.{displaystyle mathrm {d} H=Tmathrm {d} S+Vmathrm {d} P.}

Ahora "dividiendo entre" por dP, manteniendo la temperatura constante, produce

()∂ ∂ H∂ ∂ P)T=T()∂ ∂ S∂ ∂ P)T+V{displaystyle left({frac {partial H}{partial P}right)_{T}=Tleft({frac {partial S}{partial P}right)_{T}+V}

El derivado parcial a la izquierda es el coeficiente isotérmico Joule–Thomson, μ μ T{displaystyle mu _{mathrm {T}}, y el de la derecha se puede expresar en términos del coeficiente de expansión térmica a través de una relación Maxwell. La relación apropiada es

()∂ ∂ S∂ ∂ P)T=− − ()∂ ∂ V∂ ∂ T)P=− − Vα α {displaystyle left({frac {partial S}{partial P}right)_{T}=-left({frac {partial V}{partial T}right)_{P}=-Valpha ,}

donde α es el coeficiente cúbico de expansión térmica. Reemplazando estas dos derivadas parciales se obtiene

μ μ T=− − TVα α +V.{displaystyle mu _{mathrm {T}=-TValpha +V.}

Esta expresión ahora puede sustituir μ μ T{displaystyle mu _{mathrm {T}} en la ecuación anterior para μ μ JT{displaystyle mu _{mathrm {JT}} para obtener:

μ μ JT↑ ↑ ()∂ ∂ T∂ ∂ P)H=VCp()α α T− − 1).{displaystyle mu _{mathrm {JT}equiv left({frac {partial T}{partial P}right)_{H}={frac {V}{C_{mathrm {}} {alpha T-1).,}

Esto proporciona una expresión para el coeficiente Joule-Thomson en términos de la capacidad de calor de propiedades comúnmente disponibles, volumen molar y coeficiente de expansión térmica. Muestra que la temperatura de inversión Joule-Thomson, a la que μ μ JT{displaystyle mu _{mathrm {JT}} es cero, ocurre cuando el coeficiente de expansión térmica es igual al inverso de la temperatura. Puesto que esto es cierto a todas las temperaturas para gases ideales (ver expansión en gases), el coeficiente Joule-Thomson de un gas ideal es cero a todas las temperaturas.

Segunda ley de Joule

Es fácil verificar que para un gas ideal definido por postulados microscópicos adecuados que αT = 1, entonces el cambio de temperatura de tal gas ideal en una expansión de Joule-Thomson es cero. Para tal gas ideal, este resultado teórico implica que:

La energía interna de una masa fija de gas ideal depende sólo de su temperatura (no de presión o volumen).

Esta regla fue encontrada originalmente por Joule experimentalmente para gases reales y se conoce como segunda ley de Joule. Experimentos más refinados encontraron desviaciones importantes de él.