Efecto Hall Cuántico

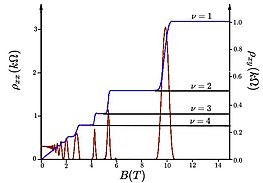
El efecto Hall cuántico (o efecto Hall cuántico entero) es una versión cuantizada del efecto Hall que se observa en sistemas electrónicos bidimensionales sometidos a bajas temperaturas y fuertes campos magnéticos, en los que la resistencia de Hall R_xy exhibe pasos que toman los valores cuantificados

${displaystyle R_{xy}={frac {fnK}} {fnK}}= {fnMicroc} {h}{e^{2}nu}}}$

donde V_Hall es el voltaje Hall, I< /i>_channel es el canal actual, e es la carga elemental y h es la constante de Planck. El divisor ν puede tomar cualquier número entero (ν = 1, 2, 3,...) o fraccionario (ν = 1< span class="sr-only">/3, 2/5, 3/7, 2/3, 3/ 5, 1< span class="sr-only">/5, 2/9, < span class="num">3/13, 5/2 , 12/5,...) valores. Aquí, ν es aproximadamente pero no exactamente igual al factor de relleno de los niveles de Landau. El efecto Hall cuántico se conoce como efecto Hall cuántico entero o fraccional dependiendo de si ν es un número entero o una fracción, respectivamente.

La característica sorprendente del efecto Hall cuántico entero es la persistencia de la cuantificación (es decir, la meseta de Hall) a medida que varía la densidad electrónica. Dado que la densidad electrónica permanece constante cuando el nivel de Fermi está en un espacio espectral limpio, esta situación corresponde a una en la que el nivel de Fermi es una energía con una densidad finita de estados, aunque estos estados están localizados (ver localización de Anderson).

El efecto Hall cuántico fraccional es más complicado y todavía se considera un problema de investigación abierto. Su existencia se basa fundamentalmente en las interacciones electrón-electrón. En 1988, se propuso que existía un efecto Hall cuántico sin niveles de Landau. Este efecto Hall cuántico se denomina efecto Hall anómalo cuántico (QAH). También hay un nuevo concepto del efecto Hall de espín cuántico, que es un análogo del efecto Hall cuántico, en el que fluyen corrientes de espín en lugar de corrientes de carga.

Aplicaciones

La cuantificación de la conducta del Salón (${displaystyle G_{xy}=1/R_{xy}$) tiene la propiedad importante de ser extremadamente precisa. Se han encontrado mediciones reales de la conducta de la Sala que son múltiplos enteros o fraccionados de e²/h a casi una parte en mil millones. Ha permitido la definición de un nuevo estándar práctico para la resistencia eléctrica, basado en el cuántico de resistencia dado por la constante von Klitzing R_K. Esto se llama por Klaus von Klitzing, el descubridor de la cuantificación exacta. El efecto cuántico Hall también proporciona una determinación independiente extremadamente precisa de la constante de la estructura fina, una cantidad de importancia fundamental en la electrodinámica cuántica.

En 1990, un valor fijo convencional R_{K- 90} = 25812.807 Ω se definió para su uso en calibraciones de resistencia en todo el mundo. El 16 de noviembre de 2018, la 26.ª reunión de la Conferencia General de Pesos y Medidas decidió fijar valores exactos de h (la constante de Planck) y e (el cargo elemental), reemplazando el valor de 1990 con un valor permanente exacto R< sub>K = h/e² = 25812.80745... Ω.

Estado de la investigación

La sala cuántica entera se considera parte de la cuantificación exacta. La cuantización exacta en toda su generalidad no se comprende por completo, pero se ha explicado como una manifestación muy sutil de la combinación del principio de invariancia de calibre junto con otra simetría (ver Anomalías). En cambio, la sala cuántica entera se considera un problema de investigación resuelto y se comprende en el ámbito de la fórmula TKNN y los lagrangianos de Chern-Simons.

El efecto Hall cuántico fraccional todavía se considera un problema de investigación abierto. El efecto Hall cuántico fraccionario también puede entenderse como un efecto Hall cuántico entero, aunque no de electrones sino de compuestos de flujo de carga conocidos como fermiones compuestos. También existen otros modelos para explicar el Efecto Hall Cuántico Fraccionario. Actualmente se considera un problema de investigación abierto porque no existe una lista única, confirmada y consensuada de números cuánticos fraccionarios, ni un modelo único consensuado para explicarlos todos, aunque existen tales afirmaciones en el ámbito de los fermiones compuestos y Chern-Simons no abelianos. Lagrangianos.

Historia

El MOSFET (transistor de efecto de campo semiconductor de óxido de metal), inventado por Mohamed Atalla y Dawon Kahng en Bell Labs en 1959, permitió a los físicos estudiar el comportamiento de los electrones en un gas bidimensional casi ideal. En un MOSFET, los electrones de conducción viajan en una fina capa superficial y una "puerta" El voltaje controla el número de portadores de carga en esta capa. Esto permite a los investigadores explorar los efectos cuánticos al operar MOSFET de alta pureza a temperaturas de helio líquido.

La cuantización entera de la conductancia de Hall fue predicha originalmente por los investigadores Tsuneya Ando, Yukio Matsumoto y Yasutada Uemura de la Universidad de Tokio en 1975, sobre la base de un cálculo aproximado que ellos mismos no creían que fuera cierto. En 1978, los investigadores de la Universidad de Gakushuin, Jun-ichi Wakabayashi y Shinji Kawaji, observaron posteriormente el efecto en experimentos realizados en la capa de inversión de los MOSFET.

En 1980, Klaus von Klitzing, trabajando en el laboratorio de alto campo magnético en Grenoble con muestras MOSFET basadas en silicio desarrolladas por Michael Pepper y Gerhard Dorda, hizo el inesperado descubrimiento de que la resistencia de Hall era exactamente cuantificado. Por este hallazgo, von Klitzing recibió el Premio Nobel de Física de 1985. Posteriormente, Robert Laughlin propuso un vínculo entre la cuantificación exacta y la invariancia del calibre, quien conectó la conductividad cuantificada con el transporte de carga cuantificado en una bomba de carga Thouless. La mayoría de los experimentos de Hall cuánticos enteros ahora se realizan en heteroestructuras de arseniuro de galio, aunque se pueden usar muchos otros materiales semiconductores. En 2007, se informó el efecto Hall cuántico entero en el grafeno a temperaturas tan altas como la temperatura ambiente, y en el óxido de magnesio y zinc ZnO–Mg_xZn_{1− x}O.

Efecto Hall cuántico entero

Niveles Landau

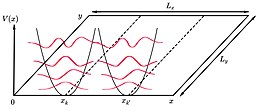
En dos dimensiones, cuando los electrones clásicos se someten a un campo magnético, siguen órbitas circulares de ciclotrón. Cuando el sistema se trata mecánicamente cuánticamente, estas órbitas se cuantifican. Para determinar los valores de los niveles de energía se debe resolver la ecuación de Schrödinger.

Dado que el sistema está sujeto a un campo magnético, tiene que ser introducido como un potencial vectorial electromagnético en la ecuación Schrödinger. El sistema considerado es un gas de electrones que es libre de moverse en las direcciones x y y, pero se limita firmemente en la dirección z. Luego, un campo magnético se aplica en la dirección z y según el calibre Landau el potencial vectorial electromagnético es ${displaystyle mathbf {A} =(0,Bx,0)}$ y el potencial de escalar ${displaystyle phi =0}$. Así la ecuación Schrödinger para una partícula de carga ${displaystyle q}$ y masa efectiva ${displaystyle m^{*}$ en este sistema:

${displaystyle left{frac {1}{2m^{*}}left[mathbf {p} -qmathbf {A}right]^{2}+V(z)right}psi (x,y,z)=varepsilon psi (x,y,z)}$

Donde ${displaystyle mathbf {p}$ es el impulso canónico, que es reemplazado por el operador ${displaystyle - ihbar nabla }$ y ${displaystyle varepsilon }$ es la energía total.

Para resolver esta ecuación es posible separarla en dos ecuaciones ya que el campo magnético sólo afecta el movimiento a lo largo de los ejes x y y. La energía total se convierte entonces, la suma de dos contribuciones ${displaystyle varepsilon =varepsilon _{z}+varepsilon ¿Qué?$. Las ecuaciones correspondientes en el eje z son:

${displaystyle left[-{frac {hbar ^{2}{2m^{*}}{partial ^{2} over partial z^{2}+V(z)right]u(z)=varepsilon _{z}u(z)}$

Para simplificar las cosas, la solución ${displaystyle V(z)}$ es considerado como un pozo infinito. Así las soluciones para la dirección z son las energías ${textstyle varepsilon ¿Qué? {n_{z} {2}pi} ¿Qué?$, ${displaystyle No.$ y las funciones de onda son sinusoidales. Para el ${displaystyle x}$ y ${displaystyle y}$ direcciones, la solución de la ecuación Schrödinger se puede elegir para ser el producto de una onda de avión en ${displaystyle y}$-dirección con alguna función desconocida ${displaystyle x}$, es decir, ${displaystyle psi _{xy}=u(x)e^{ik_{y}y}$. Esto es porque el potencial vectorial no depende de ${displaystyle y}$ y el operador de impulso ${displaystyle {hat {}_{y}}$ por lo tanto, se comunica con el Hamiltonian. Al sustituir este Ansatz en la ecuación Schrödinger uno consigue la ecuación de oscilador armónico de una dimensión centrada en ${textstyle ################################################################################################################################################################################################################################################################ {hbar k_{y}{eB}} {f}} {f}}} {f}}}}} {f}}}}}}}} {f}}}}}}} {f}}}}}}} {f}}}}}}}}} {f}} {f}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$.

${displaystyle left[-{frac {hbar ^{2}{2m^{*}}{partial ^{2} over partial x^{2}}+{2}m^{*}omega _{rm {c}}{2}(x-l_{B}^{2}k_{y})^{2}right]u(x)=varepsilon _{xy}u(x)}$

Donde ${textstyle omega _{rm {c}={frac} {EB} {m^{*}}}$ se define como la frecuencia del ciclotrón y ${textstyle ¿Qué?$ la longitud magnética. Las energías son:

${displaystyle varepsilon ¿Por qué? _{n_{x}=hbar omega _{rm {c}left(n_{x}+{frac {1}{2}right)}$, ${displaystyle No.$

Y las funciones de onda para el movimiento en el ${displaystyle xy}$ plano son dados por el producto de una ola de avión en ${displaystyle y}$ y polinomios hermitas atenuados por la función gaussiana en ${displaystyle x}$, que son las funciones de onda de un oscilador armónico.

De la expresión para los niveles de Landau uno nota que la energía depende sólo de ${displaystyle n_{x}$, no en ${displaystyle K_{y}$. Estados con los mismos ${displaystyle n_{x}$ pero diferente ${displaystyle K_{y}$ son degenerados.

Densidad de estados

En el campo cero, la densidad de estados por unidad de superficie para el gas de electrones bidimensional teniendo en cuenta la degeneración debida al espín es independiente de la energía

${displaystyle n_{rm}={frac {m^{*}{pihbar ^{2}}}}}} {f}}}} {f}}}} {f}}}}}} {f}}}}}}}} {f}}}}}$.

A medida que se activa el campo, la densidad de los estados colapsa de la constante a un peine Dirac, una serie de Dirac ${displaystyle delta }$ funciones correspondientes a los niveles de Landau separados ${displaystyle Delta varepsilon _{xy}=hbar omega _{rm {c}}$. A temperatura finita, sin embargo, los niveles de Landau adquieren un ancho ${textstyle Gamma ={hbar }{tau _{i}}}$ estar ${displaystyle tau _{i}$ el tiempo entre los eventos de dispersión. Comúnmente se supone que la forma precisa de los niveles de Landau es un perfil gaisiano o lorentziano.

Otra característica es que las funciones de onda forman tiras paralelas en la ${displaystyle y}$ - la dirección espaciada igual a lo largo de la ${displaystyle x}$-eje, según las líneas ${displaystyle mathbf {A}$. Ya que no hay nada especial en ninguna dirección ${displaystyle xy}$-plane si el potencial vectorial fue elegido diferentemente uno debe encontrar simetría circular.

Dada una muestra de dimensiones ${displaystyle L_{x}times L... {y}$ y aplicación de las condiciones de los límites periódicos ${displaystyle y}$-dirección ${fnMicroc {2fnMicroc} } {L_{y}}j}$ estar ${displaystyle j}$ un entero, uno consigue que cada potencial parabólico se coloca en un valor ${displaystyle ¿Qué?$.

Potencias parabólicas a lo largo de los ${displaystyle x}$-Eje centrado en ${displaystyle x_{k}$ con las funciones de la primera ola correspondientes a un pozo infinito ${displaystyle z}$ dirección. En el ${displaystyle y}$- dirección hay olas de avión.

El número de estados para cada nivel de Landau y ${displaystyle k}$ se puede calcular a partir de la relación entre el flujo magnético total que pasa a través de la muestra y el flujo magnético correspondiente a un estado.

${displaystyle No. ¿Qué? Delta {fnK}= {fnK} {fnK} {fnK}}= {fnK}} {fn} {fnK}} {fnK}}}} {fnK}}} {fnK}}} {fnK}}} {f}fnKf}f}}}}f}}}}f}}}}}}}}\\\fnfnfnfnfnfnfnfnKf}fnKf}fnKfnfnKf}fnf}f}fnKfnKfnKfnKfnfnKfnf}fnfnfnKf}fnKfnKfnKfnKfnfnKf}fnKf}f}fn {B}{2}} {begin{lcr} reducidal_{B} lentamente} {f}} {frac}} {begin{array}} {begin{lcr}} {f} {f} {fnK}}}} {begin{b}}}} {begin{b}}}{b}}}}}}{begin {begin {b}}}}}}{begin {begin{begin {begin {begin {b}}}}}}}}}}{begin {begin {begin}}}}}}}}}}}}}}{begin {begin {begin {begin {begin{begin {b}}}}}}}}}}}}}}}}}}}}}}}}}}{begin{begin{begin {begin {begin {b}}} {AeB}{2pihbar {c}{begin{array} {cr}{rm {c} {c} {c} {c} {c}}{begin {array} {c}}}{begin{begin {array}{c}{c}}{c}}}}{begin{begin {begin{}}}}{begin {begin{c}}}}}}}}{c}}}}{begin {begin {begin {c} {c}{c}}{c}}}}}{c}}}}}{c}}}}}}}{c} {c}}{c}}}}}{c}{c}{c}}}}}}}}{c}}}}}}}}}{c}{c}}}}{c}}}}{c}}}}}}}}}} {m^{*}omega _{rm}A}{2pihbar}$

Por lo tanto, la densidad de estados por unidad de superficie es

${displaystyle ################################################################################################################################################################################################################################################################ {c}}{2pihbar}}} {c}} {c}} {c}} {c} {c}}} {c}}}} {c}}} {c}} {c}}} {c}} {c}} {c}} {c}}}}} {c}}}}}}}}}{2c}}}}}}}}}}}}}}}}{2c}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}} {c}}}}}}}}}}}}}}}}}{2c}}}}}}}}}}}}}}} {c}}}}} {cc}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$.

Observe la dependencia de la densidad de estados con el campo magnético. Cuanto más grande es el campo magnético, más estados hay en cada nivel de Landau. Como consecuencia, hay más confinamiento en el sistema ya que se ocupan menos niveles de energía.

Reescribir la última expresión como ${textstyle No. {hbar omega _{rm {c}}{2}{frac} {f}} {fnK}}} {f}}} {f}} {f}}} {fn}}} {f}}} {fn}}} {fn}}} {f}}}} {f}}}}} {f}} {f}}}}}} {f} {f}}}} {f}}} {f}}}} {f}}} {f}}}} {f}}} {f} {f} {f}}}}} {f}f}}}}}}}}}}}}}} {f}} {f}f}}}}}}} {f} {f} {f} {f} {f} {f} {f}}}}}}}f}f}}}f}}}}}f}}}}}}}}}} {m^{*}{pihbar ^{2}}} {f} {f}} {f}} {f}}} {f}}}}} {f}}}}}} {f}}}}}}} {f}}}}} {f}}}}} {f}}}}}}}}}}}}}}} {\\f}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ está claro que cada nivel de Landau contiene tantos estados como en un 2DEG en un ${displaystyle Delta varepsilon =hbar omega _{rm {c}}}$.

Dado que los electrones son fermions, para cada estado disponible en los niveles de Landau corresponde a dos electrones, un electrón con cada valor para la columna ${textstyle s=pm {frac {1}{2}}}$. Sin embargo, si se aplica un gran campo magnético, las energías se dividen en dos niveles debido al momento magnético asociado con la alineación de la columna con el campo magnético. La diferencia en las energías es ${textstyle Delta E=pm {frac}gmu _{rm {B}B}$ estar ${displaystyle g}$ un factor que depende del material (${displaystyle g=2}$ para electrones libres) y ${displaystyle mu _{rm {B}}$ el imán Bohr. La señal ${displaystyle +}$ se toma cuando el giro es paralelo al campo y ${displaystyle -}$ cuando es antiparalelo. Este hecho llamado división de giro implica que la densidad de estados para cada nivel se reduce en una mitad. Note que ${displaystyle Delta E}$ es proporcional al campo magnético así que, cuanto más grande es el campo magnético, más relevante es la división.

Densidad de estados en un campo magnético, descuidando la división del giro. a) Los estados de cada rango ${displaystyle hbar omega _{rm {c}}$ son apretados en un ${displaystyle delta }$- Funcionamiento del nivel de Landau.(b) Los niveles de Landau tienen una anchura no cero ${displaystyle "Gamma"$ en una imagen más realista y solapamiento si ${displaystyle hbar omega _{rm [c] Gamma.$. c) Los niveles se hacen distintos cuando ${displaystyle hbar omega _{rm {c}] Gamma.$.

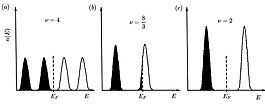
Para obtener el número de niveles ocupados de Landau, se define el denominado factor de llenado ${displaystyle nu }$ como la relación entre la densidad de estados en un 2DEG y la densidad de estados en los niveles de Landau.

${displaystyle nu ={frac {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn}}} {fn_}}}} {fn}}} {fn}}} {fn}}} {fn_}} {fn_}}}}}} {fn_}}}}}} {f}}}}}}}}}}}}}}} {f}} {n_\\f}} {f}}}}} {f}} {f}}}}}}}}}}}}}}}}}}}}} {f}}}} {f} {f}}} {f}}} {f}}}}}}}}}}}}}}}}} {f} {f}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {hn_{rm {2D}} {eB}}} {}}} {cH}}}} {cH}}}} {cH}}}}}}}} {cH}}}}}}}}} {cH}}}} {}}}} {}}}}} {}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

En general el factor de llenado ${displaystyle nu }$ no es un entero. Resulta que es un número entero cuando hay un número exacto de niveles de Landau llenos. En cambio, se convierte en un no-integer cuando el nivel superior no está completamente ocupado. Desde ${displaystyle No.$, al aumentar el campo magnético, los niveles de Landau se mueven en energía y el número de estados en cada nivel crece, por lo que menos electrones ocupan el nivel superior hasta que se vacía. Si el campo magnético sigue aumentando, eventualmente, todos los electrones estarán en el nivel más bajo de Landau (${displaystyle nu$) y esto se llama el límite cuántico magnético.

Ocupación de los niveles de Landau en un campo magnético descuidando la división del giro, mostrando cómo el nivel de Fermi se mueve para mantener una densidad constante de electrones. Los campos están en la relación ${displaystyle 2:3:4}$ y dar ${displaystyle nu =4,{frac {8}{3}}$ y ${displaystyle 2}$.

Resistividad longitudinal

Es posible relacionar el factor de llenado con la resistividad y, por lo tanto, con la conductividad del sistema. Cuando ${displaystyle nu }$ es un entero, la energía Fermi se encuentra entre los niveles de Landau donde no hay estados disponibles para los transportistas, por lo que la conductividad se convierte en cero (se considera que el campo magnético es lo suficientemente grande para que no haya superposición entre los niveles de Landau, de lo contrario habría pocos electrones y la conductividad sería aproximadamente ${displaystyle 0}$). En consecuencia, la resistividad se convierte en cero también (en campos magnéticos muy altos se demuestra que la conductividad longitudinal y la resistividad son proporcionales).

Con la conductividad ${displaystyle sigma =rho ^{-1}$ uno encuentra

${displaystyle sigma = {1}{det rho {begin{pmatrix}rho - ¿Qué? ¿Por qué? - ¿Qué? ¿Qué?$

Si la resistividad longitudinal es cero y transversal es finita, entonces ${displaystyle det rho neq 0}$. Así, la conductividad longitudinal y la resistividad se convierten en cero.

En lugar de eso, cuando ${displaystyle nu }$ es un medio entero, la energía Fermi se encuentra en el pico de la distribución de densidad de algún nivel de Landau. Esto significa que la conductividad tendrá un máximo.

Esta distribución de mínimos y máximos corresponde a ¨oscilaciones cuánticas¨ denominadas oscilaciones de Shubnikov-de Haas que se vuelven más relevantes a medida que aumenta el campo magnético. Obviamente, la altura de los picos es mayor a medida que aumenta el campo magnético, ya que la densidad de estados aumenta con el campo, por lo que hay más portadores que contribuyen a la resistividad. Es interesante notar que si el campo magnético es muy pequeño, la resistividad longitudinal es constante, lo que significa que se alcanza el resultado clásico.

Resistencia longitudinal y transversal (Hall) ${displaystyle rho _{xx}}$ y ${displaystyle rho _{xy}}$, de un gas de electrones bidimensional como función de campo magnético. Ambos ejes verticales fueron divididos por la unidad cuántica de conducta ${displaystyle e^{2}/h}$ (Las unidades son engañosas). El factor de llenado ${displaystyle nu }$ se muestra en la última 4 meseta.

Resistividad transversal

De la relación clásica de la resistividad transversal ${textstyle rho {fnMicrosoft Sans Serif} {2D}}}}$ y sustitución $################################################################################################################################################################################################################################################################ {2D}=nu {f} {f}} {f}}} {f}}} {fn}} {f}}} {f}}}}}}} {f}}}} {f}}}}}}}} {\\\\\\\\\\\fn}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$ se encuentra la cuantificación de la resistencia y conductividad transversales:

${displaystyle rho _{xy}={frac {h}{nu e^{2}\fn} Rightarrow sigma =nu {frac {}} {}} {}} {}} {}}} {}}}}} {}}} {}}}} {}}}} {}}}}}}} {}}}}}} {}} {}}}}}}}}} {}}}}} {}}} {}}}}}}}} {}}}}}} {}}}}}}}} {}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Uno concluye entonces, que la resistividad transversal es un múltiplo del inverso del llamado cuántico conductance ${displaystyle e^{2}/h}$. Sin embargo, en los experimentos se observa una meseta entre los niveles de Landau, lo que indica que hay de hecho portadores de carga presentes. Estos transportistas se localizan, por ejemplo, en impurezas del material donde están atrapados en órbitas para que no puedan contribuir a la conductividad. Por eso la resistividad sigue siendo constante entre los niveles de Landau. Una vez más, si el campo magnético disminuye, se obtiene el resultado clásico en el que la resistividad es proporcional al campo magnético.

Efecto Hall cuántico fotónico

El efecto Hall cuántico, además de observarse en sistemas electrónicos bidimensionales, puede observarse en fotones. Los fotones no poseen carga eléctrica inherente, pero a través de la manipulación de resonadores ópticos discretos y fases de acoplamiento o fases in situ, se puede crear un campo magnético artificial. Este proceso se puede expresar a través de una metáfora de fotones que rebotan entre múltiples espejos. Al disparar la luz a través de múltiples espejos, los fotones se enrutan y ganan una fase adicional proporcional a su momento angular. Esto crea un efecto como si estuvieran en un campo magnético.

Matemáticas

Mariposa de Hofstadter

Los números enteros que aparecen en el efecto Hall son ejemplos de números cuánticos topológicos. Son conocidos en matemáticas como los primeros números de Chern y están estrechamente relacionados con la fase de Berry. Un modelo sorprendente de mucho interés en este contexto es el modelo de Azbel-Harper-Hofstadter cuyo diagrama de fase cuántica es la mariposa de Hofstadter que se muestra en la figura. El eje vertical es la fuerza del campo magnético y el eje horizontal es el potencial químico, que fija la densidad electrónica. Los colores representan las conductancias Hall enteras. Los colores cálidos representan números enteros positivos y los colores fríos números enteros negativos. Tenga en cuenta, sin embargo, que la densidad de estados en estas regiones de conductancia Hall cuantificada es cero; por lo tanto, no pueden producir las mesetas observadas en los experimentos. El diagrama de fase es fractal y tiene estructura en todas las escalas. En la figura hay una autosemejanza evidente. En presencia de desorden, que es la fuente de las mesetas vistas en los experimentos, este diagrama es muy diferente y la estructura fractal se elimina en su mayor parte.

Con respecto a los mecanismos físicos, las impurezas y/o estados particulares (p. ej., corrientes de borde) son importantes tanto para el 'entero' y 'fraccional' efectos Además, la interacción de Coulomb también es esencial en el efecto Hall cuántico fraccional. La fuerte similitud observada entre los efectos Hall cuánticos enteros y fraccionarios se explica por la tendencia de los electrones a formar estados ligados con un número par de cuantos de flujo magnético, llamados fermiones compuestos.

La interpretación atómica de Bohr de la constante de von Klitzing

El valor de la constante de Von Klitzing puede obtenerse ya en el nivel de un átomo único dentro del modelo Bohr mientras lo mira como un efecto de Hall de un solo electrón. Mientras que durante el movimiento de ciclotron en una órbita circular la fuerza centrífuga está equilibrada por la fuerza Lorentz responsable del voltaje inducido transversal y el efecto Hall, se puede ver la diferencia potencial de Coulomb en el átomo Bohr como el voltaje de átomo único inducido y el movimiento de electrones periódicos en un círculo como corriente Hall. Definir la corriente de un solo átomo Hall como una tasa de un solo electron carga ${displaystyle e}$ está haciendo revoluciones Kepler con frecuencia angular ${displaystyle omega }$

${displaystyle I={frac {omega e}{2pi}}}$

y el voltaje de Hall inducido como diferencia entre el potencial de Coulomb del núcleo de hidrógeno en el punto orbital del electrón y en el infinito:

${displaystyle U=V_{text{C}(infty)-V_{text{C}(r)=0-V_{text{C}(r)={frac {e}{4piepsilon ¿Qué?$

Se obtiene la cuantificación de la resistencia de Hall de la órbita de Bohr definida en pasos de la constante de von Klitzing como

${displaystyle ¿Qué? {h}{e^{2}}}$

que para el átomo de Bohr es lineal pero no inverso en el entero n.

Análogos relativistas

Los ejemplos relativistas del efecto Hall cuántico entero y el efecto Hall de espín cuántico surgen en el contexto de la teoría de calibre de red.