Ecuaciones de Lotka-Volterra

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Equations modelling predator-prey cycles

Las ecuaciones de Lotka-Volterra, también conocidas como modelo depredador-presa de Lotka-Volterra, son un par de ecuaciones diferenciales no lineales de primer orden, utilizadas con frecuencia para describir la dinámica de los sistemas biológicos en los que interactúan dos especies, una como depredador y la otra como presa. Las poblaciones cambian a través del tiempo según el par de ecuaciones:

{displaystyle {begin{aligned}{frac {dx}{dt}}&=alpha x-beta xy,\{frac {dy}{dt}}&=delta xy-gamma y,end{aligned}}}

dónde

la variable $x$ es la densidad poblacional de la presa (por ejemplo, el número de conejos por kilómetro cuadrado);
la variable $Sí.$ es la densidad de población de algunos depredadores (por ejemplo, el número de zorros por kilómetro cuadrado);
${tfrac {dy}{dt}}$ y ${tfrac {dx}{dt}}$ representan las tasas de crecimiento instantáneas de las dos poblaciones;
$t$ representa tiempo;
Los parámetros de la presa, $α$ y $β$ , describir, respectivamente, la tasa máxima de crecimiento per cápita de presas y el efecto de la presencia de depredadores en la tasa de crecimiento de presas.
Los parámetros del depredador, $γ$ , $δ$ , respectivamente describir la tasa de mortalidad per cápita del depredador, y el efecto de la presencia de presa en la tasa de crecimiento del depredador.
Todos los parámetros son positivos y reales.

La solución de las ecuaciones diferenciales es determinista y continua. Esto, a su vez, implica que las generaciones tanto del depredador como de la presa se superponen continuamente.

El sistema de ecuaciones de Lotka-Volterra es un ejemplo de un modelo de Kolmogorov, que es un marco más general que puede modelar la dinámica de los sistemas ecológicos con interacciones depredador-presa, competencia, enfermedades y mutualismo.

Interpretación biológica y supuestos del modelo

Se supone que la presa tiene un suministro ilimitado de alimentos y se reproduce exponencialmente, a menos que esté sujeta a depredación; este crecimiento exponencial está representado en la ecuación anterior por el término $αx$ . Se supone que la tasa de depredación de la presa es proporcional a la tasa a la que se encuentran los depredadores y la presa; esto está representado arriba por $βxy$ . Si $x$ o $y$ es cero, entonces no puede haber depredación. Con estos dos términos, la ecuación de presa anterior se puede interpretar de la siguiente manera: la tasa de cambio de la población de la presa está dada por su propia tasa de crecimiento menos la tasa a la que es depredada.

El término $δxy$ representa el crecimiento de la población de depredadores. (Obsérvese la similitud con la tasa de depredación; sin embargo, se utiliza una constante diferente, ya que la tasa a la que crece la población de depredadores no es necesariamente igual a la tasa a la que consume la presa). El término $γy$ representa la tasa de pérdida de los depredadores debido a muerte natural o emigración; conduce a una decadencia exponencial en ausencia de presas. Por tanto, la ecuación expresa que la tasa de cambio de la población del depredador depende de la tasa a la que consume a sus presas, menos su tasa de mortalidad intrínseca.

El modelo depredador-presa de Lotka-Volterra hace una serie de suposiciones sobre el medio ambiente y la biología de las poblaciones de depredadores y presas:

La población presa encuentra alimentos amplios en todo momento.
El suministro de alimentos de la población depredador depende totalmente del tamaño de la población de presas.
La tasa de cambio de población es proporcional a su tamaño.
Durante el proceso, el medio ambiente no cambia a favor de una especie, y la adaptación genética es inconsecuente.
Los depredadores tienen apetito ilimitado.
Ambas poblaciones pueden ser descritas por una sola variable. Esto equivale a suponer que las poblaciones no tienen una distribución espacial o de edad que contribuye a la dinámica.

Relevancia biológica del modelo

Es probable que ninguna de las suposiciones anteriores se cumpla para las poblaciones naturales. Sin embargo, el modelo Lotka-Volterra muestra dos propiedades importantes de las poblaciones de depredadores y presas y estas propiedades a menudo se extienden a variantes del modelo en las que estos supuestos son relajados:

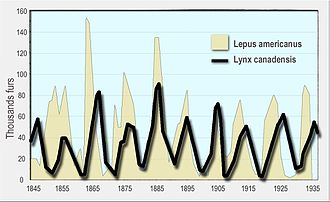
En primer lugar, la dinámica de las poblaciones de depredadores y presas tiende a oscilar. Se han observado números fluctuantes de depredadores y presas en poblaciones naturales, como los datos de linces y liebres con raquetas de nieve de la Compañía de la Bahía de Hudson y las poblaciones de alces y lobos en el Parque Nacional Isle Royale.

En segundo lugar, el equilibrio de población de este modelo tiene la propiedad de la densidad de equilibrio de presas (procedida por ${displaystyle x=gamma /delta }$ ) depende de los parámetros del depredador, y de la densidad de equilibrio del depredador (dadada por ${displaystyle y=alpha /beta }$ ) en los parámetros de la presa. Esto tiene como consecuencia que un aumento en, por ejemplo, la tasa de crecimiento de presas, $alpha$ , conduce a un aumento en la densidad de equilibrio depredador, pero no la densidad de equiilbrium de presa. Mejorar el medio ambiente para la presa beneficia al depredador, no a la presa (esto está relacionado con la paradoja de los pesticidas y con la paradoja del enriquecimiento). Una demostración de este fenómeno es proporcionada por el aumento del porcentaje de peces depredadores capturados había aumentado durante los años de la Primera Guerra Mundial (1914-18), cuando la tasa de crecimiento de presas se incrementó debido a una reducción del esfuerzo pesquero.

Otro ejemplo lo proporciona la fertilización experimental con hierro del océano. En varios experimentos se disolvieron grandes cantidades de sales de hierro en el océano. La expectativa era que el hierro, que es un nutriente limitante para el fitoplancton, impulsaría el crecimiento del fitoplancton y es decir, secuestraría dióxido de carbono de la atmósfera. La adición de hierro normalmente conduce a una breve floración del fioplancton, que es rápidamente consumido por otros organismos (como peces pequeños o zooplancton) y limita el efecto del enriquecimiento principalmente a una mayor densidad de depredadores, lo que a su vez limita el secuestro de carbono. Esto es lo que predicen las densidades de población en equilibrio del modelo depredador-presa de Lotka-Volterra, y es una característica que se traslada a modelos más elaborados en los que se relajan los supuestos restrictivos del modelo simple.

Aplicaciones a la Economía y al Marketing

El modelo Lotka Volterra tiene aplicaciones adicionales en áreas como la economía y el marketing. Puede usarse para describir la dinámica en un mercado con varios competidores, plataformas y productos complementarios, una economía colaborativa y más. Hay situaciones en las que uno de los competidores expulsa a los demás del mercado y otras situaciones en las que el mercado alcanza un equilibrio en el que cada empresa estabiliza su participación de mercado. También es posible describir situaciones en las que hay cambios cíclicos en la industria o situaciones caóticas sin equilibrio y los cambios son frecuentes e impredecibles.

Historia

El modelo depredador-presa de Lotka-Volterra fue propuesto inicialmente por Alfred J. Lotka en la teoría de reacciones químicas autocatalíticas en 1910. Esta era efectivamente la ecuación logística, originalmente derivada por Pierre François Verhulst. En 1920, Lotka amplió el modelo, a través de Andrey Kolmogorov, a los "sistemas orgánicos" usando una especie de planta y una especie de animal herbívoro como ejemplo y en 1925 usó las ecuaciones para analizar las interacciones depredador-presa en su libro sobre biomatemática. El mismo conjunto de ecuaciones fue publicado en 1926 por Vito Volterra, un matemático y físico que se había interesado por la biología matemática. La investigación de Volterra se inspiró en sus interacciones con el biólogo marino Umberto D'Ancona, quien en ese momento cortejaba a su hija y más tarde se convertiría en su yerno. D'Ancona estudió las capturas de peces en el mar Adriático y observó que el porcentaje de peces depredadores capturados había aumentado durante los años de la Primera Guerra Mundial (1914-18). Esto lo desconcertó, ya que el esfuerzo de pesca se había reducido mucho durante los años de la guerra y, como los peces de presa eran la captura preferida, uno intuitivamente esperaría que esto aumentara el porcentaje de peces de presa. Volterra desarrolló su modelo para explicar la observación de D'Ancona y lo hizo independientemente de Alfred Lotka. En su publicación, dio crédito al trabajo anterior de Lotka, después de lo cual el modelo pasó a ser conocido como el "modelo Lotka-Volterra".

El modelo se amplió posteriormente para incluir el crecimiento de las presas dependiente de la densidad y una respuesta funcional de la forma desarrollada por C. S. Holling; un modelo que se conoce como modelo Rosenzweig-MacArthur. Tanto el modelo de Lotka-Volterra como el de Rosenzweig-MacArthur se han utilizado para explicar la dinámica de las poblaciones naturales de depredadores y presas.

A finales de la década de 1980, surgió una alternativa al modelo depredador-presa de Lotka-Volterra (y sus generalizaciones dependientes de presas comunes), el modelo dependiente de la proporción o modelo Arditi-Ginzburg. La validez de los modelos dependientes de la presa o de la proporción ha sido muy debatida.

Las ecuaciones de Lotka-Volterra tienen una larga historia de uso en la teoría económica; su solicitud inicial se atribuye comúnmente a Richard Goodwin en 1965 o 1967.

Soluciones de las ecuaciones

Las ecuaciones tienen soluciones periódicas. Estas soluciones no tienen una expresión simple en términos de las funciones trigonométricas habituales, aunque son bastante manejables.

Si ninguno de los parámetros no negativos $α$ , $β$ , $γ$ , $δ$ desaparece, se pueden absorber tres en la normalización de variables para dejar solo un parámetro: dado que la primera ecuación es homogénea en $x$ , y el segundo en $y$ , los parámetros β/ α y δ/γ son absorbibles en las normalizaciones de $y$ y $x$ respectivamente, y $γ$ en la normalización de $t$ , de modo que solo $α / γ$ sigue siendo arbitrario. Es el único parámetro que afecta la naturaleza de las soluciones.

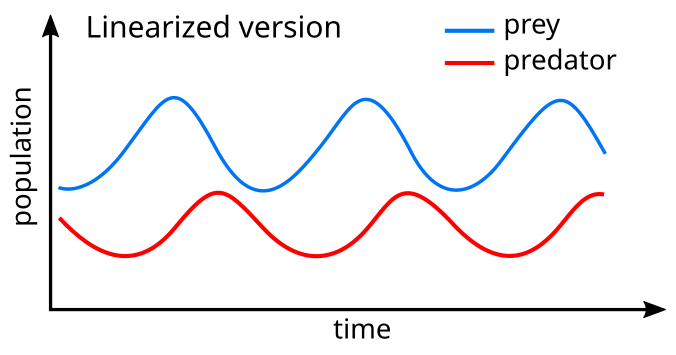
Una linealización de las ecuaciones produce una solución similar al movimiento armónico simple con la población de depredadores siguiendo a la de presas 90° en el ciclo.

Un ejemplo sencillo

Supongamos que hay dos especies de animales, un conejo (presa) y un zorro (depredador). Si las densidades iniciales son 10 conejos y 10 zorros por kilómetro cuadrado, se puede trazar la progresión de las dos especies a lo largo del tiempo; dados los parámetros que las tasas de crecimiento y muerte de los conejos son 1,1 y 0,4 mientras que las de los zorros son 0,1 y 0,4 respectivamente. La elección del intervalo de tiempo es arbitraria.

También se pueden trazar soluciones paramétricamente como órbitas en el espacio de fase, sin representar el tiempo, pero con un eje representando el número de presas y el otro eje representando las densidades de depredadores para todos los tiempos.

Esto corresponde a eliminar el tiempo de las dos ecuaciones diferenciales anteriores para producir una única ecuación diferencial.

{displaystyle {frac {dy}{dx}}=-{frac {y}{x}}{frac {delta x-gamma }{beta y-alpha }}}

relacionando las variables x y y. Las soluciones de esta ecuación son curvas cerradas. Es susceptible de separación de variables: integrando

{displaystyle {frac {beta y-alpha }{y}},dy+{frac {delta x-gamma }{x}},dx=0}

produce la relación implícita

{displaystyle V=delta x-gamma ln(x)+beta y-alpha ln(y),}

donde V es una cantidad constante que depende de las condiciones iniciales y se conserva en cada curva.

Un comentario aparte: estos gráficos ilustran una limitación potencial grave en la aplicación como modelo biológico: para esta elección específica de parámetros, en cada ciclo, la población de conejos se reduce a números extremadamente bajos, pero se recupera (mientras que la población de zorros permanece). considerable en la densidad más baja de conejos). Sin embargo, en situaciones de la vida real, las fluctuaciones aleatorias de los números discretos de individuos podrían causar que los conejos se extingan y, en consecuencia, también los zorros. Este problema de modelado se ha denominado "problema del atto-zorro", siendo un atto-zorro un 10⁻¹⁸ teórico de un zorro. Una densidad de 10⁻¹⁸ zorros por kilómetro cuadrado equivale a un promedio de aproximadamente 5×10⁻¹⁰ zorros en la superficie de la tierra, lo que en términos prácticos significa que los zorros están extintos.

Estructura hamiltoniana del sistema

Desde la cantidad ${displaystyle V(x,y)}$ se conserva con el tiempo, juega papel de una función Hamiltoniana del sistema. Para ver esto podemos definir el corchete Poisson como sigue ${displaystyle {f,g}=-xyleft({frac {partial f}{partial x}}{frac {partial g}{partial y}}-{frac {partial f}{partial y}}{frac {partial g}{partial x}}right)}$ . Entonces las ecuaciones de Hamilton leen

{displaystyle {begin{cases}{dot {x}}={x,V}=alpha x-beta xy,\{dot {y}}={y,V}=delta xy-gamma y.end{cases}}}

x

y

{displaystyle {x,y}=-xyneq 1}

{displaystyle p=ln(x)}

{displaystyle q=ln(y)}

{displaystyle H(q,p)=V(x(q,p),y(q,p))=delta e^{p}-gamma p+beta e^{q}-alpha q}

{displaystyle {begin{cases}{dot {q}}={frac {partial H}{partial p}}=delta e^{p}-gamma\{dot {p}}=-{frac {partial H}{partial q}}=alpha -beta e^{q}.end{cases}}}

Gráfico de espacio de fases de otro ejemplo

Un ejemplo menos extremo cubre:

$α = 2/3$ , $β = 4/3, γ = 1 = δ . Supongamos x, y cuantificar miles cada uno. Los círculos representan las condiciones iniciales de presa y depredador de x = y = 0,9 a 1,8, en pasos de 0,1. El punto fijo está en (1, 1/2).$

Dinámica del sistema

En el sistema modelo, los depredadores prosperan cuando las presas son abundantes pero, en última instancia, superan su suministro de alimentos y disminuyen. A medida que la población de depredadores sea baja, la población de presas aumentará nuevamente. Estas dinámicas continúan en un ciclo poblacional de crecimiento y disminución.

Equilibrio poblacional

El equilibrio de la población ocurre en el modelo cuando ninguno de los niveles de población cambia, es decir, cuando ambas derivadas son iguales a 0:

{displaystyle x(alpha -beta y)=0,}

{displaystyle -y(gamma -delta x)=0.}

El sistema de ecuaciones anterior produce dos soluciones:

{displaystyle {y=0, x=0}}

{displaystyle left{y={frac {alpha }{beta }}, x={frac {gamma }{delta }}right}.}

Por lo tanto, hay dos equilibrios.

La primera solución representa efectivamente la extinción de ambas especies. Si ambas poblaciones están en 0, seguirán estando así indefinidamente. La segunda solución representa un punto fijo en el que ambas poblaciones mantienen sus números actuales distintos de cero y, en el modelo simplificado, lo hacen indefinidamente. Los niveles de población en los que se logra este equilibrio dependen de los valores elegidos de los parámetros α, β, γ y δ. .

Estabilidad de los puntos fijos

La estabilidad del punto fijo en el origen se puede determinar realizando una linealización utilizando derivadas parciales.

La matriz jacobiana del modelo depredador-presa es

{displaystyle J(x,y)={begin{bmatrix}alpha -beta y&-beta x\delta y&delta x-gamma end{bmatrix}}.}

Primer punto fijo (extinción)

Did you mean:

When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes

{displaystyle J(0,0)={begin{bmatrix}alpha &0\0&-gamma end{bmatrix}}.}

Los valores propios de esta matriz son

{displaystyle lambda _{1}=alphaquad lambda _{2}=-gamma.}

En el modelo $α$ y $γ$ son siempre mayores que cero y, como tal, el signo de los valores propios anteriores siempre será diferente. Por tanto, el punto fijo en el origen es un punto de silla.

La inestabilidad de este punto fijo es importante. Si fuera estable, poblaciones distintas de cero podrían verse atraídas hacia él y, como tal, la dinámica del sistema podría conducir a la extinción de ambas especies en muchos casos de niveles poblacionales iniciales. Sin embargo, como el punto fijo en el origen es un punto de silla y, por tanto, inestable, se deduce que la extinción de ambas especies es difícil en el modelo. (De hecho, esto sólo podría ocurrir si la presa fuera completamente erradicada artificialmente, provocando que los depredadores murieran de hambre. Si los depredadores fueran erradicados, la población de presas crecería sin límites en este modelo simple.) Las poblaciones de presas y depredadores pueden acercarse infinitamente a cero y aun así recuperarse.

Segundo punto fijo (oscilaciones)

Evaluar J en el segundo punto fijo conduce a

{displaystyle Jleft({frac {gamma }{delta }},{frac {alpha }{beta }}right)={begin{bmatrix}0&-{frac {beta gamma }{delta }}\{frac {alpha delta }{beta }}&0end{bmatrix}}.}

Los valores propios de esta matriz son

{displaystyle lambda _{1}=i{sqrt {alpha gamma }},quad lambda _{2}=-i{sqrt {alpha gamma }}.}

Como los eigenvalues son puramente imaginarios y conjugados entre sí, este punto fijo debe ser un centro para órbitas cerradas en las proximidades locales o una espiral atractiva o repulsiva. En sistemas conservadores, debe haber órbitas cerradas en las proximidades locales de puntos fijos que existen en el minima y máxima de la cantidad conservada. La cantidad conservada se deriva de arriba para ser ${displaystyle V=delta x-gamma ln(x)+beta y-alpha ln(y)}$ en órbitas. Así las órbitas sobre el punto fijo están cerradas y elípticas, por lo que las soluciones son periódicas, oscilando en un pequeño elipse alrededor del punto fijo, con una frecuencia ${displaystyle omega ={sqrt {lambda _{1}lambda _{2}}}={sqrt {alpha gamma }}}$ y período ${displaystyle T=2{pi }/({sqrt {lambda _{1}lambda _{2}}})}$ .

Como se ilustra en las oscilaciones circulantes en la figura anterior, las curvas de nivel son órbitas cerradas que rodean el punto fijo: los niveles del depredador y poblaciones de presas ciclo y oscilan sin amortiguar alrededor del punto fijo con frecuencia ${displaystyle omega ={sqrt {alpha gamma }}}$ .

El valor de la constante del movimiento $V$ , o, equivalentemente, $K = exp(- V)$ , ${displaystyle K=y^{alpha }e^{-beta y}x^{gamma }e^{-delta x}}$ , se puede encontrar para las órbitas cerradas cerca del punto fijo.

Aumentar $K$ acerca una órbita cerrada al punto fijo. El valor más grande de la constante $K$ se obtiene resolviendo el problema de optimización.

0}.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Sí.α α e− − β β Sí.xγ γ e− − δ δ x=Sí.α α xγ γ eδ δ x+β β Sí.restablecimiento restablecimiento maxx,Sí.■0.{displaystyle y^{alpha }e^{-beta Y... #={frac {y^{alpha }x^{gamma {}{e^{delta x+beta y}}longrightarrow max _{x,y titulada0}0}.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4edfd6b470aa763a964c68de61ee3dee6856ec35" style="vertical-align: -2.338ex; width:33.567ex; height:5.843ex;"/>

{displaystyle left({frac {gamma }{delta }},{frac {alpha }{beta }}right)}

{displaystyle K^{*}=left({frac {alpha }{beta e}}right)^{alpha }left({frac {gamma }{delta e}}right)^{gamma },}

e

Más resultados...