Ecuaciones de Euler (dinámica de fluidos)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Conjunto de ecuaciones hiperbólicas cuasilineales que rigen el flujo adiabático e invisivo

En dinámica de fluidos, las ecuaciones de Euler son un conjunto de ecuaciones diferenciales parciales cuasilineales que gobiernan el flujo adiabático y no viscoso. Llevan el nombre de Leonhard Euler. En particular, corresponden a las ecuaciones de Navier-Stokes con viscosidad cero y conductividad térmica cero.

Las ecuaciones de Euler se pueden aplicar a flujos incompresibles o compresibles. Las ecuaciones incompresibles de Euler consisten en ecuaciones de Cauchy para la conservación de la masa y el equilibrio del momento, junto con la condición de incompresibilidad de que la velocidad del flujo es un campo solenoidal. Las ecuaciones de Euler compresibles consisten en ecuaciones para la conservación de masa, equilibrio de momento y equilibrio de energía, junto con una ecuación constitutiva adecuada para la densidad de energía específica del fluido. Históricamente, Euler sólo derivó las ecuaciones de conservación de masa y equilibrio de momento. Sin embargo, la literatura sobre dinámica de fluidos a menudo se refiere al conjunto completo de ecuaciones de Euler compresibles (incluida la ecuación de energía) como "las ecuaciones de Euler compresibles".

Los caracteres matemáticos de las ecuaciones de Euler incompresibles y comprimibles son bastante diferentes. Para una densidad de fluido constante, las ecuaciones incompresibles se pueden escribir como una ecuación de advección cuasilineal para la velocidad del fluido junto con una ecuación elíptica de Poisson para la presión. Por otro lado, las ecuaciones de Euler comprimibles forman un sistema hiperbólico cuasilineal de ecuaciones de conservación.

Las ecuaciones de Euler se pueden formular en una "forma convectiva" (también llamada "forma lagrangiana") o una "forma de conservación" (también llamada "forma euleriana"). La forma convectiva enfatiza los cambios de estado en un marco de referencia que se mueve con el fluido. La forma de conservación enfatiza la interpretación matemática de las ecuaciones como ecuaciones de conservación para un volumen de control fijo en el espacio (lo cual es útil desde un punto de vista numérico).

Historia

Las ecuaciones de Euler aparecieron por primera vez en forma publicada en el artículo de Euler "Principes généraux du mouvement des fluides", publicado en Mémoires de l'Académie des Sciences de Berlin en 1757 (aunque Euler había presentado previamente su trabajo a la Academia de Berlín en 1752). Las ecuaciones de Euler estuvieron entre las primeras ecuaciones diferenciales parciales que se escribieron, después de la ecuación de onda. En el trabajo original de Euler, el sistema de ecuaciones constaba de las ecuaciones de momento y continuidad y, por tanto, estaba subdeterminado excepto en el caso de un flujo incompresible. Pierre-Simon Laplace proporcionó una ecuación adicional, llamada condición adiabática en 1816.

Durante la segunda mitad del siglo XIX, se descubrió que la ecuación relacionada con el equilibrio de energía debe mantenerse en todo momento para flujos compresibles, y la condición adiabática es una consecuencia de las leyes fundamentales en el caso de flujos suaves. soluciones. Con el descubrimiento de la teoría especial de la relatividad, los conceptos de densidad de energía, densidad de momento y tensión se unificaron en el concepto de tensor tensión-energía, y la energía y el momento también se unificaron en un solo concepto, el vector energía-momento..

Ecuaciones de Euler incompresibles con densidad constante y uniforme

En forma convectiva (es decir, la forma con el operador convectivo hecho explícito en la ecuación de momento), las ecuaciones de Euler incompresibles en caso de densidad constante en el tiempo y uniforme en el espacio son:

Ecuaciones de Euler incompresibles con densidad constante y uniforme ()forma convectiva o lagrangia)

${displaystyle left{{begin{aligned}{Dmathbf {u} over Dt}&=-nabla w+mathbf {g} \nabla cdot mathbf {u} &=0end{aligned}}right.}$

donde:

$mathbf u$ es el vector de velocidad de flujo, con componentes en un N- espacio dimensional $u_{1},u_{2},dotsu_{N}$ ,
${displaystyle {frac {D{boldsymbol {Phi }}}{Dt}}={frac {partial {boldsymbol {Phi }}}{partial t}}+mathbf {v} cdot nabla {boldsymbol {Phi }}}$ , para una función genérica (o campo) ${displaystyle {boldsymbol {Phi }}}$ denota su derivado material en el tiempo con respecto al campo advectivo $mathbf {v}$ y
${displaystyle nabla w}$ es el gradiente de lo específico (con el sentido de por unidad de masa) trabajo termodinámico, el término fuente interna, y
${displaystyle nabla cdot mathbf {u} }$ es la divergencia de velocidad de flujo.
$mathbf {g}$ representa aceleraciónes corporales (por unidad de masa) actuando en el continuum, por ejemplo gravedad, aceleraciónes inerciales, aceleración del campo eléctrico, etc.

La primera ecuación es la ecuación del momento de Euler con densidad uniforme (para esta ecuación tampoco podría ser constante en el tiempo). Al expandir la derivada material, las ecuaciones quedan:

{displaystyle left{{begin{aligned}{partial mathbf {u} over partial t}+(mathbf {u} cdot nabla)mathbf {u} &=-nabla w+mathbf {g} \nabla cdot mathbf {u} &=0end{aligned}}right.}

De hecho para un flujo con densidad uniforme $rho _{0}$ la identidad siguiente:

nabla wequiv nabla left({frac {p}{rho _{0}}}right)={frac {1}{rho _{0}}}nabla p

Donde $p$ es la presión mecánica. La segunda ecuación es la limitación incompresible, afirmando que la velocidad de flujo es un campo solenoideal (el orden de las ecuaciones no es causal, pero subraya el hecho de que la limitación incompresible no es una forma degenerada de la ecuación de continuidad, sino más bien de la ecuación de energía, ya que se hará evidente en lo siguiente). Notablemente, la ecuación de continuidad sería necesaria también en este caso incompresible como una tercera ecuación adicional en caso de densidad variable en el tiempo o variando en el espacio. Por ejemplo, con uniforme de densidad pero variable en el tiempo, la ecuación de continuidad a añadir al conjunto anterior correspondería a:

{frac {partial rho }{partial t}}=0

Entonces, el caso de densidad constante y uniforme es el único que no requiere la ecuación de continuidad como ecuación adicional, independientemente de la presencia o ausencia de la restricción incompresible. De hecho, el caso de las ecuaciones de Euler incompresibles con densidad constante y uniforme que se analiza aquí es un modelo de juguete que presenta sólo dos ecuaciones simplificadas, por lo que es ideal para fines didácticos, incluso si tiene una relevancia física limitada.

Las ecuaciones anteriores representan, respectivamente, la conservación de la masa (1 ecuación escalar) y el impulso (1 ecuación vectorial que contiene $N$ componentes de escalar, donde $N$ es la dimensión física del espacio de interés). Velocidad de flujo y presión son los llamados variables físicas.

En un sistema de coordenadas dado por ${displaystyle left(x_{1},dotsx_{N}right)}$ la velocidad y los vectores de fuerza externa $mathbf u$ y ${displaystyle mathbf {g} }$ componentes ${displaystyle (u_{1},dotsu_{N})}$ y ${displaystyle left(g_{1},dotsg_{N}right)}$ , respectivamente. Entonces las ecuaciones se pueden expresar en notación de subscripto como:

Singularities

{displaystyle left{{begin{aligned}{partial u_{i} over partial t}+sum _{j=1}^{N}{partial left(u_{i}u_{j}+wdelta _{ij}right) over partial x_{j}}&=g_{i}\sum _{i=1}^{N}{partial u_{i} over partial x_{i}}&=0end{aligned}}right.}

Donde $i$ y $j$ subscriptos etiquetan el N- componentes espaciales dimensionales, y $delta _{ij}$ es el Kroenecker delta. El uso de la notación de Einstein (donde la suma está implícita por índices repetidos en lugar de notación de sigma) también es frecuente.

Propiedades

Aunque Euler presentó por primera vez estas ecuaciones en 1755, muchas preguntas o conceptos fundamentales sobre ellas siguen sin respuesta.

En tres dimensiones espaciales, en ciertos escenarios simplificados, las ecuaciones de Euler producen singularidades.

Las soluciones suaves de las ecuaciones libres (en el sentido de sin término fuente: g=0) satisfacen la conservación de la energía cinética específica:

{displaystyle {partial over partial t}left({frac {1}{2}}u^{2}right)+nabla cdot left(u^{2}mathbf {u} +wmathbf {u} right)=0}

En el caso unidimensional sin el término fuente (tanto gradiente de presión como fuerza externa), la ecuación del momento se convierte en la ecuación invisible de Burgers:

{partial u over partial t}+u{partial u over partial x}=0

Este modelo de ecuación ofrece muchos conocimientos sobre las ecuaciones de Euler.

Did you mean:

Nondimensionalization

Para hacer las ecuaciones indimensionales, una longitud característica $r_{0}$ , y una velocidad característica $u_{0}$ , debe ser definido. Estos deben ser elegidos de tal manera que las variables sin dimensión son todas de orden uno. Así, se obtienen las siguientes variables indimensionales:

{displaystyle {begin{aligned}u^{*}&equiv {frac {u}{u_{0}}},\[5pt]r^{*}&equiv {frac {r}{r_{0}}},\[5pt]t^{*}&equiv {frac {u_{0}}{r_{0}}}t,\[5pt]p^{*}&equiv {frac {w}{u_{0}^{2}}},\[5pt]nabla ^{*}&equiv r_{0}nabla end{aligned}}}

y del vector unitario de campo:

{hat {mathbf {g} }}equiv {frac {mathbf {g} }{g}},

Did you mean:

Substitution of these inverse relations in Euler equations, defining the Froude number, yields (omitting the * at apex):

Ecuaciones de Euler incompresibles con densidad constante y uniforme ()forma no dimensionada)

${displaystyle left{{begin{aligned}{Dmathbf {u} over Dt}&=-nabla w+{frac {1}{mathrm {Fr} }}{hat {mathbf {g} }}\nabla cdot mathbf {u} &=0end{aligned}}right.}$

Las ecuaciones de Euler en el límite de Froude (sin campo externo) se denominan ecuaciones libres y son conservadoras. Por tanto, el límite de los números de Froude altos (campo externo bajo) es notable y puede estudiarse con la teoría de la perturbación.

Formulario de conservación

La forma de conservación enfatiza las propiedades matemáticas de las ecuaciones de Euler y, especialmente, la forma contraída suele ser la más conveniente para simulaciones de dinámica de fluidos computacional. Computacionalmente, existen algunas ventajas al utilizar variables conservadas. Esto da lugar a una gran clase de métodos numéricos. llamados métodos conservadores.

Las ecuaciones libres de Euler son conservadoras, en el sentido de que equivalen a una ecuación de conservación:

{displaystyle {frac {partial mathbf {y} }{partial t}}+nabla cdot mathbf {F} ={mathbf {0} },}

o simplemente en notación de Einstein:

{frac {partial y_{j}}{partial t}}+{frac {partial f_{ij}}{partial r_{i}}}=0_{i},

donde la cantidad de conservación $mathbf {y}$ en este caso es un vector, y $mathbf {F}$ es una matriz de flujo. Esto se puede probar simplemente.

Demostración de la forma de conservación

En primer lugar, las siguientes identidades sostienen:

{displaystyle nabla cdot (wmathbf {I})=mathbf {I} cdot nabla w+wnabla cdot mathbf {I} =nabla w}

{displaystyle mathbf {u} cdot nabla cdot mathbf {u} =nabla cdot (mathbf {u} otimes mathbf {u})}

Donde $otimes$ denota el producto exterior. Las mismas identidades expresadas en la notación de Einstein son:

{displaystyle partial _{i}left(wdelta _{ij}right)=delta _{ij}partial _{i}w+wpartial _{i}delta _{ij}=delta _{ij}partial _{i}w=partial _{j}w}

{displaystyle u_{j}partial _{i}u_{i}=partial _{i}left(u_{i}u_{j}right)}

donde soy la matriz de identidad con dimensión N y δ_ij su elemento general, el Kroenecker delta.

Gracias a estas identidades vectoriales, las ecuaciones incompresibles de Euler con densidad constante y uniforme y sin campo externo se pueden poner en el llamado conservación (o Eulerian) forma diferencial, con notación vectorial:

{displaystyle left{{begin{aligned}{partial mathbf {u} over partial t}+nabla cdot left(mathbf {u} otimes mathbf {u} +wmathbf {I} right)&=mathbf {0} \{partial 0 over partial t}+nabla cdot mathbf {u} &=0,end{aligned}}right.}

o con la notación de Einstein:

{displaystyle left{{begin{aligned}partial _{t}u_{j}+partial _{i}left(u_{i}u_{j}+wdelta _{ij}right)&=0\partial _{t}0+partial _{j}u_{j}&=0,end{aligned}}right.}

Entonces... incompresible Las ecuaciones de Euler con densidad uniforme tienen variables de conservación:

{displaystyle {mathbf {y} }={begin{pmatrix}mathbf {u} \0end{pmatrix}};qquad {mathbf {F} }={begin{pmatrix}mathbf {u} otimes mathbf {u} +wmathbf {I} \mathbf {u} end{pmatrix}}.}

Tenga en cuenta que en el segundo componente u es por sí mismo un vector, con la longitud N, por lo que y tiene la longitud N+1 y F tiene el tamaño N(N+1). En 3D por ejemplo y tiene longitud 4, tengo tamaño 3×3 y F tiene tamaño 4×3, así que las formas explícitas son:

{displaystyle {mathbf {y} }={begin{pmatrix}u_{1}\u_{2}\u_{3}\0end{pmatrix}};quad {mathbf {F} }={begin{pmatrix}u_{1}^{2}+w&u_{1}u_{2}&u_{1}u_{3}\u_{2}u_{1}&u_{2}^{2}+w&u_{2}u_{3}\u_{3}u_{1}&u_{3}u_{2}&u_{3}^{2}+w\u_{1}&u_{2}&u_{3}end{pmatrix}}.}

Por fin las ecuaciones de Euler se pueden reformular en la ecuación particular:

Ecuaciones de Euler incompresibles con densidad constante y uniforme ()conservación o forma euleria)

${displaystyle {frac {partial }{partial t}}{begin{pmatrix}mathbf {u} \0end{pmatrix}}+nabla cdot {begin{pmatrix}mathbf {u} otimes mathbf {u} +wmathbf {I} \mathbf {u} end{pmatrix}}={begin{pmatrix}mathbf {g} \0end{pmatrix}}}$

Dimensiones espaciales

Para ciertos problemas, especialmente cuando se utiliza para analizar el flujo compresible en un conducto o en caso de que el flujo sea cilíndrico o simétrico esférico, las ecuaciones Euler unidimensionales son una primera aproximación útil. Generalmente, las ecuaciones Euler se resuelven por el método de características de Riemann. Esto implica encontrar curvas en plano de variables independientes (es decir, $x$ y $t$ ) junto con las ecuaciones diferenciales parciales (PDEs) degeneran en ecuaciones diferenciales ordinarias (ODEs). Las soluciones numéricas de las ecuaciones Euler dependen en gran medida del método de características.

Ecuaciones de Euler incompresibles

En forma convectiva las ecuaciones de Euler incompresibles en caso de densidad variable en el espacio son:

Ecuaciones de Euler incompresibles ()forma convectiva o lagrangia)

${displaystyle left{{begin{aligned}{Drho over Dt}&=0\{Dmathbf {u} over Dt}&=-{frac {nabla p}{rho }}+mathbf {g} \nabla cdot mathbf {u} &=0end{aligned}}right.}$

donde las variables adicionales son:

$rho$ es la densidad de masa del fluido,
$p$ es la presión, $p=rho w$ .

La primera ecuación, que es la nueva, es la ecuación de continuidad incompresible. De hecho la ecuación general de continuidad sería:

{displaystyle {partial rho over partial t}+mathbf {u} cdot nabla rho +rho nabla cdot mathbf {u} =0}

pero aquí el último término es idénticamente cero para la restricción de incompresibilidad.

Formulario de conservación

Las ecuaciones de Euler incompresibles en el límite de Froude son equivalentes a una única ecuación de conservación con cantidad conservada y flujo asociado respectivamente:

{displaystyle {mathbf {y} }={begin{pmatrix}rho \rho mathbf {u} \0end{pmatrix}};qquad {mathbf {F} }={begin{pmatrix}rho mathbf {u} \rho mathbf {u} otimes mathbf {u} +pmathbf {I} \mathbf {u} end{pmatrix}}.}

Aquí. $mathbf {y}$ tiene longitud ${displaystyle N+2}$ y $mathbf {F}$ tiene tamaño ${displaystyle (N+2)N}$ . En general (no sólo en el límite Froude) Las ecuaciones de Euler son expresables como:

{displaystyle {frac {partial }{partial t}}{begin{pmatrix}rho \rho mathbf {u} \0end{pmatrix}}+nabla cdot {begin{pmatrix}rho mathbf {u} \rho mathbf {u} otimes mathbf {u} +pmathbf {I} \mathbf {u} end{pmatrix}}={begin{pmatrix}0\rho mathbf {g} \0end{pmatrix}}}

Variables de conservación

Las variables para las ecuaciones en forma de conservación aún no están optimizadas. De hecho podríamos definir:

{displaystyle {mathbf {y} }={begin{pmatrix}rho \mathbf {j} \0end{pmatrix}};qquad {mathbf {F} }={begin{pmatrix}mathbf {j} \{frac {1}{rho }},mathbf {j} otimes mathbf {j} +pmathbf {I} \{frac {mathbf {j} }{rho }}end{pmatrix}}.}

donde:

${displaystyle mathbf {j} =rho mathbf {u} }$ es la densidad de impulso, una variable de conservación.

Ecuaciones de Euler incompresibles ()conservación o forma euleria)

${displaystyle {frac {partial }{partial t}}{begin{pmatrix}rho \mathbf {j} \0end{pmatrix}}+nabla cdot {begin{pmatrix}mathbf {j} \{frac {1}{rho }},mathbf {j} otimes mathbf {j} +pmathbf {I} \{frac {mathbf {j} }{rho }}end{pmatrix}}={begin{pmatrix}0\mathbf {f} \0end{pmatrix}}}$

donde:

${displaystyle mathbf {f} =rho mathbf {g} }$ es la densidad de fuerza, una variable de conservación.

Ecuaciones de Euler

En forma convectiva diferencial, las ecuaciones de Euler comprimibles (y más generales) se pueden escribir brevemente con la notación derivada de material:

Ecuaciones de Euler ()forma convectiva)

${displaystyle left{{begin{aligned}{Drho over Dt}&=-rho nabla cdot mathbf {u} \[1.2ex]{frac {Dmathbf {u} }{Dt}}&=-{frac {nabla p}{rho }}+mathbf {g} \[1.2ex]{De over Dt}&=-{frac {p}{rho }}nabla cdot mathbf {u} end{aligned}}right.}$

donde las variables adicionales aquí son:

$e$ es la energía interna específica (energía interna por unidad).

Las ecuaciones anteriores representan así la conservación de masa, momento y energía: la ecuación de energía expresada en la energía interna variable permite comprender el vínculo con el caso incompresible, pero no en la forma más simple. La densidad de masa, la velocidad del flujo y la presión son las llamadas variables convectivas (o variables físicas, o variables lagrangianas), mientras que la densidad de masa, la densidad de momento y la densidad de energía total son las llamadas conservadas. variables (también llamadas variables eulerianas o matemáticas).

Si uno expande la derivada material, las ecuaciones anteriores son:

{displaystyle left{{begin{aligned}{partial rho over partial t}+mathbf {u} cdot nabla rho +rho nabla cdot mathbf {u} &=0\[1.2ex]{frac {partial mathbf {u} }{partial t}}+mathbf {u} cdot nabla mathbf {u} +{frac {nabla p}{rho }}&=mathbf {g} \[1.2ex]{partial e over partial t}+mathbf {u} cdot nabla e+{frac {p}{rho }}nabla cdot mathbf {u} &=0end{aligned}}right.}

Restricción incompresible (revisada)

Volviendo al caso incompresible, ahora resulta evidente que la restricción incompresible típica de los casos anteriores es en realidad una forma particular válida para flujos incompresibles de la ecuación de energía, y no de la ecuación de masas. En particular, la restricción incompresible corresponde a la siguiente ecuación de energía muy simple:

{De over Dt}=0

Así, para un fluido no viscoso e incompresible, la energía interna específica es constante a lo largo de las líneas de flujo, también en un flujo que depende del tiempo. La presión en un flujo incompresible actúa como un multiplicador de Lagrange, siendo el multiplicador de la restricción incompresible en la ecuación de energía, y en consecuencia en flujos incompresibles no tiene significado termodinámico. De hecho, la termodinámica es propia de flujos compresibles y degenera en flujos incompresibles.

Basándonos en la ecuación de conservación de la masa, se puede poner esta ecuación en la forma de conservación:

{partial rho e over partial t}+nabla cdot (rho emathbf {u})=0

lo que significa que para un flujo no conductor, invisible e incompresible, se cumple una ecuación de continuidad para la energía interna.

Conservación de entalpía

Ya que por definición la entalpía específica es:

h=e+{frac {p}{rho }}

La derivada material de la energía interna específica se puede expresar como:

{De over Dt}={Dh over Dt}-{frac {1}{rho }}left({Dp over Dt}-{frac {p}{rho }}{Drho over Dt}right)

Luego, sustituyendo la ecuación del momento en esta expresión, se obtiene:

{De over Dt}={Dh over Dt}-{frac {1}{rho }}left(pnabla cdot mathbf {u} +{Dp over Dt}right)

Y sustituyendo este último en la ecuación de energía, se obtiene que la expresión de entalpía para la ecuación de energía de Euler:

{Dh over Dt}={frac {1}{rho }}{Dp over Dt}

En un sistema de referencia que se mueve con un flujo no viscoso y no conductor, la variación de entalpía corresponde directamente a una variación de presión.

Termodinámica de fluidos ideales

En termodinámica las variables independientes son el volumen específico y la entropía específica, mientras que la energía específica es una función del estado de estas dos variables.

Deducción del formulario válido para sistemas termodinámicos

Considerando la primera ecuación, la variable debe cambiarse de densidad a volumen específico. Por definición:

vequiv {frac {1}{rho }}

Así, las siguientes identidades sostienen:

{displaystyle nabla rho =nabla left({frac {1}{v}}right)=-{frac {1}{v^{2}}}nabla v}

{displaystyle {frac {partial rho }{partial t}}={frac {partial }{partial t}}left({frac {1}{v}}right)=-{frac {1}{v^{2}}}{frac {partial v}{partial t}}}

Luego sustituyendo estas expresiones en la ecuación de conservación de masas:

{displaystyle -{frac {mathbf {u} }{v^{2}}}cdot nabla v-{frac {1}{v^{2}}}{frac {partial v}{partial t}}=-{frac {1}{v}}nabla cdot mathbf {u} }

Y por multiplicación:

{displaystyle {partial v over partial t}+mathbf {u} cdot nabla v=vnabla cdot mathbf {u} }

Esta ecuación es la única pertenencia a ecuaciones continuum generales, por lo que sólo esta ecuación tiene la misma forma por ejemplo también en las ecuaciones Navier-Stokes.

Por otro lado, la presión en la termodinámica es lo opuesto al derivado parcial de la energía interna específica con respecto al volumen específico:

{displaystyle p(v,s)=-{partial e(v,s) over partial v}}

ya que la energía interna en la termodinámica es una función de las dos variables antes mencionadas, el gradiente de presión contenido en la ecuación de impulso debe ser explícito como:

-nabla p(v,s)=-{frac {partial p}{partial v}}nabla v-{frac {partial p}{partial s}}nabla s={frac {partial ^{2}e}{partial v^{2}}}nabla v+{frac {partial ^{2}e}{partial vpartial s}}nabla s

Es conveniente para la brevedad cambiar la notación para los derivados del segundo orden:

-nabla p(v,s)=e_{vv}nabla v+e_{vs}nabla s

Finalmente, la ecuación energética:

{displaystyle {De over Dt}=-pvnabla cdot mathbf {u} }

se puede simplificar aún más en forma convectiva cambiando la variable de la energía específica a la entropía específica: de hecho la primera ley de la termodinámica en forma local se puede escribir:

{De over Dt}=T{Ds over Dt}-p{Dv over Dt}

sustituyendo el derivado material de la energía interna, la ecuación energética se convierte en:

{displaystyle T{Ds over Dt}+{frac {p}{rho ^{2}}}left({Drho over Dt}+rho nabla cdot mathbf {u} right)=0}

ahora el término entre paréntesis es idéntico cero según la conservación de la masa, entonces la ecuación de energía de Euler se convierte simplemente:

{Ds over Dt}=0

Para un fluido termodinámico, las ecuaciones de Euler compresibles se escriben mejor como:

Ecuaciones de Euler ()forma convectiva, para un sistema termodinámico)

${displaystyle left{{begin{aligned}{Dv over Dt}&=vnabla cdot mathbf {u} \[1.2ex]{frac {Dmathbf {u} }{Dt}}&=ve_{vv}nabla v+ve_{vs}nabla s+mathbf {g} \[1.2ex]{Ds over Dt}&=0end{aligned}}right.}$

donde:

$v$ es el volumen específico
$mathbf u$ es el vector de velocidad de flujo
$s$ es la entropía específica

En el caso general y no sólo en el caso incompresible, la ecuación de energía significa que para un fluido termodinámico no viscoso la entropía específica es constante a lo largo de las líneas de flujo, también en un flujo dependiente del tiempo. Basándose en la ecuación de conservación de la masa, se puede poner esta ecuación en la forma de conservación:

{partial rho s over partial t}+nabla cdot (rho smathbf {u})=0

lo que significa que para un flujo no conductor no viscoso se cumple una ecuación de continuidad para la entropía.

Por otro lado, las dos derivadas parciales de segundo orden de la energía interna específica en la ecuación del momento requieren la especificación de la ecuación de estado fundamental del material considerado, es decir, de la energía interna específica en función de las dos variables. volumen específico y entropía específica:

{displaystyle e=e(v,s)}

La ecuación de estado fundamental contiene toda la información termodinámica sobre el sistema (Callen, 1985), exactamente como el par de una ecuación de estado térmica junto con una ecuación de estado calórica.

Formulario de conservación

Las ecuaciones de Euler en el límite de Froude son equivalentes a una única ecuación de conservación con cantidad conservada y flujo asociado respectivamente:

{displaystyle {mathbf {y} }={begin{pmatrix}rho \mathbf {j} \E^{t}end{pmatrix}};qquad {mathbf {F} }={begin{pmatrix}mathbf {j} \{frac {1}{rho }}mathbf {j} otimes mathbf {j} +pmathbf {I} \left(E^{t}+pright){frac {1}{rho }}mathbf {j} end{pmatrix}}.}

donde:

${displaystyle mathbf {j} =rho mathbf {u} }$ es la densidad de impulso, una variable de conservación.
${textstyle E^{t}=rho e+{frac {1}{2}}rho u^{2}}$ es la densidad total de energía (energía total por volumen de unidad).

Aquí. $mathbf {y}$ tiene longitud N + 2 y $mathbf {F}$ tiene tamaño N(N + 2). En general (no sólo en el límite Froude) Las ecuaciones de Euler son expresables como:

Ecuaciones de Euler ()conservación original o forma euleria)

${displaystyle {frac {partial }{partial t}}{begin{pmatrix}rho \mathbf {j} \E^{t}end{pmatrix}}+nabla cdot {begin{pmatrix}mathbf {j} \{frac {1}{rho }}mathbf {j} otimes mathbf {j} +pmathbf {I} \left(E^{t}+pright){frac {1}{rho }}mathbf {j} end{pmatrix}}={begin{pmatrix}0\mathbf {f} \{frac {1}{rho }}mathbf {j} cdot mathbf {f} end{pmatrix}}}$

donde:

${displaystyle mathbf {f} =rho mathbf {g} }$ es la densidad de fuerza, una variable de conservación.

Observamos que también la ecuación de Euler, incluso cuando es conservadora (sin campo externo, límite de Froude), no tiene invariantes de Riemann en general. Se requieren algunas suposiciones adicionales

Sin embargo, ya mencionamos que para un fluido termodinámico la ecuación para la densidad de energía total es equivalente a la ecuación de conservación:

{partial over partial t}(rho s)+nabla cdot (rho smathbf {u})=0

Entonces las ecuaciones de conservación en el caso de un fluido termodinámico se expresan de manera más simple como:

Ecuaciones de Euler ()forma de conservación, para fluidos termodinámicos)

${displaystyle {frac {partial }{partial t}}{begin{pmatrix}rho \mathbf {j} \Send{pmatrix}}+nabla cdot {begin{pmatrix}mathbf {j} \{frac {1}{rho }}mathbf {j} otimes mathbf {j} +pmathbf {I} \S{frac {mathbf {j} }{rho }}end{pmatrix}}={begin{pmatrix}0\mathbf {f} \0end{pmatrix}}}$

donde:

$S=rho s$ es la densidad de entropía, una variable de conservación termodinámica.

Did you mean:

Another possible form for the energy equation, being particularly useful for isobaric, is:

{displaystyle {frac {partial H^{t}}{partial t}}+nabla cdot left(H^{t}mathbf {u} right)=mathbf {u} cdot mathbf {f} -{frac {partial p}{partial t}}}

donde:

${textstyle H^{t}=E^{t}+p=rho e+p+{frac {1}{2}}rho u^{2}}$ es la densidad total enthalpy.

Forma cuasilineal y ecuaciones características

La expansión de los flujos puede ser una parte importante de la construcción de solucionadores numéricos, por ejemplo, explotando soluciones (aproximadas) al problema de Riemann. En regiones donde el vector de estado y varía suavemente, las ecuaciones en forma conservadora se pueden expresar en forma cuasilineal:

{displaystyle {frac {partial mathbf {y} }{partial t}}+mathbf {A} _{i}{frac {partial mathbf {y} }{partial r_{i}}}={mathbf {0} }.}

Donde ${displaystyle mathbf {A} _{i}}$ son llamados el flujo Jacobianos definidos como las matrices:

{displaystyle mathbf {A} _{i}(mathbf {y})={frac {partial mathbf {f} _{i}(mathbf {y})}{partial mathbf {y} }}.}

Obviamente este Jacobiano no existe en las regiones de discontinuidad (por ejemplo, discontinuidades de contacto, ondas de choque en flujos no conductivos invisibles). Si el flujo Jacobians ${displaystyle mathbf {A} _{i}}$ no son funciones del vector estatal $mathbf {y}$ , las ecuaciones revela lineal.

Ecuaciones características

Las ecuaciones comprimibles de Euler se pueden desacoplar en un conjunto de ecuaciones de onda N+2 que describen el sonido en el continuo euleriano si se expresan en variables características en lugar de variables conservadas.

De hecho, el tensor A siempre es diagonalizable. Si los valores propios (el caso de las ecuaciones de Euler) son todos reales, el sistema se define hiperbólico y físicamente los valores propios representan las velocidades de propagación de la información. Si se distinguen todas, el sistema se define estrictamente hiperbólico (se demostrará que es el caso de las ecuaciones de Euler unidimensionales). Además, la diagonalización de la ecuación de Euler compresible es más fácil cuando la ecuación de energía se expresa en la variable entropía (es decir, con ecuaciones para fluidos termodinámicos) que en otras variables de energía. Esto quedará claro al considerar el caso 1D.

Si ${mathbf p}_{i}$ es el eigenvector derecho de la matriz $mathbf {A}$ correspondiente al eigenvalue $lambda _{i}$ , mediante la construcción de la matriz de proyección:

{displaystyle mathbf {P} =left[mathbf {p} _{1},mathbf {p} _{2},...,mathbf {p} _{n}right]}

Finalmente podemos encontrar las variables características como:

mathbf {w} =mathbf {P} ^{-1}mathbf {y}

Dado que A es constante, multiplicar la ecuación 1-D original en forma jacobiana de flujo por P⁻¹ produce las ecuaciones características:

{frac {partial w_{i}}{partial t}}+lambda _{j}{frac {partial w_{i}}{partial r_{j}}}=0_{i}

Las ecuaciones originales se han desacoplado en N+2 ecuaciones características, cada una de las cuales describe una onda simple, siendo los valores propios las velocidades de onda. Las variables w_i se denominan variables características y son un subconjunto de las variables conservadoras. La solución del problema del valor inicial en términos de variables características es finalmente muy sencilla. En una dimensión espacial es:

{displaystyle w_{i}(x,t)=w_{i}left(x-lambda _{i}t,0right)}

Entonces la solución en términos de las variables conservadoras originales se obtiene transformando nuevamente:

{displaystyle mathbf {y} =mathbf {P} mathbf {w}}

Did you mean:

this computation can be explicit as the linear combination of the eigenvectors:

{displaystyle mathbf {y} (x,t)=sum _{i=1}^{m}w_{i}left(x-lambda _{i}t,0right)mathbf {p} _{i},}

Ahora resulta evidente que las variables características actúan como pesos en la combinación lineal de los vectores propios jacobianos. La solución puede verse como una superposición de ondas, cada una de las cuales advecta independientemente sin cambiar de forma. Cada onda i-ésima tiene forma w_ip_i y velocidad de propagación λ_i. A continuación mostramos un ejemplo muy sencillo de este procedimiento de solución.

Ondas en fluido termodinámico 1D invisible y no conductor

Si se consideran las ecuaciones de Euler para un fluido termodinámico con los dos supuestos adicionales de una dimensión espacial y libre (sin campo externo: g = 0):

{displaystyle left{{begin{aligned}{partial v over partial t}+u{partial v over partial x}-v{partial u over partial x}&=0\[1.2ex]{partial u over partial t}+u{partial u over partial x}-e_{vv}v{partial v over partial x}-e_{vs}v{partial s over partial x}&=0\[1.2ex]{partial s over partial t}+u{partial s over partial x}&=0end{aligned}}right.}

Si se define el vector de variables:

{displaystyle mathbf {y} ={begin{pmatrix}v\u\send{pmatrix}}}

recordando que $v$ es el volumen específico, $u$ la velocidad de flujo, $s$ la entropía específica, la matriz jacobian correspondiente es:

{displaystyle {mathbf {A} }={begin{pmatrix}u&-v&0\-e_{vv}v&u&-e_{vs}v\0&0&uend{pmatrix}}.}

Al principio se deben encontrar los valores propios de esta matriz resolviendo la ecuación característica:

{displaystyle det(mathbf {A} (mathbf {y})-lambda (mathbf {y})mathbf {I})=0}

that is explicitly:

...

det {begin{bmatrix}u-lambda &-v&0\-e_{vv}v&u-lambda &-e_{vs}v\0&0&u-lambda end{bmatrix}}=0

Este determinante es muy simple: el cálculo más rápido comienza en la última fila, ya que tiene el mayor número de elementos cero.

(u-lambda)det {begin{bmatrix}u-lambda &-v\-e_{vv}v&u-lambda end{bmatrix}}=0

Ahora calculando el determinante 2×2:

{displaystyle (u-lambda)left((u-lambda)^{2}-e_{vv}v^{2}right)=0}

definiendo el parámetro:

a(v,s)equiv v{sqrt {e_{vv}}}

o equivalentemente en variables mecánicas, como:

a(rhop)equiv {sqrt {partial p over partial rho }}

Este parámetro siempre es real según la segunda ley de la termodinámica. De hecho, la segunda ley de la termodinámica se puede expresar mediante varios postulados. El más elemental de ellos en términos matemáticos es el enunciado de la convexidad de la ecuación de estado fundamental, es decir, la matriz de arpillera de la energía específica expresada en función del volumen específico y la entropía específica:

{begin{pmatrix}e_{vv}&e_{vs}\e_{vs}&e_{ss}end{pmatrix}}

se define como positivo. Esta afirmación corresponde a las dos condiciones:

0\[1.2ex]e_{vv}e_{ss}-e_{vs}^{2}&>0end{aligned}}right.}" xmlns="http://www.w3.org/1998/Math/MathML">{}evv■0evvess− − evs2■0{displaystyle left{begin{aligned}e_{vv} sentimiento0[1.2ex]e_{vv}e_{ss}-e_{vs}{2} {0end{aligned}}right.}0\[1.2ex]e_{vv}e_{ss}-e_{vs}^{2}&>0end{aligned}}right.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5c95b8e89f2d859f01c14c0697d666b320d599fe" style="vertical-align: -3.171ex; width:18.378ex; height:7.509ex;"/>

La primera condición es la que garantiza que el parámetro a sea real.

La ecuación característica finalmente resulta:

{displaystyle (u-lambda)left((u-lambda)^{2}-a^{2}right)=0}

Eso tiene tres soluciones reales:

lambda _{1}(v,u,s)=u-a(v,s)quad lambda _{2}(u)=u,quad lambda _{3}(v,u,s)=u+a(v,s)

Entonces la matriz tiene tres valores propios reales, todos distinguidos: las ecuaciones 1D de Euler son un sistema estrictamente hiperbólico.

En este punto se deben determinar los tres vectores propios: cada uno se obtiene sustituyendo un valor propio en la ecuación de valores propios y luego resolviéndolo. Sustituyendo el primer valor propio λ₁ se obtiene:

{begin{pmatrix}a&-v&0\-e_{vv}v&a&-e_{vs}v\0&0&aend{pmatrix}}{begin{pmatrix}v_{1}\u_{1}\s_{1}end{pmatrix}}=0

Basando en la tercera ecuación que simplemente tiene solución s₁=0, el sistema se reduce a:

{begin{pmatrix}a&-v\-a^{2}/v&aend{pmatrix}}{begin{pmatrix}v_{1}\u_{1}end{pmatrix}}=0

Las dos ecuaciones son redundantes como de costumbre, entonces el vector propio se define con una constante multiplicadora. Elegimos como vector propio derecho:

mathbf {p} _{1}={begin{pmatrix}v\a\0end{pmatrix}}

Los otros dos vectores propios se pueden encontrar con un procedimiento análogo al siguiente:

mathbf {p} _{2}={begin{pmatrix}e_{vs}\0\-left({frac {a}{v}}right)^{2}end{pmatrix}},qquad mathbf {p} _{3}={begin{pmatrix}v\-a\0end{pmatrix}}

Entonces se puede construir la matriz de proyección:

mathbf {P} (v,u,s)=(mathbf {p} _{1},mathbf {p} _{2},mathbf {p} _{3})={begin{pmatrix}v&e_{vs}&v\a&0&-a\0&-left({frac {a}{v}}right)^{2}&0end{pmatrix}}

Finalmente se hace evidente que el parámetro real a previamente definido es la velocidad de propagación de la información característica del sistema hiperbólico formado por las ecuaciones de Euler, es decir, es la velocidad de onda. Queda por demostrar que la velocidad del sonido corresponde al caso particular de una transformación isentrópica:

a_{s}equiv {sqrt {left({partial p over partial rho }right)_{s}}}

Compresibilidad y velocidad del sonido

Did you mean:

Sound speed is defined as the wave speed of an isentropic transformation:

a_{s}(rhop)equiv {sqrt {left({partial p over partial rho }right)_{s}}}

Did you mean:

by the definition of the isentropic compressibility:

K_{s}(rhop)equiv {frac {1}{rho }}left({partial p over partial rho }right)_{s}

la velocidad del sonido resulta siempre de la raíz cuadrada de la relación entre la compresibilidad isentrópica y la densidad:

a_{s}equiv {sqrt {frac {K_{s}}{rho }}}

Gas ideal

La velocidad del sonido en un gas ideal depende únicamente de su temperatura:

a_{s}(T)={sqrt {gamma {frac {T}{m}}}}

Deducción de la forma válida para gases ideales

En un gas ideal la transformación isoentropica es descrita por la ley Poisson:

{displaystyle dleft(prho ^{-gamma }right)_{s}=0}

Donde γ es la relación de capacidad de calor, una constante para el material. Expresando las diferencias:

rho ^{-gamma }(dp)_{s}+gamma prho ^{-gamma -1}(drho)_{s}=0

y dividiendo para ***^−γ d***:

{displaystyle left({partial p over partial rho }right)_{s}=gamma prho }

Luego, por sustitución en las definiciones generales para un gas ideal, la compresibilidad istrópica es simplemente proporcional a la presión:

K_{s}(p)=gamma p

y los resultados de la velocidad del sonido (Newton-Laplace law):

a_{s}(rhop)={sqrt {gamma {frac {p}{rho }}}}

Notablemente, para un gas ideal la ley de gas ideal sostiene, que en forma matemática es simplemente:

{displaystyle p=nT}

Donde n es la densidad número, y T es la temperatura absoluta, siempre que se mide en unidades energéticas (es decir, en joules) a través de la multiplicación con la constante Boltzmann. Puesto que la densidad de masa es proporcional a la densidad de número a través de la masa molecular media m del material:

rho =mn

La ley de gas ideal se puede replantear en la fórmula:

{frac {p}{rho }}={frac {T}{m}}

Sustituyendo esta proporción en la ley Newton-Laplace, finalmente se logra la expresión de la velocidad del sonido en un gas ideal como función de la temperatura.

Dado que la entalpía específica en un gas ideal es proporcional a su temperatura:

h=c_{p}T={frac {gamma }{gamma -1}}{frac {T}{m}}

La velocidad del sonido en un gas ideal también puede depender únicamente de su entalpía específica:

a_{s}(h)={sqrt {(gamma -1)h}}

Showing translation for

Bernoulli 's theorem for steady inviscid flow

Showing translation for

Bernoulli 's theorem is a direct consequence of the Euler equations.

Did you mean:

Incompressible case and Lamb 's form

La identidad del cálculo vectorial del producto cruzado de un rizo se cumple:

{displaystyle mathbf {v times } left(mathbf {nabla times F} right)=nabla _{F}left(mathbf {vcdot F} right)-mathbf {vcdot nabla } mathbf {F} }

donde la notación del subscripto Feynman $nabla _{F}$ se utiliza, lo que significa que el gradiente subscripto opera sólo en el factor $mathbf {F}$ .

Lamb en su famoso libro clásico Hidrodinámica (1895), aún impreso, utilizó esta identidad para cambiar el término convectivo de la velocidad del flujo en forma rotacional:

{displaystyle mathbf {u} cdot nabla mathbf {u} ={frac {1}{2}}nabla left(u^{2}right)+(nabla times mathbf {u})times mathbf {u} }

Did you mean:

the Euler momentum equation in Lamb 's form becomes:

{displaystyle {frac {partial mathbf {u} }{partial t}}+{frac {1}{2}}nabla left(u^{2}right)+(nabla times mathbf {u})times mathbf {u} +{frac {nabla p}{rho }}=mathbf {g} ={frac {partial mathbf {u} }{partial t}}+{frac {1}{2}}nabla left(u^{2}right)-mathbf {u} times (nabla times mathbf {u})+{frac {nabla p}{rho }}}

Ahora, basándonos en la otra identidad:

nabla left({frac {p}{rho }}right)={frac {nabla p}{rho }}-{frac {p}{rho ^{2}}}nabla rho

Did you mean:

the Euler momentum equation assumes a form that is optimal to demonstrate Bernoulli 's theorem for steady flows:

{displaystyle nabla left({frac {1}{2}}u^{2}+{frac {p}{rho }}right)-mathbf {g} =-{frac {p}{rho ^{2}}}nabla rho +mathbf {u} times (nabla times mathbf {u})-{frac {partial mathbf {u} }{partial t}}}

De hecho, en el caso de un campo conservador externo, definiendo su potencial φ:

{displaystyle nabla left({frac {1}{2}}u^{2}+phi +{frac {p}{rho }}right)=-{frac {p}{rho ^{2}}}nabla rho +mathbf {u} times (nabla times mathbf {u})-{frac {partial mathbf {u} }{partial t}}}

En el caso de un flujo constante, la derivada temporal de la velocidad del flujo desaparece, por lo que la ecuación del momento se convierte en:

{displaystyle nabla left({frac {1}{2}}u^{2}+phi +{frac {p}{rho }}right)=-{frac {p}{rho ^{2}}}nabla rho +mathbf {u} times (nabla times mathbf {u})}

Y al proyectar la ecuación del momento en la dirección del flujo, es decir, a lo largo de una línea de corriente, el producto vectorial desaparece porque su resultado es siempre perpendicular a la velocidad:

{displaystyle mathbf {u} cdot nabla left({frac {1}{2}}u^{2}+phi +{frac {p}{rho }}right)=-{frac {p}{rho ^{2}}}mathbf {u} cdot nabla rho }

En el caso estacionario e incompresible, la ecuación de masa es simplemente:

mathbf {u} cdot nabla rho =0

es decir, la conservación de masa para un flujo constante e incompresible establece que la densidad a lo largo de una línea de corriente es constante. Entonces la ecuación del momento de Euler en el caso estacionario e incompresible se convierte en:

mathbf {u} cdot nabla left({frac {1}{2}}u^{2}+phi +{frac {p}{rho }}right)=0

La conveniencia de definir la altura total para un flujo de líquido no viscoso ahora es evidente:

{displaystyle b_{l}equiv {frac {1}{2}}u^{2}+phi +{frac {p}{rho }},}

que puede escribirse simplemente como:

mathbf {u} cdot nabla b_{l}=0

Es decir, el balance de impulso para un flujo estable, no viscoso e incompresible en un campo conservador externo establece que la carga total a lo largo de una línea de corriente es constante.

Estuche comprimible

Did you mean:

In the most general steady (compressible) case the mass equation in conservation form is:

{displaystyle nabla cdot mathbf {j} =rho nabla cdot mathbf {u} +mathbf {u} cdot nabla rho =0}

Por lo tanto, la expresión anterior es más bien

{displaystyle mathbf {u} cdot nabla left({frac {1}{2}}u^{2}+phi +{frac {p}{rho }}right)={frac {p}{rho }}nabla cdot mathbf {u} }

El lado derecho aparece en la ecuación de energía en forma convectiva, que en estado estacionario dice:

{displaystyle mathbf {u} cdot nabla e=-{frac {p}{rho }}nabla cdot mathbf {u} }

Por lo tanto, la ecuación de energía se convierte en:

{displaystyle mathbf {u} cdot nabla left(e+{frac {p}{rho }}+{frac {1}{2}}u^{2}+phi right)=0,}

para que la energía interna específica ahora aparezca en la cabeza.

Dado que el potencial de campo externo suele ser pequeño comparado con los demás términos, conviene agrupar estos últimos en la entalpía total:

h^{t}equiv e+{frac {p}{rho }}+{frac {1}{2}}u^{2}

y el invariante de Bernoulli para un flujo de gas no viscoso es:

{displaystyle b_{g}equiv h^{t}+phi =b_{l}+e,}

que se puede escribir como:

mathbf {u} cdot nabla b_{g}=0

Es decir, el balance de energía para un flujo constante y no viscoso en un campo conservador externo establece que la suma de la entalpía total y el potencial externo es constante a lo largo de una línea de corriente.

En el caso habitual de un campo potencial pequeño, simplemente:

mathbf {u} cdot nabla h^{t}sim 0

Forma Friedmann y forma Crocco

Sustituyendo el gradiente de presión por el gradiente de entropía y entalpía, según la primera ley de la termodinámica en la forma de entalpía:

vnabla p=-Tnabla s+nabla h

en la forma convectiva de la ecuación del momento de Euler, se llega a:

{frac {Dmathbf {u} }{Dt}}=Tnabla ,s-nabla ,h

Friedmann dedujo esta ecuación para el caso particular de un gas perfecto y la publicó en 1922. Sin embargo, esta ecuación es general para un fluido no viscoso no conductor y no contiene ninguna ecuación de estado implícita.

Por otro lado, al sustituir la forma de entalpía de la primera ley de la termodinámica en la forma rotacional de la ecuación del momento de Euler, se obtiene:

{displaystyle {frac {partial mathbf {u} }{partial t}}+{frac {1}{2}}nabla left(u^{2}right)+(nabla times mathbf {u})times mathbf {u} +{frac {nabla p}{rho }}=mathbf {g} }

y definiendo la entalpía total específica:

{displaystyle h^{t}=h+{frac {1}{2}}u^{2}}

se llega a la forma de Crocco-Vazsonyi (Crocco, 1937) de la ecuación del momento de Euler:

{frac {partial mathbf {u} }{partial t}}+(nabla times mathbf {u})times mathbf {u} -Tnabla s+nabla h^{t}=mathbf {g}

Did you mean:

In the steady case the two variables entropy and total enthalpy are particularly useful since Euler equations can be recast into the Crocco 's form:

{displaystyle left{{begin{aligned}mathbf {u} times nabla times mathbf {u} +Tnabla s-nabla h^{t}&=mathbf {g} \mathbf {u} cdot nabla s&=0\mathbf {u} cdot nabla h^{t}&=0end{aligned}}right.}

Finalmente si el flujo también es isotérmico:

Tnabla s=nabla (Ts)

definiendo la energía libre de Gibbs total específica:

g^{t}equiv h^{t}+Ts

Did you mean:

the Crocco 's form can be reduced to:

{displaystyle left{{begin{aligned}mathbf {u} times nabla times mathbf {u} -nabla g^{t}&=mathbf {g} \mathbf {u} cdot nabla g^{t}&=0end{aligned}}right.}

Did you mean:

From these relationships one deduces that the specific total free energy is uniform in a steady, irrotational, isothermal, isentropic, inviscid flow.

Discontinuidades

Las ecuaciones de Euler son ecuaciones hiperbólicas cuasilineales y sus soluciones generales son ondas. Bajo ciertos supuestos, se pueden simplificar y conducir a la ecuación de Burgers. Al igual que las conocidas olas oceánicas, las ondas descritas por las ecuaciones de Euler "rompen" el océano. y se forman las llamadas ondas de choque; este es un efecto no lineal y representa que la solución se vuelve multivaluada. Físicamente, esto representa una ruptura de los supuestos que llevaron a la formulación de las ecuaciones diferenciales, y para extraer más información de las ecuaciones debemos volver a la forma integral más fundamental. Luego, se formulan soluciones débiles trabajando en 'saltos' (discontinuidades) en las cantidades de flujo (densidad, velocidad, presión, entropía) utilizando las ecuaciones de Rankine-Hugoniot. Las cantidades físicas rara vez son discontinuas; en flujos reales, estas discontinuidades se suavizan mediante la viscosidad y la transferencia de calor. (Ver ecuaciones de Navier-Stokes)

La propagación de impactos se estudia, entre muchos otros campos, en la aerodinámica y la propulsión de cohetes, donde se producen flujos suficientemente rápidos.

Para calcular adecuadamente las cantidades continuas en zonas discontinuas (por ejemplo, ondas de choque o capas límite) a partir de las formas locales (todas las formas anteriores son formas locales, ya que las variables que se describen son típicas de una punto en el espacio considerado, es decir, son variables locales) de las ecuaciones de Euler mediante métodos de diferencias finitas, generalmente serían necesarios demasiados puntos espaciales y pasos de tiempo para la memoria de las computadoras ahora y en el futuro cercano. En estos casos es obligatorio evitar las formas locales de las ecuaciones de conservación, pasando algunas formas débiles, como la de volumen finito.

Ecuaciones de Rankine-Hugoniot

A partir del caso más simple, se considera una ecuación de conservación libre y estable en forma de conservación en el dominio espacial:

nabla cdot mathbf {F} =mathbf {0}

donde en general F es la matriz de flujo. Al integrar esta ecuación local sobre un volumen fijo V_m, se convierte en:

{displaystyle int _{V_{m}}nabla cdot mathbf {F} ,dV=mathbf {0}.}

Entonces, basándonos en el teorema de la divergencia, podemos transformar esta integral en una integral de frontera del flujo:

{displaystyle oint _{partial V_{m}}mathbf {F} ,ds=mathbf {0}.}

Esta forma global simplemente establece que no hay un flujo neto de una cantidad conservada que pase a través de una región en el caso de que sea estable y sin fuente. En 1D el volumen se reduce a un intervalo, siendo su límite sus extremos, luego el teorema de la divergencia se reduce al teorema fundamental del cálculo:

{displaystyle int _{x_{m}}^{x_{m+1}}mathbf {F} (x'),dx'=mathbf {0}}

esa es la ecuación en diferencias finitas simple, conocida como relación de salto:

{displaystyle Delta mathbf {F} =mathbf {0}.}

Eso se puede hacer explícito como:

{displaystyle mathbf {F} _{m+1}-mathbf {F} _{m}=mathbf {0} }

donde la notación empleada es:

{displaystyle mathbf {F} _{m}=mathbf {F} (x_{m}).}

O, si se realiza una integral indefinida:

{displaystyle mathbf {F} -mathbf {F} _{0}=mathbf {0}.}

Por otro lado, una ecuación de conservación transitoria:

{partial y over partial t}+nabla cdot mathbf {F} =mathbf {0}

lleva a una relación de salto:

{displaystyle {frac {dx}{dt}},Delta u=Delta mathbf {F}.}

Para ecuaciones de Euler unidimensionales las variables de conservación y el flujo son los vectores:

{displaystyle mathbf {y} ={begin{pmatrix}{frac {1}{v}}\j\E^{t}end{pmatrix}},}

{displaystyle mathbf {F} ={begin{pmatrix}j\vj^{2}+p\vjleft(E^{t}+pright)end{pmatrix}},}

donde:

$v$ es el volumen específico,
$j$ es el flujo de masa.

En el caso unidimensional, las relaciones de salto correspondientes, denominadas ecuaciones de Rankine-Hugoniot, son:<

{displaystyle left{{begin{aligned}{frac {dx}{dt}}Delta left({frac {1}{v}}right)&=Delta j\[1.2ex]{frac {dx}{dt}}Delta j&=Delta (vj^{2}+p)\[1.2ex]{frac {dx}{dt}}Delta E^{t}&=Delta (jv(E^{t}+p))end{aligned}}right..}

En el caso unidimensional estable, el resultado es simplemente:

{displaystyle left{{begin{aligned}Delta j&=0\[1.2ex]Delta left(vj^{2}+pright)&=0\[1.2ex]Delta left(jleft({frac {E^{t}}{rho }}+{frac {p}{rho }}right)right)&=0end{aligned}}right..}

Gracias a la ecuación en diferencia de masas, la ecuación en diferencia de energía se puede simplificar sin ninguna restricción:

{displaystyle left{{begin{aligned}Delta j&=0\[1.2ex]Delta left(vj^{2}+pright)&=0\[1.2ex]Delta h^{t}&=0end{aligned}}right.,}

Donde $h^{t}$ es el enthalpy total específico.

Estas son las que suelen expresarse en las variables convectivas:

{displaystyle left{{begin{aligned}Delta j&=0\[1.2ex]Delta left({frac {u^{2}}{v}}+pright)&=0\[1.2ex]Delta left(e+{frac {1}{2}}u^{2}+pvright)&=0end{aligned}}right.,}

donde:

$u$ es la velocidad de flujo
$e$ es la energía interna específica.

La ecuación de energía es una forma integral de la ecuación de Bernoulli en el caso compresible. Las anteriores ecuaciones de masa y momento por sustitución conducen a la ecuación de Rayleigh:

{displaystyle {frac {Delta p}{Delta v}}=-{frac {u_{0}^{2}}{v_{0}}}.}

Dado que el segundo término es una constante, la ecuación de Rayleigh siempre describe una línea simple en el plano de presión-volumen que no depende de ninguna ecuación de estado, es decir, la línea de Rayleigh. Por sustitución en las ecuaciones de Rankine-Hugoniot, eso también puede hacerse explícito como:

{displaystyle left{{begin{aligned}rho u&=rho _{0}u_{0}\[1.2ex]rho u^{2}+p&=rho _{0}u_{0}^{2}+p_{0}\[1.2ex]e+{frac {1}{2}}u^{2}+{frac {p}{rho }}&=e_{0}+{frac {1}{2}}u_{0}^{2}+{frac {p_{0}}{rho _{0}}}end{aligned}}right..}

También se puede obtener la ecuación cinética y la ecuación de Hugoniot. Los pasajes analíticos no se muestran aquí por motivos de brevedad.

Estos son respectivamente:

{displaystyle left{{begin{aligned}u^{2}(v,p)&=u_{0}^{2}+(p-p_{0})(v_{0}+v)\[1.2ex]e(v,p)&=e_{0}+{frac {1}{2}}(p+p_{0})(v_{0}-v)end{aligned}}right..}

La ecuación de Hugoniot, junto con la ecuación fundamental de estado del material:

e=e(v,p)

describe en general en el plano presión-volumen una curva que pasa por las condiciones (v₀, p₀), es decir, la curva de Hugoniot, cuya forma depende en gran medida de la tipo de material considerado.

También es habitual definir una función Hugoniot:

{displaystyle {mathfrak {h}}(v,s)equiv e(v,s)-e_{0}+{frac {1}{2}}(p(v,s)+p_{0})(v-v_{0})}

permitiendo cuantificar las desviaciones de la ecuación de Hugoniot, de manera similar a la definición anterior de cabeza hidráulica, útil para las desviaciones de la ecuación de Bernoulli.

Forma de volumen finito

Por otro lado, integrando una ecuación de conservación genérica:

{displaystyle {frac {partial mathbf {y} }{partial t}}+nabla cdot mathbf {F} =mathbf {s} }

en un volumen fijo V_m, y luego basándose en el teorema de la divergencia, se convierte en:

{displaystyle {frac {d}{dt}}int _{V_{m}}mathbf {y} dV+oint _{partial V_{m}}mathbf {F} cdot {hat {n}}ds=mathbf {S}.}

Al integrar esta ecuación también en un intervalo de tiempo:

{displaystyle int _{V_{m}}mathbf {y} (mathbf {r}t_{n+1}),dV-int _{V_{m}}mathbf {y} (mathbf {r}t_{n}),dV+int _{t_{n}}^{t_{n+1}}oint _{partial V_{m}}mathbf {F} cdot {hat {n}},ds,dt=mathbf {0}.}

Ahora, definiendo la cantidad conservada del nodo:

{displaystyle mathbf {y} _{m,n}equiv {frac {1}{V_{m}}}int _{V_{m}}mathbf {y} (mathbf {r}t_{n}),dV,}

deducimos la forma del volumen finito:

{displaystyle mathbf {y} _{m,n+1}=mathbf {y} _{m,n}-{frac {1}{V_{m}}}int _{t_{n}}^{t_{n+1}}oint _{partial V_{m}}mathbf {F} cdot {hat {n}},ds,dt.}

En particular, para las ecuaciones de Euler, una vez determinadas las cantidades conservadas, las variables convectivas se deducen mediante sustitución inversa:

{displaystyle left{{begin{aligned}mathbf {u} _{m,n}&={frac {mathbf {j} _{m,n}}{rho _{m,n}}}\[1.2ex]e_{m,n}&={frac {E_{m,n}^{t}}{rho _{m,n}}}-{frac {1}{2}}u_{m,n}^{2}\[1.2ex]end{aligned}}right..}

Entonces las expresiones explícitas de volumen finito de las variables convectivas originales son:<

Ecuaciones de Euler ()Forma de volumen finito)

${displaystyle left{{begin{aligned}rho _{m,n+1}&=rho _{m,n}-{frac {1}{V_{m}}}int _{t_{n}}^{t_{n+1}}oint _{partial V_{m}}rho mathbf {u} cdot {hat {n}},ds,dt\[1.2ex]mathbf {u} _{m,n+1}&=mathbf {u} _{m,n}-{frac {1}{rho _{m,n}V_{m}}}int _{t_{n}}^{t_{n+1}}oint _{partial V_{m}}(rho mathbf {u} otimes mathbf {u} -pmathbf {I})cdot {hat {n}},ds,dt\[1.2ex]mathbf {e} _{m,n+1}&=mathbf {e} _{m,n}-{frac {1}{2}}left(u_{m,n+1}^{2}-u_{m,n}^{2}right)-{frac {1}{rho _{m,n}V_{m}}}int _{t_{n}}^{t_{n+1}}oint _{partial V_{m}}left(rho e+{frac {1}{2}}rho u^{2}+pright)mathbf {u} cdot {hat {n}},ds,dt\[1.2ex]end{aligned}}right..}$

Restricciones

Se ha demostrado que las ecuaciones de Euler no son un conjunto completo de ecuaciones, pero requieren algunas restricciones adicionales para admitir una solución única: se trata de la ecuación de estado del material considerado. Para ser consistentes con la termodinámica, estas ecuaciones de estado deberían satisfacer las dos leyes de la termodinámica. Por otro lado, por definición, los sistemas de desequilibrio se describen por leyes que se encuentran fuera de estas leyes. A continuación enumeramos algunas ecuaciones de estado muy simples y la influencia correspondiente en las ecuaciones de Euler.

Gas politrópico ideal

Para un gas politrópico ideal, la ecuación de estado fundamental es:

{displaystyle e(v,s)=e_{0}e^{(gamma -1)mleft(s-s_{0}right)}left({v_{0} over v}right)^{gamma -1}}

Donde $e$ es la energía específica, $v$ es el volumen específico, $s$ es la entropía específica, $m$ es la masa molecular, $gamma$ aquí se considera una constante (proceso polímico), y se puede demostrar que corresponde a la relación de capacidad de calor. Esta ecuación se puede demostrar que es consistente con las ecuaciones habituales de estado empleadas por la termodinámica.

Demostración de la consistencia con la termodinámica de un gas ideal

Por la definición termodinámica de la temperatura:

T(e)equiv {partial e over partial s}=(gamma -1)me

Donde la temperatura se mide en unidades de energía. Al principio, note que al combinar estas dos ecuaciones se puede deducir las Derecho de gas ideal:

pv=mT

o, en la forma habitual:

p=nT

Donde: $nequiv {frac {m}{v}}$ es la densidad número del material. Por otro lado, la ley de gas ideal es menos estricta que la ecuación fundamental original de estado considerada.

Ahora considere la capacidad de calor molar asociada a un proceso x:

c_{x}=left(mT{partial s over partial T}right)_{x}

según la primera ley de la termodinámica:

{displaystyle de(v,s)=-pdv+T,ds}

se puede simplemente expresar como:

c_{x}equiv mleft({partial e over partial T}right)_{x}+mpleft({partial v over partial T}right)_{x}

Ahora invirtiendo la ecuación para la temperatura T(e) deducimos que para un gas politrópico ideal la capacidad de calor isocópico es una constante:

c_{v}equiv mleft({partial e over partial T}right)_{v}=m{de over dT}={frac {1}{(gamma -1)}}

y de forma similar para un gas politrópico ideal, la capacidad de calor isobarico resulta constante:

c_{p}equiv mleft({partial e over partial T}right)_{p}+mpleft({partial v over partial T}right)_{p}=m{de over dT}+pleft({partial v over partial T}right)_{p}={frac {1}{(gamma -1)}}+1

Esto trae a dos relaciones importantes entre las capacidades de calor: la gamma constante representa realmente la ratio de capacidad térmica en el gas politrópico ideal:

{frac {c_{p}}{c_{v}}}=gamma

y uno también llega al La relación de Meyer:

c_{p}=c_{v}+1

La energía específica es entonces, invirtiendo la relación T(e):

e(T)={frac {mT}{gamma -1}}=c_{v}mT

Los resultados específicos por sustitución de este último y de la ley de gas ideal:

h(T)equiv e(T)+(pv)(T)=c_{v}mT+mT=c_{p}mT

De esta ecuación se puede derivar la ecuación de la presión según su definición termodinámica:

p(v,e)equiv -{partial e over partial v}=(gamma -1){frac {e}{v}}

Invirtiéndola se llega a la ecuación de estado mecánica:

e(v,p)={frac {pv}{gamma -1}}

Entonces, para un gas ideal, las ecuaciones de Euler compresibles se pueden expresar simplemente en las variables mecánicas o primitivas de volumen, velocidad de flujo y presión específicos, tomando el conjunto de las ecuaciones para un sistema termodinámico y modificar la ecuación de energía en una ecuación de presión a través de esta ecuación de estado mecánica. Finalmente, en forma convectiva resultan:

Ecuaciones Euler para un gas politrópico ideal ()forma convectiva)

${displaystyle left{{begin{aligned}{Dv over Dt}&=vnabla cdot mathbf {u} \[1.2ex]{frac {Dmathbf {u} }{Dt}}&=vnabla p+mathbf {g} \[1.2ex]{Dp over Dt}&=-gamma pnabla cdot mathbf {u} end{aligned}}right.}$

y en forma cuasilineal unidimensional resulta:

{displaystyle {frac {partial mathbf {y} }{partial t}}+mathbf {A} {frac {partial mathbf {y} }{partial x}}={mathbf {0} }.}

donde la variable vectorial conservadora es:

{displaystyle {mathbf {y} }={begin{pmatrix}v\u\pend{pmatrix}}}

y la matriz jacobiana correspondiente es:

{displaystyle {mathbf {A} }={begin{pmatrix}u&-v&0\0&u&v\0&gamma p&uend{pmatrix}}.}

Flujo constante en coordenadas de material

En el caso de flujo estacionario, es conveniente elegir el marco de Frenet-Serret a lo largo de una línea de corriente como sistema de coordenadas para describir la ecuación de Euler del momento estacionario:

{boldsymbol {u}}cdot nabla {boldsymbol {u}}=-{frac {1}{rho }}nabla p,

Donde $mathbf u$ , $p$ y $rho$ denota la velocidad de flujo, la presión y la densidad, respectivamente.

Vamos ${displaystyle left{mathbf {e} _{s},mathbf {e} _{n},mathbf {e} _{b}right}}$ ser una base ortonormal Frenet-Serret que consiste en un vector de unidad tangencial, un vector de unidad normal y un vector de unidad binormal a la velocidad, respectivamente. Como una aerodinámica es una curva que es tangente al vector de velocidad del flujo, el lado izquierdo de la ecuación anterior, el derivado convectivo de la velocidad, se puede describir como sigue:

{displaystyle {begin{aligned}{boldsymbol {u}}cdot nabla {boldsymbol {u}}\&=u{frac {partial }{partial s}}(u{boldsymbol {e}}_{s})&({boldsymbol {u}}=u{boldsymbol {e}}_{s},~{partial /partial s}equiv {boldsymbol {e}}_{s}cdot nabla)\&=u{frac {partial u}{partial s}}{boldsymbol {e}}_{s}+{frac {u^{2}}{R}}{boldsymbol {e}}_{n}&(because ~{frac {partial {boldsymbol {e}}_{s}}{partial s}}={frac {1}{R}}{boldsymbol {e}}_{n}),end{aligned}}}

Donde $R$ es el radio de curvatura de la aerodinámica.

Por lo tanto, se encuentra que la parte del momento de las ecuaciones de Euler para un flujo estacionario tiene una forma simple:

{displaystyle {begin{cases}displaystyle u{frac {partial u}{partial s}}=-{frac {1}{rho }}{frac {partial p}{partial s}},\displaystyle {u^{2} over R}=-{frac {1}{rho }}{frac {partial p}{partial n}}&({partial /partial n}equiv {boldsymbol {e}}_{n}cdot nabla),\displaystyle 0=-{frac {1}{rho }}{frac {partial p}{partial b}}&({partial /partial b}equiv {boldsymbol {e}}_{b}cdot nabla).end{cases}}}

Para el flujo barotrópico $(rho =rho (p))$ , la ecuación de Bernoulli se deriva de la primera ecuación:

{displaystyle {frac {partial }{partial s}}left({frac {u^{2}}{2}}+int {frac {mathrm {d} p}{rho }}right)=0.}

La segunda ecuación expresa que, en el caso de que la línea de corriente sea curva, debería existir un gradiente de presión normal a la línea de corriente porque la aceleración centrípeta de la parcela de fluido solo se genera por el gradiente de presión normal.

La tercera ecuación expresa que la presión es constante a lo largo del eje binormal.

Teorema de la curvatura aerodinámica

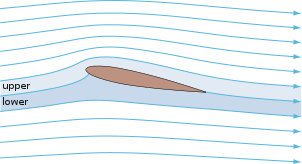
Vamos $r$ ser la distancia del centro de curvatura de la aerodinámica, entonces la segunda ecuación está escrita como sigue:

0),}" xmlns="http://www.w3.org/1998/Math/MathML">∂ ∂ p∂ ∂ r=*** *** u2r()■0),{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} p}{partial ¿Qué?0)," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6a8cfc762c0f0d6e3c04ae2c772322b1e40d23e3" style="vertical-align: -2.005ex; width:17.497ex; height:5.843ex;"/>

Donde ${partial /partial r}=-{partial /partial n}.$

Esta ecuación establece:

En un flujo constante de un fluido invisivo sin fuerzas externas, el centro de curvatura de la aerodinámica se encuentra en la dirección de disminuir la presión radial.

Aunque esta relación entre el campo de presión y la curvatura del flujo es muy útil, no tiene nombre en la literatura científica de habla inglesa. Los especialistas en dinámica de fluidos japoneses llaman a esta relación el "teorema de la curvatura de la línea aerodinámica".

Este "teorema" explica claramente por qué hay presiones tan bajas en el centro de los vórtices, que consisten en círculos concéntricos de líneas de corriente. Esta también es una forma de explicar intuitivamente por qué los perfiles aerodinámicos generan fuerzas de sustentación.

Soluciones exactas

Todas las soluciones de flujo potencial son también soluciones de las ecuaciones de Euler y, en particular, de las ecuaciones de Euler incompresibles cuando el potencial es armónico.

Las soluciones a las ecuaciones de Euler con vorticidad son:

flujos paralelos – donde el flujo es unidireccional, y la velocidad de flujo sólo varía en las direcciones de flujo cruzado, por ejemplo en un sistema de coordenadas cartesiano $(x,y,z)$ el flujo es por ejemplo en el $x$ -dirección - con el único componente de velocidad no cero ${displaystyle u_{x}(y,z)}$ sólo depende de $y$ y $z$ y no $x.$
Arnold–Beltrami–Childress flow – una solución exacta de las ecuaciones de Euler incompresibles.
Dos soluciones de las ecuaciones tridimensionales de Euler con simetría cilíndrica han sido presentadas por Gibbon, Moore y Stuart en 2003. Estas dos soluciones tienen energía infinita; explotan por todas partes en el espacio en tiempo finito.

Contenido relacionado

Más resultados...