Ecuación de Swain-Lupton

En química orgánica física, la ecuación de Swain-Lupton es una relación lineal de energía libre (LFER) que se utiliza en el estudio de los mecanismos de reacción y en el desarrollo de relaciones cuantitativas de estructura y actividad para compuestos orgánicos. Fue desarrollado por C. Gardner Swain y Elmer C. Lupton Jr. en 1968 como un refinamiento de la ecuación de Hammett para incluir tanto efectos de campo como efectos de resonancia.

Fondo

En química orgánica, el gráfico de Hammett proporciona un medio para evaluar los efectos de los sustituyentes en el equilibrio o la velocidad de una reacción utilizando la ecuación de Hammett (1):

(1)

Hammett desarrolló esta ecuación a partir de las constantes de equilibrio de la disociación del ácido benzoico y sus derivados (Fig. 1):

Fig. 1 Disociación de ácidos benzoicos sustituidos.

Hammett definió la ecuación basándose en dos parámetros: la constante de reacción (ρ) y el parámetro del sustituyente (σ). Cuando se estudiaron otras reacciones utilizando estos parámetros, no siempre se encontró una correlación debido a la derivación específica de estos parámetros del equilibrio de disociación de los ácidos benzoicos sustituidos y la negligencia original de los efectos de resonancia. Por lo tanto, los efectos de los sustituyentes en una serie de compuestos deben estudiarse en base a una reacción individual utilizando la ecuación derivada de Hammett para los efectos de campo o de resonancia, pero no para ambos.

Redefiniendo la ecuación

C. Gardner Swain y Elmer C. Lupton Jr. del Instituto Tecnológico de Massachusetts redefinieron el parámetro sustituyente, σ, basándose en la idea de que no son necesarias más de dos variables (efectos de resonancia y efectos de campo) para describir los efectos de cualquier sustituyente Los efectos de campo, F, se definen para incluir todos los efectos (inductivos y de campo puro). Asimismo, los efectos debidos a la resonancia, R, se deben al promedio de la capacidad de donación de electrones y la capacidad de aceptación de electrones. Se supone que estos dos efectos son independientes entre sí y, por lo tanto, se pueden escribir como una combinación lineal:

(2)

Estos dos parámetros se tratan como términos independientes debido a la suposición que hicieron Swain y Lupton; el sustituyente se mantiene distante por tres o más centros saturados o si el sustituyente es (CH ₃) ₃ N. Todos los demás términos son despreciables y conducen a la ecuación de Swain-Lupton (2).

El nuevo parámetro sustituyente

El parámetro del sustituyente ahora se define por los efectos de campo y resonancia, F y R, que dependen del sustituyente individual. Las constantes r y f explican la importancia de cada uno de los dos efectos. Estas constantes no dependen del sustituyente, sino que dependen del conjunto de parámetros del sustituyente de Hammett (σ, σ, σ, σ, etc.).

Para encontrar las constantes ponderadas, r y f, para cada conjunto de parámetros sustituyentes, sería necesario establecer el hecho de que cada nuevo parámetro sustituyente σ _X podría escribirse como una combinación lineal de parámetros sustituyentes de reacción específicos, es decir

(3)

donde σ _1X y σ _2X son parámetros de sustituyentes específicos (es decir, σ, σ, etc.) y c ₁ y c ₂ son constantes independientes del sustituyente (dependen de las condiciones de reacción, es decir, temperatura, solvente y reacción individual que se está estudiando). Esto se puede expresar de manera más genérica como:

(4)

donde i es una intersección para evitar fijar el origen en (0,0). Si esto no se hiciera, la ecuación daría mucho más peso a los compuestos no sustituidos con los que uno está tratando de hacer una comparación usando esta ecuación. Se usa un análisis de mínimos cuadrados lineales para determinar los coeficientes/constantes a, b e i (Swain y Lupton usaron un procedimiento llamado DOVE: evaluación de vector obligado doble). Las constantes se basaron primero en tres reacciones previas (σ, σ, σ), lo que conduce a más posibles errores ya que los datos compilados son solo una combinación mínima de un grupo mucho más grande. Al ver un posible error en este grupo limitado, el grupo de datos se incrementó asignando una escala para empezar. Se utiliza una escala cero para el hidrógeno, porque se sabe que no dona ni acepta fácilmente la densidad de electrones cuando se une a un átomo de carbono debido a electronegatividades similares. Se asignó un valor de 1 al NO ₂, porque investigaciones previas determinaron que el efecto de este sustituyente se debía predominantemente a la resonancia. Por último, F se igualó a R para ambos componentes para que los efectos de campo pudieran compararse directamente con los efectos de resonancia. Esto entonces conduce a:F = R = 0 para H (Hidrógeno).F = R = 1 para NO ₂ (dióxido de nitrógeno).

La figura 2 muestra algunos valores relativos de F y R que fundaron Swain y Lupton.

Categorías de sustituyentes

Los grupos alquilo tienen un valor de bajo a cero para F pero valores sensibles para R. Esto se explica más comúnmente por la hiperconjugación, lo que significa poco o ningún efecto inductivo pero efectos de resonancia parcial.

Fig. 2a Valores de F para sustituyentes comunes.

CF ₃ tiene una relación R / F mucho más alta que otros sustituyentes con altos grados de conjugación. Esto fue estudiado con mayor detalle por Swain, pero aún se explica mejor mediante la hiperconjugación de fluoruro.

Fig. 2b Valores R para sustituyentes comunes.

Los sustituyentes con carga positiva (es decir, N(CH ₃) y S(CH ₃)) tienen valores F positivos más grandes debido a una carga positiva que está saturada cerca de la estructura de carbono en cuestión. Los sustituyentes cargados negativamente (es decir, CO y SO) tienen valores de F mucho más bajos debido a su capacidad para hacer resonar la densidad de electrones entre los átomos de oxígeno y estabilizarla mediante enlaces de hidrógeno con solventes.

Las relaciones lineales de energía libre siguen siendo útiles, a pesar de sus desventajas cuando se las lleva al límite. Las nuevas técnicas para resolver los parámetros de los sustituyentes de Swain-Lupton implican el estudio de los cambios químicos a través de la espectroscopia de resonancia magnética nuclear. Recientemente, se estudiaron los cambios químicos N NMR y los efectos sustituyentes de 1,2,3,4,5,6,7,8-octahidroacridina y derivados. Se encontraron valores para R y F para el grupo −N(COCH ₃) ₂, que no se pudieron encontrar previamente usando métodos conocidos.

Valores de f y r

A veces es útil observar el porcentaje de resonancia (% r), porque r depende de la reacción y es el mismo para todos los sustituyentes.

(5)

Uno puede predecir la diferencia en los datos comparando dos sustituyentes usando % r:

(6)

El efecto más dominante es claro cuando se observa la relación de R a F. Por ejemplo, se demostró que un complejo de tungsteno alquila los carbonatos de alilo A y B. La relación de los productos A1 y B1 se puede atribuir al sustituyente para, X (Fig. 3). Utilizando los parámetros de Swain-Lupton (σ = 0,2 F + 0,8 R), se encontró que la pendiente era un valor de ρ de -2,5.

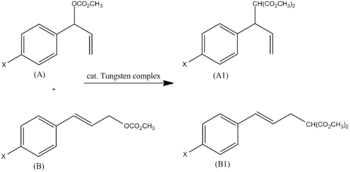
Fig. 3a Alquilación alílica de carbonatos.

Fig. 3b Gráfico de parámetros de Swain-Lupton.

Esto está de acuerdo con el mecanismo propuesto (se forma una carga positiva en el carbono bencílico y se estabiliza por resonancia; R domina en una proporción de 0,8/0,2).

Desventajas

Como cualquier otra relación lineal de energía libre establecida, la ecuación de Swain-Lupton también fallará cuando surjan circunstancias especiales, es decir, un cambio en el paso determinante de la velocidad de un mecanismo o estructura de solvatación.