Ecuación de Sellmeier

Índice refractivo vs longitud de onda para vidrio BK7, mostrando puntos medidos (cruces azules) y la ecuación Sellmeier (línea roja)

Igual que el gráfico anterior, pero con la ecuación de Cauchy (línea azul) para la comparación. Mientras que la ecuación de Cauchy (línea azul) se desvía significativamente de los índices refractivos medidos fuera de la región visible (que es color rojo sombreado), la ecuación de Sellmeier (línea verde rayada) no lo hace.

La ecuación de Sellmeier es una relación empírica entre el índice de refracción y la longitud de onda para un medio transparente particular. La ecuación se utiliza para determinar la dispersión de la luz en el medio.

Lo propuso por primera vez en 1872 Wolfgang Sellmeier y fue un desarrollo del trabajo de Augustin Cauchy sobre la ecuación de Cauchy para modelar la dispersión.

La ecuación

En su forma original y más general, la ecuación de Sellmeier se da como

n2()λ λ )=1+.. iBiλ λ 2λ λ 2− − Ci{displaystyle n^{2}(lambda)=1+sum _{i}{frac {B_{i}lambda ^{2}{lambda.,

donde n es el índice de refracción, λ es la longitud de onda y B_i y C_i son coeficientes de Sellmeier determinados experimentalmente. Estos coeficientes se suelen citar para λ en micrómetros. Tenga en cuenta que este λ es la longitud de onda del vacío, no la del material en sí, que es λ/n. A veces se usa una forma diferente de la ecuación para ciertos tipos de materiales, p. cristales

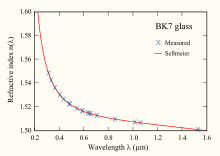
Cada término de la suma representa una resonancia de absorción de fuerza B_i en una longitud de onda √ C_i. Por ejemplo, los coeficientes para BK7 a continuación corresponden a dos resonancias de absorción en el ultravioleta y una en la región del infrarrojo medio. Cerca de cada pico de absorción, la ecuación da valores no físicos de n² = ±∞, y en estas regiones de longitud de onda un modelo de dispersión más preciso como Helmholtz's debe ser utilizado.

Si se especifican todos los términos para un material, en longitudes de onda largas lejos de los picos de absorción, el valor de n tiende a

n.. 1+.. iBi.. ε ε r,{displaystyle {begin{Matrix}napprox {fnMicrosoft {1+cH00} ¿Qué? {fncHFF {cHFF}varepsilon ¿Qué?

donde ε_r es la permitividad relativa del medio.

Para la caracterización de los vidrios se suele utilizar la ecuación que consta de tres términos:

n2()λ λ )=1+B1λ λ 2λ λ 2− − C1+B2λ λ 2λ λ 2− − C2+B3λ λ 2λ λ 2− − C3,{displaystyle n^{2}(lambda)=1+{frac {B_{1}lambda ¿Qué? {B_{2}lambda ¿Qué? {B_{3}lambda ^{2}-C_{3}}}

Como ejemplo, a continuación se muestran los coeficientes para un vidrio corona de borosilicato común conocido como BK7:

Para los anteojos ópticos comunes, el índice de refracción calculado con la ecuación de Sellmeier de tres términos se desvía del índice de refracción real en menos de 5×10⁻⁶ en las longitudes de onda' rango de 365 nm a 2,3 μm, que es del orden de la homogeneidad de una muestra de vidrio. A veces se agregan términos adicionales para que el cálculo sea aún más preciso.

A veces, la ecuación de Sellmeier se usa en forma de dos términos:

n2()λ λ )=A+B1λ λ 2λ λ 2− − C1+B2λ λ 2λ λ 2− − C2.{displaystyle n^{2}(lambda)=A+{frac {B_{1}lambda ¿Qué? {B_{2}lambda ^{2}{lambda ^{2}-C_{2}}}

Aquí, el coeficiente A es una aproximación de las contribuciones de absorción de longitud de onda corta (por ejemplo, ultravioleta) al índice de refracción en longitudes de onda más largas. Existen otras variantes de la ecuación de Sellmeier que pueden explicar el cambio del índice de refracción de un material debido a la temperatura, la presión y otros parámetros.

Coeficientes