Ecuación de Sackur-Tetrodo

La ecuación de Sackur-Tetrode es una expresión para la entropía de un gas ideal monoatómico.

Lleva el nombre de Hugo Martin Tetrode (1895–1931) y Otto Sackur (1880–1914), quienes lo desarrollaron de forma independiente como una solución de las ecuaciones de entropía y estadísticas de gases de Boltzmann, aproximadamente al mismo tiempo en 1912. .

Fórmula

La ecuación de Sackur-Tetrode expresa la entropía ${\displaystyle S.$ de un gas ideal monoatámico en términos de su estado termodinámico—específicamente, su volumen ${\displaystyle V}$, energía interna ${\displaystyle U}$, y el número de partículas ${\displaystyle N}$:

${\displaystyle {\fnMicroc {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fn} {\fnMicrosoft}} {\fnMicrosoft}}} {\fnMicrosoft}} {\fnMicroc}} {\fnMicroc} {B}N}=\ln \left [{\frac {V}{N}\left({\frac {4\pi} {\fnh} {\fnh}} {\fnh}} {\fnh} {\fnh}}}} {\fn}}}}$

Donde ${\displaystyle k_{\mathrm {B}$ es la constante de Boltzmann, ${\displaystyle m}$ es la masa de una partícula de gas y ${\displaystyle h}$ es la constante Planck.

La ecuación también se puede expresar en términos de longitud de onda térmica ${\displaystyle \Lambda }$:

${\displaystyle {\fnMicroc {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fn} {\fnMicrosoft}} {\fnMicrosoft}}} {\fnMicrosoft}} {\fnMicroc}} {\fnMicroc} {B}N}=\ln \left({\frac [V] {N\Lambda ^{3}}\right)+{\frac {5}{2}}$

Para obtener una derivación de la ecuación de Sackur-Tetrode, consulte la paradoja de Gibbs. Para conocer las limitaciones impuestas a la entropía de un gas ideal únicamente por la termodinámica, consulte el artículo sobre gases ideales.

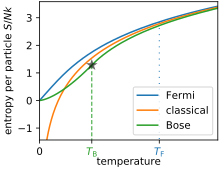
Las expresiones anteriores suponen que el gas está en el régimen clásico y está descrito por las estadísticas de Maxwell-Boltzmann (con el "conteo correcto de Boltzmann"). Según la definición de longitud de onda térmica, esto significa que la ecuación de Sackur-Tetrode es válida sólo cuando

${\displaystyle {\frac}{N\Lambda . 1.}$

La entropía predicha por la ecuación de Sackur-Tetrode se acerca al infinito negativo cuando la temperatura se acerca a cero.

Constante de Sackur-Tetrodo

La constante de Sackur-Tetrode, escrita S₀/R, es igual a S /k_BN evaluado a una temperatura de T = 1 kelvin, a presión estándar (100 kPa o 101,325 kPa, a especificarse), para un mol de un gas ideal compuesto por partículas de masa igual a la constante de masa atómica (m_u = 1.660539066 60(50)×10⁻²⁷ kg). Su valor recomendado CODATA 2018 es:

S₀/R = −1.15170753706(45) para p^o = 100 kPa

S₀/R = −1.16487052358(45) para p^o = 101.325 kPa.

Interpretación de la teoría de la información

Además de la perspectiva termodinámica de la entropía, las herramientas de la teoría de la información se pueden utilizar para proporcionar una perspectiva de la información de la entropía. En particular, es posible derivar la ecuación de Sackur-Tetrode en términos de teoría de la información. La entropía general se representa como la suma de cuatro entropías individuales, es decir, cuatro fuentes distintas de información faltante. Se trata de la incertidumbre posicional, la incertidumbre de los momentos, el principio de incertidumbre de la mecánica cuántica y la indistinguibilidad de las partículas. Sumando las cuatro piezas, la ecuación de Sackur-Tetrode queda como

${\displaystyle {\begin{aligned}{\frac} {S}{k_{\rm {B}N}} {\ln V]+\left[{\frac {3}{2}}\ln\left(2\pi emk_{\rm}}\ln\ln}}\ln\ln\left(2\pi emk_{\rm} {B}T\right)\right]+[-3\ln h]+\left[-{\frac {\ln N!}{N}}\right]\\\\bun\ln\left[{\frac\frac] {\fn}\fn}\fnh}\m}\m}\m}\m}\m} {\fn}\m} {\fn}\m} {\fn} {\fn\fn}\fn}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m\m\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\m}\ mk_{\rm {B}T}{h^{2}}}}} {\frac {3}{2}\right]+{\frac {5}{2}}\end{aligned}}}} {\f}}} {\fn}}}}} {\f}}} {\f} {\f}}}} {\f}}}}}}} {\f}}}}}}}}}}}}}}} {\f}}}}} {\f}}}}}}}}}}} {\f}}}}}}}} {\f}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\f}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}}}$

La derivación utiliza la aproximación de Stirling, ${\displaystyle \ln N!\approx N\ln N-N.$. Strictly speaking, the use of dimensioned arguments to the logarithms is incorrect, however their use is a "shortcut" made for breast. Si cada argumento logarítmico fuera dividido por un valor estándar no especificado expresado en términos de una masa estándar no especificada, longitud y tiempo, estos valores estándar cancelarían en el resultado final, dando la misma conclusión. Los términos de entropía individual no serán absolutos, sino que dependerán más bien de los estándares elegidos, y difieren con diferentes estándares por una constante aditiva.