Ecuación de Langevin

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Ecuación diferencial estocástica

En física, una ecuación langevin (llamada así por Paul Langevin) es una ecuación diferencial estocástica que describe cómo un sistema evoluciona cuando se somete a una combinación de determinista y fluctuante (" aleatorio ") fuerzas. Las variables dependientes en una ecuación de Langevin típicamente son variables colectivas (macroscópicas) que cambian lentamente en comparación con las otras variables (microscópicas) del sistema. Las variables rápidas (microscópicas) son responsables de la naturaleza estocástica de la ecuación de Langevin. Una aplicación es el movimiento browniano, que modela el movimiento fluctuante de una pequeña partícula en un fluido.

movimiento brownian como prototipo

La ecuación original de Langevin describe el movimiento browniano, el movimiento aparentemente aleatorio de una partícula en un fluido debido a colisiones con las moléculas del fluido,

{displaystyle m{frac {dmathbf {v} }{dt}}=-lambda mathbf {v} +{boldsymbol {eta }}left(tright).}

Aquí, $mathbf {v}$ es la velocidad de la partícula, $lambda$ es su coeficiente de amortiguación, y $m$ es su masa. La fuerza que actúa en la partícula está escrita como una suma de una fuerza viscosa proporcional a la velocidad de la partícula (Ley de los golpes), y un término de ruido ${displaystyle {boldsymbol {eta }}left(tright)}$ representando el efecto de las colisiones con las moléculas del fluido. La fuerza ${displaystyle {boldsymbol {eta }}left(tright)}$ tiene una distribución de probabilidad gaisiana con función de correlación

{displaystyle leftlangle eta _{i}left(tright)eta _{j}left(t'right)rightrangle =2lambda k_{text{B}}Tdelta _{i,j}delta left(t-t'right),}

k_{text{B}}

T

{displaystyle eta _{i}left(tright)}

{displaystyle {boldsymbol {eta }}left(tright)}

delta

- Función

t

delta

Otra característica común de la ecuación Langevin es la ocurrencia del coeficiente de amortiguación $lambda$ en la función de correlación de la fuerza al azar, que en un sistema de equilibrio es una expresión de la relación de Einstein.

aspectos matemáticos

A strictly $delta$ -fuerza fluctuante relacionada con la estructura ${displaystyle {boldsymbol {eta }}left(tright)}$ no es una función en el sentido matemático habitual e incluso el derivado ${displaystyle dmathbf {v} /dt}$ no se define en este límite. Este problema desaparece cuando la ecuación Langevin está escrita en forma integral ${textstyle mmathbf {v} =int ^{t}left(-lambda mathbf {v} +{boldsymbol {eta }}left(tright)right)dt.}$ Por lo tanto, la forma diferencial es sólo una abreviatura para su tiempo integral. El término matemático general para ecuaciones de este tipo es "ecuación diferencial estocástica".

Otra ambigüedad matemática ocurre para las ecuaciones de Langevin con ruido multiplicativo, que se refiere a términos de ruido que se multiplican por una función no constante de las variables dependientes, por ejemplo, ${displaystyle left|{boldsymbol {v}}(t)right|{boldsymbol {eta }}(t)}$ . Si un ruido multiplicativo es intrínseco para el sistema, su definición es ambiguo, ya que es igualmente válido interpretarlo de acuerdo con el esquema Stratonovich- o Ito- (ver cálculo Itō). Sin embargo, los observables físicos son independientes de la interpretación, siempre y cuando éste se aplique de forma sistemática al manipular la ecuación. Esto es necesario porque las reglas simbólicas del cálculo difieren dependiendo del esquema de interpretación. Si el ruido es externo al sistema, la interpretación adecuada es la Stratonovich.

Ecuación genérica de Langevin

Hay una derivación formal de una ecuación de Langevin genérica de la mecánica clásica. Esta ecuación genérica juega un papel central en la teoría de la dinámica crítica y otras áreas de la mecánica estadística de no equilibrio. La ecuación para el movimiento browniano anterior es un caso especial.

Un paso esencial en la derivación es la división de los grados de libertad en las categorías lento y rápido. Por ejemplo, el equilibrio termodinámico local en un líquido se alcanza en unos pocos tiempos de colisión, pero las densidades de cantidades conservadas, como la masa y la energía, tardan mucho más en relajarse hasta alcanzar el equilibrio. Por lo tanto, las densidades de cantidades conservadas, y en particular sus componentes de longitud de onda larga, son candidatos variables lentos. Esta división se puede expresar formalmente con el operador de proyección de Zwanzig. Sin embargo, la derivación no es completamente rigurosa desde la perspectiva de la física matemática porque se basa en suposiciones que carecen de pruebas rigurosas y, en cambio, se justifican solo como aproximaciones plausibles de sistemas físicos.

Vamos ${displaystyle A={A_{i}}}$ denota las variables lentas. La ecuación genérica de Langevin lee

{displaystyle {frac {dA_{i}}{dt}}=k_{text{B}}Tsum limits _{j}{left[{A_{i},A_{j}}right]{frac {{d}{mathcal {H}}}{dA_{j}}}}-sum limits _{j}{lambda _{i,j}left(Aright){frac {d{mathcal {H}}}{dA_{j}}}+}sum limits _{j}{frac {d{lambda _{i,j}left(Aright)}}{dA_{j}}}+eta _{i}left(tright).}

La fuerza fluctuante ${displaystyle eta _{i}left(tright)}$ obedece una distribución de probabilidad gausiana con función de correlación

{displaystyle leftlangle {eta _{i}left(tright)eta _{j}left(t'right)}rightrangle =2lambda _{i,j}left(Aright)delta left(t-t'right).}

Esto implica la relación de reciprocidad de Onsager ${displaystyle lambda _{i,j}=lambda _{j,i}}$ para los coeficientes de amortiguación $lambda$ . La dependencia ${displaystyle dlambda _{i,j}/dA_{j}}$ de $lambda$ on $A$ es insignificante en la mayoría de los casos. El símbolo ${displaystyle {mathcal {H}}=-ln left(p_{0}right)}$ denota al Hamiltoniano del sistema, donde ${displaystyle p_{0}left(Aright)}$ es la distribución de probabilidad de equilibrio de las variables $A$ . Finalmente, $[A_{i},A_{j}]$ es la proyección del soporte Poisson de las variables lentas $A_{i}$ y $A_{j}$ sobre el espacio de variables lentas.

En el caso de movimiento Brownian uno habría ${displaystyle {mathcal {H}}=mathbf {p} ^{2}/left(2mk_{text{B}}Tright)}$ , ${displaystyle A={mathbf {p} }}$ o ${displaystyle A={mathbf {x}mathbf {p} }}$ y ${displaystyle [x_{i},p_{j}]=delta _{i,j}}$ . La ecuación del movimiento ${displaystyle dmathbf {x} /dt=mathbf {p} /m}$ para $mathbf {x}$ es exacto: no hay fuerza fluctuante ${displaystyle eta _{x}}$ y sin coeficiente de amortiguación ${displaystyle lambda _{x,p}}$ .

Ejemplos

Ruido térmico en una resistencia eléctrica

Un circuito eléctrico compuesto por un resistor y un condensador.

Hay una analogía estrecha entre la partícula marroniana paradigmática discutida anteriormente y el ruido de Johnson, el voltaje eléctrico generado por las fluctuaciones térmicas en un resistor. El diagrama a la derecha muestra un circuito eléctrico que consiste en una resistencia R y una condensación C. La variable lenta es el voltaje U entre los extremos de la resistencia. El Hamiltonian lee ${displaystyle {mathcal {H}}=E/k_{text{B}}T=CU^{2}/(2k_{text{B}}T)}$ , y la ecuación Langevin se convierte

{displaystyle {frac {dU}{dt}}=-{frac {U}{RC}}+eta left(tright),;;leftlangle eta left(tright)eta left(t'right)rightrangle ={frac {2k_{text{B}}T}{RC^{2}}}delta left(t-t'right).}

Esta ecuación puede usarse para determinar la función de correlación

{displaystyle leftlangle Uleft(tright)Uleft(t'right)rightrangle ={frac {k_{text{B}}T}{C}}exp left(-{frac {left|t-t'right|}{RC}}right)approx 2Rk_{text{B}}Tdelta left(t-t'right),}

C

Dinámica crítica

La dinámica del parámetro de orden $varphi$ de una segunda fase de orden la transición se desacelera cerca del punto crítico y se puede describir con una ecuación Langevin. El caso más simple es la clase universal "model A" con un parámetro de orden escalar no conservado, realizado por ejemplo en ferromagnetes axiales,

{displaystyle {begin{aligned}{frac {partial varphi left(mathbf {x}tright)}{partial t}}&=-lambda {frac {delta {mathcal {H}}}{delta varphi }}+eta left(mathbf {x}tright),\{mathcal {H}}&=int d^{d}xleft[{frac {1}{2}}r_{0}varphi ^{2}+uvarphi ^{4}+{frac {1}{2}}(nabla varphi)^{2}right],\[2pt]leftlangle eta left(mathbf {x}tright)eta left(mathbf {x} ',t'right)rightrangle &=2lambda delta left(mathbf {x} -mathbf {x} 'right)delta left(t-t'right).end{aligned}}}

Oscilador armónico en un fluido

{displaystyle m{frac {dv}{dt}}=-lambda v+eta (t)-kx}

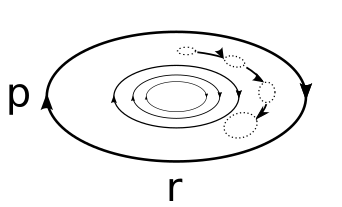
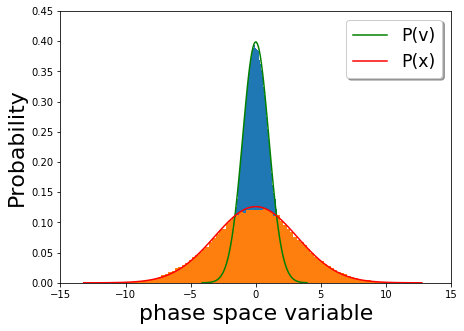
Una partícula en un fluido es descrita por una ecuación Langevin con una función energética potencial, una fuerza de amortiguación y fluctuaciones térmicas dadas por la disipación de fluctuación teorema. Si el potencial es cuadrático, las curvas de energía constantes son elipses, como se muestra en la figura. Si hay disipación pero no hay ruido térmico, una partícula pierde continuamente energía al medio ambiente, y su retrato de fase dependiente del tiempo (velocidad vs posición) corresponde a una espiral interior hacia 0 velocidad. Por el contrario, las fluctuaciones térmicas agregan continuamente energía a la partícula y evitan que alcance exactamente 0 velocidad. Más bien, el conjunto inicial de osciladores estocásticos se acerca a un estado estable en el que la velocidad y la posición se distribuyen de acuerdo con la distribución Maxwell-Boltzmann. En el diagrama abajo (figura 2), la distribución de velocidad de largo tiempo (orange) y distribuciones de posición (azul) en un potencial armónico ( ${textstyle U={frac {1}{2}}kx^{2}}$ ) está trazado con las probabilidades Boltzmann de velocidad (rojo) y posición (verde). En particular, el comportamiento tardío representa el equilibrio térmico.

Trayectorias de partículas brownianas libres

Considere una partícula libre de masa $m$ con ecuación de movimiento descrito por

{displaystyle m{frac {dmathbf {v} }{dt}}=-{frac {mathbf {v} }{mu }}+{boldsymbol {eta }}(t),}

{displaystyle mathbf {v} =dmathbf {r} /dt}

mu

{displaystyle {boldsymbol {eta }}(t)=mmathbf {a} (t)}

t_c

{displaystyle {overline {{boldsymbol {eta }}(t)}}=0}

{displaystyle mathbf {v} (t)=mathbf {v} (0)e^{-t/tau }+int _{0}^{t}mathbf {a} (t')e^{-(t-t')/tau }dt',}

{displaystyle tau =mmu }

mathbf {v}

Desplazamientos cuadrados simulados de partículas marrones libres (líneas semitransparentes) como función del tiempo, para tres opciones seleccionadas de velocidad cuadrada inicial que son 0, 3k_BT/m, y 6k_BT/m respectivamente, con 3k_BT/m siendo el valor equipartitivo en el equilibrio térmico. Las curvas sólidas de colores denotan los desplazamientos cuadrados medios para las opciones correspondientes del parámetro.

{displaystyle {begin{aligned}R_{vv}(t_{1},t_{2})&equiv langle mathbf {v} (t_{1})cdot mathbf {v} (t_{2})rangle \&=v^{2}(0)e^{-(t_{1}+t_{2})/tau }+int _{0}^{t_{1}}int _{0}^{t_{2}}R_{aa}(t_{1}',t_{2}')e^{-(t_{1}+t_{2}-t_{1}'-t_{2}')/tau }dt_{1}'dt_{2}'\&simeq v^{2}(0)e^{-|t_{2}-t_{1}|/tau }+left[{frac {3k_{text{B}}T}{m}}-v^{2}(0)right]{Big [}e^{-|t_{2}-t_{1}|/tau }-e^{-(t_{1}+t_{2})/tau }{Big ]},end{aligned}}}

{displaystyle mathbf {a} (t_{1}')}

{displaystyle mathbf {a} (t_{2}')}

{displaystyle t_{2}'-t_{1}'gg t_{c}}

{textstyle lim _{tto infty }langle v^{2}(t)rangle =lim _{tto infty }R_{vv}(t,t)}

{displaystyle 3k_{text{B}}T/m}

{displaystyle v^{2}(0)=3k_{text{B}}T/m}

{displaystyle langle v^{2}(t)rangle =3k_{text{B}}T/m}

t

La velocidad $mathbf {v} (t)$ de la partícula marroniana se puede integrar para producir su trayectoria ${mathbf {r}}(t)$ . Si se encuentra inicialmente en el origen con probabilidad 1, entonces el resultado es

{displaystyle mathbf {r} (t)=mathbf {v} (0)tau left(1-e^{-t/tau }right)+tau int _{0}^{t}mathbf {a} (t')left[1-e^{-(t-t')/tau }right]dt'.}

Por consiguiente, el desplazamiento medio ${textstyle langle mathbf {r} (t)rangle =mathbf {v} (0)tau left(1-e^{-t/tau }right)}$ asintotos a ${displaystyle mathbf {v} (0)tau }$ mientras el sistema se relaja. El desplazamiento cuadrado medio se puede determinar de forma similar:

{displaystyle langle r^{2}(t)rangle =v^{2}(0)tau ^{2}left(1-e^{-t/tau }right)^{2}-{frac {3k_{text{B}}T}{m}}tau ^{2}left(1-e^{-t/tau }right)left(3-e^{-t/tau }right)+{frac {6k_{text{B}}T}{m}}tau t.}

Esta expresión implica que ${displaystyle langle r^{2}(tll tau)rangle simeq v^{2}(0)t^{2}}$ , indicando que el movimiento de partículas marrones en tiempos mucho más cortos que el tiempo de relajación $tau$ del sistema es (aproximadamente) invariante reversal temporal. Por otro lado, ${displaystyle langle r^{2}(tgg tau)rangle simeq 6k_{text{B}}Ttau t/m=6mu k_{text{B}}Tt=6Dt}$ , lo que indica un proceso irreversible y disipante.

Esta parcela corresponde a soluciones de la ecuación Langevin completa obtenida utilizando el método Euler-Maruyama. El panel izquierdo muestra la evolución del tiempo del retrato de fase de un oscilador armónico a diferentes temperaturas. El panel derecho captura las distribuciones correspondientes de probabilidad de equilibrio. A temperatura cero, la velocidad se descompone rápidamente de su valor inicial (el punto rojo) a cero debido al amortiguamiento. Para temperaturas no ceros, la velocidad se puede patear a valores superiores al valor inicial debido a las fluctuaciones térmicas. A largo plazo, la velocidad sigue siendo no cero, y las distribuciones de posición y velocidad corresponden a la del equilibrio térmico.

Recuperación de las estadísticas de Boltzmann

Si el potencial externo es conservador y el término de ruido deriva de un embalse en equilibrio térmico, entonces la solución a largo plazo a la ecuación Langevin debe reducir a la distribución Boltzmann, que es la función de distribución de probabilidad para partículas en equilibrio térmico. En el caso especial de dinámicas sobredimensionadas, la inercia de la partícula es insignificante en comparación con la fuerza de amortiguación, y la trayectoria $x(t)$ es descrito por la ecuación de Langevin overdamped

{displaystyle lambda {frac {dx}{dt}}=-{frac {partial V(x)}{partial x}}+eta (t)equiv -{frac {partial V(x)}{partial x}}+{sqrt {2lambda k_{text{B}}T}}{frac {dB_{t}}{dt}},}

Donde $lambda$ es la constante de amortiguación. El término $eta (t)$ es el ruido blanco, caracterizado por ${displaystyle leftlangle eta (t)eta (t')rightrangle =2k_{text{B}}Tlambda delta (t-t')}$ (anteriormente, el proceso de Wiener). Una manera de resolver esta ecuación es introducir una función de prueba $f$ y calcula su promedio. El promedio de ${displaystyle f(x(t))}$ debe ser tiempo-independiente para finito $x(t)$ , conduce a

{displaystyle {frac {d}{dt}}leftlangle f(x(t))rightrangle =0,}

Es lema para el proceso de diffusión de deriva Itô ${displaystyle dX_{t}=mu _{t},dt+sigma _{t},dB_{t}}$ dice que el diferencial de una función dos veces diferente $f () t, x)$ es dado por

{displaystyle df=left({frac {partial f}{partial t}}+mu _{t}{frac {partial f}{partial x}}+{frac {sigma _{t}^{2}}{2}}{frac {partial ^{2}f}{partial x^{2}}}right)dt+sigma _{t}{frac {partial f}{partial x}},dB_{t}.}

Aplicar esto al cálculo de ${displaystyle langle f(x(t))rangle }$ da

{displaystyle leftlangle -f'(x){frac {partial V}{partial x}}+k_{text{B}}Tf''(x)rightrangle =0.}

Este promedio se puede escribir usando la función de densidad de probabilidad $p(x)$ ;

{displaystyle int left(-f'(x){frac {partial V}{partial x}}p(x)+{k_{text{B}}T}f''(x)p(x)right)dx=int left(-f'(x){frac {partial V}{partial x}}p(x)-{k_{text{B}}T}f'(x)p'(x)right)dx=0,}

f

{displaystyle {frac {partial V}{partial x}}p(x)+{k_{text{B}}T}p'(x)=0,}

{displaystyle p(x)propto exp left({-{frac {V(x)}{k_{text{B}}T}}}right).}

Técnicas equivalentes

En algunas situaciones, uno está principalmente interesado en el comportamiento promediado del ruido de la ecuación de Langevin, a diferencia de la solución para realizaciones particulares del ruido. Esta sección describe técnicas para obtener este comportamiento promediado que son distintas, pero también equivalentes, al cálculo estocástico inherente a la ecuación de Langevin.

Ecuación de Fokker-Planck

Una ecuación Fokker-Planck es una ecuación determinista para la densidad de probabilidad dependiente del tiempo ${displaystyle Pleft(A,tright)}$ de variables estocásticas $A$ . La ecuación Fokker-Planck correspondiente a la ecuación genérica Langevin descrita en este artículo es la siguiente:

{displaystyle {frac {partial Pleft(A,tright)}{partial t}}=sum _{i,j}{frac {partial }{partial A_{i}}}left(-k_{text{B}}Tleft[A_{i},A_{j}right]{frac {partial {mathcal {H}}}{partial A_{j}}}+lambda _{i,j}{frac {partial {mathcal {H}}}{partial A_{j}}}+lambda _{i,j}{frac {partial }{partial A_{j}}}right)Pleft(A,tright).}

{displaystyle P(A)=p_{0}(A)={text{const}}times exp(-{mathcal {H}})}

Ecuación de Klein-Kramers

La ecuación de Fokker-Planck para una partícula browniana subamortiguada se denomina ecuación de Klein-Kramers. Si las ecuaciones de Langevin se escriben como

{displaystyle {begin{aligned}{dot {mathbf {r} }}&={frac {mathbf {p} }{m}}\{dot {mathbf {p} }}&=-xi ,mathbf {p} -nabla V(mathbf {r})+{sqrt {2mxi k_{mathrm {B} }T}}{boldsymbol {eta }}(t),qquad langle {boldsymbol {eta }}^{mathrm {T} }(t){boldsymbol {eta }}(t')rangle =mathbf {I} delta (t-t')end{aligned}}}

mathbf {p}

{displaystyle {frac {partial f}{partial t}}+{frac {1}{m}}mathbf {p} cdot nabla _{mathbf {r} }f=xi nabla _{mathbf {p} }cdot left(mathbf {p} ,fright)+nabla _{mathbf {p} }cdot left(nabla V(mathbf {r}),fright)+mxi k_{mathrm {B} }T,nabla _{mathbf {p} }^{2}f}

{displaystyle nabla _{mathbf {r} }}

{displaystyle nabla _{mathbf {p} }}

r

p

{displaystyle nabla _{mathbf {p} }^{2}}

p

In $d$ -espacio libre dimensional, correspondiente a ${displaystyle V(mathbf {r})={text{constant}}}$ on ${mathbb {R}}^{{d}}$ , esta ecuación se puede resolver utilizando Fourier transforma. Si la partícula es inicializada $t=0$ con posición $mathbf {r} '$ e impulso ${displaystyle mathbf {p} '}$ , correspondiente a la condición inicial ${displaystyle f(mathbf {r}mathbf {p}0)=delta (mathbf {r} -mathbf {r} ')delta (mathbf {p} -mathbf {p} ')}$ , entonces la solución es

{displaystyle {begin{aligned}f(mathbf {r}mathbf {p}t)={frac {1}{left(2pi sigma _{X}sigma _{P}{sqrt {1-beta ^{2}}}right)^{d}}}exp left[-{frac {1}{2(1-beta ^{2})}}left({frac {|mathbf {r} -{boldsymbol {mu }}_{X}|^{2}}{sigma _{X}^{2}}}+{frac {|mathbf {p} -{boldsymbol {mu }}_{P}|^{2}}{sigma _{P}^{2}}}-{frac {2beta (mathbf {r} -{boldsymbol {mu }}_{X})cdot (mathbf {p} -{boldsymbol {mu }}_{P})}{sigma _{X}sigma _{P}}}right)right]end{aligned}}}

{displaystyle {begin{aligned}&sigma _{X}^{2}={frac {k_{mathrm {B} }T}{mxi ^{2}}}left[1+2xi t-left(2-e^{-xi t}right)^{2}right];qquad sigma _{P}^{2}=mk_{mathrm {B} }Tleft(1-e^{-2xi t}right)\&beta ={frac {k_{text{B}}T}{xi sigma _{X}sigma _{P}}}left(1-e^{-xi t}right)^{2}\&{boldsymbol {mu }}_{X}=mathbf {r} '+(mxi)^{-1}left(1-e^{-xi t}right)mathbf {p} ';qquad {boldsymbol {mu }}_{P}=mathbf {p} 'e^{-xi t}.end{aligned}}}

{displaystyle langle mathbf {r} (t)^{2}rangle =int f(mathbf {r}mathbf {p}t)mathbf {r} ^{2},dmathbf {r} dmathbf {p} ={boldsymbol {mu }}_{X}^{2}+3sigma _{X}^{2}}

Integral de trayectoria

Un camino integral equivalente a una ecuación Langevin se puede obtener de la ecuación correspondiente Fokker-Planck o mediante la transformación de la distribución de probabilidad gausiana ${displaystyle P^{(eta)}(eta)deta }$ de la fuerza fluctuante $eta$ a una distribución de probabilidad de las variables lentas, esquemáticamente ${displaystyle P(A)dA=P^{(eta)}(eta (A))det(deta /dA)dA}$ . Los determinantes funcionales y las sutilezas matemáticas asociadas abandonan si la ecuación Langevin se discretiza de la manera natural (causal), donde ${displaystyle A(t+Delta t)-A(t)}$ depende de $A(t)$ pero no ${displaystyle A(t+Delta t)}$ . Resulta conveniente introducir auxiliar variables de respuesta ${tilde {A}}$ . El camino integral equivalente a la ecuación genérica de Langevin luego lee

{displaystyle int P(A,{tilde {A}}),dA,d{tilde {A}}=Nint exp left(L(A,{tilde {A}})right)dA,d{tilde {A}},}

N

{displaystyle L(A,{tilde {A}})=int sum _{i,j}left{{tilde {A}}_{i}lambda _{i,j}{tilde {A}}_{j}-{widetilde {A}}_{i}left{delta _{i,j}{frac {dA_{j}}{dt}}-k_{text{B}}Tleft[A_{i},A_{j}right]{frac {d{mathcal {H}}}{dA_{j}}}+lambda _{i,j}{frac {d{mathcal {H}}}{dA_{j}}}-{frac {dlambda _{i,j}}{dA_{j}}}right}right}dt.}

Contenido relacionado

Más resultados...