Ecuación de la colina (bioquímica)

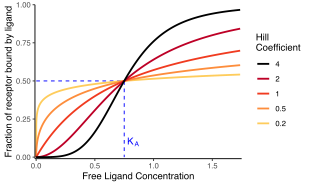
En bioquímica y farmacología, la ecuación de Hill se refiere a dos ecuaciones estrechamente relacionadas que reflejan la unión de ligandos a macromoléculas, en función de la concentración del ligando. Un ligando es "una sustancia que forma un complejo con una biomolécula para cumplir un propósito biológico"; (definición de ligando), y una macromolécula es una molécula muy grande, como una proteína, con una estructura compleja de componentes (definición de macromolécula). La unión proteína-ligando normalmente cambia la estructura de la proteína objetivo, cambiando así su función en una célula.

La distinción entre las dos ecuaciones de Hill es si miden la ocupación o la respuesta. La ecuación de Hill refleja la ocupación de macromoléculas: la fracción que está saturada o unida por el ligando. Esta ecuación es formalmente equivalente a la isoterma de Langmuir. Por el contrario, la ecuación de Hill propiamente dicha refleja la respuesta celular o tisular al ligando: la salida fisiológica del sistema, como la contracción muscular.

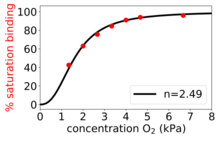
La ecuación de Hill fue formulada originalmente por Archibald Hill en 1910 para describir la curva sigmoidea de unión de O₂ de la hemoglobina.

La unión de un ligando a una macromolécula a menudo mejora si ya hay otros ligandos presentes en la misma macromolécula (esto se conoce como unión cooperativa). La ecuación de Hill es útil para determinar el grado de cooperatividad del ligando que se une a la enzima o al receptor. El coeficiente de Hill proporciona una forma de cuantificar el grado de interacción entre los sitios de unión del ligando.

La ecuación de Hill (para la respuesta) es importante en la construcción de curvas dosis-respuesta.

Proporción de receptores ligand-bound

La ecuación de Hill se expresa comúnmente de las siguientes maneras.

Silencio Silencio =[L]nKd+[L]n=[L]n()KA)n+[L]n=11+()KA[L])n{displaystyle {begin{aligned}theta {fn} {fn}}\fn}\fn}\\fn}\\n}\\c}\\c}\c}\\c}\\c}\\c}\\c}\\cH3}\c}\\\c}}\\c}}}\\\\c}}}\\\c}}}}}\\\\c}}}\\\\\\c}}}}\\\c}}}\\\c}}}\\c}}}}\\\\\\\\\c}}}}}}}}\\c}}}}\\\c}}\\\\c}}} {fn} {fn}\fn}\fn}n}\cn}\\cn}\cn}\cn}n}n}n}n}n}n}n}n}}end{aligned}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {n}}} {n}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {,

donde:

• Silencio Silencio {displaystyle theta } es la fracción de la concentración de proteína receptora que está ligada por el ligando,
• [L]{displaystyle {ce {}}}}es la concentración total de ligando,
• Kd{displaystyle K_{d} es la aparente constante de disociación derivada de la ley de acción masiva,
• KA{displaystyle K_{A}es la concentración de ligando que produce la mitad de ocupación,
• n{displaystyle n} es el coeficiente Hill.

El caso especial donde n=1{displaystyle n=1} es una ecuación Monod.

constantes

En farmacología, Silencio Silencio {displaystyle theta } a menudo escrito como pAR{displaystyle {fnK}}, donde A{displaystyle {ce {}}} es el ligando, equivalente a L, y R{displaystyle {ce {}}} es el receptor. Silencio Silencio {displaystyle theta } se puede expresar en términos de la cantidad total de concentraciones de receptores y receptores de ligando: Silencio Silencio =[LR][Rtotal]{displaystyle theta ={frac {ce {c}{ce {c}}}}}}}}}}}}}}}. Kd{displaystyle K_{d} es igual a la relación de la tasa de disociación del complejo de receptores de ligand con su tasa de asociación (Kd=kdka{textstyle K_{rm {d}={k_{rm} {d} over k_{rm {a}}}). Kd es la constante de equilibrio para la disociación. KA{textstyle K_{A}} se define de modo que ()KA)n=Kd=kdka{textstyle (K_{A}=K_{rm} {d}={k_{rm} {d} over k_{rm {a}}}, esto también se conoce como la constante de disociación microscópica y es la concentración de ligando que ocupa la mitad de los sitios de unión. En la literatura reciente, esta constante a veces se conoce como KD{textstyle K_{D}.

Ecuación de Gaddum

La ecuación Gaddum es una generalización adicional de la ecuación de la colina, que incorpora la presencia de un antagonista competitivo reversible. La ecuación de Gaddum se deriva de manera similar a la ecuación de la colina pero con 2 equilibrios: tanto el ligando con el receptor como el antagonista con el receptor. Por lo tanto, la ecuación de Gaddum tiene 2 constantes: las constantes de equilibrio del ligando y las del antagonista

Hill Plot

El diagrama de Hill es la reordenación de la ecuación de Hill en una línea recta.

Tomar el recíproco de ambos lados de la ecuación de Hill, reorganización e invertir de nuevo rendimientos: Silencio Silencio 1− − Silencio Silencio =[L]nKd=[L]n()KA)n{displaystyle {theta over 1-theta }={ { {ce {fn} {fn} {fn} {fn} {fn}} {fn}} {fn}}} {fn} {fn}} {fn}}}}}} {c}}}} {c}}} {cH}}}}}}}}}}} {c}}}}}}}}}}}}}}}}} {c}} {c}}}}}}} {c} {c}}}}}} {c}}}}}}}}}}} {c}}}}}}}}} {c}}}}}} {c}}}}}} {c}}}}} {c}}}}}}}}}}}} {c}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}} { {fn}. Tomar el logaritmo de ambos lados de la ecuación conduce a una formulación alternativa de la ecuación Hill-Langmuir:

log⁡ ⁡ ()Silencio Silencio 1− − Silencio Silencio )=nlog⁡ ⁡ [L]− − log⁡ ⁡ Kd=nlog⁡ ⁡ [L]− − nlog⁡ ⁡ KA{displaystyle {begin{aligned}log left({theta over 1-theta ################################################################################################################################################################################################################################################################ {K_{d}\\\\fnfn} {fn} {fn} {fn} {fn}} {fn}}} {fn} {fn}} {fn}}}} {fn}}} {fn} {fn}}}}}} {fnfnf}}} {fnfnf}}} {f}}}}} {f}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

Esta última forma de la ecuación Hill es ventajosa porque una parcela log⁡ ⁡ ()Silencio Silencio 1− − Silencio Silencio ){textstyle log left({theta over 1-theta }right)} versus log⁡ ⁡ [L]{displaystylelog {}}}} produce una trama lineal, que se llama Hill plot. Debido a que la pendiente de una parcela Hill es igual al coeficiente Hill para la interacción bioquímica, la pendiente se denota por nH{displaystyle No.. Una pendiente mayor a una indica por lo tanto la unión positiva de cooperación entre el receptor y el ligand, mientras que una pendiente inferior a una indica la unión de cooperación negativa.

Las transformaciones de ecuaciones en formas lineales como esta eran muy útiles antes del uso generalizado de las computadoras, ya que permitían a los investigadores determinar parámetros ajustando líneas a los datos. Sin embargo, estas transformaciones afectan la propagación del error y esto puede dar como resultado una ponderación indebida del error en puntos de datos cercanos a 0 o 1. Esto afecta los parámetros de las líneas de regresión lineal ajustadas a los datos. Además, el uso de computadoras permite un análisis más sólido que involucra regresión no lineal.

Respuesta del tejido

Debe hacerse una distinción entre la cuantificación de los fármacos vinculantes para los receptores y los medicamentos que producen respuestas. Puede que no haya necesariamente una relación lineal entre los dos valores. En contraste con la definición anterior de este artículo de la ecuación Hill, el IUPHAR define la ecuación Hill en términos de la respuesta del tejido ()E){displaystyle (E)}, como

EEmax=[A]nCE50n+[A]n=11+()CE50[A])n{displaystyle {begin{aligned}{frac} {fn} {fn} {fn}}} {fn}} {fn} {fn} {fn}} {fn}}} {fn}}}}\fn}\\fn}\\fn}\\fn}\\fn}}\\\\\\fn}\\\fn}\\\fn}\\\fn}\fn}}\\\\\\\\\fn}\\\\fn}\\\\\fn}\\fn}\\fn}\\fn}\fn}\\fn}\\\fn}fn}\\\\\\\\\\fn {1}{1+left {frac {text{EC}}{50}{}}right)} {n}}end{aligned}}}}}}} {fn}}} {fn}}}} {fn}}}} {fn} {f}}}}} {fnf}}}}}}}}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

[A]{displaystyle {ce {}}}

n{displaystyle n}

CE50{displaystyle {text{EC}_{50}}

CE50{displaystyle {text{EC}_{50}}

Esta forma de la ecuación puede reflejar las respuestas de tejido/celular/población a los medicamentos y puede utilizarse para generar curvas de respuesta a dosis. La relación entre Kd{displaystyle K_{d} y EC50 puede ser bastante complejo ya que una respuesta biológica será la suma de los factores de miríada; un fármaco tendrá un efecto biológico diferente si hay más receptores presentes, independientemente de su afinidad.

El modelo de Del-Castillo Katz se utiliza para relacionar la ecuación de Hill con la activación del receptor al incluir un segundo equilibrio del receptor unido al ligando con una forma activada del receptor unido al ligando.

El análisis estadístico de la respuesta en función del estímulo se puede realizar mediante métodos de regresión como el modelo probit o el modelo logit, u otros métodos como el método de Spearman-Kärber. Generalmente se prefieren los modelos empíricos basados en regresión no lineal al uso de alguna transformación de los datos que linealice la relación dosis-respuesta.

Coeficiente de colina

El coeficiente de Hill es una medida de ultrasensibilidad (es decir, qué tan pronunciada es la curva de respuesta).

El coeficiente Hill, n{displaystyle n} o nH{displaystyle No., puede describir la cooperación (o posiblemente otras propiedades bioquímicas, dependiendo del contexto en el que se utilice la ecuación Hill). Cuando sea apropiado, el valor del coeficiente Hill describe la cooperación de ligand vinculante de la siguiente manera:

• 1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>. Cooperación positiva: Una vez que una molécula de ligando está ligada a la enzima, su afinidad para otras moléculas de ligando aumenta. Por ejemplo, el coeficiente Hill de oxigeno ligado a la hemoglobina (un ejemplo de cooperación positiva) cae dentro del rango de 1.7-3.2.
• <math alttext="{displaystyle nnc)1{displaystyle n made1}<img alt="{displaystyle n. Cooperativamente vinculante: Una vez que una molécula de ligando está ligada a la enzima, su afinidad para otras moléculas de ligando disminuye.
• n=1{displaystyle n=1}. Noncooperative (completamente independiente) binding: La afinidad de la enzima para una molécula de ligando no depende de si otras moléculas de ligando ya están ligadas. Cuando n=1, obtenemos un modelo que puede ser modelado por Michaelis-Menten kinetics, en el cual KD=KA=KM{fnMicrosoftstyle K_{D}=K_{A}=K_{M}, la constante de Michaelis-Menten.

El coeficiente de la colina se puede calcular aproximadamente en términos del índice de cooperatividad de Taketa y Pogell como sigue:

n=log10⁡ ⁡ ()81)log10⁡ ⁡ ()CE90/CE10){displaystyle n={frac {log _{10}(81)}{log _{10}({ce} {EC90}/{ce {}}}}} {}}} {}}}} {}} {}}} {}}} {}}}} {}}}} {}}}}}} {}}} {}}} {}}}}} {}}}} {}}}}} {}}}}}} {}}}}}} {}}}}} {}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

Donde CE90{displaystyle {ce {}}} y CE10{displaystyle {ce {}}} son los valores de entrada necesarios para producir el 10% y el 90% de la respuesta máxima, respectivamente.

Forma reversible

La forma más común de la ecuación de Hill es su forma irreversible. Sin embargo, cuando se construyen modelos computacionales, a menudo se requiere una forma reversible para modelar la inhibición del producto. Por esta razón, Hofmeyr y Cornish-Bowden idearon la ecuación reversible de Hill.

Relación con los coeficientes de elasticidad

El coeficiente de Hill también está íntimamente relacionado con el coeficiente de elasticidad, donde se puede demostrar que el coeficiente de Hill es igual a:

n=ε ε sv11− − Silencio Silencio {displaystyle n=varepsilon _{v}{v}{frac {1}{1-theta }

Donde Silencio Silencio {displaystyle theta } es la saturación fraccional, ES/Et{displaystyle ES/E_{t}, y ε ε sv{displaystyle varepsilon _{v}} el coeficiente de elasticidad.

Esto se obtiene tomando la pendiente de la ecuación de Hill:

n=dlog⁡ ⁡ Silencio Silencio 1− − Silencio Silencio dlog⁡ ⁡ s{fnMicroc {fnMicroc} {theta }{1-theta } {dlog s}

y la ampliación de la pendiente utilizando la regla del cociente. El resultado muestra que la elasticidad nunca puede exceder n{displaystyle n} ya que la ecuación anterior se puede reorganizar a:

ε ε sv=n()1− − Silencio Silencio ){displaystyle varepsilon _{v}=n(1-theta)}

Aplicaciones

La ecuación de Hill se utiliza ampliamente en farmacología para cuantificar los parámetros funcionales de un fármaco y también se utiliza en otras áreas de la bioquímica.

La ecuación de Hill se puede utilizar para describir las relaciones dosis-respuesta, por ejemplo, la probabilidad de apertura del canal iónico (P-open) frente a la concentración del ligando.

Regulación de la transcripción genética

La ecuación de Hill se puede aplicar para modelar la velocidad a la que se produce un producto genético cuando su gen original está regulado por factores de transcripción (p. ej., activadores y/o represores). Hacerlo es apropiado cuando un gen está regulado por múltiples sitios de unión para factores de transcripción, en cuyo caso los factores de transcripción pueden unirse al ADN de manera cooperativa.

Si la producción de proteína del gen X está regulada positivamente (activada) por un factor de transcripción Y, luego la tasa de producción de proteína X se puede modelar como una ecuación diferencial en términos de la concentración de proteína Y activada:

ddt[Xproduced]=k ⋅ ⋅ [Yactive]n()KA)n + [Yactive]n{displaystyle {mathrm} over mathrm {d} t} [{rm {X_{produced}}=k {cdot {{rm {fn}}} {m}} {fn}} {fn} {fn} {fn}}}cdot {cdot {fn} {fn} {fn}} {fn}}cdot {cdot} {cdot {cdot}}}}} {cdot {cdot {cdot {cdot {cdot}}}}}}} {cdot {cdot {cdot} {cdot {\\\\\\\cdot}}}}}}} {cdot}}} {cdot}}}}}}}}}}} {cdot {cdot} {\cdot}}}}}}}}}cdot} {\cdot}}}}}}}}}}}}} + {fnh}} {fnh}} {fnh}}} {fn}}}}} {fn}}} {\fn}}}}} {\\\\\\\\\\\\\\\\\fnh}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}},

donde k es la tasa de transcripción máxima del gen X.

Del mismo modo, si la producción de proteínas del gen Y está regulada negativamente (reprimida) por un factor de transcripción Z, entonces la tasa de producción de proteína Y se puede modelar como una ecuación diferencial en términos de la concentración de proteína Z activada:

ddt[Yproduced]=k ⋅ ⋅ ()KA)n()KA)n + [Zactive]n{displaystyle {mathrm} over mathrm {d} t} [{rm {Y_{produced}}=k {cdot { {fn} {fn}} {fn}}cdot { {fn} {fn}} {n}}n}cdot {cdot {cdot} {fn}} {cdot {cdot {cdot}} {cdot {cdot}}}} {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot}}}}} {cdot {cdot {cdot {cdot {}}}}}}}}}}}}}}}}}}}}}}} {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {}}}}}}} + {fnh} {fnh}} {fnh}}} {fnh}}}}} {fn}}} {\fnh}}}}}}}}}} {\\\fnh}}}}}}}}}}} {\\cH}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\,

donde k es la tasa de transcripción máxima del gen Y.

Limitaciones

Debido a su suposición de que las moléculas de ligando se unen a un receptor simultáneamente, la ecuación de Hill ha sido criticada como un modelo físicamente poco realista. Además, el coeficiente de Hill no debe considerarse una aproximación confiable del número de sitios de unión de ligando cooperativo en un receptor, excepto cuando la unión del primer ligando y de los siguientes da como resultado una cooperatividad extremadamente positiva.

A diferencia de los modelos más complejos, la ecuación de Hill relativamente simple proporciona poca información sobre los mecanismos fisiológicos subyacentes de las interacciones proteína-ligando. Sin embargo, esta simplicidad es lo que hace que la ecuación de Hill sea un modelo empírico útil, ya que su uso requiere poco conocimiento a priori sobre las propiedades de la proteína o del ligando que se está estudiando. Sin embargo, se han propuesto otros modelos más complejos de vinculación cooperativa. Para obtener más información y ejemplos de dichos modelos, consulte Enlace cooperativo.

Las medidas de sensibilidad global como el coeficiente de Hill no caracterizan los comportamientos locales de las curvas en forma de s. En cambio, estas características quedan bien captadas por la medida del coeficiente de respuesta.

Existe un vínculo entre el coeficiente de Hill y el coeficiente de respuesta, como se muestra a continuación. Altszyler et al. (2017) han demostrado que estas medidas de ultrasensibilidad pueden vincularse.