Ecuación de Debye-Hückel

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Ecuación electroquímica

Los químicos Peter Debye y Erich Hückel notaron que las soluciones que contienen solutos iónicos no se comportan idealmente incluso en concentraciones muy bajas. Por lo tanto, si bien la concentración de los solutos es fundamental para el cálculo de la dinámica de una solución, teorizaron que un factor adicional que denominaron gamma es necesario para el cálculo de las actividades de la solución. De ahí que desarrollaron Debye-Hückel ecuación y Debye-Hückel limiting law. La actividad es sólo proporcional a la concentración y se altera por un factor conocido como coeficiente de actividad ${displaystyle gamma }$ . Este factor tiene en cuenta la energía de interacción de iones en solución.

Ley limitante de Debye-Hückel

Para calcular la actividad ${displaystyle a_{C}}$ de un ion C en una solución, se debe conocer la concentración y el coeficiente de actividad:

{displaystyle a_{C}=gamma {frac {mathrm {[C]} }{mathrm {[C^{ominus }]} }},}

${displaystyle gamma }$ es el coeficiente de actividad de C,
${displaystyle mathrm {[C^{ominus }]} }$ es la concentración de los elegidos Estado estándar, por ejemplo 1 ml/kg si se utiliza la molidad,
${displaystyle mathrm {[C]} }$ es una medida de la concentración de C.

Dividir ${displaystyle mathrm {[C]} }$ con ${displaystyle mathrm {[C^{ominus }]} }$ da una cantidad sin dimensión.

La ley limitante de Debye-Hückel permite determinar el coeficiente de actividad de un ion en una solución diluida de fuerza iónica conocida. La ecuación es

{displaystyle ln(gamma _{i})=-{frac {z_{i}^{2}q^{2}kappa }{8pi varepsilon _{r}varepsilon _{0}k_{text{B}}T}}=-{frac {z_{i}^{2}q^{3}N_{text{A}}^{1/2}}{4pi (varepsilon _{r}varepsilon _{0}k_{text{B}}T)^{3/2}}}{sqrt {10^{3}{frac {I}{2}}}}=-Az_{i}^{2}{sqrt {I}},}

${displaystyle z_{i}}$ es el número de carga de especies de iones i,
${displaystyle q}$ es la carga primaria,
${displaystyle kappa }$ es la inversa de la longitud de proyección de Debye ${displaystyle lambda _{rm {D}}}$ (definido a continuación),
${displaystyle varepsilon _{r}}$ es la relativa autorización del solvente,
${displaystyle varepsilon _{0}}$ es la autorización del espacio libre,
${displaystyle k_{text{B}}}$ es la constante de Boltzmann,
${displaystyle T}$ es la temperatura de la solución,
${displaystyle N_{mathrm {A} }}$ es la constante Avogadro,
${displaystyle I}$ es la fuerza iónica de la solución (definida a continuación),
${displaystyle A}$ es una constante que depende de la temperatura. Si ${displaystyle I}$ se expresa en términos de molidad, en lugar de molaridad (como en la ecuación anterior y en el resto de este artículo), entonces un valor experimental para ${displaystyle A}$ de agua es ${displaystyle 1.172{text{ mol}}^{-1/2}{text{kg}}^{1/2}}$ a 25 °C. Es común utilizar un logaritmo base-10, en cuyo caso factor ${displaystyle ln 10}$ , entonces A es ${displaystyle 0.509{text{ mol}}^{-1/2}{text{kg}}^{1/2}}$ . El multiplicador ${displaystyle 10^{3}}$ antes ${displaystyle I/2}$ en la ecuación es para el caso cuando las dimensiones ${displaystyle I}$ son ${displaystyle {text{mol}}/{text{dm}}^{3}}$ . Cuando las dimensiones ${displaystyle I}$ son ${displaystyle {text{mole}}/{text{m}}^{3}}$ , el multiplicador ${displaystyle 10^{3}}$ debe ser retirado de la ecuación.

Es importante tener en cuenta que debido a que los iones en la solución actúan juntos, el coeficiente de actividad obtenido de esta ecuación es en realidad un coeficiente de actividad medio.

El exceso de presión osmótica obtenido de la teoría de Debye-Hückel está en unidades cgs:

{displaystyle P^{text{ex}}=-{frac {k_{text{B}}Tkappa _{text{cgs}}^{3}}{24pi }}=-{frac {k_{text{B}}Tleft({frac {4pi sum _{j}c_{j}q_{j}}{varepsilon _{0}varepsilon _{r}k_{text{B}}T}}right)^{3/2}}{24pi }}.}

{textstyle P^{text{id}}=k_{text{B}}Tsum _{i}c_{i}}

{displaystyle phi ={frac {P^{text{id}}+P^{text{ex}}}{P^{text{id}}}}=1+{frac {P^{text{ex}}}{P^{text{id}}}}.}

Resumen del primer artículo de Debye y Hückel sobre la teoría de los electrolitos diluidos

El título en inglés del artículo es "Sobre la teoría de los electrolitos". I. Depresión del punto de congelación y fenómenos relacionados". Se publicó originalmente en 1923 en el volumen 24 de una revista en alemán Physikalische Zeitschrift. Se incluye una traducción al inglés del artículo en un libro de artículos recopilados presentado a Debye por "sus alumnos, amigos y editores con motivo de su septuagésimo cumpleaños el 24 de marzo de 1954". En 2019 se completó otra traducción al inglés. El artículo trata sobre el cálculo de las propiedades de soluciones de electrolitos que están bajo la influencia de campos eléctricos inducidos por iones, por lo que trata de la electrostática.

En el mismo año en que publicaron este artículo por primera vez, Debye y Hückel, en adelante D&H, también publicaron un artículo que cubría su caracterización inicial de soluciones bajo la influencia de campos eléctricos llamado "Sobre la teoría de los electrolitos". II. Ley Limitante de la Conductividad Eléctrica", pero el artículo siguiente no se trata (todavía) aquí.

En el siguiente resumen (aún incompleto y sin verificar), se utilizan notación y terminología modernas, tanto de química como de matemáticas, para evitar confusiones. Además, con algunas excepciones para mejorar la claridad, las subsecciones de este resumen son versiones (muy) condensadas de las mismas subsecciones del artículo original.

Introducción

D&H señala que la fórmula de Guldberg-Waage para especies de electrolitos en equilibrio de reacción química en forma clásica es

{displaystyle prod _{i=1}^{s}x_{i}^{nu _{i}}=K,}

${textstyle prod }$ es una notación para la multiplicación,
${displaystyle i}$ es una variable muñeca que indica la especie,
${displaystyle s}$ es el número de especies que participan en la reacción,
${displaystyle x_{i}}$ es la fracción del topo de las especies ${displaystyle i}$ ,
${displaystyle nu _{i}}$ es el coeficiente estoichiométrico de las especies ${displaystyle i}$ ,
K es la constante del equilibrio.

D.H dice que, debido a las "fuerzas electrostáticas recíprocas entre los iones", es necesario modificar la ecuación de Guldberg-Waage reemplazando ${displaystyle K}$ con ${displaystyle gamma K}$ , donde ${displaystyle gamma }$ es un coeficiente de actividad general, no un coeficiente de actividad "especial" (coeficiente de actividad independiente asociado a cada especie)—lo que se utiliza en la química moderna a partir de 2007.

La relación entre ${displaystyle gamma }$ y los coeficientes de actividad especiales ${displaystyle gamma _{i}}$ es

{displaystyle log(gamma)=sum _{i=1}^{s}nu _{i}log(gamma _{i}).}

Fundamentos

D comprimidoH usan las entropías libres Helmholtz y Gibbs ${displaystyle Phi }$ y ${displaystyle Xi }$ para expresar el efecto de las fuerzas electrostáticas en un electrolito en su estado termodinámico. Específicamente, dividieron la mayoría de los potenciales termodinámicos en términos clásicos y electrostáticos:

{displaystyle Phi =S-{frac {U}{T}}=-{frac {A}{T}},}

${displaystyle Phi }$ es Helmholtz libre entropía,
${displaystyle S}$ es entropía,
${displaystyle U}$ es energía interna,
${displaystyle T}$ es temperatura,
${displaystyle A}$ es Helmholtz energía libre.

D.H da el diferencial total ${displaystyle Phi }$ como

{displaystyle dPhi ={frac {P}{T}},dV+{frac {U}{T^{2}}},dT,}

${displaystyle P}$ es presión,
${displaystyle V}$ es volumen.

Por la definición del diferencial total, esto significa que

{displaystyle {frac {P}{T}}={frac {partial Phi }{partial V}},}

{displaystyle {frac {U}{T^{2}}}={frac {partial Phi }{partial T}},}

Como se indicó anteriormente, la energía interna se divide en dos partes:

{displaystyle U=U_{k}+U_{e}}

${displaystyle k}$ indica la parte clásica,
${displaystyle e}$ indica la parte eléctrica.

Del mismo modo, la entropía libre de Helmholtz también se divide en dos partes:

{displaystyle Phi =Phi _{k}+Phi _{e}.}

D&H afirma, sin dar la lógica, que

{displaystyle Phi _{e}=int {frac {U_{e}}{T^{2}}},dT.}

Parecería que, sin justificación alguna,

{displaystyle Phi _{e}=int {frac {P_{e}}{T}},dV+int {frac {U_{e}}{T^{2}}},dT.}

Sin mencionarlo específicamente, D plagaH más tarde dar lo que podría ser la justificación requerida (sobre) mientras argumenta que ${displaystyle Phi _{e}=Xi _{e}}$ , una suposición de que el solvente es incompresible.

La definición de la entropía libre de Gibbs ${displaystyle Xi }$ es

{displaystyle Xi =S-{frac {U+PV}{T}}=Phi -{frac {PV}{T}}=-{frac {G}{T}},}

{displaystyle G}

D.H da el diferencial total ${displaystyle Xi }$ como

{displaystyle dXi =-{frac {V}{T}},dP+{frac {U+PV}{T^{2}}},dT.}

En este punto Dю nota que, para el agua que contiene 1 mole por litro de cloruro de potasio (no se dan presión nominal y temperatura), la presión eléctrica ${displaystyle P_{e}}$ asciende a 20 ambientes. Además, observan que este nivel de presión da un cambio de volumen relativo de 0.001. Por lo tanto, descuidan el cambio en el volumen del agua debido a la presión eléctrica, escribiendo

{displaystyle Xi =Xi _{k}+Xi _{e},}

{displaystyle Xi _{e}=Phi _{e}=int {frac {U_{e}}{T^{2}}},dT.}

D&H dice que, según Planck, la parte clásica de la entropía libre de Gibbs es

{displaystyle Xi _{k}=sum _{i=0}^{s}N_{i}(xi _{i}-k_{text{B}}ln(x_{i})),}

${displaystyle i}$ es una especie,
${displaystyle s}$ es el número de diferentes tipos de partículas en solución,
${displaystyle N_{i}}$ es el número de partículas de especies i,
${displaystyle xi _{i}}$ es la partícula específica Gibbs entropía libre de especies i,
${displaystyle k_{text{B}}}$ es la constante de Boltzmann,
${displaystyle x_{i}}$ es la fracción del topo de las especies i.

Las especies cero son el solvente. La definición de ${displaystyle xi _{i}}$ es el siguiente, donde las letras minúsculas indican las versiones específicas de partículas de las propiedades extensas correspondientes:

{displaystyle xi _{i}=s_{i}-{frac {u_{i}+Pv_{i}}{T}}.}

No lo digas, pero la forma funcional para ${displaystyle Xi _{k}}$ puede derivarse de la dependencia funcional del potencial químico de un componente de una mezcla ideal sobre su fracción de mole.

Dю nota de que la energía interna ${displaystyle U}$ de una solución se reduce por la interacción eléctrica de sus iones, pero que este efecto no se puede determinar utilizando la aproximación cristalográfica para distancias entre átomos disimilares (la raíz del cubo de la relación del volumen total al número de partículas en el volumen). Esto es porque hay más movimiento térmico en una solución líquida que en un cristal. El movimiento térmico tiende a deshacerse de la celosía natural que de otro modo sería construido por los iones. En su lugar, D plaga introduce el concepto de un ambiente iónico o nube. Como la rejilla cristalina, cada ión todavía intenta rodearse de iones cargados opuestamente, pero de manera más libre; a pequeñas distancias lejos de iones positivos, uno es más probable encontrar iones negativos y viceversa.

La energía potencial de una solución iónica arbitraria

La electroneutralidad de una solución requiere que

{displaystyle sum _{i=1}^{s}N_{i}z_{i}=0,}

${displaystyle N_{i}}$ es el número total de iones de especies i en la solución,
${displaystyle z_{i}}$ es el número de carga de especies i.

Para traer un ión de especies i, inicialmente lejos, a un punto ${displaystyle P}$ dentro de la nube ion requiere energía de interacción en la cantidad de ${displaystyle z_{i}qvarphi }$ , donde ${displaystyle q}$ es la carga primaria, y ${displaystyle varphi }$ es el valor del campo potencial eléctrico de escalar en ${displaystyle P}$ . Si las fuerzas eléctricas fueran el único factor en juego, la configuración de energía mínima de todos los iones se lograría en una configuración de celosía muy ajustada. Sin embargo, los iones están en equilibrio térmico entre sí y son relativamente libres de moverse. Así obedecen las estadísticas Boltzmann y forman una distribución Boltzmann. Número de densidades de todas las especies ${displaystyle n_{i}}$ se alteran de sus valores de volumen (sobretodo promedio) ${displaystyle n_{i}^{0}}$ por el factor Boltzmann correspondiente ${displaystyle e^{-{frac {z_{i}qvarphi }{k_{text{B}}T}}}}$ , donde ${displaystyle k_{text{B}}}$ es la constante de Boltzmann, y ${displaystyle T}$ es la temperatura. Así en cada punto de la nube

{displaystyle n_{i}={frac {N_{i}}{V}}e^{-{frac {z_{i}qvarphi }{k_{text{B}}T}}}=n_{i}^{0}e^{-{frac {z_{i}qvarphi }{k_{text{B}}T}}}.}

Tenga en cuenta que en el límite de temperatura infinito, todos los iones se distribuyen uniformemente, sin tener en cuenta sus interacciones electrostáticas.

La densidad de carga está relacionada con la densidad numérica:

{displaystyle rho =sum _{i}z_{i}qn_{i}=sum _{i}z_{i}qn_{i}^{0}e^{-{frac {z_{i}qvarphi }{k_{text{B}}T}}}.}

Al combinar este resultado para la densidad de carga con la ecuación de Poisson de la electrostática, se obtiene una forma de la ecuación de Poisson-Boltzmann:

{displaystyle nabla ^{2}varphi =-{frac {rho }{varepsilon _{r}varepsilon _{0}}}=-sum _{i}{frac {z_{i}qn_{i}^{0}}{varepsilon _{r}varepsilon _{0}}}e^{-{frac {z_{i}qvarphi }{k_{text{B}}T}}}.}

Esta ecuación es difícil de resolver y no sigue el principio de superposición lineal para la relación entre el número de cargas y la intensidad del campo potencial. Ha sido resuelto por el matemático sueco Thomas Hakon Gronwall y sus colaboradores, los químicos físicos V. K. La Mer y Karl Sandved, en un artículo de 1928 de Physikalische Zeitschrift que trata sobre las extensiones de la teoría de Debye-Huckel, que recurrió a la expansión de la serie de Taylor.

Sin embargo, para concentraciones suficientemente bajas de iones, se puede utilizar una aproximación de expansión de la serie Taylor de primer orden para la función exponencial ( ${displaystyle e^{x}approx 1+x}$ para $<math alttext="{displaystyle 00c)x≪ ≪ 1{displaystyle 0 wonxll 1} <img alt="{displaystyle 0$ ) para crear una ecuación diferencial lineal (Hamann, Hamnett y Vielstich. Electroquímica. Wiley-VCH. section 2.4.2). DT dice que esta aproximación tiene grandes distancias entre iones, lo que es el mismo que decir que la concentración es baja. Por último, afirman sin pruebas que la adición de más términos en la expansión tiene poco efecto en la solución final. Así

{displaystyle -sum _{i}{frac {z_{i}qn_{i}^{0}}{varepsilon _{r}varepsilon _{0}}}e^{-{frac {z_{i}qvarphi }{k_{text{B}}T}}}approx -sum _{i}{frac {z_{i}qn_{i}^{0}}{varepsilon _{r}varepsilon _{0}}}left(1-{frac {z_{i}qvarphi }{k_{text{B}}T}}right)=-left(sum _{i}{frac {z_{i}qn_{i}^{0}}{varepsilon _{r}varepsilon _{0}}}-sum _{i}{frac {z_{i}^{2}q^{2}n_{i}^{0}varphi }{varepsilon _{r}varepsilon _{0}k_{text{B}}T}}right).}

La ecuación de Poisson-Boltzmann se transforma a

{displaystyle nabla ^{2}varphi =sum _{i}{frac {z_{i}^{2}q^{2}n_{i}^{0}varphi }{varepsilon _{r}varepsilon _{0}k_{text{B}}T}},}

Factorear el potencial de escalar y asignar las sobras, que son constantes, a ${displaystyle kappa ^{2}}$ . Además, deja ${displaystyle I}$ ser la fuerza iónica de la solución:

{displaystyle kappa ^{2}=sum _{i}{frac {z_{i}^{2}q^{2}n_{i}^{0}}{varepsilon _{r}varepsilon _{0}k_{text{B}}T}}={frac {2Iq^{2}}{varepsilon _{r}varepsilon _{0}k_{text{B}}T}},}

{displaystyle I={frac {1}{2}}sum _{i}z_{i}^{2}n_{i}^{0}.}

Entonces, la ecuación fundamental se reduce a una forma de ecuación de Helmholtz:

{displaystyle nabla ^{2}varphi =kappa ^{2}varphi.}

Hoy, ${displaystyle kappa ^{-1}}$ se llama la longitud de detección de Debye. D Pulh reconoce la importancia del parámetro en su artículo y lo caracteriza como una medida del espesor de la atmósfera ion, que es una capa doble eléctrica del tipo Gouy-Chapman.

La ecuación puede expresarse en coordenadas esféricas tomando ${displaystyle r=0}$ en algún ion arbitrario:

{displaystyle nabla ^{2}varphi ={frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}{frac {partial varphi (r)}{partial r}}right)={frac {partial ^{2}varphi (r)}{partial r^{2}}}+{frac {2}{r}}{frac {partial varphi (r)}{partial r}}=kappa ^{2}varphi (r).}

La ecuación tiene la siguiente solución general (tenga en cuenta que ${displaystyle kappa }$ es una constante positiva:

{displaystyle varphi (r)=A{frac {e^{-{sqrt {kappa ^{2}}}r}}{r}}+A'{frac {e^{{sqrt {kappa ^{2}}}r}}{2r{sqrt {kappa ^{2}}}}}=A{frac {e^{-kappa r}}{r}}+A''{frac {e^{kappa r}}{r}}=A{frac {e^{-kappa r}}{r}},}

{displaystyle A}

{displaystyle A'}

{displaystyle A''}

El potencial eléctrico es cero en el infinito por definición, así que ${displaystyle A''}$ debe ser cero.

En el siguiente paso, D.H. asume que hay un radio determinado ${displaystyle a_{i}}$ , más allá de lo cual ningún iones en la atmósfera puede acercarse al centro (cargo) del ión. Este radio puede ser debido al tamaño físico del ión mismo, los tamaños de los iones en la nube, y cualquier molécula de agua que rodea los iones. Matemáticamente, tratan al iión soltero como una carga de punto a la que uno no puede acercarse dentro del radio ${displaystyle a_{i}}$ .

El potencial de una carga puntual por sí sola es

{displaystyle varphi _{text{pc}}(r)={frac {1}{4pi varepsilon _{r}varepsilon _{0}}}{frac {z_{i}q}{r}}.}

D&H dice que el potencial total dentro de la esfera es

{displaystyle varphi _{text{sp}}(r)=varphi _{text{pc}}(r)+B_{i}={frac {1}{4pi varepsilon _{r}varepsilon _{0}}}{frac {z_{i}q}{r}}+B_{i},}

{displaystyle B_{i}}

{displaystyle B_{i}}

{displaystyle r}

{displaystyle a_{i}}

En una combinación del modelo continuamente distribuido que dio la ecuación Poisson-Boltzmann y el modelo de la carga de punto, se supone que en el radio ${displaystyle a_{i}}$ , hay una continuidad ${displaystyle varphi (r)}$ y su primer derivado. Así

{displaystyle varphi (a_{i})=A_{i}{frac {e^{-kappa a_{i}}}{a_{i}}}={frac {1}{4pi varepsilon _{r}varepsilon _{0}}}{frac {z_{i}q}{a_{i}}}+B_{i}=varphi _{text{sp}}(a_{i}),}

{displaystyle varphi '(a_{i})=-{frac {A_{i}e^{-kappa a_{i}}(1+kappa a_{i})}{a_{i}^{2}}}=-{frac {1}{4pi varepsilon _{r}varepsilon _{0}}}{frac {z_{i}q}{a_{i}^{2}}}=varphi _{text{sp}}'(a_{i}),}

{displaystyle A_{i}={frac {z_{i}q}{4pi varepsilon _{r}varepsilon _{0}}}{frac {e^{kappa a_{i}}}{1+kappa a_{i}}},}

{displaystyle B_{i}=-{frac {z_{i}qkappa }{4pi varepsilon _{r}varepsilon _{0}}}{frac {1}{1+kappa a_{i}}}.}

Por la definición de la energía potencial eléctrica, la energía potencial asociada con el iión desaparecido en la atmósfera ion es

{displaystyle u_{i}=z_{i}qB_{i}=-{frac {z_{i}^{2}q^{2}kappa }{4pi varepsilon _{r}varepsilon _{0}}}{frac {1}{1+kappa a_{i}}}.}

Observe que esto sólo requiere conocer la carga del ion seleccionado y el potencial de todos los demás iones.

Para calcular la energía potencial de toda la solución de electrolito, se debe utilizar la generalización de cargas múltiples para la energía potencial eléctrica:

{displaystyle U_{e}={frac {1}{2}}sum _{i=1}^{s}N_{i}u_{i}=-sum _{i=1}^{s}{frac {N_{i}z_{i}^{2}}{2}}{frac {q^{2}kappa }{4pi varepsilon _{r}varepsilon _{0}}}{frac {1}{1+kappa a_{i}}}.}

El término eléctrico adicional al potencial termodinámico

No dimensionalización

La ecuación diferencial está lista para solución (como se indicó anteriormente, la ecuación solo es válida para concentraciones bajas):

{displaystyle {frac {partial ^{2}varphi (r)}{partial r^{2}}}+{frac {2}{r}}{frac {partial varphi (r)}{partial r}}={frac {Iqvarphi (r)}{varepsilon _{r}varepsilon _{0}k_{text{B}}T}}=kappa ^{2}varphi (r).}

Usar el teorema π de Buckingham en este problema da como resultado los siguientes grupos adimensionales:

{displaystyle {begin{aligned}pi _{1}&={frac {qvarphi (r)}{k_{text{B}}T}}=Phi (R(r))\pi _{2}&=varepsilon _{r}\pi _{3}&={frac {ak_{text{B}}Tvarepsilon _{0}}{q^{2}}}\pi _{4}&=a^{3}I\pi _{5}&=z_{0}\pi _{6}&={frac {r}{a}}=R(r).end{aligned}}}

{displaystyle Phi }

{displaystyle R}

{displaystyle (kappa a)^{2}}

{displaystyle Z_{0}}

{displaystyle z_{0}}

{displaystyle {frac {pi _{4}}{pi _{2}pi _{3}}}={frac {a^{2}q^{2}I}{varepsilon _{r}varepsilon _{0}k_{text{B}}T}}=(kappa a)^{2}}

{displaystyle {frac {pi _{5}}{pi _{2}pi _{3}}}={frac {z_{0}q^{2}}{4pi avarepsilon _{r}varepsilon _{0}k_{text{B}}T}}=Z_{0}}

Para obtener la ecuación diferencial no dimensionada y las condiciones iniciales, utilice la ${displaystyle pi }$ grupos para eliminar ${displaystyle varphi (r)}$ a favor de ${displaystyle Phi (R(r))}$ , luego eliminar ${displaystyle R(r)}$ a favor de ${displaystyle r}$ mientras realiza la regla de la cadena y sustituye ${displaystyle {R^{prime }}(r)=a}$ , luego eliminar ${displaystyle r}$ a favor de ${displaystyle R}$ (no se necesita una regla de cadena), luego eliminar ${displaystyle I}$ a favor de ${displaystyle (kappa a)^{2}}$ , luego eliminar ${displaystyle z_{0}}$ a favor de ${displaystyle Z_{0}}$ . Las ecuaciones resultantes son las siguientes:

{displaystyle {frac {partial Phi (R)}{partial R}}{bigg |}_{R=1}=-Z_{0}}

{displaystyle Phi (infty)=0}

{displaystyle {frac {partial ^{2}Phi (R)}{partial R^{2}}}+{frac {2}{R}}{frac {partial Phi (R)}{partial R}}=(kappa a)^{2}Phi (R).}

Para la sal de mesa en la solución 0.01 M a 25 °C, un valor típico de ${displaystyle (kappa a)^{2}}$ es 0.0005636, mientras que un valor típico de ${displaystyle Z_{0}}$ es 7.017, destacando el hecho de que, en bajas concentraciones, ${displaystyle (kappa a)^{2}}$ es un objetivo para un orden cero de aproximación de magnitud, como el análisis de perturbación. Lamentablemente, debido a la condición de límite en el infinito, la perturbación regular no funciona. La misma condición límite nos impide encontrar la solución exacta a las ecuaciones. Sin embargo, la perturbación singular puede funcionar.

Verificación experimental de la teoría

Para verificar la validez de la teoría de Debye-Hückel, se han probado muchas formas experimentales, midiendo los coeficientes de actividad: el problema es que debemos ir hacia diluciones muy altas. Ejemplos típicos son: mediciones de presión de vapor, punto de congelación, presión osmótica (métodos indirectos) y medición del potencial eléctrico en celdas (método directo). Hacia diluciones altas se han encontrado buenos resultados usando celdas de membrana líquida, se ha podido investigar medios acuosos 10⁻⁴ M y se ha encontrado que para electrolitos 1:1 (como NaCl o KCl) La ecuación de Debye-Hückel es totalmente correcta, pero para electrolitos 2:2 o 3:2 es posible encontrar una desviación negativa de la ley límite de Debye-Hückel: este extraño comportamiento sólo se puede observar en el área muy diluida, y en más En las regiones concentradas la desviación se vuelve positiva. Es posible que la ecuación de Debye-Hückel no sea capaz de prever este comportamiento debido a la linealización de la ecuación de Poisson-Boltzmann, o tal vez no: los estudios al respecto se iniciaron sólo durante los últimos años del siglo XX porque antes no era No es posible investigar la región 10⁻⁴ M, por lo que es posible que durante los próximos años nazcan nuevas teorías.

Extensiones de la teoría

Se han propuesto varios enfoques para extender la validez de la ley a rangos de concentración que se encuentran comúnmente en química.

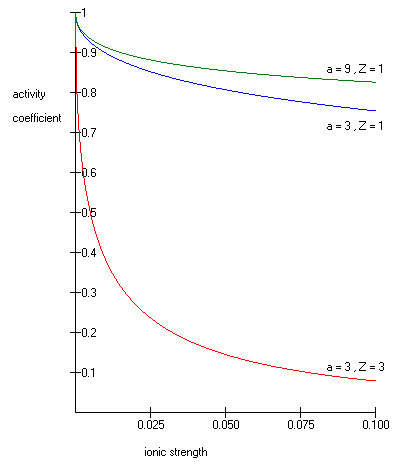
Una de esas ecuaciones extendidas de Debye-Hückel viene dada por:

{displaystyle -log _{10}(gamma)={frac {A|z_{+}z_{-}|{sqrt {I}}}{1+Ba{sqrt {I}}}}}

{displaystyle gamma }

{displaystyle z}

⁺²⁺

{displaystyle I}

{displaystyle a}

diámetro efectivo⁺⁻⁻⁻

{displaystyle A}

{displaystyle B}

La ecuación extendida de Debye-Hückel proporciona resultados precisos para μ ≤ 0,1. Para soluciones de mayor fuerza iónica, se deben utilizar las ecuaciones de Pitzer. En estas soluciones, el coeficiente de actividad puede aumentar con la fuerza iónica.

The Debye–Hückel plot with different values for ion charge Z and ion diameter a — La trama Debye-Hückel con diferentes valores de carga ion Z y diámetro ion a

La ecuación de Debye-Hückel no se puede utilizar en soluciones de tensioactivos donde la presencia de micelas influye en las propiedades electroquímicas del sistema (incluso un juicio aproximado sobreestima γ en ~50%).

Más resultados...