Ecuación de Arrhenius

Ajustar Compartir Imprimir Citar

Fórmula para la dependencia de temperatura de las tasas de reacciones químicas

En química física, la ecuación de Arrhenius es una fórmula para la dependencia de la temperatura de las velocidades de reacción. La ecuación fue propuesta por Svante Arrhenius en 1889, basada en el trabajo del químico holandés Jacobus Henricus van 't Hoff, quien había notado en 1884 que la ecuación de van 't Hoff para la dependencia de la temperatura de las constantes de equilibrio sugiere tal una fórmula para las velocidades de las reacciones directa e inversa. Esta ecuación tiene una amplia e importante aplicación para determinar la velocidad de las reacciones químicas y para el cálculo de la energía de activación. Arrhenius proporcionó una justificación física y una interpretación de la fórmula. Actualmente, se ve mejor como una relación empírica. Se puede usar para modelar la variación de temperatura de los coeficientes de difusión, la población de vacantes de cristal, las tasas de fluencia y muchos otros procesos/reacciones inducidos térmicamente. La ecuación de Eyring, desarrollada en 1935, también expresa la relación entre velocidad y energía.

Ecuación

En casi todos los casos prácticos,

{displaystyle E_{a}gg RT}

y k aumenta rápidamente T.

Matemáticamente, a temperaturas muy altas para que

{displaystyle E_{a}ll RT}

, k y enfoques A como límite, pero este caso no ocurre en condiciones prácticas.

La ecuación de Arrhenius da la dependencia de la constante de velocidad de una reacción química en la temperatura absoluta como

{displaystyle k=Ae^{frac {-E_{rm {a}}}{RT}},}

$k$ es la frecuencia constante (frecuencia de colisiones que resulta en una reacción),
$T$ es la temperatura absoluta (en Kelvin o grado Rankine),
$A$ es el factor pre-exponencial. Arrhenius originalmente considerado A para ser una constante dependiente de temperatura para cada reacción química. Sin embargo, tratamientos más recientes incluyen cierta dependencia de temperatura - ver la ecuación de arrienio modificada abajo.
$E a$ es la energía de activación para la reacción (en las mismas unidades que RT),
$R$ es la constante de gas universal.

Alternativamente, la ecuación se puede expresar como

{displaystyle k=Ae^{frac {-E_{rm {a}}}{k_{rm {B}}T}},}

$E a$ es la energía de activación para la reacción (en las mismas unidades que k_BT),
$k B$ es la constante de Boltzmann.

La única diferencia son las unidades de energía de $E a$ : la primera forma usa energía por mol, que es común en química, mientras que la última forma usa energía por molécula directamente, lo cual es común en física. Las diferentes unidades se tienen en cuenta utilizando la constante de gas, $R$ , o la constante de Boltzmann, $k B$ , como el multiplicador de temperatura $T$ .

Las unidades del factor pre-exponencial $A$ son idénticos a los de la frecuencia constante y variarán dependiendo del orden de la reacción. Si la reacción es primera orden tiene las unidades: s⁻¹, y por eso se llama a menudo factor de frecuencia o frecuencia de intento de la reacción. Simplemente, $k$ es el número de colisiones que dan lugar a una reacción por segundo, $A$ es el número de colisiones (saliendo a una reacción o no) por segundo ocurre con la orientación adecuada para reaccionar y ${displaystyle e^{-E_{rm {a}}/(RT)}}$ es la probabilidad de que cualquier colisión dada resulte en una reacción. Se puede ver que el aumento de la temperatura o la disminución de la energía de activación (por ejemplo, mediante el uso de catalizadores) dará lugar a un aumento de la tasa de reacción.

Dada la pequeña temperatura de los estudios cinéticos, es razonable aproximar la energía de activación como independiente de la temperatura. Asimismo, bajo una amplia gama de condiciones prácticas, la débil dependencia de temperatura del factor pre-exponencial es insignificante en comparación con la dependencia de temperatura de la ${displaystyle exp(-E_{rm {a}}/(RT))}$ factor; excepto en el caso de reacciones "sin barreras" limitadas a la difusión, en cuyo caso el factor pre-exponencial es dominante y es directamente observable.

Con esta ecuación, se puede estimar aproximadamente que la velocidad de reacción aumenta en un factor de aproximadamente 2 o 3 por cada aumento de temperatura de 10 °C.

El término ${displaystyle e^{frac {-E_{a}}{RT}}}$ denota la fracción de moléculas con energía mayor o igual a $E_{a}$ .

Gráfico de Arrhenius

Parcela lineal de arrienio: lnk contra 1/T.

Tomando el logaritmo natural de la ecuación de Arrhenius se obtiene:

{displaystyle ln k=ln A-{frac {E_{rm {a}}}{R}}{frac {1}{T}}.}

Reorganización de los rendimientos:

{displaystyle ln k={frac {-E_{rm {a}}}{R}}left({frac {1}{T}}right)+ln A.}

Tiene la misma forma que una ecuación para una línea recta:

{displaystyle y=mx+c,}

donde x es el recíproco de T.

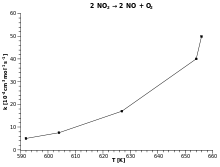
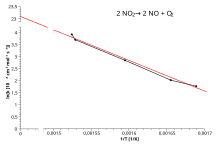
Entonces, cuando una reacción tiene una constante de velocidad que obedece a la ecuación de Arrhenius, una gráfica de ln k versus T⁻¹ da un recta, cuya pendiente e intersección se pueden usar para determinar E_a y A. Este procedimiento se ha vuelto tan común en la cinética química experimental que los profesionales han comenzado a utilizarlo para definir la energía de activación de una reacción. Es decir, la energía de activación se define como (−R) veces la pendiente de un gráfico de ln k frente a (1/T):

{displaystyle E_{rm {a}}equiv -Rleft[{frac {partial ln k}{partial (1/T)}}right]_{P}.}

Ecuación de Arrhenius modificada

La ecuación de Arrhenius modificada hace explícita la dependencia de la temperatura del factor preexponencial. La ecuación modificada suele tener la forma

{displaystyle k=AT^{n}e^{-E_{rm {a}}/(RT)}.}

La expresión original de Arrhenius anterior corresponde a n = 0. Las constantes de tasa ajustada normalmente se encuentran en el rango −1 < n < 1. Los análisis teóricos arrojan varias predicciones para n. Se ha señalado que "no es factible establecer, sobre la base de estudios de temperatura de la constante de velocidad, si la dependencia T^1/2 predicha del factor pre-exponencial se observa experimentalmente". Sin embargo, si se dispone de evidencia adicional, de la teoría y/o del experimento (como la dependencia de la densidad), no hay obstáculo para las pruebas incisivas de la ley de Arrhenius.

Otra modificación común es la forma exponencial estirada

{displaystyle k=Aexp left[-left({frac {E_{a}}{RT}}right)^{beta }right],}

donde β es un número adimensional de orden 1. Por lo general, esto se considera una corrección puramente empírica o un factor de elusión para hacer que el modelo se ajuste a los datos, pero puede tener significado teórico, por ejemplo mostrando la presencia de un rango de energías de activación o en casos especiales como el salto de rango variable de Mott.

Interpretación teórica de la ecuación

El concepto de energía de activación de Arrhenius

Arrhenius argumentó que para que los reactivos se transformen en productos, primero deben adquirir una cantidad mínima de energía, llamada energía de activación E_a. A una temperatura absoluta T, la fracción de moléculas que tienen una energía cinética mayor que E_a se puede calcular a partir de la mecánica estadística. El concepto de energía de activación explica el carácter exponencial de la relación, y de una forma u otra, está presente en todas las teorías cinéticas.

Los cálculos para las constantes de velocidad de reacción implican un promedio de energía sobre una distribución Maxwell-Boltzmann con ${displaystyle E_{rm {a}}}$ como límite inferior y así son a menudo del tipo de funciones gamma incompleta, que resulta ser proporcional a ${displaystyle e^{frac {-E_{rm {a}}}{RT}}}$ .

Teoría de colisiones

Un enfoque es la teoría de la colisión de las reacciones químicas, desarrollada por Max Trautz y William Lewis en los años 1916–18. En esta teoría, se supone que las moléculas reaccionan si chocan con una energía cinética relativa a lo largo de su línea de centros que excede E_a. Se encuentra que el número de colisiones binarias entre dos moléculas diferentes por segundo por unidad de volumen es

{displaystyle z_{AB}=N_{rm {A}}d_{AB}^{2}{sqrt {frac {8pi k_{rm {B}}T}{mu _{AB}}}},}

N_Ad_ABABTk_Bμ_AB

La constante de tasa se calcula entonces como ${displaystyle k=z_{AB}e^{frac {-E_{rm {a}}}{RT}},}$ así que la teoría de la colisión predice que el factor pre-exponencial es igual al número de colisión z_AB. Sin embargo, para muchas reacciones esto está de acuerdo mal con el experimento, por lo que la constante de tasa está escrita como ${displaystyle k=rho z_{AB}e^{frac {-E_{rm {a}}}{RT}},}$ . Aquí. $rho$ es un factor esterico empírico, a menudo mucho menos de 1.00, que se interpreta como la fracción de colisiones suficientemente energéticas en las que las dos moléculas tienen la orientación mutua correcta para reaccionar.

Teoría del estado de transición

La ecuación de Eyring, otra expresión similar a la de Arrhenius, aparece en la "teoría del estado de transición" de reacciones químicas, formulado por Wigner, Eyring, Polanyi y Evans en la década de 1930. La ecuación de Eyring se puede escribir:

{displaystyle k={frac {k_{rm {B}}T}{h}}e^{-{frac {Delta G^{ddagger }}{RT}}}={frac {k_{rm {B}}T}{h}}e^{frac {Delta S^{ddagger }}{R}}e^{-{frac {Delta H^{ddagger }}{RT}}},}

Donde $Delta G^{ddagger }$ es la energía Gibbs de activación, $Delta S^{ddagger }$ es la entropía de la activación, ${displaystyle Delta H^{ddagger }}$ es la enthalpy de la activación, $k_{rm B}$ es la constante de Boltzmann, y $h$ Es constante de Planck.

A primera vista esto parece un exponencial multiplicado por un factor que es lineal a temperatura. Sin embargo, la energía libre es en sí misma una cantidad dependiente de la temperatura. La energía libre de activación ${displaystyle Delta G^{ddagger }=Delta H^{ddagger }-TDelta S^{ddagger }}$ es la diferencia de un término enthalpy y un término entropía multiplicado por la temperatura absoluta. El factor pre-exponencial depende principalmente de la entropía de la activación. La expresión general de nuevo toma la forma de un exponencial de Arrienio (de enthalpy en lugar de energía) multiplicado por una función lentamente variable de T. La forma precisa de la dependencia de temperatura depende de la reacción, y se puede calcular utilizando fórmulas de mecánica estadística que implican las funciones de partición de los reaccionarios y del complejo activo.

Limitaciones de la idea de la energía de activación de Arrhenius

Tanto la energía de activación de Arrhenius como la constante de velocidad k se determinan experimentalmente y representan parámetros macroscópicos específicos de la reacción que no están simplemente relacionados con las energías de umbral y el éxito de las colisiones individuales a nivel molecular. Considere una colisión particular (una reacción elemental) entre las moléculas A y B. El ángulo de colisión, la energía de traslación relativa, la energía interna (particularmente vibracional) determinarán la probabilidad de que la colisión produzca una molécula producto AB. Las mediciones macroscópicas de E y k son el resultado de muchas colisiones individuales con diferentes parámetros de colisión. Para probar las velocidades de reacción a nivel molecular, los experimentos se realizan en condiciones cercanas a la colisión y este tema a menudo se denomina dinámica de reacción molecular.

Otra situación en la que la explicación de los parámetros de la ecuación de Arrhenius se queda corta es en la catálisis heterogénea, especialmente para las reacciones que muestran la cinética de Langmuir-Hinshelwood. Claramente, las moléculas en las superficies no "colisionan" directamente, y una sección transversal molecular simple no se aplica aquí. En cambio, el factor preexponencial refleja el viaje a través de la superficie hacia el sitio activo.

Hay desviaciones de la ley de Arrhenius durante la transición vítrea en todas las clases de materia vítrea. La ley de Arrhenius predice que el movimiento de las unidades estructurales (átomos, moléculas, iones, etc.) debería disminuir a un ritmo más lento durante la transición vítrea de lo que se observa experimentalmente. En otras palabras, las unidades estructurales se ralentizan a un ritmo más rápido de lo previsto por la ley de Arrhenius. Esta observación se hace razonable asumiendo que las unidades deben superar una barrera energética por medio de una energía de activación térmica. La energía térmica debe ser lo suficientemente alta para permitir el movimiento de traslación de las unidades que conduce al flujo viscoso del material.

Te puede interesar
Constante de faraday
(leer más)
Te puede interesar
La ley de graham
(leer más)
Te puede interesar
Ecuación de Nernst
(leer más)
Más resultados...