Dual space...

AjustarCompartirImprimirCitar

En matemáticas, espacio vectorial de formas lineales

En matemáticas, cualquier espacio vectorial $V$ tiene un correspondiente espacio vectorial dual (o simplemente espacio dual para abreviar) que consiste en todas las formas lineales $V$ , junto con la estructura espacial vectorial de la adición de punta y la multiplicación de escalar por constantes.

El espacio dual como se define arriba se define para todos los espacios vectoriales y, para evitar ambigüedades, también puede llamarse espacio dual algebraico. Cuando se define para un espacio vectorial topológico, existe un subespacio del espacio dual, correspondiente a los funcionales lineales continuos, denominado espacio dual continuo.

Los espacios vectoriales duales encuentran aplicación en muchas ramas de las matemáticas que utilizan espacios vectoriales, como en el análisis tensorial con espacios vectoriales de dimensión finita. Cuando se aplica a espacios vectoriales de funciones (que suelen ser de dimensión infinita), los espacios duales se utilizan para describir medidas, distribuciones y espacios de Hilbert. En consecuencia, el espacio dual es un concepto importante en el análisis funcional.

Los primeros términos para dual incluyen polarer Raum [Hahn 1927], espace conjugué, adjoint space [Alaoglu 1940], y transponierter Raum [Schauder 1930] y [Banach 1932]. El término dual se debe a Bourbaki 1938.

Espacio dual algebraico

Dado cualquier espacio vectorial $V$ sobre un terreno $F$ , el (algebraica) espacio dual ${displaystyle V^{*}}$ (alternatively denoted by ${displaystyle V^{lor }}$ o $V'$ ) se define como el conjunto de todos los mapas lineales ${displaystyle varphi:Vto F}$ (funcionales lineales). Puesto que los mapas lineales son homomorfismos espaciales vectoriales, el espacio dual puede ser denotado ${displaystyle hom(V,F)}$ . El espacio dual $V^{*}$ se convierte en un espacio vectorial sobre $F$ cuando está equipado con una adición y multiplicación de escalar satisfactoria:

{displaystyle {begin{aligned}(varphi +psi)(x)&=varphi (x)+psi (x)\(avarphi)(x)&=aleft(varphi (x)right)end{aligned}}}

para todos ${displaystyle varphipsi in V^{*}}$ , $xin V$ , y $ain F$ .

Elementos del espacio dual algebraico $V^{*}$ a veces se llama covectores o una forma.

El emparejamiento de un funcional $varphi$ en el espacio dual $V^{*}$ y un elemento $x$ de $V$ a veces se denota por un corchete: ${displaystyle varphi (x)=[x,varphi ]}$ o ${displaystyle varphi (x)=langle x,varphi rangle }$ . Este pareado define un mapeo bilineal nodegenerado ${displaystyle langle cdotcdot rangle:Vtimes V^{*}to F}$ llamó a la pareja natural.

Caso de dimensión finita

Si V es de dimensión finita, entonces V^∗ tiene la misma dimensión que V. Dada una base ${e 1,..., e n}$ en V, es posible construir una base específica en V^∗, llamada doble base. Esta base dual es un conjunto ${e 1,..., e n}$ de funcionales lineales en V, definidos por la relación

mathbf{e}^i(c^1 mathbf{e}_1+cdots+c^nmathbf{e}_n) = c^i, quad i=1,ldots,n

para cualquier elección de coeficientes $c i \in F$ . En particular, dejando a su vez que cada uno de esos coeficientes sea igual a uno y los otros coeficientes cero, da el sistema de ecuaciones

mathbf{e}^i(mathbf{e}_j) = delta^{i}_{j}

Donde $delta^{i}_{j}$ es el símbolo Kronecker delta. Esta propiedad se denomina propiedad bi-ortogonalidad.

Prueba
Considerar ${} e 1,... e n$ } la base de V. Vamos ${} e 1,... e n$ } se define como el siguiente: $mathbf{e}^i(c^1 mathbf{e}_1+cdots+c^nmathbf{e}_n) = c^i, quad i=1,ldots,n$ . Tenemos: ${displaystyle e^{i},i=1,2,dotsn,}$ son funcionales lineales. De hecho, para ${displaystyle x,yin V}$ tales como ${displaystyle x=alpha _{1}e_{1}+dots +alpha _{n}e_{n}}$ y ${displaystyle y=beta _{1}e_{1}+dots +beta _{n}e_{n}}$ (es decir, ${displaystyle e^{i}(x)=alpha _{i}}$ y ${displaystyle e^{i}(y)=beta _{i}}$ ). Entonces, ${displaystyle x+lambda y=(alpha _{1}+lambda beta _{1})e_{1}+dots +(alpha _{n}+lambda beta _{n})e_{n}}$ y ${displaystyle e^{i}(x+lambda y)=alpha _{i}+lambda beta _{i}=e^{i}(x)+lambda e^{i}(y)}$ . Por lo tanto, ${displaystyle e^{i}in V^{}}$ para ${displaystyle i=1,2,dotsn}$ . Suppose ${displaystyle lambda _{1}e^{1}+cdots +lambda _{n}e^{n}=0in V^{}}$ . Aplicar esta funcionalidad sobre la base de vectores $V$ sucesivamente, nos lleva a ${displaystyle lambda _{1}=lambda _{2}=dots =lambda _{n}=0}$ (El funcional aplicado en $e_i$ resultados en $lambda _{i}$ ). Por lo tanto, ${} e 1,... e n$ } is l.i. on ${displaystyle V^{}}$ . Por último, considerar ${displaystyle gin V^{}}$ . Entonces... ${displaystyle g(x)=g(alpha _{1}e_{1}+dots +alpha _{n}e_{n})=alpha _{1}g(e_{1})+dots +alpha _{n}g(e_{n})=e^{1}(x)g(e_{1})+dots +e^{n}(x)g(e_{n})}$ y ${} e 1,... e n$ } genera $V^{}$ . Por lo tanto, es la base de ${displaystyle V^{}}$ .

Prueba

Considerar ${} e 1,... e n$ } la base de V. Vamos ${} e 1,... e n$ } se define como el siguiente:

$mathbf{e}^i(c^1 mathbf{e}_1+cdots+c^nmathbf{e}_n) = c^i, quad i=1,ldots,n$ .

Tenemos:

${displaystyle e^{i},i=1,2,dotsn,}$ son funcionales lineales. De hecho, para ${displaystyle x,yin V}$ tales como ${displaystyle x=alpha _{1}e_{1}+dots +alpha _{n}e_{n}}$ y ${displaystyle y=beta _{1}e_{1}+dots +beta _{n}e_{n}}$ (es decir, ${displaystyle e^{i}(x)=alpha _{i}}$ y ${displaystyle e^{i}(y)=beta _{i}}$ ). Entonces, ${displaystyle x+lambda y=(alpha _{1}+lambda beta _{1})e_{1}+dots +(alpha _{n}+lambda beta _{n})e_{n}}$ y ${displaystyle e^{i}(x+lambda y)=alpha _{i}+lambda beta _{i}=e^{i}(x)+lambda e^{i}(y)}$ . Por lo tanto, ${displaystyle e^{i}in V^{*}}$ para ${displaystyle i=1,2,dotsn}$ .
Suppose ${displaystyle lambda _{1}e^{1}+cdots +lambda _{n}e^{n}=0in V^{*}}$ . Aplicar esta funcionalidad sobre la base de vectores $V$ sucesivamente, nos lleva a ${displaystyle lambda _{1}=lambda _{2}=dots =lambda _{n}=0}$ (El funcional aplicado en $e_i$ resultados en $lambda _{i}$ ). Por lo tanto, ${} e 1,... e n$ } is l.i. on ${displaystyle V^{*}}$ .
Por último, considerar ${displaystyle gin V^{*}}$ . Entonces...

{displaystyle g(x)=g(alpha _{1}e_{1}+dots +alpha _{n}e_{n})=alpha _{1}g(e_{1})+dots +alpha _{n}g(e_{n})=e^{1}(x)g(e_{1})+dots +e^{n}(x)g(e_{n})}

y ${} e 1,... e n$ } genera $V^{*}$ . Por lo tanto, es la base de ${displaystyle V^{*}}$ .

Por ejemplo, si V es R², deje que su base se elija como ${e 1 = (1/2, 1/2), e 2 = (0, 1)}. Los vectores base no son ortogonales entre sí. Entonces, e 1 y e 2 son formas únicas (funciones que asignan un vector a un escalar) tales que e 1 (e 1) = 1, e 1 (e 2) = 0, e 2 (e 1) = 0$ , y e²(e₂) = 1. (Nota: el superíndice aquí es el índice, no un exponente). Este sistema de ecuaciones se puede expresar usando notación matricial como

{displaystyle {begin{bmatrix}e_{11}&e_{12}\e_{21}&e_{22}end{bmatrix}}{begin{bmatrix}e^{11}&e^{21}\e^{12}&e^{22}end{bmatrix}}={begin{bmatrix}1&0\0&1end{bmatrix}}.}

Resolver esta ecuación muestra que la base dual es ${e 1 = (2, 0), e 2 = (-1, 1)}$ . Como e¹ y e² son funcionales, se pueden reescribir como e ¹(x, y) = 2x y e²(x, y) = −x + y. En general, cuando V es Rⁿ, si E = (e₁,..., e_n) es una matriz cuyas columnas son las vectores base y Ê = (e¹,..., eⁿ) es una matriz cuyas columnas son los vectores de base dual, entonces

{displaystyle E^{T}{hat {E}}=I_{n},}

donde I_n es una matriz identidad de orden $n$ . La propiedad de biortogonalidad de estos dos conjuntos de bases permite que cualquier punto x ∈ V se represente como

{displaystyle mathbf {x} =sum _{i}langle mathbf {x}mathbf {e} ^{i}rangle mathbf {e} _{i}=sum _{i}langle mathbf {x}mathbf {e} _{i}rangle mathbf {e} ^{i},}

incluso cuando los vectores base no son ortogonales entre sí. Strictly speaking, the above statement only makes sense once the internal product $langle cdotcdot rangle$ y el emparejamiento de la dualidad correspondiente se introduce, como se describe a continuación § Productos bilineales y espacios duales.

En particular, Rⁿ puede interpretarse como el espacio de columnas de $n$ números reales, su espacio dual generalmente se escribe como el espacio de filas de $n$ números reales. Tal fila actúa sobre Rⁿ como un funcional lineal por multiplicación de matrices ordinaria. Esto se debe a que una función mapea cada $n$ -vector x en un número real y. Luego, viendo este funcional como una matriz M, y x, y como un $n \times 1$ matriz y $1 \times 1$ (trivialmente, un número real) respectivamente, si $Mx = y$ entonces, por razones de dimensión, M debe ser $1 \times n$ matriz; es decir, M debe ser un vector fila.

Si V consiste en el espacio de vectores geométricos en el plano, entonces las curvas de nivel de un elemento de V^∗ forman una familia de líneas paralelas en V, porque el rango es unidimensional, de modo que cada punto en el rango es un múltiplo de cualquier elemento distinto de cero. Entonces, un elemento de V^∗ puede pensarse intuitivamente como una familia particular de líneas paralelas que cubren el plano. Para calcular el valor de un funcional en un vector dado, basta con determinar en cuál de las líneas se encuentra el vector. Informalmente, esto "cuenta" cuantas rectas cruza el vector. Más generalmente, si V es un espacio vectorial de cualquier dimensión, entonces los conjuntos de niveles de un funcional lineal en V^∗ son hiperplanos paralelos en V, y la acción de un funcional lineal sobre un vector se puede visualizar en términos de estos hiperplanos.

Caso de dimensión infinita

Si V no es de dimensión finita pero tiene una base e_α indexada por un conjunto infinito A, entonces la misma construcción que en el caso de dimensión finita produce elementos linealmente independientes e^α ( $α \in A$ ) del espacio dual, pero no formarán una base.

Por ejemplo, el espacio R^∞, cuyos elementos son aquellas secuencias de números reales que contienen solo un número finito de entradas distintas de cero, que tiene una base indexada por el números naturales N: para $i \in N$ , e _i es la secuencia que consta de todos ceros excepto en la posición i-ésima, que es 1. El espacio dual de R^∞ es (isomorfo a) R^N, el espacio de todos secuencias de números reales: cada secuencia real (a_n) define una función donde el elemento (x_n) de R^∞ se envía al número

{displaystyle sum _{n}a_{n}x_{n},}

que es una suma finita porque solo hay un número finito de x_n distintos de cero. La dimensión de R^∞ es contablemente infinita, mientras que R^N no tiene una base contable.

Esta observación se generaliza a cualquier espacio vectorial de dimensión infinita V sobre cualquier campo F: una elección de base ${e α : α \in A}$ identifica V con el espacio (F^A)₀ de funciones $f : A \to F$ tal que $f α = f (α)$ es distinto de cero solo para un número finito de $α \in A$ , donde tal una función f se identifica con el vector

{displaystyle sum _{alpha in A}f_{alpha }mathbf {e} _{alpha }}

en V (la suma es finita por la suposición de f, y cualquier $v \in V$ puede escribirse de esta manera por la definición de la base).

El espacio dual de V puede entonces identificarse con el espacio F^A de todas las funciones de A a F: un funcional lineal T en V está determinado únicamente por los valores $θ α = T (e α)$ se basa en V, y cualquier función $θ : A \to F$ (con $θ (α) = θ α$ ) define un funcional lineal T en V por

{displaystyle Tleft(sum _{alpha in A}f_{alpha }mathbf {e} _{alpha }right)=sum _{alpha in A}f_{alpha }T(e_{alpha })=sum _{alpha in A}f_{alpha }theta _{alpha }.}

Nuevamente, la suma es finita porque f_α es distinto de cero solo para un número finito de α.

El conjunto (F^A)₀ puede identificarse (esencialmente por definición) con la suma directa de infinitas copias de F (visto como un espacio vectorial unidimensional sobre sí mismo) indexado por A, es decir, hay isomorfismos lineales

{displaystyle Vcong (F^{A})_{0}cong bigoplus _{alpha in A}F.}

Por otro lado, F^A es (nuevamente por definición), el producto directo de infinitas copias de F indexadas por A, por lo que la identificación

{displaystyle V^{*}cong left(bigoplus _{alpha in A}Fright)^{*}cong prod _{alpha in A}F^{*}cong prod _{alpha in A}Fcong F^{A}}

es un caso especial de un resultado general que relaciona sumas directas (de módulos) con productos directos.

Considerando los números cardinales, indicados aquí como valores absolutos, se tiene un $F$ -espacio vectorial $V$ que tiene una base infinita $A$

<math alttext="{displaystyle |V|=max(|F|,|A|)SilencioVSilencio=max()SilencioFSilencio,SilencioASilencio).SilencioVAlternativa Alternativa Silencio=SilencioFSilencioSilencioASilencio.{displaystyle TENV WordPress=max(Principalmente, involuntariaA sometida) se llevó a cabo involuntariamente. <img alt="{displaystyle |V|=max(|F|,|A|)

Se sigue que, si un espacio vectorial no es de dimensión finita, entonces el axioma de elección implica que el espacio dual algebraico es siempre de mayor dimensión (como un número cardinal) que el vector original espacio (ya que, si dos bases tienen la misma cardinalidad, los espacios vectoriales generados tienen la misma cardinalidad). Esto contrasta con el caso del espacio dual continuo, discutido a continuación, que puede ser isomorfo al espacio vectorial original incluso si este último es de dimensión infinita.

Productos bilineales y espacios duales

Si V es de dimensión finita, entonces V es isomorfo a V^∗. Pero en general no hay isomorfismo natural entre estos dos espacios. Cualquier forma bilineal $⟨\cdot,\cdot⟩$ en V da un mapeo de V en su espacio dual a través de

vmapsto langle v, cdotrangle

donde el lado derecho se define como el funcional en V tomando cada $w \in V$ a $⟨ v, w ⟩$ . En otras palabras, la forma bilineal determina un mapeo lineal

Phi_{langlecdot,cdotrangle}: Vto V^*

definido por

{displaystyle left[Phi _{langle cdotcdot rangle }(v),wright]=langle v,wrangle.}

Si la forma bilineal es nodegenerada, entonces esto es un isomorfismo en un subespacio V^Alternativa. Si V es finito-dimensional, entonces esto es un isomorfismo sobre todo V^Alternativa. Por el contrario, cualquier isomorfismo $Phi$ desde V a un subespacio V^Alternativa (resp., all of V^Alternativa si V es finito dimensional) define una forma bilineal nondegenerada única ${displaystyle langle cdotcdot rangle _{Phi }}$ on V por

{displaystyle langle v,wrangle _{Phi }=(Phi (v))(w)=[Phi (v),w].,}

Por lo tanto, existe una correspondencia uno a uno entre los isomorfismos de V a un subespacio de (resp., todo de) V^∗ y formas bilineales no degeneradas en V.

Si el espacio vectorial V está sobre el campo complejo, a veces es más natural considerar formas sesquilineales en lugar de formas bilineales. En ese caso, una forma sesquilineal dada $⟨\cdot,\cdot⟩$ determina un isomorfismo de V con el complejo conjugado del espacio dual

{displaystyle Phi _{langle cdotcdot rangle }:Vto {overline {V^{*}}}.}

El conjugado del espacio dual ${displaystyle {overline {V^{*}}}}$ se puede identificar con el conjunto de todas las funciones aditivas de valor complejo $f : V \to C$ tales que

f(alpha v) = overline{alpha}f(v).

Inyección en el doble-dual

Hay un homomorfismo natural $Psi$ desde $V$ en el doble dual ${displaystyle V^{**}={Phi:V^{*}to F:Phi mathrm {linear} }}$ , definida por ${displaystyle (Psi (v))(varphi)=varphi (v)}$ para todos ${displaystyle vin V,varphi in V^{*}}$ . En otras palabras, si ${displaystyle mathrm {ev} _{v}:V^{*}to F}$ es el mapa de evaluación definido por ${displaystyle varphi mapsto varphi (v)}$ , entonces ${displaystyle Psi:Vto V^{**}}$ se define como el mapa ${displaystyle vmapsto mathrm {ev} _{v}}$ . Este mapa $Psi$ es siempre inyectable; es un isomorfismo si y sólo si $V$ es finito-dimensional. De hecho, el isomorfismo de un espacio vectorial de dimensiones finitas con su doble dual es un ejemplo arquetípico de un isomorfismo natural. Infinito-dimensional Los espacios de Hilbert no son isomorfos a sus dobles algebraicos, sino a sus dobles continuos.

Transposición de un mapa lineal

Si $f : V \to W$ es un mapa lineal, entonces el transponer (o dual) $f * : W * \to V *$ está definido por

f^*(varphi) = varphi circ f ,

para todos ${displaystyle varphi in W^{*}}$ . El resultado funcional ${displaystyle f^{*}(varphi)}$ dentro $V^{*}$ se llama Retirada de $varphi$ y $f$ .

La siguiente identidad tiene para todos ${displaystyle varphi in W^{*}}$ y $vin V$ :

[f^*(varphi),, v] = [varphi,, f(v)],

donde el paréntesis [·,·] de la izquierda es el emparejamiento natural de V con su doble espacio, y el de la derecha es el emparejamiento natural de W con su doble. Esta identidad caracteriza la transposición y es formalmente similar a la definición del adjunto.

La asignación $f \mapsto f *$ produce un mapa lineal inyectivo entre el espacio de operadores lineales de V a W y el espacio de operadores lineales de W ^∗ a V^∗; este homomorfismo es un isomorfismo si y solo si W es de dimensión finita. Si $V = W$ entonces el espacio de mapas lineales es en realidad un álgebra bajo composición de mapas, y la asignación es entonces un antihomomorfismo de álgebras, lo que significa que $(fg) * = g * f * . En el lenguaje de la teoría de categorías, tomar el dual de espacios vectoriales y la transposición de aplicaciones lineales es, por lo tanto, un funtor contravariante de la categoría de espacios vectoriales sobre F a sí misma. Es posible identificar (f *) * con f utilizando la inyección natural en el doble dual.$

Si el mapa lineal f está representado por la matriz A con respecto a dos bases de V y W, entonces f^∗ está representado por la matriz transpuesta A^T con respecto a las bases duales de W^∗ y V^∗, de ahí el nombre. Alternativamente, como f está representado por A actuando a la izquierda en los vectores de columna, f^∗ está representado por la misma matriz que actúa a la derecha sobre los vectores fila. Estos puntos de vista están relacionados por el producto interno canónico en Rⁿ, que identifica el espacio de vectores columna con el espacio dual de vectores fila.

Espacios cocientes y aniquiladores

Sea S un subconjunto de V. El aniquilador de S en V^∗, denotado aquí S⁰, es la colección de funcionales lineales $f \in V *$ tal que $[f, s] = 0$ para todos los $s \in S$ . Es decir, S⁰ consta de todos los funcionales lineales $f : V \to F$ tal que la restricción a S desaparece: $f | S = 0$ . Dentro de espacios vectoriales de dimensión finita, el aniquilador es dual (isomorfo) al complemento ortogonal.

El aniquilador de un subconjunto es en sí mismo un espacio vectorial. El aniquilador del vector cero es todo el espacio dual: ${displaystyle {0}^{0}=V^{*}}$ , y el aniquilador de todo el espacio es sólo el covector cero: ${displaystyle V^{0}={0}subseteq V^{*}}$ . Además, la asignación de un aniquilador a un subconjunto de V revierte las inclusiones, así que si $S \subseteq T \subseteq V$ , entonces

{displaystyle 0subseteq T^{0}subseteq S^{0}subseteq V^{*}.}

Si A y B son dos subconjuntos de V entonces

{displaystyle A^{0}+B^{0}subseteq (Acap B)^{0},}

y la igualdad se mantiene siempre que V sea de dimensión finita. Si A_i es cualquier familia de subconjuntos de V indexados por i pertenecientes a algún conjunto de índices I , entonces

{displaystyle left(bigcup _{iin I}A_{i}right)^{0}=bigcap _{iin I}A_{i}^{0}.}

En particular, si A y B son subespacios de V entonces

{displaystyle (A+B)^{0}=A^{0}cap B^{0}.}

Si V es de dimensión finita y W es un subespacio vectorial, entonces

{displaystyle W^{00}=W}

después de identificar W con su imagen en el segundo espacio dual bajo el isomorfismo de doble dualidad $V \approx V **$ . En particular, formar el aniquilador es una conexión de Galois en la red de subconjuntos de un espacio vectorial de dimensión finita.

Si W es un subespacio de V entonces el espacio cociente V/W es un espacio vectorial en por derecho propio, y también lo tiene un dual. Por el primer teorema de isomorfismo, un funcional $f : V \to F$ factores a través de V/W si y solo si W está en el kernel de f. Por lo tanto, hay un isomorfismo

{displaystyle (V/W)^{*}cong W^{0}.}

Como consecuencia particular, si V es una suma directa de dos subespacios A y B, entonces V^∗ es una suma directa de A⁰ y B⁰.

Análisis dimensional

El espacio dual es análogo a un espacio "negativo". Simplemente, desde un vector $vin V$ se puede emparejar con un covector $varphi in V^{*}$ por el apareamiento natural ${displaystyle langle x,varphi rangle:=varphi (x)in F}$ para obtener un escalar, un covector puede "cancel" la dimensión de un vector, similar a reducir una fracción. Así, mientras que la suma directa ${displaystyle Voplus V^{*}}$ es un $2n$ - espacio dimensional (si $V$ es $n$ -dimensional), $V^{*}$ se comporta como un ${displaystyle (-n)}$ - espacio dimensional, en el sentido de que sus dimensiones pueden ser canceladas contra las dimensiones de $V$ . Esto es formalizado por la contracción tensor.

Esto surge en la física a través del análisis dimensional, donde el espacio dual tiene unidades inversas. Bajo el acoplamiento natural, estas unidades cancelan, y el valor de escalar resultante es indimensional, como se esperaba. Por ejemplo en (continua) Análisis de Fourier, o más amplio análisis de frecuencia-tiempo: dado un espacio vectorial unidimensional con una unidad de tiempo $t$ , el espacio dual tiene unidades de frecuencia: ocurrencias per unidad de tiempo (unidades de $1/t$ ). Por ejemplo, si el tiempo se mide en segundos, la unidad dual correspondiente es la segunda inversa: a lo largo de 3 segundos, un evento que ocurre 2 veces por segundo ocurre un total de 6 veces, correspondiente a ${displaystyle 3scdot 2s^{-1}=6}$ . Del mismo modo, si el espacio primario mide longitud, el espacio dual mide longitud inversa.

Espacio dual continuo

Al tratar con espacios vectoriales topológicos, las funciones lineales continuas del espacio en el campo base ${displaystyle mathbb {F} =mathbb {C} }$ (o $mathbb {R}$ ) son particularmente importantes. Esto da lugar a la noción del "espacio dual continuo" o " dual topológico" que es un subespacio lineal del espacio dual algebraico $V^{*}$ , denotado por $V'$ . Para cualquier finito-dimensional nimado espacio vectorial o espacio vectorial topológico, como Euclidean n-espacio, el dual continuo y el dual algebraico coinciden. Esto es, sin embargo, falso para cualquier espacio infinito, como lo demuestra el ejemplo de mapas lineales discontinuas. Sin embargo, en la teoría de los espacios vectoriales topológicos los términos "espacio dual continuo" y "espacio dual totopológico" a menudo son reemplazados por "espacio dual".

Para un espacio vectorial topológico $V$ su espacio dual continuo, o espacio dual topológico, o simplemente espacio dual (en el sentido de la teoría de los espacios vectoriales topológicos) $V'$ se define como el espacio de todas las funciones lineales continuas $varphi:Vto{mathbb F}$ .

Ejemplos importantes para espacios duales continuos son el espacio de funciones de prueba compatibles compactamente ${mathcal {D}}$ y su doble ${displaystyle {mathcal {D}}',}$ el espacio de las distribuciones arbitrarias (funciones generalizadas); el espacio de las funciones de prueba arbitraria ${mathcal {E}}$ y su doble ${displaystyle {mathcal {E}}',}$ el espacio de distribuciones compatibles compactamente; y el espacio de reducción rápida de las funciones de prueba ${displaystyle {mathcal {S}},}$ el espacio Schwartz, y su doble ${displaystyle {mathcal {S}}',}$ el espacio de distribuciones templadas (distribuciones de crecimiento lento) en la teoría de las funciones generalizadas.

Propiedades

Si $X$ es un espacio vectorial topológico de Hausdorff (TVS), entonces el espacio dual continuo de $X$ es idéntico al espacio dual continuo de la finalización de $X.$

Topologías en el dual

Hay una construcción estándar para introducir una topología en el dual continuo $V'$ de un espacio vectorial topológico $V$ . Fijar una colección ${mathcal {A}}$ of bounded subsets of $V$ . Esto da la topología en $V$ de convergencia uniforme en conjuntos ${displaystyle {mathcal {A}},}$ o lo que es lo mismo, la topología generada por seminormas de la forma

{displaystyle |varphi |_{A}=sup _{xin A}|varphi (x)|,}

Donde $varphi$ es un funcionamiento lineal continuo en $V$ , y $A$ corre sobre la clase ${displaystyle {mathcal {A}}.}$

Esto significa que una red de funcionalidades $varphi _{i}$ tiende a un funcional $varphi$ dentro $V'$ si

{displaystyle {text{ for all }}Ain {mathcal {A}}qquad |varphi _{i}-varphi |_{A}=sup _{xin A}|varphi _{i}(x)-varphi (x)|{underset {ito infty }{longrightarrow }}0.}

Generalmente (pero no necesariamente) la clase ${mathcal {A}}$ se supone que debe satisfacer las siguientes condiciones:

Cada punto $x$ de $V$ pertenece a algún juego $Ain {mathcal {A}}$ :

{displaystyle {text{ for all }}xin Vquad {text{ there exists some }}Ain {mathcal {A}}quad {text{ such that }}xin A.}

Cada dos sets $Ain {mathcal {A}}$ y ${displaystyle Bin {mathcal {A}}}$ están contenidos en algunos conjuntos ${displaystyle Cin {mathcal {A}}}$ :

{displaystyle {text{ for all }}A,Bin {mathcal {A}}quad {text{ there exists some }}Cin {mathcal {A}}quad {text{ such that }}Acup Bsubseteq C.}

${mathcal {A}}$ se cierra bajo el funcionamiento de la multiplicación por los escalares:

{displaystyle {text{ for all }}Ain {mathcal {A}}quad {text{ and all }}lambda in {mathbb {F} }quad {text{ such that }}lambda cdot Ain {mathcal {A}}.}

Si estos requisitos se cumplen entonces la topología correspondiente en $V'$ es Hausdorff y los sets

<math alttext="{displaystyle U_{A}~=~left{varphi in V'~:~quad |varphi |_{A}UA={}φ φ ▪ ▪ V.:.. φ φ .. A.1},paraA▪ ▪ A{displaystyle U_{A}~=~left{varphi in V'~quad "Sobrevivirvarphi {fnfnfnh}Ain {fn}in {fnh}<img alt="{displaystyle U_{A}~=~left{varphi in V'~:~quad |varphi |_{A}

formar su base local.

Estos son los tres casos especiales más importantes.

La fuerte topología en $V'$ es la topología de la convergencia uniforme en subconjuntos atados en $V$ (también aquí ${mathcal {A}}$ puede ser elegido como la clase de todos los subconjuntos atados en $V$ ).

Si $V$ es un espacio vectorial normal (por ejemplo, un espacio de Banach o un espacio de Hilbert) entonces la fuerte topología en $V'$ es ordenado (de hecho un espacio de Banach si el campo de los escalares es completo), con la norma

{displaystyle |varphi |=sup _{|x|leq 1}|varphi (x)|.}

La topología estereotipada en $V'$ es la topología de la convergencia uniforme en conjuntos totalmente ligados en $V$ (también aquí ${mathcal {A}}$ puede ser elegido como la clase de todos los subconjuntos totalmente atados en $V$ ).
La débil topología en $V'$ es la topología de la convergencia uniforme en subconjuntos finitos en $V$ (también aquí ${mathcal {A}}$ puede ser elegido como la clase de todos los subconjuntos finitos en $V$ ).

Cada una de estas tres opciones de topología $V'$ conduce a una variante de la propiedad de la reflexividad para los espacios vectoriales topológicos:

Si $V'$ está dotado con la fuerte topología, entonces la noción correspondiente de la reflexividad es la estándar: los espacios reflexivos en este sentido se llaman simplemente reflexivo.
Si $V'$ está dotado con la topología dual estereotipo, entonces la reflexividad correspondiente se presenta en la teoría de espacios estereotipados: los espacios reflexivos en este sentido se llaman estereotipo.
Si $V'$ está dotada de la topología débil, entonces la reflexividad correspondiente se presenta en la teoría de pares duales: los espacios reflexivos en este sentido son espacios arbitrarios (Hausdorff) localmente convexos con la topología débil.

Ejemplos

Sea 1 < p < ∞ sea un número real y considere el espacio de Banach ℓ p de todas las sucesiones $a = (a <sub n)$ para el cual

<math alttext="{displaystyle |mathbf {a} |_{p}=left(sum _{n=0}^{infty }|a_{n}|^{p}right)^{frac {1}{p}}.. a.. p=().. n=0JUEGO JUEGO SilencioanSilenciop)1p.JUEGO JUEGO .{displaystylefnMitbf} "Perfecto" ¿Qué? ¿Por qué? - No.<img alt="{displaystyle |mathbf {a} |_{p}=left(sum _{n=0}^{infty }|a_{n}|^{p}right)^{frac {1}{p}}

Define el número q por $1/ p + 1/ q = 1$ . Luego el dual continuo l^p se identifica naturalmente con l^q: dado un elemento ${displaystyle varphi in (ell ^{p})'}$ , el elemento correspondiente $l q$ es la secuencia ${displaystyle (varphi (mathbf {e} _{n}))}$ Donde ${displaystyle mathbf {e} _{n}}$ denota la secuencia cuyo $n$ - es 1 y todos los demás son cero. Por el contrario, dado un elemento $a = a n) l q$ , el funcional lineal continuo correspondiente $varphi$ on $l p$ se define por

{displaystyle varphi (mathbf {b})=sum _{n}a_{n}b_{n}}

para todos $b = (b n) \in ℓ p$ (ver desigualdad de Hölder).

De manera similar, el dual continuo de $ℓ 1$ se identifica naturalmente con $ℓ \infty$ (el espacio de secuencias acotadas). Además, los duales continuos de los espacios de Banach c (que consisten en todas las sucesiones convergentes, con la norma suprema) y c₀ (las sucesiones convergentes a cero) se identifican naturalmente con $ℓ 1$ .

Según el teorema de representación de Riesz, el dual continuo de un espacio de Hilbert es nuevamente un espacio de Hilbert que es antiisomorfo al espacio original. Esto da lugar a la notación bra-ket utilizada por los físicos en la formulación matemática de la mecánica cuántica.

Según el teorema de representación de Riesz-Markov-Kakutani, el dual continuo de ciertos espacios de funciones continuas se puede describir usando medidas.

Transposición de un mapa lineal continuo

Si $T : V \to W$ es un mapa lineal continuo entre dos espacios vectoriales topológicos, entonces el (continuo) transponer $T' : W' \to V'$ se define con la misma fórmula que antes:

{displaystyle T'(varphi)=varphi circ T,quad varphi in W'.}

La $T' (φ)$ funcional resultante está en $V'$ . La asignación $T \to T'$ produce un mapa lineal entre el espacio de mapas lineales continuos de V a W y el espacio de mapas lineales desde $W'$ hasta $V'$ . Cuando T y U son mapas lineales continuos componibles, entonces

{displaystyle (Ucirc T)'=T'circ U'.}

Cuando V y W son espacios normados, la norma de la transposición en $L (W', V')$ es igual a T en $L (V, W)$ . Varias propiedades de la transposición dependen del teorema de Hahn-Banach. Por ejemplo, el mapa lineal acotado T tiene un rango denso si y solo si la transposición $T'$ es inyectiva.

Cuando T es un mapa lineal compacto entre dos espacios de Banach V y W, entonces la transposición $T'$ es compacto. Esto se puede probar usando el teorema de Arzelà-Ascoli.

Cuando V es un espacio de Hilbert, existe un isomorfismo antilineal i_V de V a su continua doble $V'$ . Para cada mapa lineal acotado T en V, los operadores transpuesto y adjunto están vinculados por

{displaystyle i_{V}circ T^{*}=T'circ i_{V}.}

Cuando T es un mapa lineal continuo entre dos espacios vectoriales topológicos V y W, entonces la transposición <span class="texhtml" T′ es continuo cuando $W'$ y $V'$ están equipados con "compatible" topologías: por ejemplo, cuando para $X = V$ y $X = W$ , ambos duales $X'$ tienen la topología fuerte $β (X', X)$ de convergencia uniforme en conjuntos acotados de X, o ambos tienen la topología débil-* $σ (X', X)$ de pointwise convergencia en X. La transposición $T'$ es continua desde $β (W', W)$ a $β (V', V)$ , o desde $σ (W', W)$ a $σ (V', V)$ .

Aniquiladores

Suponga que W es un subespacio lineal cerrado de un espacio normado V y considere el aniquilador de W en $V'$ ,

{displaystyle W^{perp }={varphi in V':Wsubseteq ker varphi }.}

Entonces, el dual del cociente $V / W$ se puede identificar con W^⊥, y el dual de W se puede identificar con el cociente $V' / W ⊥$ . De hecho, sea P la sobreyección canónica de V sobre el cociente $V / W$ ; entonces, la transpuesta $P'$ es un isomorfismo isométrico de $(V / W)'$ en $V'$ , con rango igual a W^⊥. Si j denota el mapa de inyección de W a V, entonces el núcleo de la transposición $j '$ es el aniquilador de W:

ker (j') = W^perp

y se deduce del teorema de Hahn-Banach que $j'$ induce un isomorfismo isométrico $V' / W ⊥ \to W'$ .

Otras propiedades

Si el dual de un espacio normado $V$ es separable, entonces también lo es el espacio $V$ en sí mismo. Lo contrario no es cierto: por ejemplo, el espacio $ℓ 1$ es separable, pero su doble $ℓ \infty$ no lo es.

Doble doble

Esta es una transformación natural de la adición vectorial de un espacio vectorial a su doble dual.

. x 1, x 2 .

denota el par ordenado de dos vectores. La adición + envía x₁ y x₂ a

x 1 + x 2

. La adición +′ inducida por la transformación puede definirse como ${displaystyle [Psi (x_{1})+'Psi (x_{2})](varphi)=varphi (x_{1}+x_{2})=varphi (x)}$ para cualquier $varphi$ en el espacio dual.

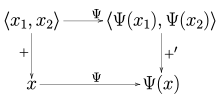
En analogía con el caso del doble dual algebraico, siempre hay un operador lineal continuo naturalmente definido $Ψ: V \to V''$ de un espacio normado V a su continuo doble dual $V''$ , definido por

{displaystyle Psi (x)(varphi)=varphi (x),quad xin V, varphi in V'.}

Como consecuencia del teorema de Hahn-Banach, este mapa es de hecho una isometría, lo que significa $‖ Ψ(x) ‖ = ‖ x ‖$ para todos los $x \in V$ . Los espacios normados para los que la función Ψ es una biyección se denominan reflexivos.

Cuando V es un espacio vectorial topológico, entonces Ψ(x) todavía se puede definir con la misma fórmula, para cada $x \in V$ , sin embargo surgen varias dificultades. Primero, cuando V no es localmente convexo, el dual continuo puede ser igual a { 0 } y el mapa Ψ trivial. Sin embargo, si V es Hausdorff y localmente convexa, la función Ψ es inyectiva de V al dual algebraico $V' *$ del dual continuo, de nuevo como consecuencia del teorema de Hahn-Banach.

En segundo lugar, incluso en la configuración localmente convexa, se pueden definir varias topologías de espacio vectorial natural en la $V'$ dual continua, de modo que la continua double dual $V''$ no se define de forma única como un conjunto. Decir que Ψ se asigna de V a $V''$ , o en otras palabras, que Ψ(x) es continua en $V'$ para cada $x \in V$ , es un requisito mínimo razonable en la topología de $V'$ , es decir, que las asignaciones de evaluación

{displaystyle varphi in V'mapsto varphi (x),quad xin V,}

ser continuo para la topología elegida en $V'$ . Además, todavía existe la posibilidad de elegir una topología en $V''$ , y la continuidad de Ψ depende de esta elección. Como consecuencia, definir la reflexividad en este marco es más complicado que en el caso normado.

Contenido relacionado

Más resultados...