Dodecágono

En geometría, un dodecágono, o 12 góndos, es cualquier polígono de doce lados.

Dodecágono regular

Un dodecágono regular es una figura con lados de la misma longitud y ángulos internos del mismo tamaño. Tiene doce ejes de simetría reflexiva y simetría rotacional de orden 12. Un dodecágono regular está representado por el símbolo de Schläfli {12} y puede construirse como un hexágono truncado, t{6}, o un triángulo dos veces truncado, tt{3 }. El ángulo interno en cada vértice de un dodecágono regular es de 150°.

Área

El área de un dodecágono regular de longitud de lado a viene dada por:

${fnMicroc {pi}derecha)a^{2}=3left(2+{sqrt {3}right)a^{2}=3sqrt {3}right)a^{2}simeq 11.19615242,a^{2}end{aligned}}} {f}}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn$

Y en términos de la apotema r (ver también la figura inscrita), el área es:

${fnMicroc {pi}right)r^{2}=12left(2-{sqrt {3}right)r^{2}=12left(2-{sqrt {3}right)r^{2}\\simeq 3.2153903,r^{2}end{aligned}}}}}}}}}}$

En términos del circunradio R, el área es:

${displaystyle A=6sin left({frac {pi - Sí.$

El lapso S del dodecágono es la distancia entre dos lados paralelos y es igual al doble de la apotema. Una fórmula simple para el área (dada la longitud del lado y la luz) es:

${displaystyle A=3aS}$

Esto se puede verificar con la relación trigonométrica:

${displaystyle S=a(1+2cos {30^{circ }}+2cos {60^{circ }}}}$

Perímetro

El perímetro de un dodecágono regular en términos de circunradio es:

${displaystyle {begin{aligned}p limit=24Rtan left({frac {pi }{12}}right)=12R{sqrt {2-{sqrt {3}}\\simeq 6.21165708246,Rend{aligned}}}$

El perímetro en términos de apotema es:

${displaystyle {begin{aligned}p limit=24rtan left({frac {pi }{12}}right)=24r(2-{sqrt {3})\\simeq 6.43078061835,rend{aligned}}}}}}}}}}}$

Este coeficiente es el doble del coeficiente encontrado en la ecuación de la apotema para el área.

Construcción del dodecágono

Como 12 = 2² × 3, el dodecágono regular se puede construir usando la construcción con compás y regla:

Construcción de un dodecagón regular en un círculo dado

Construcción de un dodecagon regular
a un lado dado, animación. (La construcción es muy similar a la del octógono a una longitud parcial determinada.)

Disección

12-cube	60 romb disección

Coxeter afirma que cada zonogon (un 2m-gon cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en m(m-1)/2 paralelogramos. En particular, esto es cierto para los polígonos regulares con el mismo número de lados, en cuyo caso todos los paralelogramos son rombos. Para el dodecágono regular, m=6, y se puede dividir en 15: 3 cuadrados, 6 rombos anchos de 30° y 6 rombos estrechos de 15°. Esta descomposición se basa en una proyección del polígono de Petrie de un cubo de 6, con 15 de 240 caras. La secuencia OEIS A006245 define el número de soluciones como 908, incluidas rotaciones de hasta 12 veces y formas quirales en reflexión.

Disección en 15 rombs

6-cube

Una de las formas en que se utilizan los bloques de patrones de manipulación matemática es para crear varios dodecágonos diferentes. Están relacionadas con las disecciones rómbicas, con 3 rombos de 60° fusionados en hexágonos, trapecios de medio hexágono o divididos en 2 triángulos equiláteros.

Otras disecciones regulares

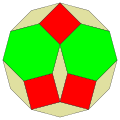Azulejos socolares

Bloques de patrón

Simetría

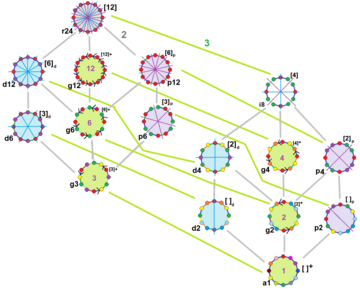
El dodecágono regular tiene simetría Dih₁₂, orden 24. Hay 15 simetrías diédricas y cíclicas de subgrupos distintos. Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Sólo el subgrupo g12 no tiene grados de libertad pero puede verse como aristas dirigidas.

Ejemplo de dodecagones por simetría
r24
d12	g12	p12		i8
d6	g6	p6		d4	g4	p4
g3				d2	g2	p2
a1

Ocurrencia

Mosaico

Un dodecágono regular puede llenar un vértice plano con otros polígonos regulares de 4 maneras:

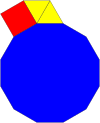3.12.12	4.6.12	3.3.4.12	3.4.3.12

Aquí hay 3 ejemplos de mosaicos de planos periódicos que utilizan dodecágonos regulares, definidos por su configuración de vértice:

1-uniform		2-uniform
3.12.12	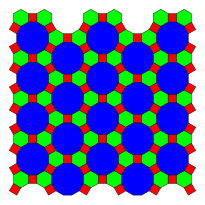4.6.12	3.12.12; 3.4.3.12

Dodecágono sesgado

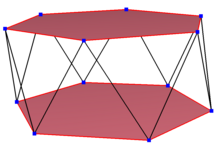
Un dodecágono sesgado es un polígono sesgado con 12 vértices y aristas pero que no existe en el mismo plano. El interior de tal dodecágono generalmente no está definido. Un dodecágono en zigzag sesgado tiene vértices que se alternan entre dos planos paralelos.

Un dodecágono sesgado regular es transitivo por vértices con longitudes de aristas iguales. En 3 dimensiones será un dodecágono oblicuo en zig-zag y se podrá ver en los vértices y aristas laterales de un antiprisma hexagonal con el mismo D_5d, [2⁺,10] simetría, orden 20. El antiprisma dodecagrámico, s{2,24/5} y el antiprisma cruzado dodecagrámico, s{2,24/7} también tienen dodecágonos sesgados regulares.

Polígonos de Petrie

El dodecágono regular es el polígono de Petrie para muchos politopos de dimensiones superiores, visto como proyecciones ortogonales en planos de Coxeter. Ejemplos en 4 dimensiones son el duoprisma de 24 celdas, el de 24 celdas chato, el duoprisma de 6-6 y la duopirámide de 6-6. En 6 dimensiones, 6 cubos, 6 ortoplex, 221, 122. También es el polígono de Petrie para el gran 120 celdas y el gran estrellado de 120 celdas.

Dodecagones skew regulares en dimensiones superiores
E6		F4		2G2 (4D)
221	122	24 horas	Snub 24-cell	6-6 duopyramid	{6}×{6}
A11	D7		B6		4A2
11-simplex	(411)	141	6-orthoplex	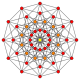6-cube	{3}×{3}×{3}

Cifras relacionadas

Un dodecagrama es un polígono estrella de 12 lados, representado por el símbolo {12/n}. Hay un polígono de estrella regular: {12/5}, que usa los mismos vértices, pero conecta cada cinco puntos. También hay tres compuestos: {12/2} se reduce a 2{6} como dos hexágonos, y {12/3} se reduce a 3{4} como tres cuadrados, {12/4} se reduce a 4{3 } como cuatro triángulos, y {12/6} se reduce a 6{2} como seis digones degenerados.

Estrellas y compuestos
n	1	2	3	4	5	6
Formulario	Polygon	Compuestos			Pológono estrella	Compuesto
Imagen	{12/1} = {12}	{12/2} o 2{6}	{12/3} o 3{4}	{12/4} o 4{3}	{12/5}	{12/6} o 6{2}

Los truncamientos más profundos del dodecágono y los dodecagramas regulares pueden producir formas poligonales de estrella intermedias isogonales (transitivas a vértices) con vértices espaciados iguales y dos longitudes de aristas. Un hexágono truncado es un dodecágono, t{6}={12}. Un hexágono cuasitruncado, invertido como {6/5}, es un dodecagrama: t{6/5}={12/5}.

truncaciones verticales-transitivas del hexágono
Quasiregular	Isogonal		Quasiregular
t{6}={12}			t{6/5}={12/5}

Ejemplos en uso

En mayúsculas, las letras E, H y X (y I en una fuente slab serif) tienen contornos dodecagonales. Una cruz es un dodecágono, al igual que el logotipo de la división de automóviles Chevrolet.

El dodecágono regular ocupa un lugar destacado en muchos edificios. La Torre del Oro es una torre de vigilancia militar dodecagonal en Sevilla, sur de España, construida por la dinastía almohade. La iglesia de la Vera Cruz de principios del siglo XIII en Segovia, España, es dodecagonal. Otro ejemplo es la Porta di Venere (Puerta de Venus), en Spello, Italia, construida en el siglo I a.C. y tiene dos torres dodecagonales, llamadas "Propertius' Torres".

Las monedas dodecagonales regulares incluyen:

• Trío británico de 1937 a 1971, cuando dejó de ser legal.
• British One Pound Coin, presentado en 2017.
• Moneda de 50 centavos australianos
• Fiji 50 centavos
• Tongan 50-seniti, since 1974
• Islas Salomón 50 centavos
• Croata 25 kuna
• Rumania 5000 lei, 2001–2005
• Dinero canadiense, 1982 a 1996
• Vietnamita del Sur 20 đ rechazang, 1968-1975
• Zambian 50 ngwee, 1969–1992
• Malawian 50 tambala, 1986–1995
• México 20 centavos, 1992-2009