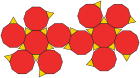
Dodecaedro truncado

Truncado dodecaedro
(Haga clic aquí para el modelo giratorio)
Tipo	Arquitecto sólido Uniform polyhedron
Elementos	F = 32, E = 90, V = 60 (χ = 2)
Caras por lados	20{3}+12{10}
Notación de Conway	tD
Símbolos de Schläfli	t{5,3}
	t0,1{5,3}
Signatura Wythoff	2 3 Silencio 5
Coxeter diagrama
Grupo de Symmetry	Ih, H3, [5,3], (*532), orden 120
Grupo de rotación	I, [5,3]+, (532), orden 60
Ángulo Dihedral	10-10: 116,57° 3-10: 142,62°
Referencias	U26, C29, W10
Propiedades	Convex semiregular
Caras de colores	3.10.10 (Vertex figure)
Triakis icosahedron (poliedro dual)	Cifras netas

En geometría, el dodecaedro truncado es un sólido de Arquímedes. Tiene 12 caras decagonales regulares, 20 caras triangulares regulares, 60 vértices y 90 aristas.

Relaciones geométricas

Este poliedro se puede formar a partir de un dodecaedro regular truncando (cortando) las esquinas de modo que las caras del pentágono se conviertan en decágonos y las esquinas en triángulos.

Se utiliza en el teselado de relleno de espacio hiperbólico transitivo de células, el panal icosaédrico bitruncado.

Área y volumen

El área A y el volumen V de un dodecaedro truncado de longitud de arista a son:

A=5()3+65+25)a2.. 100.99076a2V=512()99+475)a3.. 85.0396646a3{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicros} {fnMicrosoft Sans Serif} {fnMicros} {fnMicros}}} {f}}}}} {f}}}}} {f}}}f}f}}f}fnMicrom}f}}f}fnMicrostítuotrosssssssssstítulorando,f}fnun}fnMinMissssssssssssssssssssssssssssss}f}fnun}fnMinMissssssssssssssssssssssss

Coordenadas cartesianas

Las coordenadas cartesianas de los vértices de un dodecaedro truncado con una longitud de arista 2φ − 2, centradas en el origen, son todas permutaciones pares de:

(0, ±1/φ±(2 +φ)

(±1/φ±φ±2φ)

(±φ± 2, ±φ+ 1))

donde φ = 1 + √5/2 es la proporción áurea.

Proyecciones ortogonales

El dodecaedro truncado tiene cinco proyecciones ortogonales especiales, centradas: en un vértice, en dos tipos de aristas y en dos tipos de caras. Los dos últimos corresponden a los planos A₂ y H₂ de Coxeter.

Proyecciones ortogonales

Centrado por	Vertex	Edge 3-3	Edge 10-10	Cara Triángulo	Cara Decagon
Sólido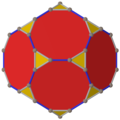
Wireframe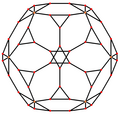
Projective simetría	[2]	[2]	[2]	[6]	[10]
Doble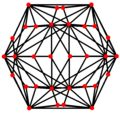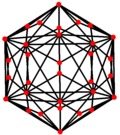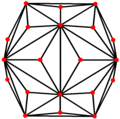

Mosaicos esféricos y diagramas de Schlegel

El dodecaedro truncado también se puede representar como un mosaico esférico y proyectarse en el plano mediante una proyección estereográfica. Esta proyección es conforme y conserva los ángulos pero no las áreas ni las longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Los diagramas de Schlegel son similares, con una proyección en perspectiva y bordes rectos.

Proyección ortográfica	Proyecciones estereográficas
	Decagon-centered	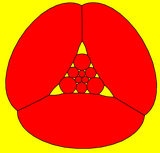Triángulo centrado

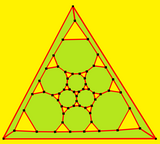Disposición de vértices

Comparte su disposición de vértices con tres poliedros uniformes no convexos:

Truncado dodecaedro

Great icosidodecahedron

Gran ditrigonal dodecicosidodecahedron

Great dodecicosahedron

Poliedros y mosaicos relacionados

Es parte de un proceso de truncamiento entre un dodecaedro y un icosaedro:

Family of uniform icosahedral polyhedra
Simetría: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros truncados uniformes con configuraciones de vértice (3.2n.2n), y [n,3] Simetría del grupo Coxeter.

*n32 mutación simetría de los revestimientos esféricos truncados: t{n,3}
Simmetría *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Truncado cifras
Signatura	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	.
Triakis cifras
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3. Testamento.

Gráfico dodecaédrico truncado

En el campo matemático de la teoría de grafos, un gráfico dodecaédrico truncado es el gráfico de vértices y aristas del dodecaedro truncado, uno de los sólidos de Arquímedes. Tiene 60 vértices y 90 aristas, y es un gráfico de Arquímedes cúbico.

Circular