Divergencia

ImprimirCitar

Operador vectorial que mide la expansión o salida de un campo vectorial

La divergencia de diferentes campos vectoriales. La divergencia de vectores desde el punto (x, y) equivale a la suma del derivado parcial con respeto a x del x-componente y el derivado parcial con respeto al y-componente en ese punto:

{displaystyle nabla !cdot (mathbf {V} (x,y))={frac {partial {V_{x}(x,y)}}{partial {x}}}+{frac {partial {V_{y}(x,y)}}{partial {y}}}}

En cálculo vectorial, divergencia es un operador vectorial que opera en un campo vectorial, produciendo un campo escalar que proporciona la cantidad de la fuente del campo vectorial en cada punto. Más técnicamente, la divergencia representa la densidad de volumen del flujo hacia afuera de un campo vectorial desde un volumen infinitesimal alrededor de un punto dado.

Como ejemplo, considere el aire mientras se calienta o se enfría. La velocidad del aire en cada punto define un campo vectorial. Mientras que el aire se calienta en una región, se expande en todas las direcciones y, por lo tanto, el campo de velocidad apunta hacia afuera de esa región. La divergencia del campo de velocidades en esa región tendría entonces un valor positivo. Mientras el aire se enfría y por lo tanto se contrae, la divergencia de la velocidad tiene un valor negativo.

Interpretación física de la divergencia

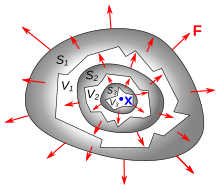
En términos físicos, la divergencia de un campo vectorial es la medida en que el flujo del campo vectorial se comporta como una fuente en un punto determinado. Es una medida local de su "extroversión" – la medida en que hay más vectores de campo saliendo de una región infinitesimal del espacio que entrando en ella. Un punto en el que el flujo sale tiene una divergencia positiva y, a menudo, se denomina "fuente" en el campo. Un punto en el que el flujo se dirige hacia el interior tiene una divergencia negativa y, a menudo, se denomina "sumidero" en el campo. Cuanto mayor sea el flujo de campo a través de una pequeña superficie que encierra un punto dado, mayor será el valor de la divergencia en ese punto. Un punto en el que hay cero flujo a través de una superficie envolvente tiene cero divergencia.

La divergencia de un campo vectorial a menudo se ilustra utilizando el ejemplo simple del campo de velocidad de un fluido, un líquido o un gas. Un gas en movimiento tiene una velocidad, una rapidez y una dirección en cada punto, que se pueden representar mediante un vector, por lo que la velocidad del gas forma un campo vectorial. Si se calienta un gas, se expandirá. Esto provocará un movimiento neto de partículas de gas hacia el exterior en todas las direcciones. Cualquier superficie cerrada en el gas encerrará el gas que se está expandiendo, por lo que habrá un flujo de gas hacia el exterior a través de la superficie. Entonces, el campo de velocidad tendrá divergencia positiva en todas partes. De manera similar, si el gas se enfría, se contraerá. Habrá más espacio para partículas de gas en cualquier volumen, por lo que la presión externa del fluido provocará un flujo neto de volumen de gas hacia el interior a través de cualquier superficie cerrada. Por lo tanto, el campo de velocidad tiene divergencia negativa en todas partes. Por el contrario, en un gas a temperatura y presión constantes, el flujo neto de gas que sale de cualquier superficie cerrada es cero. El gas puede estar en movimiento, pero la tasa de volumen del gas que fluye hacia cualquier superficie cerrada debe ser igual a la tasa de volumen que sale, por lo que el flujo neto es cero. Por lo tanto, la velocidad del gas tiene divergencia cero en todas partes. Un campo que tiene divergencia cero en todas partes se llama solenoidal.

Si el gas se calienta solo en un punto o región pequeña, o si se introduce un pequeño tubo que suministra una fuente de gas adicional en un punto, el gas se expandirá, empujando las partículas de fluido a su alrededor hacia afuera en todas las direcciones. Esto provocará un campo de velocidad hacia el exterior en todo el gas, centrado en el punto calentado. Cualquier superficie cerrada que encierre el punto calentado tendrá un flujo de partículas de gas saliendo de ella, por lo que hay una divergencia positiva en ese punto. Sin embargo, cualquier superficie cerrada que no encierre el punto tendrá una densidad constante de gas en el interior, por lo que entran tantas partículas de fluido como salen del volumen, por lo que el flujo neto que sale del volumen es cero. Por lo tanto, la divergencia en cualquier otro punto es cero.

Definición

La divergencia en un momento

x

es el límite de la relación del flujo

Phi

a través de la superficie

S i

(flechas rojas) al volumen

{displaystyle |V_{i}|}

para cualquier secuencia de regiones cerradas

V 1, V 2, V 3,...

enclosing

x

que se aproxima al volumen cero:

{displaystyle operatorname {div} mathbf {F} =lim _{|V_{i}|to 0}{frac {Phi (S_{i})}{|V_{i}|}}}

La divergencia de un campo vectorial $F (x)$ en un punto $x 0$ se define como el límite de la razón de la integral de superficie de $F$ fuera de la superficie cerrada de un volumen $V$ que encierra $x 0$ al volumen de $V$ , como $V$ se reduce a cero

{displaystyle left.operatorname {div} mathbf {F} right|_{mathbf {x_{0}} }=lim _{Vto 0}{frac {1}{|V|}}}

{displaystyle scriptstyle S(V)}

{displaystyle mathbf {F} cdot mathbf {hat {n}} ,dS}

Donde $Silencio V Silencio$ es el volumen de $V$ , $S () V)$ es el límite $V$ , y $mathbf {hat {n}}$ es la unidad externa normal a esa superficie. Se puede demostrar que el límite anterior siempre converge al mismo valor para cualquier secuencia de volúmenes que contengan $x 0$ y enfoque cero volumen. El resultado, $div F$ , es una función de escalar $x$ .

Dado que esta definición no tiene coordenadas, muestra que la divergencia es la misma en cualquier sistema de coordenadas. Sin embargo, no se usa a menudo en la práctica para calcular la divergencia; cuando el campo vectorial se da en un sistema de coordenadas, las definiciones de coordenadas a continuación son mucho más simples de usar.

Un campo vectorial con divergencia cero en todas partes se llama solenoidal, en cuyo caso cualquier superficie cerrada no tiene flujo neto a través de ella.

Definición en coordenadas

Coordenadas cartesianas

En las coordenadas cartesianas tridimensionales, la divergencia de un campo vectorial continuamente diferenciable ${displaystyle mathbf {F} =F_{x}mathbf {i} +F_{y}mathbf {j} +F_{z}mathbf {k} }$ se define como la función de valor escalar:

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} =left({frac {partial }{partial x}},{frac {partial }{partial y}},{frac {partial }{partial z}}right)cdot (F_{x},F_{y},F_{z})={frac {partial F_{x}}{partial x}}+{frac {partial F_{y}}{partial y}}+{frac {partial F_{z}}{partial z}}.}

Aunque se expresa en términos de coordenadas, el resultado es invariable bajo rotaciones, como sugiere la interpretación física. Esto se debe a que la traza de la matriz jacobiana de un campo vectorial $N$ -dimensional $F$ en $N$ -espacio dimensional es invariable bajo cualquier transformación lineal invertible.

La notación común para la divergencia $\nabla \cdot F$ es un mnemotécnico conveniente, donde el punto denota una operación que recuerda al producto escalar: toma el componentes del operador $\nabla$ (ver del), aplicarlos a los componentes correspondientes de $F$ , y suma los resultados. Debido a que aplicar un operador es diferente a multiplicar los componentes, esto se considera un abuso de notación.

Coordenadas cilíndricas

Para un vector expresado en coordenadas cilíndricas unitarias locales como

{displaystyle mathbf {F} =mathbf {e} _{r}F_{r}+mathbf {e} _{theta }F_{theta }+mathbf {e} _{z}F_{z},}

donde $e a$ es el vector unitario en la dirección $a$ , la divergencia es

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} ={frac {1}{r}}{frac {partial }{partial r}}left(rF_{r}right)+{frac {1}{r}}{frac {partial F_{theta }}{partial theta }}+{frac {partial F_{z}}{partial z}}.}

El uso de coordenadas locales es vital para la validez de la expresión. Si lo consideramos $x$ el vector de posición y las funciones $r () x)$ , $Silencio () x)$ , y $z () x)$ , que asigna el correspondiente mundial coordinación cilíndrica a un vector, en general ${displaystyle r(mathbf {F} (mathbf {x}))neq F_{r}(mathbf {x})}$ , ${displaystyle theta (mathbf {F} (mathbf {x}))neq F_{theta }(mathbf {x})}$ , y ${displaystyle z(mathbf {F} (mathbf {x}))neq F_{z}(mathbf {x})}$ . En particular, si consideramos la función de identidad $F () x) x$ , encontramos que:

{displaystyle theta (mathbf {F} (mathbf {x}))=theta neq F_{theta }(mathbf {x})=0}

Coordenadas esféricas

En coordenadas esféricas, con $θ$ el ángulo con el $z$ eje y $φ$ la rotación alrededor del $z$ eje, y $F$ nuevamente escritos en coordenadas de unidades locales, la divergencia es

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} ={frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}F_{r}right)+{frac {1}{rsin theta }}{frac {partial }{partial theta }}(sin theta ,F_{theta })+{frac {1}{rsin theta }}{frac {partial F_{varphi }}{partial varphi }}.}

Campo tensor

Sea $A$ un campo tensorial de segundo orden continuamente diferenciable definido de la siguiente manera:

{displaystyle mathbf {A} ={begin{bmatrix}A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{32}&A_{33}end{bmatrix}}}

la divergencia en el sistema de coordenadas cartesianas es un campo tensorial de primer orden y se puede definir de dos maneras:

{displaystyle operatorname {div} (mathbf {A})={cfrac {partial A_{ik}}{partial x_{k}}}~mathbf {e} _{i}=A_{ik,k}~mathbf {e} _{i}={begin{bmatrix}{dfrac {partial A_{11}}{partial x_{1}}}+{dfrac {partial A_{12}}{partial x_{2}}}+{dfrac {partial A_{13}}{partial x_{3}}}\{dfrac {partial A_{21}}{partial x_{1}}}+{dfrac {partial A_{22}}{partial x_{2}}}+{dfrac {partial A_{23}}{partial x_{3}}}\{dfrac {partial A_{31}}{partial x_{1}}}+{dfrac {partial A_{32}}{partial x_{2}}}+{dfrac {partial A_{33}}{partial x_{3}}}end{bmatrix}}}

{displaystyle nabla cdot mathbf {A} ={cfrac {partial A_{ki}}{partial x_{k}}}~mathbf {e} _{i}=A_{ki,k}~mathbf {e} _{i}={begin{bmatrix}{dfrac {partial A_{11}}{partial x_{1}}}+{dfrac {partial A_{21}}{partial x_{2}}}+{dfrac {partial A_{31}}{partial x_{3}}}\{dfrac {partial A_{12}}{partial x_{1}}}+{dfrac {partial A_{22}}{partial x_{2}}}+{dfrac {partial A_{32}}{partial x_{3}}}\{dfrac {partial A_{13}}{partial x_{1}}}+{dfrac {partial A_{23}}{partial x_{2}}}+{dfrac {partial A_{33}}{partial x_{3}}}\end{bmatrix}}}

Tenemos

{displaystyle operatorname {div} (mathbf {A^{T}})=nabla cdot mathbf {A} }

Si el tensor es simétrico $A ij = A ji$ entonces ${displaystyle operatorname {div} (mathbf {A})=nabla cdot mathbf {A} }$ . Debido a esto, a menudo en la literatura las dos definiciones (y símbolos) $div$ y $nabla cdot$ ) se utilizan intercambiablemente (especialmente en las ecuaciones mecánicas donde se asume la simetría de tensor).

Expresiones de ${displaystyle nabla cdot mathbf {A} }$ en coordenadas cilíndricas y esféricas se dan en el artículo del en coordenadas cilíndricas y esféricas.

Coordenadas generales

Usando la notación de Einstein podemos considerar la divergencia en coordenadas generales, que escribimos como $x 1, \dots, x i, \dots, x n$ , donde $n$ es el número de dimensiones del dominio. Aquí, el índice superior se refiere al número de la coordenada o componente, por lo que $x 2$ se refiere al segundo componente, y no la cantidad $x$ al cuadrado. La variable de índice $i$ se utiliza para hacer referencia a un componente arbitrario, como $x i$ . Entonces, la divergencia se puede escribir mediante la fórmula de Voss-Weyl, como:

{displaystyle operatorname {div} (mathbf {F})={frac {1}{rho }}{frac {partial left(rho ,F^{i}right)}{partial x^{i}}},}

Donde $rho$ es el coeficiente local del elemento de volumen y $F i$ son los componentes ${displaystyle mathbf {F} =F^{i}mathbf {e} _{i}}$ con respecto a los locales no normalizados base covariante (a veces escrita como ${displaystyle mathbf {e} _{i}=partial mathbf {x} /partial x^{i}}$ ). La notación de Einstein implica summation sobre $i$ , ya que aparece como un índice superior e inferior.

El coeficiente de volumen $***$ es una función de posición que depende del sistema de coordenadas. En coordenadas cartesianas, cilíndricas y esféricas, utilizando las mismas convenciones que antes, tenemos $*** = 1$ , $*** = r$ y $*** = r 2 pecado Silencio$ , respectivamente. El volumen también se puede expresar como ${textstyle rho ={sqrt {left|det g_{ab}right|}}}$ , donde $g ab$ es el tensor métrico. El determinante aparece porque proporciona la definición invariante apropiada del volumen, dada un conjunto de vectores. Puesto que el determinante es una cantidad de escalar que no depende de los índices, estos pueden ser suprimidos, escribiendo ${textstyle rho ={sqrt {left|det gright|}}}$ . El valor absoluto se toma para manejar el caso general en el que el determinante podría ser negativo, como en espacios pseudo-riemannianos. La razón de la raíz cuadrada es un poco sutil: Evita eficazmente el doble recuento ya que uno va de las coordenadas curvas a cartesianas, y la espalda. El volumen (el determinante) también se puede entender como el jacobino de la transformación de las coordenadas cartesianas a curvilinear, que para $n = 3$ da ${textstyle rho =left|{frac {partial (x,y,z)}{partial (x^{1},x^{2},x^{3})}}right|}$ .

Algunas convenciones esperan que todos los elementos de base locales se normalicen a la longitud de la unidad, como se hizo en las secciones anteriores. Si escribimos ${hat {mathbf {e} }}_{i}$ para la base normalizada, y ${displaystyle {hat {F}}^{i}}$ para los componentes $F$ con respecto a ella, tenemos que

{displaystyle mathbf {F} =F^{i}mathbf {e} _{i}=F^{i}|{mathbf {e} _{i}}|{frac {mathbf {e} _{i}}{|mathbf {e} _{i}|}}=F^{i}{sqrt {g_{ii}}},{hat {mathbf {e} }}_{i}={hat {F}}^{i}{hat {mathbf {e} }}_{i},}

usando una de las propiedades del tensor métrico. Haciendo ambas caras de la última igualdad con el elemento contravariante ${displaystyle {hat {mathbf {e} }}^{i}}$ , podemos concluir que ${textstyle F^{i}={hat {F}}^{i}/{sqrt {g_{ii}}}}$ . Después de sustituir, la fórmula se convierte en:

{displaystyle operatorname {div} (mathbf {F})={frac {1}{rho }}{frac {partial left({frac {rho }{sqrt {g_{ii}}}}{hat {F}}^{i}right)}{partial x^{i}}}={frac {1}{sqrt {det g}}}{frac {partial left({sqrt {frac {det g}{g_{ii}}}},{hat {F}}^{i}right)}{partial x^{i}}}.}

Ver § En coordenadas curvilíneas para más información.

Propiedades

Las siguientes propiedades se pueden derivar de las reglas ordinarias de diferenciación del cálculo. Lo más importante es que la divergencia es un operador lineal, es decir,

{displaystyle operatorname {div} (amathbf {F} +bmathbf {G})=aoperatorname {div} mathbf {F} +boperatorname {div} mathbf {G} }

para todos los campos vectoriales $F$ y $G$ y todos números reales $a$ y $b$ .

Existe una regla de producto del siguiente tipo: si $φ$ es una función con valores escalares y $F$ es un campo vectorial, entonces

{displaystyle operatorname {div} (varphi mathbf {F})=operatorname {grad} varphi cdot mathbf {F} +varphi operatorname {div} mathbf {F}}

o en una notación más sugerente

{displaystyle nabla cdot (varphi mathbf {F})=(nabla varphi)cdot mathbf {F} +varphi (nabla cdot mathbf {F}).}

Otra regla del producto para el producto vectorial de dos campos vectoriales $F$ y $G$ en tres dimensiones implica el rizo y dice lo siguiente:

{displaystyle operatorname {div} (mathbf {F} times mathbf {G})=operatorname {curl} mathbf {F} cdot mathbf {G} -mathbf {F} cdot operatorname {curl} mathbf {G}}

{displaystyle nabla cdot (mathbf {F} times mathbf {G})=(nabla times mathbf {F})cdot mathbf {G} -mathbf {F} cdot (nabla times mathbf {G}).}

El Laplaciano de un campo escalar es la divergencia del gradiente del campo:

{displaystyle operatorname {div} (operatorname {grad} varphi)=Delta varphi.}

La divergencia del rotacional de cualquier campo vectorial (en tres dimensiones) es igual a cero:

{displaystyle nabla cdot (nabla times mathbf {F})=0.}

Si se define un campo vectorial $F$ con divergencia cero en una bola en $R 3$ , entonces existe algún campo vectorial $G$ en la pelota con $F = curl G$ . Para regiones en $R 3$ topológicamente más complicadas que esta, la última declaración podría ser falsa (ver el lema de Poincaré). El grado de fallo de la verdad del enunciado, medido por la homología del complejo de cadenas

{displaystyle {{text{scalar fields on }}U}~{overset {operatorname {grad} }{rightarrow }}~{{text{vector fields on }}U}~{overset {operatorname {curl} }{rightarrow }}~{{text{vector fields on }}U}~{overset {operatorname {div} }{rightarrow }}~{{text{scalar fields on }}U}}

sirve como una buena cuantificación de la complejidad de la región subyacente $U$ . Estos son los inicios y principales motivaciones de la cohomología de De Rham.

Teorema de descomposición

Se puede demostrar que cualquier flujo estacionario $v (r)$ que es dos veces continuamente diferenciable en $R 3$ y desaparece lo suficientemente rápido para $| r | \to \infty$ se puede descomponer únicamente en una parte irrotacional $E (r)$ y una parte sin fuente $B (r)$ . Además, estas partes están explícitamente determinadas por las respectivas densidades de fuente (ver arriba) y densidades de circulación (ver el artículo Curl):

Para la parte irrotacional se tiene

{displaystyle mathbf {E} =-nabla Phi (mathbf {r}),}

con

{displaystyle Phi (mathbf {r})=int _{mathbb {R} ^{3}},d^{3}mathbf {r} ';{frac {operatorname {div} mathbf {v} (mathbf {r} ')}{4pi left|mathbf {r} -mathbf {r} 'right|}}.}

La parte libre de fuente, $B$ , se puede escribir de manera similar: uno solo tiene que reemplazar el potencial escalar $Φ(r)$ por un vector potencial $A (r)$ y los términos $-\nablaΦ$ por $+\nabla \times A$ y la densidad de origen $div v$ por la densidad de circulación $\nabla \times v$ .

Este "teorema de descomposición" es un subproducto del caso estacionario de la electrodinámica. Es un caso especial de la descomposición de Helmholtz más general, que también funciona en dimensiones mayores de tres.

En dimensiones finitas arbitrarias

La divergencia de un campo vectorial se puede definir en cualquier número finito $n$ de dimensiones. Si

{displaystyle mathbf {F} =(F_{1},F_{2},ldots F_{n}),}

en un sistema de coordenadas euclidianas con coordenadas $x 1, x 2,..., x n$ , definir

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} ={frac {partial F_{1}}{partial x_{1}}}+{frac {partial F_{2}}{partial x_{2}}}+cdots +{frac {partial F_{n}}{partial x_{n}}}.}

En el caso 1D, $F$ se reduce a una función regular y la divergencia se reduce a la derivada.

Para cualquier $n$ , la divergencia es un operador lineal y cumple la "regla del producto"

{displaystyle nabla cdot (varphi mathbf {F})=(nabla varphi)cdot mathbf {F} +varphi (nabla cdot mathbf {F})}

para cualquier función con valores escalares $φ$ .

Relación con la derivada exterior

Se puede expresar la divergencia como un caso particular de la derivada exterior, que toma una forma 2 a una forma 3 en $R 3$ . Defina la forma actual de dos formas como

{displaystyle j=F_{1},dywedge dz+F_{2},dzwedge dx+F_{3},dxwedge dy.}

Mide la cantidad de "cosas" que fluye a través de una superficie por unidad de tiempo en un "fluido de relleno" de densidad $ρ = 1 dx \land dy \land dz$ moviéndose con velocidad local $F$ . Su derivada exterior $dj$ viene dada por

{displaystyle dj=left({frac {partial F_{1}}{partial x}}+{frac {partial F_{2}}{partial y}}+{frac {partial F_{3}}{partial z}}right)dxwedge dywedge dz=(nabla cdot {mathbf {F} })rho }

Donde $wedge$ es el producto de cuña.

Por lo tanto, la divergencia del campo vectorial $F$ se puede expresar como:

{displaystyle nabla cdot {mathbf {F} }={star }d{star }{big (}{mathbf {F} }^{flat }{big)}.}

Aquí el superscript . es uno de los dos isomorfismos musicales, y $⋆$ es el operador estrella Hodge. Cuando la divergencia está escrita de esta manera, el operador ${displaystyle {star }d{star }}$ se denomina codiferencial. Trabajar con las dos formas actuales y el derivado exterior es generalmente más fácil que trabajar con el campo vectorial y la divergencia, porque a diferencia de la divergencia, el derivado exterior se comunica con un cambio de sistema de coordenadas (curvilinear).

En coordenadas curvilíneas

La expresión apropiada es más complicada en coordenadas curvilíneas. La divergencia de un campo vectorial se extiende naturalmente a cualquier variedad diferenciable de dimensión $n$ que tiene una forma de volumen (o densidad) $μ$ , p. ej. una variedad riemanniana o lorentziana. Generalizando la construcción de dos formas para un campo vectorial en $R 3$ , en tal variedad de campos vectoriales $X$ define una $(n - 1)$ -forma j = i_X μ obtenido contrayendo $X$ con $μ$ . La divergencia es entonces la función definida por

{displaystyle dj=(operatorname {div} X)mu.}

La divergencia se puede definir en términos de la derivada de Lie como

{displaystyle {mathcal {L}}_{X}mu =(operatorname {div} X)mu.}

Esto significa que la divergencia mide la tasa de expansión de una unidad de volumen (un elemento de volumen) a medida que fluye con el campo vectorial.

En una variedad pseudo-Riemanniana, la divergencia con respecto al volumen se puede expresar en términos de la conexión Levi-Civita $\nabla$ :

{displaystyle operatorname {div} X=nabla cdot X={X^{a}}_{;a},}

donde la segunda expresión es la contracción del campo vectorial valorado en 1 forma $\nabla X$ consigo mismo y la última expresión es la expresión de coordenadas tradicional del cálculo de Ricci.

Una expresión equivalente sin usar una conexión es

{displaystyle operatorname {div} (X)={frac {1}{sqrt {left|det gright|}}},partial _{a}left({sqrt {left|det gright|}},X^{a}right),}

Donde $g$ es la métrica y $partial _{a}$ denota el derivado parcial con respecto a la coordinación $x a$ . La raíz cuadrada de la métrica (valor absoluto del determinante) aparece porque la divergencia debe ser escrita con la correcta concepción del volumen. En coordenadas curvilinear, los vectores base ya no son ortonormales; el determinante codifica la idea correcta del volumen en este caso. Parece dos veces, aquí, una vez, así que ${displaystyle X^{a}}$ se puede transformar en "espacio plano" (donde las coordenadas son ortonormales), y una vez más para que $partial _{a}$ también se transforma en "espacio plano", para que finalmente, la divergencia "ordinaria" pueda ser escrita con el concepto "ordinario" del volumen en espacio plano (i.e. volumen de unidad i.e. uno, i.e. no escrito). La raíz cuadrada aparece en el denominador, porque el derivado se transforma de la manera opuesta (contravariante) al vector (que es covariante). Esta idea de llegar a un "sistema de coordenadas planas" donde se pueden hacer computaciones locales de forma convencional se llama un vielbein. Una manera diferente de ver esto es notar que la divergencia es la codiferencial disfrazada. Es decir, la divergencia corresponde a la expresión ${displaystyle star dstar }$ con $d$ el diferencial y $star$ la estrella Hodge. La estrella Hodge, por su construcción, hace que la forma de volumen aparezca en todos los lugares adecuados.

La divergencia de los tensores

La divergencia también se puede generalizar a los tensores. En la notación de Einstein, la divergencia de un vector contravariante $F μ$ viene dado por

{displaystyle nabla cdot mathbf {F} =nabla _{mu }F^{mu },}

donde $\nabla μ$ denota la derivada covariante. En este marco general, la formulación correcta de la divergencia es reconocer que es un codiferencial; las propiedades apropiadas se siguen de allí.

De manera equivalente, algunos autores definen la divergencia de un tensor mixto usando el isomorfismo musical ♯: si $T$ es un $(p, q)$ -tensor ( $p$ para el vector contravariante y $q$ para la covariante), luego definimos la divergencia de $T$ para ser el $(p, q - 1)$ -tensor

{displaystyle (operatorname {div} T)(Y_{1},ldotsY_{q-1})={operatorname {trace} }{Big (}Xmapsto sharp (nabla T)(X,cdotY_{1},ldotsY_{q-1}){Big)};}

es decir, tomamos el rastro sobre el primero dos índices covariantes del derivado covariante. El $sharp$ símbolo se refiere al isomorfismo musical.

Contenido relacionado

Más resultados...