Distribución t de Student
En probabilidad y estadística, la distribución t del estudiante (o simplemente la distribución t) es cualquier miembro de una familia de distribuciones de probabilidad continuas que surgen al estimar la media de una población distribuida normalmente en situaciones en las que el tamaño de la muestra es pequeño y se desconoce la desviación estándar de la población. Fue desarrollado por el estadístico inglés William Sealy Gosset bajo el seudónimo de "Student".
La distribución t juega un papel en una serie de análisis estadísticos ampliamente utilizados, incluida la prueba t de Student para evaluar la significación estadística de la diferencia entre dos medias de muestra, la construcción de intervalos de confianza para la diferencia entre dos medias poblacionales, y en análisis de regresión lineal. La distribución t de Student también surge en el análisis bayesiano de datos de una familia normal.
Si tomamos una muestra n{displaystyle n} observaciones de una distribución normal, luego t-distribución con .. =n− − 1{displaystyle nu =n-1} grados de libertad se puede definir como la distribución de la ubicación de la muestra significa relativa a la verdadera media, dividida por la desviación estándar de la muestra, después de multiplicarse por el término estandarizado n{displaystyle {sqrt {n}}. De esta manera, la t- La distribución se puede utilizar para construir un intervalo de confianza para la verdadera media.
La distribución t es simétrica y tiene forma de campana, como la distribución normal. Sin embargo, la distribución t tiene colas más pesadas, lo que significa que es más propensa a producir valores que caen lejos de su media. Esto lo hace útil para comprender el comportamiento estadístico de ciertos tipos de razones de cantidades aleatorias, en las que la variación en el denominador se amplifica y puede producir valores atípicos cuando el denominador de la razón cae cerca de cero. La distribución t de Student es un caso especial de la distribución hiperbólica generalizada.
Historia y etimología
En estadística, la distribución t se derivó por primera vez como una distribución posterior en 1876 por Helmert y Lüroth. La distribución t también apareció en una forma más general como distribución de Pearson Tipo IV en el artículo de Karl Pearson de 1895.
En la literatura en inglés, la distribución toma su nombre del artículo de 1908 de William Sealy Gosset en Biometrika bajo el seudónimo de "Student". Una versión del origen del seudónimo es que el empleador de Gosset prefería que el personal usara seudónimos al publicar artículos científicos en lugar de su nombre real, por lo que usó el nombre "Estudiante" para ocultar su identidad. Otra versión es que Guinness no quería que sus competidores supieran que estaban usando la prueba t para determinar la calidad de la materia prima.
Gosset trabajó en Guinness Brewery en Dublín, Irlanda, y estaba interesado en los problemas de las muestras pequeñas; por ejemplo, las propiedades químicas de la cebada, donde los tamaños de muestra pueden ser de tan solo 3. El artículo de Gosset se refiere a la distribución como la "distribución de frecuencia de las desviaciones estándar de muestras extraídas de una población normal". Se hizo muy conocido a través del trabajo de Ronald Fisher, quien llamó a la distribución "distribución del estudiante" y representó el valor de la prueba con la letra t.
Cómo surge la distribución de Student a partir del muestreo
Vamos X1,...... ,Xn{textstyle X_{1},ldots X_{n} de la distribución N()μ μ ,σ σ 2){displaystyle {mathcal {N}(musigma ^{2}}Es una muestra de tamaño n{displaystyle n} de una población normalmente distribuida con valor medio esperado μ μ {displaystyle mu } y diferencia σ σ 2{displaystyle sigma ^{2}.
Dejar
- X̄ ̄ =1n.. i=1nXi{displaystyle {bar {X}={frac {1}{n}sum} ¿Qué?
sea la media muestral y sea
- S2=1n− − 1.. i=1n()Xi− − X̄ ̄ )2{displaystyle S^{2}={frac {1}{n-1}sum ¿Qué?
sea la varianza muestral (corregida por Bessel). Entonces la variable aleatoria
- X̄ ̄ − − μ μ σ σ /n{displaystyle {frac {f}-mu}{sigma /{sqrt {n}}}}} {f}}}}
tiene una distribución normal estándar (es decir, normal con media esperada 0 y varianza 1), y la variable aleatoria
- X̄ ̄ − − μ μ S/n{displaystyle {frac {f}-mu} }{S/{sqrt {}}}
i.e Donde S{displaystyle S. ha sido sustituida σ σ {displaystyle sigma }, tiene un estudiante t-distribución con n− − 1{displaystyle n-1} grados de libertad. Desde S{textstyle S} sustituido σ σ ,{textstyle sigma} la única cantidad inservible en esta expresión es μ μ ,{textstyle mu} para que esto pueda utilizarse para obtener intervalos de confianza μ μ .{textstyle mu.} El numerador y el denominador en la expresión anterior son variables aleatorias estadísticamente independientes a pesar de estar basadas en la misma muestra X1,...... ,Xn{textstyle X_{1},ldots X_{n}. Esto se puede ver observando que cov ()X̄ ̄ ,Xi− − X̄ ̄ )=0,{textstyle operatorname {cov} ({overline {X}},,X_{i}-{overline {X}})=0,} y recordando que X̄ ̄ {textstyle {fnline {X}} y Xi− − X̄ ̄ {textstyle X_{i}-{overline {X}} son ambas combinaciones lineales del mismo conjunto de i.i.d. normalmente distribuidas variables aleatorias.
Definición
Función de densidad de probabilidad
La t-distribución del estudiante tiene la función de densidad de probabilidad (PDF) dada por
- f()t)=.. ().. +12).. π π .. ().. 2)()1+t2.. )− − ().. +1)/2,{displaystyle f(t)={frac {fnMicrosoft Sans Serif} {sqrt {nu pi}}} {sqrt {nu pi} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicroc {f}}}}}right)}{-(nu +1)/2}
Donde .. {displaystyle nu } es el número de grados de libertad y .. {displaystyle "Gamma" es la función gamma. Esto también puede ser escrito como
- f()t)=1.. B()12,.. 2)()1+t2.. )− − ().. +1)/2,{displaystyle f(t)={frac {1}{sqrt {fn} {fnMicroc {2}}}}}left(1+{frac {2} {nu }}}}}}}}}}left(1+{frac {t^{2}{nu }right)}{-(nu +1)/2}}}}}}}}}}}}}}
donde B es la función Beta. En particular, para los grados más valorados de la libertad .. {displaystyle nu } tenemos:
Para 1}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■1{displaystyle nu1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/67dc59709ea03ee8535240205566d3e844bd2b66" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/> incluso,
- .. ().. +12).. π π .. ().. 2)=().. − − 1)().. − − 3)⋯ ⋯ 5⋅ ⋅ 32.. ().. − − 2)().. − − 4)⋯ ⋯ 4⋅ ⋅ 2⋅ ⋅ {displaystyle {frac {Gamma ({frac {nu +1}{2}}}{sqrt {nu pi {fnK}}}={frac {nu -1)cdots 5cdots 3}{2{sqrt {nu }}(nu -2)(nu -4)cdots 4cdot 2,}cdot }cdot }cdot }cdot }cdot }
Para 1}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■1{displaystyle nu1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/67dc59709ea03ee8535240205566d3e844bd2b66" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/> extraño.
- .. ().. +12).. π π .. ().. 2)=().. − − 1)().. − − 3)⋯ ⋯ 4⋅ ⋅ 2π π .. ().. − − 2)().. − − 4)⋯ ⋯ 5⋅ ⋅ 3⋅ ⋅ {displaystyle {frac {Gamma ({frac {nu +1}{2}}}{sqrt {nu pi {fnMicrosoft Sans Serif} {nMicrosoft Sans Serif} {nMicroc {nu -1)(nu -3)cdots 4cdot 2}{pi {sqrt {nu } {nu }(nu -2)(nu -4)cdots 5cdot 3,}cdot }cdot }cdot }cdot }cdot }cdot }cdot }cdot }cdot !
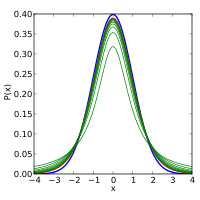
La función de densidad de probabilidad es simétrica, y su forma global se asemeja a la forma de campana de una variable normalmente distribuida con media 0 y varianza 1, excepto que es un poco más baja y más amplia. A medida que crece el número de grados de libertad, t- La distribución se aproxima a la distribución normal con media 0 y varianza 1. Por esta razón .. {displaystyle {nu}} también se conoce como el parámetro normalidad.
Las siguientes imágenes muestran la densidad de la t-distribución para aumentar los valores .. {displaystyle nu }. La distribución normal se muestra como una línea azul para la comparación. Note que t- La distribución (línea roja) se acerca más a la distribución normal como .. {displaystyle nu } aumenta.
Función de distribución acumulativa
La función de distribución acumulativa (CDF) se puede escribir en términos de I, la regularizada función beta incompleta. Para t > 0,
- F()t)=∫ ∫ − − JUEGO JUEGO tf()u)du=1− − 12Ix()t)().. 2,12),{displaystyle F(t)=int _{-infty }{t}f(u),du=1-{tfrac {1}{2}}I_{x(t)}left({tfrac {nu }{2}}} {tfrac {1} {2}}}derecho),}}}
dónde
- x()t)=.. t2+.. .{displaystyle x(t)={frac {nu }{t^{2}+nu }}
Otros valores serían obtenidos por simetría. Una fórmula alternativa, válida para <math alttext="{displaystyle t^{2}t2... {displaystyle t^{2}traducidonu}<img alt="t^2 , es
- ∫ ∫ − − JUEGO JUEGO tf()u)du=12+t.. ()12().. +1))π π .. .. ().. 2)2F1()12,12().. +1);32;− − t2.. ),{displaystyle int _{-infty }{t}f(u),du={tfrac {1}{2}+t{frac} {nMicrosoft Sans Serif} {nMicrosoft Sans Serif} {fnMicrosoft Sans Serif}},\nMicros {nMicroc {nMicroc}}}}}, {fnMicroc} {fnMicroc}}} {fnMicroc}}}}ccH0} {f}c}c}c}cH0}c}cH0}ccccH0}ccH0}cccH0ccH00}cH00}cH00}cH00}ccccH00}cH00}ccH0}ccH00}ccH00}cH00}cH00}cH00}cH00}cH00}ccH0}cH00}cH00}cH00} {1}{2}},{tfrac {1}{2} {nu +1);{tfrac {3}{2};-{tfrac {t^{2}{nu}right),}
donde 2F1 es un caso particular de la función hipergeométrica.
Para obtener información sobre su función de distribución acumulativa inversa, consulte la función cuantil § Distribución t de Student.
Casos especiales
Ciertos valores .. {displaystyle nu } da una forma sencilla para la t-distribución de Student.
| .. {displaystyle nu } | CDF | Notas | |
|---|---|---|---|
| 1 | 1π π ()1+t2){displaystyle {frac {1}{=+t^{2}}} | 12+1π π arctan ()t){displaystyle {frac {2}}+{frac {1}{pi}arctan(t)} | Ver distribución de Cauchy |
| 2 | 122()1+t22)3/2{displaystyle {frac {1}{2{sqrt {2}left(1+{frac {t^{2}}{2}}}right)}}}}}}}} {c}}}}}} {c}}}}}}}} {c}}}}}}}}}}}}}}}}}}}} { | 12+t221+t22{fnMicroc} {1}{2}+{frac {t}{2{sqrt {2}{sqrt {1+{frac} {}}}} | |
| 3 | 2π π 3()1+t23)2{displaystyle {frac {2}{f} {fnMicrosoft}} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {fnK}}}} {fnK}}}}}} {f}}f}}}f}fnKfnK}}}}}}}}} {sqrt {3}left(1+{frac {t}{3}right)}}}}}}}} | 12+1π π [13t1+t23+arctan ()t3)]{fnMicroc} {fn} {fn} {fn} {fn}} {fn}}} {fn}} {fn}}} {fn}}} {fn}}} {fn}}}} {fn}}}}} {f}}} {f}}}} {f}}}}} {f}}}} {f}}}}}}} {f}}}}}}}}}}}}} {f}}}} {f}}}} {f}}}} {f}}}}}} {f}}}}}}}}}} {f}}}}} {f}} {f} {f}}}}}}} {f}}} {f}}}}}}f}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {T}{1+{frac} {fnMicroc {}}derecha]}}} | |
| 4 | 38()1+t24)5/2{displaystyle {frac {3}{5/2}}}} | 12+38t1+t24[1− − 112t21+t24]{displaystyle {frac}{2}+{frac {3}{}{frac}}{frac} {f}} {f}}} {f}}}} {f} {f}}} {f}} {f}}} {f}f}}}}}}}}}}}} {f} {T}{sqrt {1+{frac {fnK}}} {fnMift[1-{frac}}} {f}}}}} {f}}}} {f}}}}} {f}}}}}}}} {m}}} {f}}}}}}}} {f}}}}}}}}}}}} { {1}{12} {frac {2}{1+{frac} {f} {f}} {f} {f}} {f}}}}} {1+ {f} {f}} {f}}} {f}} {f}} {f}} {f}} {f}}} {f}}} {f} {f} {f}}}}}f} {f}f}f}f} {f}} {f}f} {f} {f} {f} {f} {f}f}f}f} {f}f}f} {f}f} {f}f} {f}f} {f}f}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} | |
| 5 | 83π π 5()1+t25)3{displaystyle {frac}{3pi} {sqrt {5}left(1+{frac {t^{2}{5}right)}}}}}} | 12+1π π [t5()1+t25)()1+23()1+t25))+arctan ()t5)]{fnK} {fnK}} {fnh} {fnh} {fnh} {fn} {fn}} {fn}}} {fnfnfn}} {fnfn}} {fnfnf}}}}}}}}}}}}}} {f}}f}}} {f}}}} {f}}}}}fnfnfnfnfnf}f}fnf}fnfnfnfnfnfnf}}}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}}}}}}}}fnfnfnfn}}}}}}}}}}}}}} {} {fn}}} {fnMicroc {fn} {fnfn}}}}}}left(1+{frac {2}{3left(1+frac {}{2}{5}}}right)}}}}right)+arctanleft({frac} {f} {f} {} {f}} {}}}}}}} {}}}}}}} {}}}}}}}}} {} {}}} {}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} | |
| JUEGO JUEGO {displaystyle infty } | 12π π e− − t2/2{displaystyle {frac {1}{sqrt {2pi}}e^{-t^{2}/2}} | 12[1+er ()t2)]{displaystyle {frac {2}{left[1+operatorname {erf} left({frac {t}{sqrt {2}}}right)}}}}}} {derecha]}}}} {derecha]}}} {derecha}}}}}}}}}}}}}}} | Ver Distribución normal, función de error |
Cómo surge la distribución t
Distribución de muestras
Vamos x1,...... ,xn{displaystyle x_{1},ldotsx_{n} los números observados en una muestra de una población distribuida continuamente con valor esperado μ μ {displaystyle mu }. La media muestra y la varianza de muestra se dan por:
- x̄ ̄ =x1+⋯ ⋯ +xnn,s2=1n− − 1.. i=1n()xi− − x̄ ̄ )2.{displaystyle {begin{aligned}{bar {x} {fnMicroc} {x_{1}+cdots ################################################################################################################################################################################################################################################################ ¿Qué? {x})} {2}end{aligned}}
El valor t resultante es
- t=x̄ ̄ − − μ μ s/n.{displaystyle t={frac {{bar {x}-mu }{s/{sqrt.
El t-distribución con n− − 1{displaystyle n-1} grados de libertad es la distribución del muestreo t-valor cuando las muestras consisten en observaciones independientes distribuidas idénticamente de una población normalmente distribuida. Así, con fines de inferencia t es una cantidad útil "pivotal" en el caso cuando la media y la varianza ()μ μ ,σ σ 2){displaystyle (musigma ^{2})} son parámetros de población desconocidos, en el sentido de que t- el valor tiene entonces una distribución de probabilidad que no depende de μ μ {displaystyle mu } ni σ σ 2{displaystyle sigma ^{2}.
Inferencia bayesiana
En las estadísticas bayesianas, una distribución t (escalada, desplazada) surge como la distribución marginal de la media desconocida de una distribución normal, cuando la dependencia de una varianza desconocida ha sido marginada:
- p()μ μ ▪ ▪ D,I)=∫ ∫ p()μ μ ,σ σ 2▪ ▪ D,I)dσ σ 2=∫ ∫ p()μ μ ▪ ▪ D,σ σ 2,I)p()σ σ 2▪ ▪ D,I)dσ σ 2,{displaystyle {begin{aligned}p(mumid D,I)= limitint p(musigma ^{2}mid D,I),dsigma ^{2}= limitint p(mumid D,sigma ^{2},I)psigma
Donde D{displaystyle D} significa que los datos {}xi}{displaystyle {x_{i}}}, y I{displaystyle Yo... representa cualquier otra información que pueda haber sido utilizada para crear el modelo. La distribución es por lo tanto el agravamiento de la distribución condicional μ μ {displaystyle mu } dados los datos y σ σ 2{displaystyle sigma ^{2} con la distribución marginal σ σ 2{displaystyle sigma ^{2} dados los datos.
Con n{displaystyle n} puntos de datos, si no informativos, o planos, la ubicación previa p()μ μ ▪ ▪ σ σ 2,I)=const{displaystyle p(mu mid sigma ^{2},I)={text{const}} se puede tomar para μ, y la escala anterior p()σ σ 2▪ ▪ I)∝ ∝ 1/σ σ 2{displaystyle p(sigma ^{2}mid I)propto 1/sigma ^{2} se puede tomar para σ2Entonces el teorema de Bayes da
- p()μ μ ▪ ▪ D,σ σ 2,I)♪ ♪ N()x̄ ̄ ,σ σ 2/n),p()σ σ 2▪ ▪ D,I)♪ ♪ Scale-inv- χ χ 2().. ,s2),{displaystyle {begin{aligned}p(mu mid D,sigma ^{2},I) limitsim N({bar {x}},sigma ^{2}/n),p(sigma ^{2}mid D,I) Duesim operatorname {Scale-inv-}2}chi
una distribución normal y una distribución inversa escuadrada inversa, respectivamente, donde .. =n− − 1{displaystyle nu =n-1} y
- s2=.. ()xi− − x̄ ̄ )2n− − 1.{displaystyle {fn1}}
La integral de marginación se convierte así en
- p()μ μ ▪ ▪ D,I)∝ ∝ ∫ ∫ 0JUEGO JUEGO 1σ σ 2exp ()− − 12σ σ 2n()μ μ − − x̄ ̄ )2)⋅ ⋅ σ σ − − .. − − 2exp ()− − .. s2/2σ σ 2)dσ σ 2∝ ∝ ∫ ∫ 0JUEGO JUEGO σ σ − − .. − − 3exp ()− − 12σ σ 2()n()μ μ − − x̄ ̄ )2+.. s2))dσ σ 2.{fnMicrosoft Sans Serif} {0} {fnK} {fnMicrosoft Sans Serif} {fnfnK} {fnMicroc {1}{2sigma ^{2}}left(n(mu -bar {x})}{2}+nu s^{2}right)derecha)dsigma }{2}}}}}}}}}}}}}}}nun}}nun}nun}}nun}nun}}}}}}}}}nun}nun}nunnun}nunnun}nun}nun}nun}nunnun}nun}nunnun}nun}nun}nunnunnunnunnun}nun}nun}nunnun}nunnunnun}nun}nun}nun}
Esto se puede evaluar mediante sustitución z=A/2σ σ 2{displaystyle z=A/2sigma }, donde A=n()μ μ − − x̄ ̄ )2+.. s2{displaystyle A=n(mu -{bar {x}}{2}+nu s^{2}, dar
- dz=− − A2σ σ 4dσ σ 2,{displaystyle dz=-{2sigma },dsigma ^{2}
entonces
- p()μ μ ▪ ▪ D,I)∝ ∝ A− − ().. +1)/2∫ ∫ 0JUEGO JUEGO z().. − − 1)/2exp ()− − z)dz.{displaystyle p(mumid D,I)propto A^{-(nu +1)/2}int _{0}^{infty }z^{(nu -1)/2}exp(-z),dz.}
Pero la integral z ahora es una integral gamma estándar, que se evalúa como una constante, dejando
- p()μ μ ▪ ▪ D,I)∝ ∝ A− − ().. +1)/2∝ ∝ ()1+n()μ μ − − x̄ ̄ )2.. s2)− − ().. +1)/2.{displaystyle {begin{aligned}p(mumid D,I) limitepropto A^{-(nu +1)/2}\\ Ummcfn(mu -bar {x})}{2}}}{2}}}}}right){-(nu +1)/2}} {endnu}{}}}} {}}}}{}}}}}}{}}}}}}}}{}}{}}}}{}}}} {}}{}}}}}} {}}}}}}{}}}}{}}}}}}}}} {}}}}}}}}}}}} {}}}} {}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}{}}}}}}}}}}}}} {
Esta es una forma de distribución t con una escala y un cambio explícitos que se explorarán con más detalle en una sección adicional a continuación. Se puede relacionar con la distribución t estandarizada por la sustitución
- t=μ μ − − x̄ ̄ s/n.{displaystyle t={frac {fnMicroc} - {bar {x} {fn}{sqrt.
La derivación anterior se ha presentado para el caso de antecedentes no informativos para μ μ {displaystyle mu } y σ σ 2{displaystyle sigma ^{2}; pero será evidente que cualquier previo que lleve a una distribución normal que se componga con una distribución inversa inversa de chi-squared conducirá a una t-distribución con escala y cambio para P()μ μ ▪ ▪ D,I){displaystyle P(mumid D,I)}, aunque el parámetro de escalado correspondiente a s2n{displaystyle {frac {fn} {fn}} {fn}} {fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}} {fn}}}} {fn}}}}} {fn}}}}}}}}} arriba será influenciado tanto por la información anterior como por los datos, en lugar de simplemente por los datos como arriba.
Caracterización
Como la distribución de una estadística de prueba
Estudiante t-distribución con .. {displaystyle nu } grados de libertad se puede definir como la distribución de la variable aleatoria T con
- T=ZV/.. =Z.. V,{displaystyle T={frac {Z}{sqrt {V/nu} - Sí. ♪♪
dónde
- Z es una norma normal con el valor esperado 0 y la diferencia 1;
- V tiene una distribución de chi-squared (χ2-distribuciónCon .. {displaystyle nu } grados de libertad;
- Z y V son independientes;
Se define una distribución diferente como la de la variable aleatoria definida, para una constante dada μ, por
- ()Z+μ μ ).. V.{displaystyle (Z+mu){sqrt {frac {nu - Sí.
Esta variable aleatoria tiene una distribución t no central con parámetro de no centralidad μ. Esta distribución es importante en los estudios de la potencia de la prueba t de Student.
Derivación
Suponga que X1,..., Xn son independientes realizaciones de la variable aleatoria normalmente distribuida X, que tiene un valor esperado μ y una varianza σ2. Dejar
- X̄ ̄ n=1n()X1+⋯ ⋯ +Xn){displaystyle {fn} {fn}={fn}= {fnK}} {fn}}} {\fn}}= {fn}fn}fn}fn}\fn\fn\fnhfn}\fnKfnK\fn}\fnhnhnhnhnhn}}}\\\\fnK\\fnKfnKfnKfn}\fnh00}\\\\\fnKfnK\fnh\\fnhnKfnhnKfnhnhnhnhnhnhnhnhnKfnhnhnh00}fnhnhnhnhnhnhnh}\\\\\\\\\\ {1}{n}(X_{1}+cdots +X_{n}}
sea la media muestral, y
- Sn2=1n− − 1.. i=1n()Xi− − X̄ ̄ n)2{displaystyle S_{n}{2}={frac {1}{n-1}sum ¿Por qué? {X}_{n}right)}{2}
ser una estimación imparcial de la varianza de la muestra. Se puede demostrar que la variable aleatoria
- V=()n− − 1)Sn2σ σ 2{displaystyle V=(n-1){frac {fn} {fn} {fn}} {fn}}}} {fn}}}}} {fn}}}} {fn}}}}}}}}}}}}}}}}} {cH}}}}}}}}}} {sigma
tiene una distribución de chi-squared con .. =n− − 1{displaystyle nu =n-1} grados de libertad (por el teorema de Cochran). Se muestra fácilmente que la cantidad
- Z=()X̄ ̄ n− − μ μ )nσ σ {displaystyle Z=left({overline {X}_{n}-muright){frac {sqrt {n}{sigma }
se distribuye normalmente con media 0 y varianza 1, ya que el promedio de la muestra X̄ ̄ n{displaystyle {fnK} {fn} {fn}} {fn}}} {fn}}}} {fn}}} {fn}}}}}} {fn}}}}}}} {fn}}}}}}}} {fn}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { se distribuye normalmente con media μ y diferencia σ2/n. Además, es posible demostrar que estas dos variables aleatorias (las normalmente distribuidas Z y el chi-squared-distribuido uno V) son independientes. En consecuencia, la cantidad pivotal
- T↑ ↑ ZV/.. =()X̄ ̄ n− − μ μ )nSn,{textstyle Tequiv {frac {Z}{sqrt {V/nu}=left({overline {X}_{n}-muright){frac {sqrt {n} {S_{n}}}}
que difiere de Z en que la desviación estándar exacta σ es reemplazado por la variable aleatoria Sn, tiene un estudiante t-distribución como se define anteriormente. Observe que la diferencia de población desconocida σ2 no aparece T, ya que estaba en el numerador y el denominador, así que canceló. Gosset obtuvo intuitivamente la función de densidad de probabilidad indicada anteriormente, con .. {displaystyle nu } iguales n1, y Fisher lo demostró en 1925.
La distribución de la estadística de prueba T depende de .. {displaystyle nu }, pero no μ o σ; la falta de dependencia μ y σ es lo que hace t-distribución importante tanto en teoría como en práctica.
Como distribución máxima de entropía
Estudiante t-distribución es la distribución máxima de probabilidad de entropía para un variato aleatorio X para la cual E ()In ().. +X2)){displaystyle operatorname {E} (ln(nu +X^{2})} está arreglado.
Propiedades
Momentos
Para 1}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■1{displaystyle nu 1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/67dc59709ea03ee8535240205566d3e844bd2b66" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/>, los momentos crudos de t- La distribución es
- <math alttext="{displaystyle operatorname {E} (T^{k})={begin{cases}0&k{text{ odd}},quad 0<k<nu \{frac {1}{{sqrt {pi }}Gamma left({frac {nu }{2}}right)}}left[Gamma left({frac {k+1}{2}}right)Gamma left({frac {nu -k}{2}}right)nu ^{frac {k}{2}}right]&k{text{ even}},quad 0<kE ()Tk)={}0kextraño,0.k... 1π π .. ().. 2)[.. ()k+12).. ().. − − k2).. k2]kincluso,0.k... .{displaystyle operatorname {E} (T^{k}={begin{cases}0 recurk{text{ odd},quad 0 se realizó \nu{frac {1}{sqrt {cH00} {cH00} {cH00} {cH00} {cH00}} {cH00} {cH00}} {cHFF} {cHFF} {cHFF} {cH00}} {ccH00}} {cH00}} {cHFF} {cHFF}}}} {cHFF}} {cccH}}}} {cccH00} {cHFF} {cccccccccccccccccHFF} {cHFF}} {cccccccccccccccccHFF}} {cccccccccHFF} {ccc }Gammaleft({frac {nu }{2}right)}left[Gamma left({frac {k+1}{2}right)Gammaleft({frac {nu - Está bien. {k}{2}right] diezk{text{ even},quad 0 obtenidosk madenu.\\end{cases}}<img alt="{displaystyle operatorname {E} (T^{k})={begin{cases}0&k{text{ odd}},quad 0<k<nu \{frac {1}{{sqrt {pi }}Gamma left({frac {nu }{2}}right)}}left[Gamma left({frac {k+1}{2}}right)Gamma left({frac {nu -k}{2}}right)nu ^{frac {k}{2}}right]&k{text{ even}},quad 0<k
Momentos de orden .. {displaystyle nu } o superior no existen.
El término para <math alttext="{displaystyle 0<k0.k... {displaystyle 0 se hizo realidad<img alt="0 < k , k incluso, puede ser simplificado utilizando las propiedades de la función gamma para
- <math alttext="{displaystyle operatorname {E} (T^{k})=nu ^{frac {k}{2}},prod _{i=1}^{k/2}{frac {2i-1}{nu -2i}}qquad k{text{ even}},quad 0<kE ()Tk)=.. k2∏ ∏ i=1k/22i− − 1.. − − 2ikincluso,0.k... .{displaystyle operatorname {fnMicrosoft Sans Serif} {k}{2},prod ##{i=1} {k/2}{frac {2i-1}{nu -2i}qquad k{text{ even},quad 0 se hizo realidadnu.}<img alt="{displaystyle operatorname {E} (T^{k})=nu ^{frac {k}{2}},prod _{i=1}^{k/2}{frac {2i-1}{nu -2i}}qquad k{text{ even}},quad 0<k
Para un t-distribución con .. {displaystyle nu } grados de libertad, el valor esperado es 0 si 1}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■1{displaystyle nu1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/67dc59709ea03ee8535240205566d3e844bd2b66" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/>, y su diferencia es .. .. − − 2{displaystyle {frac} ♫{nu -2}} si 2}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■2{displaystyle nu
2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/691ac5ce500a415f98d5eed0317f11e2a3b5f713" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/>. El juguetón es 0 si 3}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■3{displaystyle nu
3" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/901e92642c6e5e3632f6b8c7e3c6ed18a3d2695d" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/> y el exceso de kurtosis es 6.. − − 4{displaystyle {frac {6}{nu} -4}} si 4}" xmlns="http://www.w3.org/1998/Math/MathML">.. ■4{displaystyle nu >4}
4" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c74cec688bcbbcd1c01ace4dfc28b7769e2841cc" style="vertical-align: -0.338ex; width:5.493ex; height:2.176ex;"/>.
Muestreo de Montecarlo
Existen varios enfoques para construir muestras aleatorias a partir de la distribución t de Student. La cuestión depende de si las muestras se requieren de forma independiente o se van a construir mediante la aplicación de una función de cuantiles a muestras uniformes; por ejemplo, en la base de aplicaciones multidimensionales de la dependencia de la cópula. En el caso del muestreo independiente, se implementa fácilmente una extensión del método Box-Muller y su forma polar. Tiene el mérito de que se aplica igualmente bien a todos los grados de libertad reales positivos, ν, mientras que muchos otros métodos candidatos fallan si ν es cercano a cero.
Integral de la función de densidad de probabilidad de Student y valor p
La función A(t | ν) es la integral de la función de densidad de probabilidad de Student, f(t) entre −t y t, para t ≥ 0. Así da la probabilidad que un valor de t menor que el calculado a partir de los datos observados ocurriría por casualidad. Por lo tanto, la función A(t | ν) puede usarse cuando se prueba si la diferencia entre las medias de dos conjuntos de datos es estadísticamente significativa., calculando el valor correspondiente de t y la probabilidad de que ocurra si los dos conjuntos de datos se extrajeron de la misma población. Esto se usa en una variedad de situaciones, particularmente en pruebas t. Para el estadístico t, con ν grados de libertad, A(t | ν) es la probabilidad de que t sea menor que el valor observado si las dos medias fueran iguales (siempre que la media más pequeña se reste de la más grande, de modo que t ≥ 0). Se puede calcular fácilmente a partir de la función de distribución acumulada Fν(t) de la t-distribución:
- A()t▪ ▪ .. )=F.. ()t)− − F.. ()− − t)=1− − I.. .. +t2().. 2,12),{displaystyle A(tmid nu)=F_{nu }(t)-F_{nu }(-t)=1-I_{frac {nu }{nu ¿Qué?
donde Ix es la función beta incompleta regularizada (a, b).
Para las pruebas de hipótesis estadísticas, esta función se utiliza para construir el valor p.
Distribución t de Student generalizada
En términos del parámetro de escala σ̂ o σ̂2
La distribución t del estudiante se puede generalizar a una familia de escala de tres parámetros, introduciendo un parámetro de ubicación μ μ ^ ^ {displaystyle {hat {mu}}} y un parámetro de escala σ σ ^ ^ {displaystyle {hat {sigma} }, a través de la relación
- X=μ μ ^ ^ +σ σ ^ ^ T{displaystyle X={hat {mu }+{hat {sigma }T}
o
- T=X− − μ μ ^ ^ σ σ ^ ^ {displaystyle T={frac {X-{hat {mu}}{hat {sigma }
Esto significa que x− − μ μ ^ ^ σ σ ^ ^ {displaystyle {frac {x-{hat {mu}}{hat {sigma} } tiene una distribución t clásico Estudiante con .. {displaystyle nu } grados de libertad.
La distribución t- de Student no estandarizada resultante tiene una densidad definida por:
- p()x▪ ▪ .. ,μ μ ^ ^ ,σ σ ^ ^ )=.. ().. +12).. ().. 2)π π .. σ σ ^ ^ ()1+1.. ()x− − μ μ ^ ^ σ σ ^ ^ )2)− − ().. +1)/2{displaystyle p(xmid nu{hat {mu }},{hat {sigma }}={frac {Gamma ({frac {nu +1}{2}}}}{Gamma ({frac {nu }{2}}}}{sqrt {pinu }}{hat {sigma {sigma}}}}}} {sqrt {i}}}}}}} {f}}} { },}left(1+{frac {1}{nu }left({frac {x-{hat {mu }{hat {sigma ¿Qué?
Aquí, σ σ ^ ^ {displaystyle {hat {sigma} } ¿Sí? no corresponde a una desviación estándar: no es la desviación estándar de la escalada t distribución, que ni siquiera puede existir; ni es la desviación estándar de la distribución normal subyacente, que es desconocida. σ σ ^ ^ {displaystyle {hat {sigma} } simplemente establece el escalado general de la distribución. En la derivación bayesiana de la distribución marginal de un medio normal desconocido μ μ ^ ^ {displaystyle {hat {mu}}} arriba, σ σ ^ ^ {displaystyle {hat {sigma} } como se utiliza aquí corresponde a la cantidad s/n{displaystyle {s/{sqrt {}}, donde
- s2=.. ()xi− − x̄ ̄ )2n− − 1.{displaystyle {fn1}fn1}
Equivalentemente, la distribución se puede escribir en términos de σ σ ^ ^ 2{displaystyle {hat {sigma} } {2}, el cuadrado de este parámetro de escala:
- p()x▪ ▪ .. ,μ μ ^ ^ ,σ σ ^ ^ 2)=.. ().. +12).. ().. 2)π π .. σ σ ^ ^ 2()1+1.. ()x− − μ μ ^ ^ )2σ σ ^ ^ 2)− − ().. +1)/2{displaystyle p(xmid nu{hat {mu },{hat {sigma} }{2}={frac {Gamma ({frac {nu +1}{2}}}}{Gamma ({frac {nu }{2}}}}{sqrt {pinu {hat {sigma {fn} {fn} {fn} {fn} {fnfn} {fn}} {fn}}} {fn}} {fnfn}} {fn}} {fnfn}}} {fnfn}}}} {fnfnfnfnfnfnfn}}}}}}}}}}} {fn}}}}}}} {f}}}} {fnfnfnf}} {fnfn} {fnfn}}}}}}}}}}}}}} {fn} {fn}}}} {fn}} {fn}}}}} {fnfnfn} {fn}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}} {fn ¿Qué?
Otras propiedades de esta versión de la distribución son:
- 1\operatorname {var} (X)&={hat {sigma }}^{2}{frac {nu }{nu -2}}&{text{ for }}nu >2\operatorname {mode} (X)&={hat {mu }}end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">E ()X)=μ μ ^ ^ para.. ■1Var ()X)=σ σ ^ ^ 2.. .. − − 2para.. ■2modo ()X)=μ μ ^ ^ {displaystyle {begin{aligned}operatorname {E} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}\\\\\\\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnK} {fnK} {fnK}}fnK}}nu }nu }\\\\\\\\\\fnK} {fnMicrosoft}} {fnK}}fnK}}}}fnKfnK}}}}} {f}}}}}}fnun}}}fnun} {fnun}f}f}f}f}fnun}fnun}fnun}fnun}fnun}fnun}f}\\\\\fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}nun}fnun}fnun}fnun}nun}
1\operatorname {var} (X)&={hat {sigma }}^{2}{frac {nu }{nu -2}}&{text{ for }}nu >2\operatorname {mode} (X)&={hat {mu }}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e343cf78575ef09d0ebd09139a4ad8fca6ce9b8d" style="vertical-align: -4.751ex; margin-bottom: -0.254ex; width:35.603ex; height:11.176ex;"/>
Esta distribución resulta de la composición de una distribución Gaussiana (distribución normal) con media μ μ {displaystyle mu } y varianza desconocida, con una distribución gamma inversa colocada sobre la variabilidad con parámetros a=.. /2{displaystyle a=nu /2} y b=.. σ σ ^ ^ 2/2{displaystyle b=nu {sigma} } {2}/2}. En otras palabras, la variable aleatoria X se supone que tiene una distribución gaisiana con una varianza desconocida distribuida como gamma inversa, y luego la varianza está marginada (integrada). La razón de la utilidad de esta caracterización es que la distribución inversa gamma es la distribución previa conjugada de la varianza de una distribución gamma. Como resultado, el estudiante no estandarizado t- La distribución surge naturalmente en muchos problemas de inferencia Bayesiana. A continuación.
Equivalentemente, esta distribución resulta de la incorporación de una distribución Gausiana con una distribución escalada-inverso-chi-cuadrado con parámetros .. {displaystyle nu } y σ σ ^ ^ 2{displaystyle {hat {sigma} } {2}. La distribución escalada-inverse-chi-squared es exactamente la misma distribución que la distribución inversa gamma, pero con una parametrización diferente, es decir,. .. =2a,σ σ ^ ^ 2=ba{displaystyle nu =2a,;{hat {sigma }{2}={frac {b}{a}}.
Esta versión de la distribución t puede ser útil en el modelado financiero. Por ejemplo, Platen y Sidorowicz descubrieron que entre la familia de distribuciones hiperbólicas generalizadas, esta forma de distribución t con aproximadamente 4 grados de libertad era la que mejor se ajustaba al rendimiento (logarítmico) de muchos índices bursátiles mundiales.
En términos del parámetro de escala inversa λ
Una parametrización alternativa en términos de un parámetro inverso de escalado λ λ {displaystyle lambda } (análogamente a la forma en que la precisión es la reciproca de la varianza), definida por la relación λ λ =1σ σ ^ ^ 2{displaystyle lambda ={frac {1}{hat {sigma} } {2}},}. La densidad es entonces dada por:
- p()x▪ ▪ .. ,μ μ ^ ^ ,λ λ )=.. ().. +12).. ().. 2)()λ λ π π .. )1/2()1+λ λ ()x− − μ μ ^ ^ )2.. )− − ().. +1)/2.{displaystyle p(xmid nu{hat {mu }},lambda)={frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}} {fnMicros {c} {fnMicrosoft} {fnMicrosoft Sans Serif}}} {fnMicros} {fnMicroc} {fnMicrosoft}} {f} {f}f}}}}}fnun} {fnun}}fnun}f}}}fnun}}fnun}}fnun}}fnun}}}fnun}fnun}fnun}}fnun}fnun}fnun}}fnun}}fnun}fnun}fnun}fnun} {fnun} {fnun} {fnun} {fnunfnun}fnun} {fnun}
Otras propiedades de esta versión de la distribución son:
- 1\[5pt]operatorname {var} (X)&={frac {1}{lambda }}{frac {nu }{nu -2}}&&{text{ for }}nu >2\[5pt]operatorname {mode} (X)&={hat {mu }}end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">E ()X)=μ μ ^ ^ para.. ■1Var ()X)=1λ λ .. .. − − 2para.. ■2modo ()X)=μ μ ^ ^ {displaystyle {begin{aligned}operatorname {E} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {1}{fn0}{fn0} {fn0} {fn0} {fnMicrosoft}}} {fnun} {fnun}}fnMicrox}}}fnun}}fnun} {fnun}fnfnun}fnun}fnun}fnun}fnKfnun}fnfnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun} {fnMicroc {nu} {nu} {fn0}nu }nu }n0[5pt]operatorname {mode} (X) ventaja={hat {mu }end{aligned}}
1\[5pt]operatorname {var} (X)&={frac {1}{lambda }}{frac {nu }{nu -2}}&&{text{ for }}nu >2\[5pt]operatorname {mode} (X)&={hat {mu }}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5d718430b8350f0ada28d216c96d8944e72d7e2a" style="vertical-align: -6.505ex; width:35.41ex; height:14.176ex;"/>
Esta distribución resulta de la composición de una distribución Gausiana con media μ μ ^ ^ {displaystyle {hat {mu}}} y precisión desconocida (la reciproca de la varianza), con una distribución gamma colocada sobre la precisión con parámetros a=.. /2{displaystyle a=nu /2} y b=.. /()2λ λ ){displaystyle b=nu /(2lambda)}. En otras palabras, la variable aleatoria X se supone que tiene una distribución normal con una precisión desconocida distribuida como gamma, y entonces esto se margina sobre la distribución gamma.
Distribuciones relacionadas
- Si X{displaystyle X} tiene un estudiante t-distribución con grado de libertad .. {displaystyle nu } entonces X2 tiene una F-distribución: X2♪ ♪ F().. 1=1,.. 2=.. ){displaystyle X^{2}sim mathrm {F} left(nu _{1}=1,nu _{2}=nu right)}
- La distribución t no central generaliza la t-Distribución para incluir un parámetro de ubicación. A diferencia de los no estandarizados t-distribuciones, las distribuciones no centrales no son simétricas (el medio no es el mismo que el modo).
- El discreto Estudiante t-distribución se define por su función de masa de probabilidad en r ser proporcional a: Aquí. a, b, y k son parámetros. Esta distribución surge de la construcción de un sistema de distribuciones discretas similares a la de las distribuciones Pearson para distribuciones continuas.∏ ∏ j=1k1()r+j+a)2+b2r=...... ,− − 1,0,1,...... .{displaystyle prod _{j=1}{k}{frac {1}{2}quad quad r=ldots-1,0,1,ldots.}
- Uno puede generar Student-t muestra tomando la relación de variables de la distribución normal y la raíz cuadrada χ2-distribución. Si utilizamos en lugar de la distribución normal, por ejemplo, la distribución Irwin-Hall, obtenemos sobre todo una distribución simétrica de 4 parámetros, que incluye lo normal, el uniforme, el triangular, el Student-t y la distribución Cauchy. Esto también es más flexible que otras generalizaciones simétricas de la distribución normal.
- t- La distribución es un ejemplo de distribución de ratios.
Inferencia bayesiana: distribución previa para los grados de libertad
Supongamos que x=()x1,⋯ ⋯ ,xN){displaystyle x=(x_{1},cdotsx_{N}} representaciones N{displaystyle N} Número de muestras distribuidas de forma independiente e idéntica extraídas del Student t-distribution
t.. ()x)=.. ().. +12).. π π .. ().. 2)()1+x2.. )− − .. +12,x▪ ▪ R.{displaystyle t_{nu }(x)={frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {nMicrosoft Sans Serif} {fnMicrosoft Sans Serif} pi }Gammaleft({frac {nu }{2}right)}left(1+{frac {x^{2}{nu }}right)}{-{frac {nu +1}{2}}}}quad xin mathbb {R}.}
Con una elección previa para los grados de libertad .. {displaystyle nu }, denotado como π π ().. ){displaystyle pi (nu)}, Inferencia Bayesiana busca evaluar la distribución posterior
π π ().. Silenciox)=∏ ∏ t.. ()xi)⋅ ⋅ π π ().. )∫ ∫ ∏ ∏ t.. ()xi)⋅ ⋅ π π ().. )d.. ,.. ▪ ▪ R+.{displaystyle pi (nu Silencio{textbf {x})={frac {prod t_{nu }(x_{i})cdot pi (nu)}{int prod t_{nu }(x_{i})cdot pi (nu)dnu },quad nu [R] ^{+}

Algunas opciones populares de los anteriores son:
- Jeffreys prior
π π J().. )∝ ∝ ().. .. +3)1/2()↑ ↑ .().. 2)− − ↑ ↑ .().. +12)− − 2().. +3).. ().. +1)2)1/2,.. ▪ ▪ R+,{nMicrosoft Sans Serif} {nMicrosoft Sans Serif} {nMicrosoft Sans Serif} {nMicrosoft Sans Serif}Donde ↑ ↑ .()x){displaystyle psi '(x)} representa la función trigamma.
- Exponential prior
π π E().. )=Ga().. Silencio1,0.1)=exp ().. Silencio0.1)=110e− − .. /10,.. ▪ ▪ R+{displaystyle pi _{E}(nu)=Ga(nu TEN1,0.1)=exp(nu TEN0.1)={frac {1}{10}}e^{-nu /10},quad nu in mathbbbb {R} {fn}
- Gamma prior
π π G().. )=Ga().. Silencio2,0.1)=.. 100e− − .. /10,.. ▪ ▪ R+{displaystyle pi _{G}(nu)=Ga(nu tención2,0.1)={frac {nu }{100}e^{-nu /10},quad nu in mathbb {R} {fn}
- Log-normal prior
π π L().. )=logN().. Silencio1,1)=1.. 2π π exp [− − ()log .. − − 1)22],.. ▪ ▪ R+{displaystyle pi _{L}(nu)=logN(nu Н1,1)={frac {1}{nu {sqrt {2pi}}}}expleft[-{frac {log nu -1)^{2}}}right],quad nu in mathbb {R} {fn}
Los paneles adecuados muestran el resultado de los experimentos numéricos. El estimador de Bayes basado en los Jeffreys anteriores π π J().. ){displaystyle pi _{J}(nu)} resultados en el Error Mean Squared relativamente menor (MSE) entonces el Estimador de la probabilidad máxima (MLE) sobre los valores .. 0▪ ▪ ()0,25){displaystyle nu _{0}in (0,25)}. Es importante señalar que ningún estimador de Bayes domina a otros estimadores a lo largo del intervalo ()0,25){displaystyle (0,25)}. En otras palabras, cada estimador de Bayes tiene su propia región donde el estimador no es inferior para otros.
Usos
En la inferencia estadística frecuentista
La distribución t de Student surge en una variedad de problemas de estimación estadística donde el objetivo es estimar un parámetro desconocido, como un valor medio, en un entorno donde se observan los datos con errores aditivos. Si (como en casi todos los trabajos estadísticos prácticos) se desconoce la desviación estándar de la población de estos errores y se debe estimar a partir de los datos, la distribución t se usa a menudo para tener en cuenta la incertidumbre adicional que resulta de esta estimación. En la mayoría de estos problemas, si se conociera la desviación estándar de los errores, se usaría una distribución normal en lugar de la distribución t.
Los intervalos de confianza y las pruebas de hipótesis son dos procedimientos estadísticos en los que se requieren los cuantiles de la distribución muestral de una estadística en particular (por ejemplo, la puntuación estándar). En cualquier situación en la que esta estadística sea una función lineal de los datos, dividida por la estimación habitual de la desviación estándar, la cantidad resultante se puede reescalar y centrar para seguir la distribución t de Student. Los análisis estadísticos que involucran medias, medias ponderadas y coeficientes de regresión conducen a estadísticas que tienen esta forma.
Muy a menudo, los problemas de los libros de texto tratarán la desviación estándar de la población como si fuera conocida y, por lo tanto, evitarán la necesidad de utilizar la distribución t de Student. Estos problemas son generalmente de dos tipos: (1) aquellos en los que el tamaño de la muestra es tan grande que se puede tratar una estimación de la varianza basada en datos como si fuera cierta, y (2) aquellos que ilustran el razonamiento matemático, en los que el problema de estimar la desviación estándar se ignora temporalmente porque ese no es el punto que el autor o el instructor está explicando.
Prueba de hipótesis
Se puede demostrar que varias estadísticas tienen distribuciones t para muestras de tamaño moderado bajo hipótesis nulas que son de interés, de modo que la distribución t forma la base para las pruebas de significación. Por ejemplo, la distribución del coeficiente de correlación de rangos de Spearman ρ, en el caso nulo (correlación cero) se aproxima bien mediante la distribución t para tamaños de muestra superiores a 20
Intervalos de confianza
Suponga que el número A se elige de tal manera que
- <math alttext="{displaystyle Pr(-A<TPr()− − A.T.A)=0.9,{displaystyle Pr(-A obtenidosA)=0.9,}<img alt="Pr(-A < T
cuando T tiene una distribución t con n − 1 grados de libertad. Por simetría, esto es lo mismo que decir que A satisface
- <math alttext="{displaystyle Pr(TPr()T.A)=0.95,{displaystyle Pr(T wonA)=0.95,}<img alt="Pr(T
Así que... A es el percentil 95 de esta distribución de probabilidad, o A=t()0,05,n− − 1){displaystyle A=t_{(0.05,n-1)}. Entonces...
- <math alttext="{displaystyle Pr left(-A<{frac {{overline {X}}_{n}-mu }{S_{n}/{sqrt {n}}}}Pr()− − A.X̄ ̄ n− − μ μ Sn/n.A)=0.9,{displaystyle Pr left {fnMicrosoft Sans Serif} {X}_{n}-mu} ♫ {S_{n}/{sqrt {n}} {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn}}}}} {fn}}}}}<img alt="{displaystyle Pr left(-A<{frac {{overline {X}}_{n}-mu }{S_{n}/{sqrt {n}}}}
y esto es equivalente a
- <math alttext="{displaystyle Pr left({overline {X}}_{n}-A{frac {S_{n}}{sqrt {n}}}<mu Pr()X̄ ̄ n− − ASnn.μ μ .X̄ ̄ n+ASnn)=0.9.{displaystyle Pr left({overline {X}_{n}-A{frac {fn} {fn} {fn}} {fn} {fn}} {fn}} {fn}}} {fn}}}}}} {fn} {fn} {fn} {fn}}} {fn}}}}}}}}} {\fn}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\fn} {fn}}}}\\\\\\\\\\\\\\fn} {n}fn} {\fn}n}\\\fn} {\\fn}}\\\\\\\\\\\\\\\\\ {S_{n}{sqrt {n}}right)=0.9}<img alt="Prleft(overline{X}_n - A frac{S_n}{sqrt{n}} < mu
Por lo tanto, el intervalo cuyos extremos son
- X̄ ̄ n± ± ASnn{displaystyle {fn}_{n}pm ¿Qué?
es un intervalo de confianza del 90 % para μ. Por lo tanto, si encontramos la media de un conjunto de observaciones que razonablemente podemos esperar que tengan una distribución normal, podemos usar la distribución t para examinar si los límites de confianza en esa media incluyen algunos valores predichos teóricamente. valor – como el valor predicho en una hipótesis nula.
Es este resultado el que se usa en las pruebas t de Student: dado que la diferencia entre las medias de las muestras de dos distribuciones normales se distribuye normalmente, la distribución t puede utilizarse para examinar si se puede suponer razonablemente que esa diferencia es cero.
Si los datos se distribuyen normalmente, el límite de confianza superior (UCL) unilateral (1 − α) de la media se puede calcular mediante la siguiente ecuación:
- UCL1− − α α =X̄ ̄ n+tα α ,n− − 1Snn.{displaystyle mathrm {UCL} _{1-alpha }={overline {X}_{n}+t_{alphan-1}{frac {S_{n} { sqrt {n}}} {fn}} {fn}} {fn}} {fn}} {fn}}}} {fn}}} {fn}}}} {fn}}}} {fn}}}}}}} {cHFF}}}}}}}} {cc\\cHFF}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {cc\\cccccccccccc\ccHFF}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
El UCL resultante será el mayor valor promedio que ocurrirá para un intervalo de confianza dado y tamaño de la población. En otras palabras, X̄ ̄ n{displaystyle {fnK} {fn} {fn}} {fn}}} {fn}}}} {fn}}} {fn}}}}}} {fn}}}}}}} {fn}}}}}}}} {fn}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { siendo la media del conjunto de observaciones, la probabilidad de que la media de la distribución sea inferior a la UCL1 - 1α es igual al nivel de confianza 1 − α.
Intervalos de predicción
La distribución t se puede utilizar para construir un intervalo de predicción para una muestra no observada de una distribución normal con media y varianza desconocidas.
En estadísticas bayesianas
La distribución t de Student, especialmente en su versión de tres parámetros (ubicación-escala), surge con frecuencia en las estadísticas bayesianas como resultado de su conexión con la distribución normal. Siempre que se desconozca la varianza de una variable aleatoria con distribución normal y se le coloque un previo conjugado que siga una distribución gamma inversa, la distribución marginal resultante de la variable seguirá una distribución t de Student.. Las construcciones equivalentes con los mismos resultados implican una distribución de chi-cuadrado inversa escalada conjugada sobre la varianza, o una distribución gamma conjugada sobre la precisión. Si sobre la varianza se coloca un anterior impropio proporcional a σ−2, también surge la distribución t. Este es el caso independientemente de si se conoce la media de la variable con distribución normal, se desconoce la distribución de acuerdo con una distribución previa conjugada normal o se desconoce la distribución de acuerdo con una constante previa impropia.
Las situaciones relacionadas que también producen una distribución t son:
- La distribución posterior marginal de la media desconocida de una variable normalmente distribuida, con media y varianza previa desconocida siguiendo el modelo anterior.
- La distribución predictiva previa y posterior distribución predictiva de un nuevo punto de datos normalmente distribuido cuando se ha observado una serie de puntos de datos distribuidos de forma idéntica, con media y varianza previas como en el modelo anterior.
Modelado paramétrico robusto
La distribución t se usa a menudo como una alternativa a la distribución normal como modelo para los datos, que a menudo tiene colas más pesadas de lo que permite la distribución normal; ver por ej. Lange et al. El enfoque clásico consistía en identificar valores atípicos (p. ej., utilizando la prueba de Grubbs) y excluirlos o reducir su peso de alguna manera. Sin embargo, no siempre es fácil identificar valores atípicos (especialmente en dimensiones altas), y la distribución t es una elección natural de modelo para tales datos y proporciona un enfoque paramétrico para estadísticas sólidas.
Se puede encontrar una cuenta bayesiana en Gelman et al. El parámetro de grados de libertad controla la curtosis de la distribución y está correlacionado con el parámetro de escala. La verosimilitud puede tener múltiples máximos locales y, como tal, a menudo es necesario fijar los grados de libertad en un valor bastante bajo y estimar los otros parámetros tomando esto como dado. Algunos autores informan que los valores entre 3 y 9 suelen ser buenas opciones. Venables y Ripley sugieren que un valor de 5 suele ser una buena elección.
Proceso t de la estudiante
(feminine)Para necesidades prácticas de regresión y predicción, Estudiante t-procesos fueron introducidos, que son generalizaciones del Estudiante t-distribuciones para funciones. Un estudiante t- el proceso se construye desde el estudiante t-distribuciones como un proceso gausiano se construyen a partir de las distribuciones gausianas. Para un proceso gaussiano, todos los conjuntos de valores tienen una distribución gaissiana multidimensional. Analógicamente, X()t){displaystyle X(t)} es un estudiante t-proceso en un intervalo I=[a,b]{displaystyle I=[a,b] si los valores corresponsales del proceso X()t1),...,X()tn){displaystyle X(t_{1}),...,X(t_{n} ()ti▪ ▪ I{displaystyle t_{i}in Yo...) tienen un estudiante multivariado conjunto t-distribución. Estos procesos se utilizan para regresión, predicción, optimización bayesiana y problemas relacionados. Para la regresión multivariada y la predicción multi-output, el estudiante multivariable t- se introducen y usan los procedimientos.
Tabla de valores seleccionados
Los valores de las tablas siguientes t-distribuciones con . grados de libertad para una serie de regiones críticas unilaterales o de dos caras. La primera columna es ., los porcentajes a lo largo de la parte superior son niveles de confianza, y los números en el cuerpo de la tabla son los tα α ,n− − 1{displaystyle t_{alphan-1} factores descritos en la sección sobre intervalos de confianza.
La última fila con infinitos ν da puntos críticos para una distribución normal ya que una distribución t con infinitos grados de libertad es una distribución normal. (Consulte Distribuciones relacionadas más arriba).
| Un lado | 75% | 80% | 85% | 90% | 95% | 97,5% | 99% | 99,5% | 99,75% | 99,9% | 99,95% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dos caras | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99,5% | 99,8% | 99,9% |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 | 127.321 | 318.309 | 636.619 |
| 2 | 0.816 | 1.080 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.089 | 22.327 | 31.599 |
| 3 | 0,7565 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.215 | 12.924 |
| 4 | 0,7441 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0,2727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0,7818 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0,7500 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0,870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0,6989 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0,6787 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0,6979 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0,6979 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0,678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
| JUEGO | 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
| Un lado | 75% | 80% | 85% | 90% | 95% | 97,5% | 99% | 99,5% | 99,75% | 99,9% | 99,95% |
| Dos caras | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99,5% | 99,8% | 99,9% |
Cálculo del intervalo de confianza
Digamos que tenemos una muestra con tamaño 11, media muestral 10 y varianza muestral 2. Para un 90 % de confianza con 10 grados de libertad, el valor t unilateral de la tabla es 1.372. Luego, con el intervalo de confianza calculado a partir de
- X̄ ̄ n± ± tα α ,.. Snn,{displaystyle {fn}_{n}pm t_{alphanu }{frac {S_{n}{sqrt {n}}} {fn}} {fn}} {fn}} {fn}}} {fn}}}}} {fn}}}}}} {fn}}}}}} {fn}}}}}}}} {fn}}}}}}}}}}} {
determinamos que con un 90 % de confianza tenemos una media verdadera debajo
- 10+1.372211=10.585.{displaystyle 10+1.372{sqrt {2}}=10.585.}
En otras palabras, el 90 % de las veces que se calcula un umbral superior mediante este método a partir de muestras particulares, este umbral superior supera la media real.
Y con un 90 % de confianza, tenemos una media verdadera por encima
- 10− − 1.372211=9.414.{displaystyle 10-1.372{sqrt {2}}=9.414.}
En otras palabras, el 90 % de las veces que se calcula un umbral inferior mediante este método a partir de muestras particulares, este umbral inferior se encuentra por debajo de la media real.
De modo que con un 80 % de confianza (calculado a partir de 100 % − 2 × (1 − 90 %) = 80 %), tenemos una media verdadera dentro del intervalo
- ()10− − 1.372211,10+1.372211)=()9.414,10.585).{displaystyle left(10-1.372{frac {sqrt {2}{sqrt {11}}},10+1.372{frac {sqrt {2}{sqrt {11}}}right)=(9.414,10.585).}
Decir que el 80 % de las veces que los umbrales superior e inferior se calculan mediante este método a partir de una muestra dada, la verdadera media está tanto por debajo del umbral superior como por encima del umbral inferior no es lo mismo que decir que hay un 80 % de probabilidad de que la verdadera media se encuentre entre un par particular de umbrales superior e inferior que han sido calculados por este método; ver intervalo de confianza y falacia del fiscal.
Hoy en día, el software estadístico, como el lenguaje de programación R, y las funciones disponibles en muchos programas de hojas de cálculo calculan los valores de la distribución t y su inversa sin tablas.
Contenido relacionado
Cepstrum
Factorial
Logaritmo discreto










































![{displaystyle {frac {1}{2}}+{frac {1}{pi }}{left[{frac {1}{sqrt {3}}}{frac {t}{1+{frac {t^{2}}{3}}}}+arctan left({frac {t}{sqrt {3}}}right)right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0afffc07f0c86a59eaa560dc8a3cf8f6fa83ccd)

![{displaystyle {frac {1}{2}}+{frac {3}{8}}{frac {t}{sqrt {1+{frac {t^{2}}{4}}}}}{left[1-{frac {1}{12}}{frac {t^{2}}{1+{frac {t^{2}}{4}}}}right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8267697404a72109b22e9add73ef7023d1953235)

![{displaystyle {frac {1}{2}}+{frac {1}{pi }}{left[{frac {t}{{sqrt {5}}left(1+{frac {t^{2}}{5}}right)}}left(1+{frac {2}{3left(1+{frac {t^{2}}{5}}right)}}right)+arctan left({frac {t}{sqrt {5}}}right)right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeef99bb2df092bdcc8c708cbc0c29cfe1849232)


![{displaystyle {frac {1}{2}}{left[1+operatorname {erf} left({frac {t}{sqrt {2}}}right)right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e86c11ecfcdc01d2a24c4afd9b4e0e0a4aff6424)

![{displaystyle {begin{aligned}{bar {x}}&={frac {x_{1}+cdots +x_{n}}{n}},\[5pt]s^{2}&={frac {1}{n-1}}sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b254594b738c8226106dced8dcc81c7f7c4d2ae)































































![{displaystyle pi _{L}(nu)=logN(nu |1,1)={frac {1}{nu {sqrt {2pi }}}}exp left[-{frac {(log nu -1)^{2}}{2}}right],quad nu in mathbb {R} ^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2286de11b6b2ca854ad197e07212694e467d1dea)







![I=[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6214bb3ce7f00e496c0706edd1464ac60b73b5)






