Distribución normal multivariante

En teoría de probabilidad y estadística, la distribución normal multivariante, distribución gaussiana multivariante o distribución normal conjunta es una generalización de la distribución normal dimensional (univariada) a dimensiones superiores. Una definición es que se dice que un vector aleatorio tiene una distribución normal variable k si cada combinación lineal de sus componentes k tiene una distribución normal univariante. Su importancia se deriva principalmente del teorema del límite central multivariante. La distribución normal multivariante se usa a menudo para describir, al menos aproximadamente, cualquier conjunto de variables aleatorias de valor real (posiblemente) correlacionadas, cada una de las cuales se agrupa alrededor de un valor medio.

Definiciones

Notación y parametrización

La distribución normal multivariada de un k-dimensional vector aleatorio ${displaystyle mathbf {X} =(X_{1},ldotsX_{k}{mathrm {T}}$ se puede escribir en la siguiente notación:

${displaystyle mathbf {X} \sim {mathcal {N}({boldsymbol {mu }},,{boldsymbol {Sigma }}}}}}$

o para hacer saber explícitamente que X es k-dimensional,

${displaystyle mathbf {X} \sim {n}_{k}({boldsymbol {mu }},,{boldsymbol {sigma}}}}}}}}$

con vector medio k-dimensional

${displaystyle {boldsymbol {mu} ##=operatorname {E} [mathbf {X}=operatorname [E] [X_{1},operatorname {E} [X_{2},ldotsoperatorname {E} [X_{k}]} {textbf {T}}}$

y ${displaystyle ktimes k}$ matriz de covariancia

${displaystyle Sigma _{i,j}=operatorname {E} [(X_{i}-mu _{i})(X_{j}-mu _{j})=operatorname {Cov} [X_{i},X_{j}}$

tales que ${displaystyle 1leq ileq k}$ y ${displaystyle 1leq jleq k}$. El inverso de la matriz de covariancia se llama la matriz de precisión, denotada por ${displaystyle {boldsymbol {Q}={boldsymbol {Sigma}}} {-1}$.

Vector aleatorio normal estándar

Un vector aleatorio real ${displaystyle mathbf {X} =(X_{1},ldotsX_{k}{mathrm {T}}$ se llama vector normal aleatorio normal si todos sus componentes ${displaystyle X_{i}$ son independientes y cada una es una unidad-varianza cero-medio normalmente distribuida variable aleatoria, es decir, si ${displaystyle X_{i}sim {fn}(0,1)}$ para todos ${displaystyle i=1ldots k}$.

Vector aleatorio normal centrado

Un vector aleatorio real ${displaystyle mathbf {X} =(X_{1},ldotsX_{k}{mathrm {T}}$ se llama centrado normal vector aleatorio si existe un determinista ${displaystyle ktimes ell }$ matriz ${displaystyle {boldsymbol {A}}$ tales que ${displaystyle {fncipulo}mátbf {Z}$ tiene la misma distribución ${displaystyle mathbf {X}$ Donde ${displaystyle mathbf {Z}$ es un vector normal aleatorio normal con ${displaystyle ell }$ componentes.

Vector aleatorio normal

Un vector aleatorio real ${displaystyle mathbf {X} =(X_{1},ldotsX_{k}{mathrm {T}}$ se llama vector aleatorio normal si existe un azar ${displaystyle ell }$-vector ${displaystyle mathbf {Z}$, que es un vector normal normal al azar, un ${displaystyle k}$-vector ${displaystyle mathbf {mu}$, y un ${displaystyle ktimes ell }$ matriz ${displaystyle {boldsymbol {A}}$, tal que ${displaystyle mathbf {X} ={boldsymbol Mathbf...$.

Formalmente:

Aquí está la matriz de covariancia ${displaystyle {boldsymbol {Sigma }={boldsymbol {A}{boldsymbol {} {fn} {fnK}} {fnK}}}} {fnK}}}} {fn}}} {fn}}}}} {fn}}}}}}}}}}} {fn}}}}}}}}}} {\fnK}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\$.

En el caso degenerado donde la matriz de covariancia es singular, la distribución correspondiente no tiene densidad; vea la sección abajo para detalles. Este caso surge con frecuencia en las estadísticas; por ejemplo, en la distribución del vector de residuos en la regresión de los mínimos cuadrados ordinarios. El ${displaystyle X_{i}$ en general no independiente; pueden verse como el resultado de la aplicación de la matriz ${displaystyle {boldsymbol {A}}$ a una colección de variables gaisianas independientes ${displaystyle mathbf {Z}$.

Definiciones equivalentes

Las siguientes definiciones son equivalentes a la definición dada anteriormente. Un vector aleatorio ${displaystyle mathbf {X} =(X_{1},ldotsX_{k} {T}}$ tiene una distribución normal multivariada si satisface una de las siguientes condiciones equivalentes.

• Cada combinación lineal ${displaystyle Y=a_{1}X_{1}+cdots - ¿Qué?$ de sus componentes se distribuye normalmente. Es decir, para cualquier vector constante ${displaystyle mathbf {a} in mathbb {R} ^{k}$, la variable aleatoria ${displaystyle Y=Mathbf {a} {T} 'Mathbf {X}$ tiene una distribución normal univariada, donde una distribución normal univariada con varianza cero es una masa de punto en su media.
• Hay un k-vector ${displaystyle mathbf {mu}$ y un semidefinido positivo simétrico ${displaystyle ktimes k}$ matriz ${displaystyle {boldsymbol {Sigma }$, tal que la función característica de ${displaystyle mathbf {X}$ es
  $${displaystyle varphi _{mathbf {X}(mathbf {u})=exp {Big (}imathbf {u} }{T}{boldsymbol {mu}-{tfrac {1}{2}mathbf {u} ^{T}{boldsymbol Mathbf.$$

  

La distribución normal esférica se puede caracterizar como la distribución única donde los componentes son independientes en cualquier sistema de coordenadas ortogonales.

Función de densidad

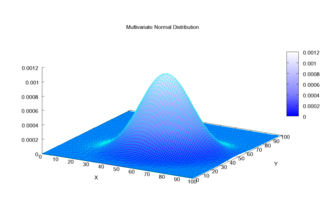
Densidad bivariable de articulación normal

Caso no degenerado

Se dice que la distribución normal multivariada es "no degenerada" cuando la matriz de covariancia simétrica ${displaystyle {boldsymbol {Sigma }$ es positivo. En este caso la distribución tiene densidad

Donde ${displaystyle {mathbf {x}}$ es un verdadero k-dimensional vector de columna y ${equivequiv det {boldsymbol {Sigma} {Sigma }$ es el determinante ${displaystyle {boldsymbol {Sigma }$, también conocido como la varianza generalizada. La ecuación anterior reduce a la de la distribución normal univariada si ${displaystyle {boldsymbol {Sigma }$ es un ${displaystyle 1times 1}$ matriz (es decir, un número real único).

La versión circularmente simétrica de la distribución normal compleja tiene una forma ligeramente diferente.

Cada lugar geométrico de iso-densidad, el lugar geométrico de los puntos en el espacio k-dimensional, cada uno de los cuales da el mismo valor particular de la densidad, es una elipse o su generalización de dimensión superior; por tanto, la normal multivariante es un caso especial de las distribuciones elípticas.

La cantidad ${fnMicrosoft} ¿Qué? {Sigma} {fnMitbf {x} }$ se conoce como la distancia Mahalanobis, que representa la distancia del punto de prueba ${displaystyle {mathbf {x}}$ de la media ${displaystyle {boldsymbol {mu}}$. Note que en el caso cuando ${displaystyle k=1}$, la distribución reduce a una distribución normal univariada y la distancia Mahalanobis reduce al valor absoluto de la puntuación estándar. Vea también Intervalo abajo.

Caso bivariado

En el caso no singular 2-dimensional${displaystyle k=operatorname {rank} left(Sigma right)=2}$), la función de densidad de probabilidad de un vector ${displaystyle {text{[XY]}}}$ es:

$${displaystyle f(x,y)={frac {1}{2pi sigma _{X}sigma ¿Qué? {1-rho ^{2}}}exp left(-{frac {1}{2(1-rho ^{2}}}}left[left({fracfrac {x-mu ¿Qué? ¿Por qué? ¿Qué? ¿Qué? ¿Qué? ¿Por qué? - Sí.$$

${displaystyle rho }$

${displaystyle X}$

${displaystyle Sí.$

${displaystyle sigma _{X} confianza0}$

${displaystyle sigma _{Y}conocido0}$

${displaystyle {boldsymbol {mu} }={begin{pmatrix}mu ¿Por qué? ¿Por qué? {Sigma # {begin{pmatrix}sigma ################################################################################################################################################################################################################################################################ _{X}sigma ¿Por qué? _{X}sigma ################################################################################################################################################################################################################################################################ ¿Qué?$

En el caso bivariado, la primera condición equivalente para la reconstrucción multivariada de la normalidad puede ser menos restrictiva ya que es suficiente para verificar que contablemente muchas combinaciones lineales distintas de ${displaystyle X}$ y ${displaystyle Sí.$ son normales para concluir que el vector de ${displaystyle {text{[XY]}}}$ es bivariable normal.

El loci iso-densidad bivariada trazado en el ${displaystyle x,y}$-plano son elipses, cuyos ejes principales son definidos por los eigenvectores de la matriz de covariancia ${displaystyle {boldsymbol {Sigma }$ (los semidiámetros mayores y menores de la elipse igualan la raíz cuadrada de los eigenvalues ordenados).

Distribución normal bivariada centrada en ${displaystyle (1,3)}$ con una desviación estándar de 3 en aproximadamente el ${displaystyle (0.878,0.478)}$ dirección y de 1 en dirección ortogonal.

Como valor absoluto del parámetro de correlación ${displaystyle rho }$ aumenta, estos loci se exprimen hacia la siguiente línea:

${displaystyle y(x)=operatorname {sgn}(rho){frac {sigma ¿Qué? ¿Qué?$

Esto es porque esta expresión, con ${displaystyle operatorname {sgn}(rho)}$ (donde sgn es la función Sign) sustituido por ${displaystyle rho }$, es la mejor predicción lineal imparcial de ${displaystyle Sí.$ dado un valor ${displaystyle X}$.

Caso degenerado

Si la matriz de covariancia ${displaystyle {boldsymbol {Sigma }$ no es de rango completo, entonces la distribución normal multivariada es degenerada y no tiene una densidad. Más precisamente, no tiene una densidad con respecto a k-dimensional Medida de Lebesgue (que es la medida habitual asumida en los cursos de probabilidad de nivel de cálculo). Sólo vectores aleatorios cuyas distribuciones son absolutamente continuas con respecto a una medida se dice que tienen densidades (con respecto a esa medida). Para hablar de densidades pero evitar tratar con complicaciones teoréticas de medida puede ser más simple restringir la atención a un subconjunto de ${displaystyle operatorname {rank} {boldsymbol {Sigma}}}}}$ de las coordenadas ${displaystyle mathbf {x}$ tal que la matriz de covariancia para este subconjunto es positiva definida; entonces las otras coordenadas pueden ser consideradas como una función afinada de estas coordenadas seleccionadas.

Para hablar de densidades significativamente en casos singulares, debemos seleccionar una medida de base diferente. Usando el teorema de desintegración podemos definir una restricción de la medida de Lebesgue a la ${displaystyle operatorname {rank} {boldsymbol {Sigma}}}}}$- subespacial affine dimensional ${displaystyle mathbb {R} {cH00}$ donde se apoya la distribución gaussiana, es decir, ${displaystyle ################################################################################################################################################################################################################################################################ }+{boldsymbol {Sigma Mathbf {v}$. Con respecto a esta medida la distribución tiene la densidad del motivo siguiente:

${displaystyle f(mathbf {x})={frac {e^{-{frac {1}{2}} {mathbf {x}} - ¡Oh, Dios mío! {Sigma}}} {mátbf {x} -{boldsym {mu}}}}{sqrt {(2pi)}det nolimits ^{*}({boldsymbol {Sigma}}}}}}$

Donde ${displaystyle {boldsymbol {Sigma}}} {+}}$ es el inverso generalizado, ${displaystyle k}$ es el rango de ${displaystyle {boldsymbol {Sigma }$ y ${displaystyle det nolimits ^{*}$ es el pseudo-determinante.

Función de distribución acumulativa

La noción de función de distribución acumulativa (cdf) en la dimensión 1 se puede extender de dos maneras al caso multidimensional, basado en regiones rectangulares y elipsoidales.

La primera manera es definir el cdf ${displaystyle F(mathbf {x})}$ de un vector aleatorio ${displaystyle mathbf {X}$ como la probabilidad de que todos los componentes ${displaystyle mathbf {X}$ son inferiores o iguales a los valores correspondientes en el vector ${displaystyle mathbf {x}$:

${fnMitbf {x}=mthbb {P} (mathbf {X} leq mathbf {x}),quad {text{where }mathbf {X}sim {mathcal {} {m} {m} {m} {cH00FF}cH00}cH00}cH00}cH00}$

Aunque no hay forma cerrada para ${displaystyle F(mathbf {x})}$, hay un número de algoritmos que lo estiman numéricamente.

Otra manera es definir el cdf ${displaystyle F(r)}$ como la probabilidad de que una muestra se encuentra dentro del ellipsoide determinado por su distancia Mahalanobis ${displaystyle r}$ del Gaussian, una generalización directa de la desviación estándar. Para calcular los valores de esta función, existen fórmulas analíticas cerradas, como sigue.

Intervalo

El intervalo para la distribución normal multivariante produce una región que consta de esos vectores x que satisfacen

${displaystyle ({mathbf {x}-{boldsymbol {mu })}{T}{boldsymbol {Sigma }} {máthbf {x}-{boldsymbol {mu })leq chi _{k}{2}(p). }$

Aquí. ${displaystyle {mathbf {x}}$ es un ${displaystyle k}$- vector dimensional, ${displaystyle {boldsymbol {mu}}$ es el conocido ${displaystyle k}$- vector medio dimensional, ${displaystyle {boldsymbol {Sigma }$ es la matriz de covariancia conocida y ${displaystyle chi _{k}{2}(p)}$ es la función cuantil para la probabilidad ${displaystyle p}$ de la distribución de chi-squared con ${displaystyle k}$ grados de libertad. Cuando ${displaystyle k=2,}$ la expresión define el interior de una elipse y la distribución equiparada simplifica a una distribución exponencial equivalente a dos (valor igual a la mitad).

Función de distribución acumulativa complementaria (distribución de cola)

Función de distribución acumulativa complementaria (ccdf) o Distribución de la cola se define como ${displaystyle {overline {F}(mathbf {x})=1-mathbb {P} (mathbf {X} leq mathbf {x})}$. Cuando ${displaystyle mathbf {X} sim {mathcal {N}({boldsymbol {mu }},,{boldsymbol {Sigma }}}}}}$, entonces el ccdf puede ser escrito como una probabilidad el máximo de variables Gaussianas dependientes:

${displaystyle {fnMitbf {x}=mathbb {P} left(bigcup ¿Qué? ¿Por qué?$

Si bien no existe una fórmula cerrada simple para calcular el ccdf, el máximo de variables gaussianas dependientes puede estimarse con precisión mediante el método de Monte Carlo.

Propiedades

Probabilidad en diferentes dominios

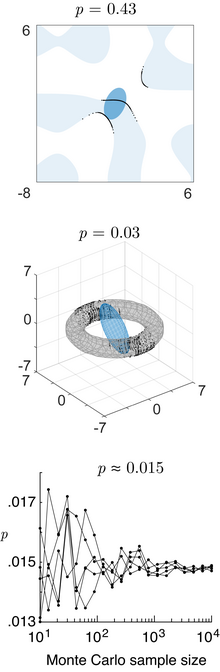
Top: la probabilidad de una normalidad bivariada en el dominio ${displaystyle xsin y-ycos x confianza1}$ (reglas azules). Medio: la probabilidad de una normalidad trivariada en un dominio toroidal. Tema: converger Monte-Carlo integral de la probabilidad de una normalidad 4-variada en el dominio poliedral normal 4d definido por ${displaystyle sum ##{i=1} {4}vert x_{i}vert.$. Todos estos son computados por el método numérico de rastreo de rayos.

El contenido de probabilidad de la normalidad multivariable en un dominio cuadrático definido por ${fnK}'Mathbf {fnK} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft} {fnK}}} {fnK}} {fnK}}} {fnK}}} {f}}} {f}}}}}}}} {f}}}}}}}}}} { {x}+{boldsymbol {q_{1} {fn} {fnK}} {fnK}}} {\fnK}}} {\fn}}}}} { {x}+q_{0} {0}}$ (donde) ${displaystyle mathbf {Q_{2}$ es una matriz, ${displaystyle {boldsymbol {q_{1}}}$ es un vector, y ${displaystyle q_{0}$ es un escalar), que es relevante para la clasificación Bayesian / teoría de la decisión usando el análisis discriminante gausiano, es dada por la distribución generalizada de chi-squared. El contenido de probabilidad dentro de cualquier dominio general definido por ${displaystyle f({boldsymbol {x}}}} {}}}}} {f}$ (donde) ${displaystyle f({boldsymbol {x})}$ es una función general) se puede calcular utilizando el método numérico de rastreo de rayos (código principal).

Momentos superiores

Los momentos de késimo orden de x están dados por

${displaystyle mu _{1,ldotsN}(mathbf {x}) {fnMicrosoft} } {=} mu _{1},ldotsr_{N}(mathbf {x}) {fnMicrosoft} - ¿Qué? {E} left[prod] ¿Qué?$

donde r₁ + r₂ + ⋯ + r_N = k.

Los momentos centrales de késimo orden son los siguientes

donde se toma la suma sobre todas las asignaciones del conjunto ${displaystyle left{1,ldots2lambdaright}}$ en λ (sin orden) pares. Eso es, para un kT (= 2λ = 6) momento central, uno resume los productos de λ = 3 covarianzas (el valor esperado) μ se considera 0 en interés de la parsimonia:

${displaystyle {begin{aligned}&operatorname {E} [X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}]\[8pt]={}&operatorname {E} [X_{1}X_{2}]operatorname {E} [X_{3}X_{4}]operatorname {E} [X_{5}X_{6}]+operatorname {E} [X_{1}X_{2}]operatorname {E} [X_{3}X_{5}]operatorname {E} [X_{4}X_{6}]+operatorname {E} [X_{1}X_{2}]operatorname {E} [X_{3}X_{6}]operatorname {E} [X_{4}X_{5}]\[4pt]&{}+operatorname {E} [X_{1}X_{3}]operatorname {E} [X_{2}X_{4}]operatorname {E} [X_{5}X_{6}]+operatorname {E} [X_{1}X_{3}]operatorname {E} [X_{2}X_{5}]operatorname {E} [X_{4}X_{6}]+operatorname {E} [X_{1}X_{3}]operatorname {E} [X_{2}X_{6}]operatorname {E} [X_{4}X_{5}]\[4pt]&{}+operatorname {E} [X_{1}X_{4}]operatorname {E} [X_{2}X_{3}]operatorname {E} [X_{5}X_{6}]+operatorname {E} [X_{1}X_{4}]operatorname {E} [X_{2}X_{5}]operatorname {E} [X_{3}X_{6}]+operatorname {E} [X_{1}X_{4}]operatorname {E} [X_{2}X_{6}]operatorname {E} [X_{3}X_{5}]\[4pt]&{}+operatorname {E} [X_{1}X_{5}]operatorname {E} [X_{2}X_{3}]operatorname {E} [X_{4}X_{6}]+operatorname {E} [X_{1}X_{5}]operatorname {E} [X_{2}X_{4}]operatorname {E} [X_{3}X_{6}]+operatorname {E} [X_{1}X_{5}]operatorname {E} [X_{2}X_{6}]operatorname {E} [X_{3}X_{4}]\[4pt]&{}+operatorname {E} [X_{1}X_{6}]operatorname {E} [X_{2}X_{3}]operatorname {E} [X_{4}X_{5}]+operatorname {E} [X_{1}X_{6}]operatorname {E} [X_{2}X_{4}]operatorname {E} [X_{3}X_{5}]+operatorname {E} [X_{1}X_{6}]operatorname {E} [X_{2}X_{5}]operatorname {E} [X_{3}X_{4}].end{aligned}}}$

Este rendimiento ${fnMicroc {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {ccfnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {ccccHFF}fnMicrosoft {fnMicrosoft {fnMicrosoft {cfnMicrosoft {\fnMicrosoft {fnMicrosoft {ccfnMicrosoft {\fnMicrosoft {fnMicrosoft {cc\\\\\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\c\\cfnMicrosoft {fnMi -1)! -1}(lambda -1)!$ términos en la suma (15 en el caso anterior), siendo cada uno el producto de λ (en este caso 3) covarianzas. Para los momentos de cuarto orden (cuatro variables) hay tres términos. Para los momentos de sexto orden hay 3 × 5 = 15 términos, y para los momentos de octavo orden hay 3 × 5 × 7 = 105 términos.

Las covarianzas se determinan luego reemplazando los términos de la lista ${displaystyle [1,ldots2lambda]$ por los términos correspondientes de la lista r₁ entonces r₂ dos, etc. Para ilustrar esto, examine el siguiente caso de cuarto orden del momento central:

${displaystyle {begin{aligned}operatorname {E} left[X_{i}}{4}right] implica=3sigma _{ii}^{2}[4pt]operatorname {E} left[X_{i}^{3}X_{j}right] {E} left[X_{i}{2}X_{j}{2}right=sigma ¿Qué? _{jj}+2sigma ################################################################################################################################################################################################################################################################ ¿Qué? _{jk}+2sigma _{ij}sigma ¿Por qué? {E} left [X_{i}X_{j}X_{k}X_{n}right] _{ij}sigma ¿Por qué? _{ik}sigma _{jn}+sigma ¿Qué? ¿Qué?$

Donde ${displaystyle sigma _{ij}$ es la covariancia de X_i y X_j. Con el método anterior se encuentra primero el caso general para un kmomento con k diferentes X variables, ${displaystyle Eleft[X_{i}X_{j}X_{k}X_{n}right]$, y luego uno simplifica esto en consecuencia. Por ejemplo, ${displaystyle operatorname [X_{i}{2}X_{k}X_{n}$, uno deja X_i = X_j y uno utiliza el hecho de que ${displaystyle sigma # {ii}=sigma ¿Qué?$.

Funciones de un vector normal

a: Densidad de probabilidad de una función ${displaystyle cos x^{2}$ de una sola variable normal ${displaystyle x}$ con ${displaystyle mu =-2}$ y ${displaystyle sigma =3}$. b: Densidad de probabilidad de una función ${displaystyle x^{y}$ de un vector normal ${displaystyle (x,y)}$, con mala ${displaystyle {boldsymbol {mu}=(1,2)}$, y covariancia ${displaystyle mathbf {Sigma } ={begin{bmatrix}.01 limit.016\.016 pp.04end{bmatrix}}}}$. c: Mapa de calor de la densidad de probabilidad conjunta de dos funciones de un vector normal ${displaystyle (x,y)}$, con mala ${displaystyle {boldsymbol {mu}=(-2,5)}$, y covariancia ${displaystyle mathbf {Sigma } ={begin{bmatrix}10 coinciden con 7\\\7]$. d: Densidad de probabilidad de una función ${displaystyle sum _{i=1}{4}vert x_{i}vert$ de 4 variables normales normales. Estos son computados por el método numérico de rastreo de rayos.

Una forma cuadrática de un vector normal ${displaystyle {boldsymbol {x}}$, ${fnK}'Mathbf {fnK} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft} {fnK}}} {fnK}} {fnK}}} {fnK}}} {f}}} {f}}}}}}}} {f}}}}}}}}}} { {x}+{boldsymbol {q_{1} {fn} {fnK}} {fnK}}} {\fnK}}} {\fn}}}}} { {x}+q_{0}$ (donde) ${displaystyle mathbf {Q_{2}$ es una matriz, ${displaystyle {boldsymbol {q_{1}}}$ es un vector, y ${displaystyle q_{0}$ es un cuero cabelludo), es una variable cisterna generalizada.

Si ${displaystyle f({boldsymbol {x})}$ es una función general de valor de escalar de un vector normal, su función de densidad de probabilidad, la función de distribución acumulativa y la función de distribución acumulativa inversa se pueden computar con el método numérico de rastreo de rayos (código principal).

Función de probabilidad

Si se conoce la matriz media y covariancia, la probabilidad de registro de un vector observado ${displaystyle {boldsymbol {x}}$ es simplemente el registro de la función de densidad de probabilidad:

${displaystyle ln L({boldsymbol {x})=-{frac {1}{2}}left[ln(Prince {boldsymbol {Sigma })+({boldsymbol {x}-{boldsymbol {mu}})'{boldsymbol {Sigma ################################################################################################################################################################################################################################################################ {x}-{boldsymbol {mu})+kln(2pi)right]}$,

La versión circular simétrica del caso complejo no central, donde ${displaystyle {boldsymbol {z}}$ es un vector de números complejos, sería

${displaystyle ln L({boldsymbol {z})=-ln(Sobrevivir{boldsym {bolSigma } sobrevivir,)-({boldsymbol {Z}-{boldsymbol {mu}})}{dagger }{boldsymbol {Sigma} {fnMicrosoft Sans Serif} {z}-{boldsymbol {mu}})-kln(pi)}$

i.e. con la transposición conyugal (indicada por ${displaystyle dagger }$) sustitución de la transposición normal (indicado por ${displaystyle}$). Esto es ligeramente diferente que en el caso real, porque la versión circular simétrica de la distribución normal compleja tiene una forma ligeramente diferente para la constante de normalización.

Se utiliza una notación similar para la regresión lineal múltiple.

Dado que el logaritmo de verosimilitud de un vector normal es una forma cuadrática del vector normal, se distribuye como una variable de chi-cuadrado generalizada.

Entropía diferencial

La entropía diferencial de la distribución normal multivariada es

${displaystyle {begin{aligned}hleft(fright) - No. _{-infty }{infty }cdots int _{-infty } {infty }f(mathbf {x})ln f(mathbf {x}),dmathbf {x}\\\fnMicroc {1}{2}}lnlnleft {left {Sigma }}justo de la vidaderecha)={frac {1}{2}ln left(left(2pi eright)}left sometida{boldsymbol {Sigma }}derechoderecha)={frac {k}{2}ln left(2pi eright)+{frac {1}{2}ln left(left perpetua{boldsymbol) {Sigma }right sobre la vidaright)={frac {k}{2}}+{frac {k}{2}}ln left(2pi right)+{frac {1}{2}}ln left(left perpetua{boldsymbol {Sigma }justo de la vidaderecha)\fnMicrosoft Sans Serif}}$

donde las barras indican el determinante de la matriz y k es la dimensionalidad del espacio vectorial.

Divergencia Kullback-Leibler

La divergencia Kullback-Leibler desde ${displaystyle {máthcal {fn}_{1}({boldsymbol {mu} }_{1},{boldsymbol {Sigma - Sí.$ a ${fnK} {fnh} {fnh00} {fnfnK} {fnh} {\fn}} {fn}} {\fnfnfnfnfnfnfnfnfnfnfnfnfnK}fnfnfnK}}}fnh}\fnK\fn\\fn\fnKfnKfnfnKfnh00fnK\fnK}\\fnK}}\\fnK\\fnK\fnKfnK}fnK}\fnKfnK\fnKfnK}\\fnKfnKfnKfnK}\\\\fnKfnK}}}}}} }_{0},{boldsymbol {Sigma }$, para matrices no singulares₁ y la₀, es:

${displaystyle D_{text{KL} {N}_{0}parallel {fn}_{1})={1over 2}left{fnh} left({boldsymbol {Sigma }_{1} {-1}{boldsymbol {Sigma }_{0}right)+left({boldsymbol # }_{1}-{boldsymbol # Está bien. {T}{boldsymbol {Sigma }_{1} {-1} {boldsymbol {mu} }_{1}-{boldsymbol # }_{0})-k+ln {fnMicrosoft {fnh} {Sigma }_{1} sobre la vida {Sigma - Hola.$

Donde ${displaystyle k}$ es la dimensión del espacio vectorial.

El logaritmo debe tomarse en base e ya que los dos términos que siguen al logaritmo son en sí mismos logaritmos en base e de expresiones que son factores de la función de densidad o no surgen naturalmente. Por lo tanto, la ecuación da un resultado medido en nats. Dividir toda la expresión anterior por log_e 2 produce la divergencia en bits.

Cuando ${displaystyle {boldsymbol {mu} }_{1}={boldsymbol {mu }$,

${displaystyle D_{text{KL} {N}_{0}parallel {fn}_{1})={1over 2}left{fnh} left({boldsymbol {Sigma }_{1} {-1}{boldsymbol {Sigma }_{0}right)-k+ln {fnMicrosoft {fnh} {Sigma }_{1} sobre la vida {Sigma - Hola.$

Información mutua

La información mutua de una distribución es un caso especial de la divergencia Kullback-Leibler en el que ${displaystyle P}$ es la distribución multivariada completa y ${displaystyle Q}$ es el producto de las distribuciones marginales de 1 dimensión. En la notación de la sección de divergencias Kullback-Leibler de este artículo, ${displaystyle {boldsymbol {Sigma }_{1}$ es una matriz diagonal con las entradas diagonales de ${displaystyle {boldsymbol {Sigma }$, y ${displaystyle {boldsymbol {mu} }_{1}={boldsymbol {mu }$. La fórmula resultante para la información mutua es:

${displaystyle I({boldsymbol {X}})=-{1over 2}ln Ных{boldsymbol {rho - Hola.$

Donde ${displaystyle {boldsymbol} }$ es la matriz de correlación construida a partir de ${displaystyle {boldsymbol {Sigma }$.

En el caso bivariado la expresión para la información mutua es:

${displaystyle I(x;y)=-{1over 2}ln(1-rho ^{2}). }$

Normalidad articular

Normalmente distribuidos e independientes

Si ${displaystyle X}$ y ${displaystyle Sí.$ son normalmente distribuidos e independientes, esto implica que son "juntamente distribuidos", es decir, el par ${displaystyle (X,Y)}$ debe tener una distribución normal multivariada. Sin embargo, un par de variables distribuidas conjuntamente normalmente no necesitan ser independientes (sólo sería así si no estuvieran relacionadas, ${displaystyle rho =0}$).

Dos variables aleatorias normalmente distribuidas no necesitan ser juntas normales bivariadas

El hecho de que dos variables al azar ${displaystyle X}$ y ${displaystyle Sí.$ ambos tienen una distribución normal no implica que el par ${displaystyle (X,Y)}$ tiene una distribución normal conjunta. Un ejemplo simple es uno en el que X tiene una distribución normal con el valor esperado 0 y la varianza 1, y ${displaystyle Y=X}$ si ${displaystyle Silencioso$ y ${displaystyle Y=-X}$ si ${displaystyle Silencioso$, donde ${displaystyle c]0}$. Hay contraexamples similares para más de dos variables aleatorias. En general, se suma a un modelo de mezcla.

Correlaciones e independencia

En general, las variables aleatorias pueden no estar correlacionadas pero ser estadísticamente dependientes. Pero si un vector aleatorio tiene una distribución normal multivariada, entonces dos o más de sus componentes que no están correlacionados son independientes. Esto implica que dos o más de sus componentes que son independientes por pares son independientes. Pero, como se señaló anteriormente, no es cierto que dos variables aleatorias que están (por separado, marginalmente) normalmente distribuidas y no correlacionadas son independientes.

Distribuciones condicionales

Si N-dimensional x se divide de la siguiente manera

${displaystyle mathbf {x} ={begin{bmatrix}mathbf {x} _{1}\mathbf {x} _{2}end{bmatrix}{text{ with sizes}{begin{bmatrix}qtimes 1(N-q)times 1end{btrix}trimtrix} {btrix}$

y, en consecuencia, μ y Σ se dividen de la siguiente manera

${displaystyle {boldsymbol {mu} {begin{bmatrix}{boldsymbol # }_{1}\\\\\\m2}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\cH\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}} {begin{bmatrix}qtimes 1(N-q)times 1end{bmatrix}}}}$

${displaystyle {boldsymbol {Sigma {begin{bmatrix}{boldsymbol {Sigma }_{11} {boldsymbol {Sigma }_{12}\\\\\\\\\\\\\\\\\\cH003\\\\\\\\\\\\\\\\\\\\\\cH3\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\cH {Sigma }_{21} {boldsymbol {Sigma {}} {22}end{bmatrix}}{text{ with sizes }{begin{bmatrix}qtimes q limitqtimes (N-q)(N-q)times q limites (N-q)times (N-q)end{bmatrix}}}}}}}}}}$

entonces la distribución de x₁ condicionada a x₂ = a es normal multivariado (x₁ | x₂ = a ) ~ N(μ, Σ) donde

${displaystyle {bar {boldsymbol {mfnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\fnMicrosoft {\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ }={boldsymbol {mu }_{1}+{boldsymbol {Sigma }_{12}{boldsymbol {Sigma }_{22} {-1}left(mathbf {a} - ¿Qué? - Sí.$

y matriz de covarianza

${displaystyle {overline {boldsymbol {Sigma }={boldsymbol {Sigma }_{11}-{boldsymbol {Sigma }_{12}{boldsymbol {Sigma }_{22} {-1}{boldsymbol {Sigma - Sí.$

Aquí. ${displaystyle {boldsymbol {Sigma - Sí.$ es el inverso generalizado de ${displaystyle {boldsymbol {Sigma }_{22}$. La matriz ${displaystyle {overline {boldsymbol {Sigma }$ es el complemento de Schur .₂₂ dentro .. Es decir, la ecuación anterior es equivalente a invertir la matriz de covariancia general, bajando las filas y columnas correspondientes a las variables que están condicionadas, e invirtiendo de nuevo para conseguir la matriz de covariancia condicional.

Note que sabiendo que x₂ = a altera la varianza, aunque la nueva varianza no depende del valor específico de a; quizás más sorprendentemente, la media es cambiada por ${displaystyle {boldsymbol {Sigma }_{12}{boldsymbol {Sigma }_{22} {-1}left(mathbf {a} - ¿Qué? - Sí.$; comparar esto con la situación de no conocer el valor a, en cuyo caso x₁ tendría distribución ${displaystyle {Mathcal {N}_{q}left({boldsymbol # }_{1},{boldsymbol Sí.$.

Un hecho interesante derivado para probar este resultado, es que los vectores aleatorios ${displaystyle mathbf {x} ¿Qué?$ y ${displaystyle mathbf {y} ¿Qué? _{1}-{boldsymbol {Sigma }_{12}{boldsymbol {Sigma - ¿Qué? ¿Qué?$ son independientes.

La matriz Σ₁₂Σ₂₂⁻¹ se conoce como la matriz de coeficientes de regresión.

Caso bivariado

En el caso bivariado x se divide en ${displaystyle X_{1}$ y ${displaystyle X_{2}$, la distribución condicional de ${displaystyle X_{1}$ dado ${displaystyle X_{2}$ es

${displaystyle X_{1}mid X_{2}=a\\sim {\m1}mátcal {N}left(mu _{1}+{frac {sigma _{1}{sigma _{2}}}rho (a-mu _{2}),,(1-rho ^{2})sigma _{1}{2}right). }$

Donde ${displaystyle rho }$ es el coeficiente de correlación entre ${displaystyle X_{1}$ y ${displaystyle X_{2}$.

Expectativa condicional bivariada

En el caso general

${fnK}mfnK}m}m}pm}m}sim {cH0}m}sim {m}sim {m}m}m}m}m}b9pbegin{begin{pmatrix}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}m}b}m}m}sim}m}m}m}b9}m}b}m}m}m}b}m}m}m}m}m}m}b9}b}b9}b}b}cb}b}b}b9} ¿Por qué? ########### {begin{pmatrix}sigma ################################################################################################################################################################################################################################################################ _{2}\\\rho sigma _{1}sigma - ¿Qué? ¿Qué?$

La expectativa condicional de X₁ dada X₂ es:

${displaystyle operatorname {E} (X_{1}mid X_{2}=x_{2}=mu ¿Por qué? {sigma ¿Qué?$

Prueba: el resultado se obtiene tomando la expectativa de la distribución condicional ${displaystyle X_{1}mid X_{2}$ arriba.

En el caso centrado con varianzas unitarias

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMitcal {fn}m}}sim {m}sim {begin{begin{pmatrix}0$