Distancia de hamming

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Número de bits que difieren entre dos cuerdas

Cubo binario de 3 bits para encontrar distancia Hamming

Dos distancias de ejemplo: 100→011 tiene distancia 3; 010→111 tiene distancia 2

La distancia mínima entre los dos vértices es la distancia Hamming entre las dos cadenas binarias.

En la teoría de la información, la distancia de Hamming entre dos cadenas de igual longitud es el número de posiciones en las que los símbolos correspondientes son diferentes. En otras palabras, mide el número mínimo de sustituciones necesarias para cambiar una cadena por otra, o el número mínimo de errores que podrían haber transformado una cadena en otra. En un contexto más general, la distancia de Hamming es una de varias métricas de cadena para medir la distancia de edición entre dos secuencias. Lleva el nombre del matemático estadounidense Richard Hamming.

Una aplicación importante es en la teoría de la codificación, más específicamente en los códigos de bloque, en los que las cadenas de igual longitud son vectores sobre un campo finito.

Definición

La distancia de Hamming entre dos cadenas de símbolos de igual longitud es el número de posiciones en las que los símbolos correspondientes son diferentes.

Ejemplos

Los símbolos pueden ser letras, bits o dígitos decimales, entre otras posibilidades. Por ejemplo, la distancia de Hamming entre:

"karoldentro"y"kathrdentro"Es 3.
"karoldentro"y"kerstdentro"Es 3.
"kFRANCÉSdentro"y"kErstdentro"Es 4.
0000 y 1111 4.
2173896 y 2233796 3.

Propiedades

Para una longitud fija n, la distancia de Hamming es una métrica sobre el conjunto de las palabras de longitud n (también conocido como espacio de Hamming), ya que cumple las condiciones de no negatividad, simetría, la distancia de Hamming de dos palabras es 0 si y solo si las dos palabras son idénticas, y también satisface la desigualdad del triángulo: De hecho, si fijamos tres palabras a, b y c, entonces siempre que haya una diferencia entre la iésima letra de a y la iésima letra de c, entonces debe haber una diferencia entre la iésima letra de a y iésima letra de b, o entre la iésima letra de b y la iésima letra de c. Por lo tanto, la distancia de Hamming entre a y c no es mayor que la suma de las distancias de Hamming entre a y b y entre b y c. La distancia de Hamming entre dos palabras a y b también se puede ver como el peso de Hamming de a − b para una elección apropiada del operador −, al igual que la diferencia entre dos números enteros puede verse como una distancia desde cero en la recta numérica.

Para cadenas binarias a y b la distancia Hamming es igual al número de los (conteo de la población) en a XOR b. El espacio métrico de longitud...n cadenas binarias, con la distancia Hamming, se conoce como el Cubo de afeitar; es equivalente como un espacio métrico al conjunto de distancias entre vértices en un gráfico hipercubo. También se puede ver una cadena binaria de longitud n como vector en $mathbb {R} ^{n}$ tratando cada símbolo en la cuerda como una verdadera coordinación; con esta incrustación, las cuerdas forman los vértices de un n- hipercubo dimensional, y la distancia Hamming de las cuerdas es equivalente a la distancia de Manhattan entre los vértices.

Detección y corrección de errores

La distancia mínima de Hamming se utiliza para definir algunas nociones esenciales en la teoría de la codificación, como los códigos de detección y corrección de errores. En particular, se dice que un código C tiene un error k al detectar si, y solo si, la distancia mínima de Hamming entre dos de sus palabras clave es al menos k +1.

Por ejemplo, considere el código que consta de dos palabras clave "000" y "111". La distancia de hamming entre estas dos palabras es 3, y por lo tanto es k=2 detección de errores. Esto significa que si se invierte un bit o se invierten dos bits, se puede detectar el error. Si se invierten tres bits, entonces "000" se convierte en "111" y el error no puede ser detectado.

Se dice que un código C es k-corrección de errores si, para cada palabra w en el espacio de Hamming subyacente H , existe como máximo una palabra clave c (de C) tal que la distancia de Hamming entre w y c es como mucho k. En otras palabras, un código tiene errores de corrección k si, y solo si, la distancia mínima de Hamming entre dos de sus palabras clave es al menos 2k+1. Esto se entiende más fácilmente geométricamente como cualquier bola cerrada de radio k centrada en distintas palabras de código separadas. Estas bolas también se denominan esferas de Hamming en este contexto.

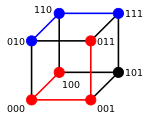
Por ejemplo, considere el mismo código de 3 bits que consta de dos palabras de código "000" y "111". El espacio de Hamming consta de 8 palabras 000, 001, 010, 011, 100, 101, 110 y 111. La palabra clave "000" y las palabras de error de bit único "001", "010", "100" son todos menores o iguales a la distancia de Hamming de 1 a "000". Del mismo modo, la palabra clave "111" y sus palabras de error de bit único "110","101" y "011" están todos dentro de una distancia de 1 Hamming del "111" original. En este código, un error de un solo bit siempre está dentro de la distancia de 1 Hamming de los códigos originales, y el código puede ser corrección de 1 error, es decir, k=1. La distancia mínima de Hamming entre "000" y "111" es 3, que satisface 2k+1 = 3.

Por lo tanto, un código con una distancia de Hamming mínima d entre sus palabras de código puede detectar como máximo errores d-1 y puede corregir ⌊(d- 1)/2⌋ errores. El último número también se denomina radio de empaquetamiento o capacidad de corrección de errores del código.

Historia y aplicaciones

La distancia de Hamming lleva el nombre de Richard Hamming, quien introdujo el concepto en su artículo fundamental sobre los códigos de Hamming, Códigos de detección y corrección de errores, en 1950. El análisis de peso de Hamming de bits se utiliza en varios disciplinas que incluyen la teoría de la información, la teoría de la codificación y la criptografía.

Se utiliza en telecomunicaciones para contar el número de bits volteados en una palabra binaria de longitud fija como una estimación de error, y por lo tanto se llama a veces el distancia de señal. Para q- hilos diarios sobre un alfabeto de tamaño q≥ 2 la distancia Hamming se aplica en el caso del canal simétrico q-ary, mientras que la distancia Lee se utiliza para el keying por fase o canales más generalmente susceptibles a errores de sincronización porque la distancia Lee explica errores de ±1. Si $q=2$ o ${displaystyle q=3}$ ambas distancias coinciden porque cualquier par de elementos de ${textstyle mathbb {Z} /2mathbb {Z} }$ o ${textstyle mathbb {Z} /3mathbb {Z} }$ diferir por 1, pero las distancias son diferentes para mayor $q$ .

La distancia de Hamming también se usa en sistemática como una medida de la distancia genética.

Sin embargo, para comparar cadenas de diferentes longitudes, o cadenas en las que no solo se esperan sustituciones sino también inserciones o eliminaciones, es más apropiada una métrica más sofisticada como la distancia de Levenshtein.

Ejemplo de algoritmo

La siguiente función, escrita en Python 3, devuelve la distancia de Hamming entre dos cadenas:

def Hamming_distance()string1, string2): si ()Len()string1) ! Len()string2) aumento Excepción()Las cuerdas deben ser de igual longitud. ') dist_counter = 0 para n dentro rango()Len()string1) si string1[n] ! string2[n]: dist_counter += 1 retorno dist_counter

O, en una expresión más corta:

suma()xi ! Yi para xi, Yi dentro Cierre()x, Sí.)

La función hamming_distance(), implementada en Python 3, calcula la distancia de Hamming entre dos cadenas (u otros objetos iterables) de igual longitud mediante la creación de una secuencia de valores booleanos que indican discrepancias y coincidencias entre cadenas correspondientes. posiciones en las dos entradas, luego sumando la secuencia con valores Verdadero y Falso, interpretados como uno y cero, respectivamente.

def Hamming_distance()s1, s2) - int: ""Retorna la distancia Hamming entre secuencias de longitud igual."" si Len()s1) ! Len()s2): aumento ValueError()"Definido para secuencias de longitud desigual.") retorno suma()el1 ! el2 para el1, el2 dentro Cierre()s1, s2)

donde la función zip() fusiona dos colecciones de igual longitud en pares.

La siguiente función C calculará la distancia de Hamming de dos enteros (considerados como valores binarios, es decir, como secuencias de bits). El tiempo de ejecución de este procedimiento es proporcional a la distancia de Hamming más que al número de bits en las entradas. Calcula el o exclusivo bit a bit de las dos entradas, y luego encuentra el peso de Hamming del resultado (el número de bits distintos de cero) utilizando un algoritmo de Wegner (1960) que encuentra y borra repetidamente el bit distinto de cero de orden más bajo. Algunos compiladores admiten la función __builtin_popcount que puede calcular esto utilizando hardware de procesador especializado donde esté disponible.

int Hamming_distance()no firmado x, no firmado Sí.){} int No. = 0; // Los operadores ^ se fijan a 1 sólo los bits que son diferentes para ()no firmado val = x ^ Sí.; val ■ 0; ++No.) {} // Entonces contamos el bit set a 1 usando la forma Peter Wegner val = val " ()val - 1); // Se establece a cero el orden más bajo de Val 1 } // Devuelve el número de bits diferentes retorno No.;}

Una alternativa más rápida es usar la instrucción de ensamblado de conteo de población (popcount). Ciertos compiladores como GCC y Clang lo hacen disponible a través de una función intrínseca:

// Distancia de regulación para enteros de 32 bitsint hamming_distance32()no firmado int x, no firmado int Sí.){} retorno __ builtin_popcount()x ^ Sí.);}// Distancia de regulación para enteros de 64 bitsint hamming_distance64()no firmado largo largo x, no firmado largo largo Sí.){} retorno __ builtin_popcountll()x ^ Sí.);}

Contenido relacionado

Más resultados...