Dispersión (óptica)
En óptica y en la propagación de ondas en general, la dispersión es el fenómeno en el que la velocidad de fase de una onda depende de su frecuencia; a veces, el término dispersión cromática se utiliza para la especificidad de la óptica en particular. Un medio que tenga esta propiedad común puede denominarse medio dispersivo (plural medio dispersivo).
Aunque el término se utiliza en el campo de la óptica para describir la luz y otras ondas electromagnéticas, la dispersión en el mismo sentido puede aplicarse a cualquier tipo de movimiento ondulatorio, como la dispersión acústica en el caso del sonido y las ondas sísmicas, y en la gravedad. olas (olas del mar). Dentro de la óptica, la dispersión es una propiedad de las señales de telecomunicaciones a lo largo de las líneas de transmisión (como las microondas en el cable coaxial) o los pulsos de luz en la fibra óptica.
En óptica, una consecuencia importante y familiar de la dispersión es el cambio en el ángulo de refracción de diferentes colores de luz, como se ve en el espectro producido por un prisma dispersivo y en la aberración cromática de las lentes. El diseño de lentes acromáticas compuestas, en las que la aberración cromática se cancela en gran medida, utiliza una cuantificación de la dispersión de un vidrio dada por su número de Abbe V, donde los números de Abbe más bajos corresponden a una mayor dispersión en el espectro visible. En algunas aplicaciones, como las telecomunicaciones, la fase absoluta de una onda a menudo no es importante, sino solo la propagación de paquetes de ondas o "pulsos"; en ese caso, uno está interesado solo en las variaciones de la velocidad de grupo con la frecuencia, la llamada dispersión de velocidad de grupo.
Todos los medios de transmisión comunes también varían en atenuación (normalizada a la longitud de transmisión) en función de la frecuencia, lo que genera distorsión de atenuación; esto no es dispersión, aunque a veces los reflejos en límites de impedancia poco espaciados (por ejemplo, segmentos engarzados en un cable) pueden producir una distorsión de la señal que agrava aún más el tiempo de tránsito inconsistente observado en todo el ancho de banda de la señal.
Ejemplos
El ejemplo más conocido de dispersión es probablemente un arcoíris, en el que la dispersión provoca la separación espacial de una luz blanca en componentes de diferentes longitudes de onda (diferentes colores). Sin embargo, la dispersión también tiene un efecto en muchas otras circunstancias: por ejemplo, la dispersión de velocidad de grupo hace que los pulsos se propaguen en las fibras ópticas, degradando las señales en largas distancias; además, una cancelación entre la dispersión de velocidad de grupo y los efectos no lineales conduce a ondas de solitón.
Dispersión de material y guía de ondas
La mayoría de las veces, la dispersión cromática se refiere a la dispersión del material a granel, es decir, el cambio en el índice de refracción con la frecuencia óptica. Sin embargo, en una guía de ondas también existe el fenómeno de la dispersión de la guía de ondas, en cuyo caso la velocidad de fase de una onda en una estructura depende de su frecuencia simplemente debido a la geometría de la estructura. Más generalmente, "guía de ondas" la dispersión puede ocurrir para ondas que se propagan a través de cualquier estructura no homogénea (por ejemplo, un cristal fotónico), ya sea que las ondas estén o no confinadas a alguna región. En una guía de onda, generalmente estarán presentes ambos tipos de dispersión, aunque no son estrictamente aditivos. Por ejemplo, en la fibra óptica, la dispersión del material y la guía de ondas pueden cancelarse entre sí de manera efectiva para producir una longitud de onda de dispersión cero, importante para una comunicación rápida de fibra óptica.
Dispersión de materiales en óptica
La dispersión del material puede ser un efecto deseable o indeseable en las aplicaciones ópticas. La dispersión de la luz por prismas de vidrio se utiliza para construir espectrómetros y espectrorradiómetros. Sin embargo, en las lentes, la dispersión provoca aberración cromática, un efecto no deseado que puede degradar las imágenes en microscopios, telescopios y objetivos fotográficos.
La velocidad de fase v de una onda en un medio uniforme dado viene dada por
- v=cn,{displaystyle v={frac {c} {n}},}
donde c es la velocidad de la luz en el vacío, y n es el índice de refracción del medio.
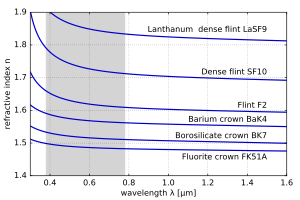
En general, el índice de refracción es una función de la frecuencia f de la luz, por lo que n = n(f ), o alternativamente, con respecto a la longitud de onda de la onda n = n(λ). La dependencia de la longitud de onda del índice de refracción de un material generalmente se cuantifica por su número de Abbe o sus coeficientes en una fórmula empírica como las ecuaciones de Cauchy o Sellmeier.
Debido a las relaciones de Kramers-Kronig, la dependencia de la longitud de onda de la parte real del índice de refracción está relacionada con la absorción del material, descrita por la parte imaginaria del índice de refracción (también llamado coeficiente de extinción). En particular, para materiales no magnéticos (μ = μ0), la susceptibilidad χ que aparece en las relaciones de Kramers-Kronig es la susceptibilidad eléctrica χe = n2 − 1.
La consecuencia más común de la dispersión en la óptica es la separación de la luz blanca en un espectro de color mediante un prisma. De la ley de Snell se puede ver que el ángulo de refracción de la luz en un prisma depende del índice de refracción del material del prisma. Dado que el índice de refracción varía con la longitud de onda, se deduce que el ángulo por el que se refracta la luz también variará con la longitud de onda, provocando una separación angular de los colores conocida como dispersión angular.
Para la luz visible, los índices de refracción n de la mayoría de los materiales transparentes (p. ej., aire, vidrios) disminuyen al aumentar la longitud de onda λ:
- <math alttext="{displaystyle 1<n(lambda _{text{red}})<n(lambda _{text{yellow}})1.n()λ λ rojo).n()λ λ amarillo).n()λ λ azul),{displaystyle 1 maden(lambda _{text{red}})se hizo(lambda _{text{yellow}}) se hizo(lambda _{text{blue}})}<img alt="{displaystyle 1<n(lambda _{text{red}})<n(lambda _{text{yellow}})
o generalmente,
- <math alttext="{displaystyle {frac {dn}{dlambda }}dndλ λ .0.{displaystyle {frac {}{dlambda - No.<img alt="{displaystyle {frac {dn}{dlambda }}
En este caso, se dice que el medio tiene dispersión normal. Mientras que si el índice aumenta con el aumento de la longitud de onda (que suele ser el caso en el ultravioleta), se dice que el medio tiene dispersión anómala.
En la interfaz de dicho material con el aire o el vacío (índice de ~1), la ley de Snell predice que la luz que incide en un ángulo θ con respecto a la normal se refractará a una ángulo arcsin(sin θ/n). Por lo tanto, la luz azul, con un índice de refracción más alto, se desviará con más fuerza que la luz roja, lo que dará como resultado el conocido patrón de arco iris.
Dispersión de velocidad de grupo
Más allá de simplemente describir un cambio en la velocidad de fase sobre la longitud de onda, una consecuencia más grave de la dispersión en muchas aplicaciones se denomina dispersión de velocidad de grupo (GVD). Mientras que la velocidad de fase v se define como v = c/n, esto describe solo un componente de frecuencia. Cuando se combinan diferentes componentes de frecuencia, como cuando se considera una señal o un pulso, uno suele estar más interesado en la velocidad del grupo, que describe la velocidad a la que se propaga un pulso o información superpuesta a una onda (modulación). En la animación adjunta, se puede ver que la propia onda (naranja-marrón) viaja a una velocidad de fase mucho más rápida que la velocidad de la envolvente (negra), que corresponde a la velocidad del grupo. Este pulso podría ser una señal de comunicaciones, por ejemplo, y su información solo viaja a la velocidad de grupo, aunque consiste en frentes de onda que avanzan a una velocidad más rápida (la velocidad de fase).
Es posible calcular la velocidad del grupo a partir de la curva del índice de refracción n(ω) o más directamente a partir del número de onda k = ωn/c, donde ω es la frecuencia en radianes ω = 2πf. Mientras que una expresión para la velocidad de fase es vp = ω/k, la velocidad de grupo se puede expresar usando la derivada: vg = dω/dk. O en términos de la velocidad de fase vp,
- vg=vp1− − ⋅ ⋅ vpdvpd⋅ ⋅ .{displaystyle ¿Qué? {V_{text{p}}{1-{dfrac {omega {fnK} {fnMicroc}} {fnMicroc}} {fnMicroc} {dv_{text{p} {domega - Sí.
Cuando hay dispersión, no solo la velocidad de grupo no es igual a la velocidad de fase, sino que generalmente varía con la longitud de onda. Esto se conoce como dispersión de velocidad de grupo y hace que un pulso de luz corto se amplíe, ya que los componentes de diferentes frecuencias dentro del pulso viajan a diferentes velocidades. La dispersión de la velocidad del grupo se cuantifica como la derivada del recíproco de la velocidad del grupo con respecto a la frecuencia angular, lo que da como resultado la dispersión de la velocidad del grupo = d2k/dω2.
Si un pulso de luz se propaga a través de un material con dispersión de velocidad de grupo positiva, entonces los componentes de longitud de onda más corta viajan más lentamente que los componentes de longitud de onda más larga. Por lo tanto, el pulso se convierte en chirrido positivo, o chirrido ascendente, aumentando en frecuencia con el tiempo. Por otro lado, si un pulso viaja a través de un material con dispersión de velocidad de grupo negativa, los componentes de longitud de onda más corta viajan más rápido que los más largos, y el pulso se convierte en chirrido negativo, o descendente. chirrido, disminuyendo en frecuencia con el tiempo.
Un ejemplo cotidiano de una señal con un chirrido negativo en el dominio acústico es el de un tren que se aproxima y golpea deformaciones en una vía soldada. El sonido que provoca el propio tren es impulsivo y viaja mucho más rápido en las vías metálicas que en el aire, por lo que el tren se puede oír mucho antes de que llegue. Sin embargo, desde lejos no se escucha que provoque impulsos, sino que conduce a un distintivo chirrido descendente, en medio de la reverberación causada por la complejidad de los modos vibratorios de la pista. La dispersión de la velocidad del grupo se puede escuchar porque el volumen de los sonidos permanece audible durante un tiempo sorprendentemente largo, hasta varios segundos.
El parámetro de dispersión de velocidad de grupo
- D=1cdndλ λ {displaystyle D={frac {1}{c},{frac} {dn}{dlambda }
se utiliza a menudo para cuantificar GVD, que es proporcional a D a través de un factor negativo:
- D=− − 2π π cλ λ 2d2kd⋅ ⋅ 2.{displaystyle D=-{frac {2pi c}{lambda ^{2}},{frac {d^{2}k}{domega }}}}}}
Según algunos autores, se dice que un medio tiene dispersión normal/dispersión anómala para una cierta longitud de onda de vacío λ0 si la segunda derivada del índice de refracción calculado en λ0 es positiva/negativa o, de forma equivalente, si D (λ0) es negativo/positivo. Esta definición se refiere a la dispersión de velocidad de grupo y no debe confundirse con la dada en la sección anterior. Las dos definiciones no coinciden en general, por lo que el lector debe comprender el contexto.
Control de dispersión
El resultado de la GVD, ya sea negativo o positivo, es, en última instancia, la propagación temporal del pulso. Esto hace que la gestión de la dispersión sea extremadamente importante en los sistemas de comunicaciones ópticas basados en fibra óptica, ya que si la dispersión es demasiado alta, un grupo de pulsos que representan un flujo de bits se dispersará en el tiempo y se fusionará, haciendo que el flujo de bits sea ininteligible. Esto limita la longitud de la fibra por la que se puede enviar una señal sin regeneración. Una posible respuesta a este problema es enviar señales por la fibra óptica a una longitud de onda en la que la GVD sea cero (p. ej., alrededor de 1,3 a 1,5 μm en fibras de sílice), de modo que los pulsos en esta longitud de onda sufran una dispersión mínima debido a la dispersión. En la práctica, sin embargo, este enfoque causa más problemas de los que resuelve porque cero GVD amplifica inaceptablemente otros efectos no lineales (como la mezcla de cuatro ondas). Otra posible opción es utilizar pulsos de solitones en régimen de dispersión negativa, una forma de pulso óptico que utiliza un efecto óptico no lineal para automantener su forma. Sin embargo, los solitones tienen el problema práctico de que requieren que se mantenga un cierto nivel de potencia en el pulso para que el efecto no lineal sea de la fuerza correcta. En su lugar, la solución que se usa actualmente en la práctica es realizar una compensación de la dispersión, típicamente haciendo coincidir la fibra con otra fibra de dispersión de signo opuesto para que los efectos de la dispersión se cancelen; dicha compensación está limitada en última instancia por efectos no lineales como la modulación de fase propia, que interactúa con la dispersión para que sea muy difícil de deshacer.
El control de la dispersión también es importante en los láseres que producen pulsos cortos. La dispersión global del resonador óptico es un factor importante para determinar la duración de los pulsos emitidos por el láser. Se puede disponer un par de prismas para producir una dispersión negativa neta, que se puede utilizar para equilibrar la dispersión generalmente positiva del medio láser. Las rejillas de difracción también se pueden usar para producir efectos dispersivos; estos se utilizan a menudo en sistemas amplificadores láser de alta potencia. Recientemente, se ha desarrollado una alternativa a los prismas y las rejillas: los espejos con chirrido. Estos espejos dieléctricos están revestidos de modo que diferentes longitudes de onda tengan diferentes longitudes de penetración y, por lo tanto, diferentes retardos de grupo. Las capas de recubrimiento se pueden adaptar para lograr una dispersión negativa neta.
En guías de ondas
Las guías de ondas son altamente dispersivas debido a su geometría (y no solo a la composición de su material). Las fibras ópticas son una especie de guía de ondas para frecuencias ópticas (luz) ampliamente utilizadas en los sistemas de telecomunicaciones modernos. La velocidad a la que se pueden transportar los datos en una sola fibra está limitada por el ensanchamiento del pulso debido a la dispersión cromática, entre otros fenómenos.
En general, para un modo de guía de onda con una frecuencia angular ω(β) a una constante de propagación β (de modo que los campos electromagnéticos en la dirección de propagación z oscila proporcional a ei(βz−ωt)), el parámetro de dispersión de velocidad de grupo D se define como
- D=− − 2π π cλ λ 2d2β β d⋅ ⋅ 2=2π π cvg2λ λ 2dvgd⋅ ⋅ ,{displaystyle D=-{frac {2pi {fnK} {fnK}} {fnMicroc {2}beta }{domega ^{2}={frac {2pi} {fnK} {fnK}} {fnK}} {f}} {fnK}}}} {fn}}}}
donde λ = 2πc/ ω es la longitud de onda del vacío, y vg = dω/dβ es la velocidad del grupo. Esta fórmula generaliza la de la sección anterior para medios homogéneos e incluye tanto la dispersión de la guía de ondas como la dispersión del material. La razón para definir la dispersión de esta manera es que |D| es el pulso temporal (asintótico) que se propaga Δt por unidad de ancho de banda Δλ por unidad de distancia recorrida, normalmente expresado en ps/(nm⋅km) para fibras ópticas.
En el caso de las fibras ópticas multimodo, la llamada dispersión modal también provocará un ensanchamiento del pulso. Incluso en fibras monomodo, el ensanchamiento del pulso puede ocurrir como resultado de la dispersión del modo de polarización (ya que todavía hay dos modos de polarización). Estos no son ejemplos de dispersión cromática, ya que no dependen de la longitud de onda o del ancho de banda de los pulsos propagados.
Dispersión de orden superior en anchos de banda amplios
Cuando un amplio rango de frecuencias (un amplio ancho de banda) está presente en un solo paquete de ondas, como en un pulso ultracorto o un pulso chirrido u otras formas de transmisión de espectro ensanchado, puede que no sea exacto aproximar la dispersión por un constante en todo el ancho de banda, y se requieren cálculos más complejos para computar efectos tales como la propagación del pulso.
En particular, el parámetro de dispersión D definido anteriormente se obtiene a partir de una sola derivada de la velocidad del grupo. Las derivadas superiores se conocen como dispersión de orden superior. Estos términos son simplemente una expansión en serie de Taylor de la relación de dispersión β(ω) del medio o guía de ondas alrededor de alguna frecuencia particular. Sus efectos se pueden calcular a través de la evaluación numérica de las transformadas de Fourier de la forma de onda, a través de la integración de aproximaciones de envolvente de variación lenta de orden superior, mediante un método de paso dividido (que puede usar la relación de dispersión exacta en lugar de una serie de Taylor), o por directa simulación de las ecuaciones completas de Maxwell en lugar de una ecuación envolvente aproximada.
Formulación generalizada de los altos órdenes de dispersión – óptica Lah-Laguerre
La descripción de la dispersión cromática de forma perturbativa a través de coeficientes de Taylor es ventajosa para problemas de optimización en los que es necesario equilibrar la dispersión de varios sistemas diferentes. Por ejemplo, en los amplificadores láser de pulso chirp, los pulsos se estiran primero en el tiempo mediante una camilla para evitar daños ópticos. Luego, en el proceso de amplificación, los pulsos acumulan inevitablemente la fase lineal y no lineal que pasa a través de los materiales. Y por último, los pulsos se comprimen en varios tipos de compresores. Para cancelar cualquier orden superior residual en la fase acumulada, generalmente se miden y equilibran las órdenes individuales. Sin embargo, para sistemas uniformes, tal descripción perturbativa a menudo no es necesaria (es decir, propagación en guías de ondas). Los órdenes de dispersión se han generalizado de manera computacionalmente amigable, en forma de transformadas de tipo Lah-Laguerre.
Las órdenes de dispersión se definen por la expansión de Taylor de la fase o el vencedor de ondas. φ φ ()⋅ ⋅ )=φ φ Silencio⋅ ⋅ 0+∂ ∂ φ φ ∂ ∂ ⋅ ⋅ Silencio⋅ ⋅ 0()⋅ ⋅ − − ⋅ ⋅ 0)+12∂ ∂ 2φ φ ∂ ∂ ⋅ ⋅ 2Silencio⋅ ⋅ 0()⋅ ⋅ − − ⋅ ⋅ 0)2+...... +1p!∂ ∂ pφ φ ∂ ∂ ⋅ ⋅ pSilencio⋅ ⋅ 0()⋅ ⋅ − − ⋅ ⋅ 0)p+...... {displaystyle {begin{array}{c}varphi mathrm { {} omega mathrm {)} =varphi left.\right perpetua_{omega ¿Qué? {frac {partial varphi }{partial omega } 'justo en la vida_{omega ¿Por qué? ^{2}varphi }{partial omega ¿Qué? ¿Por qué? +ldots +{frac. {frac {partial ^{p}varphi }{partial omega ¿Qué? ¿Por qué?
k()⋅ ⋅ )=kSilencio⋅ ⋅ 0+∂ ∂ k∂ ∂ ⋅ ⋅ Silencio⋅ ⋅ 0()⋅ ⋅ − − ⋅ ⋅ 0)+12∂ ∂ 2k∂ ∂ ⋅ ⋅ 2Silencio⋅ ⋅ 0()⋅ ⋅ − − ⋅ ⋅ 0)2+...... +1p!∂ ∂ pk∂ ∂ ⋅ ⋅ pSilencio⋅ ⋅ 0()⋅ ⋅ − − ⋅ ⋅ 0)p+...... {displaystyle {begin{rray}{c}kmathrm {} omega mathrm {}} =kleft. ¿Qué? {frac {partial k}{partial omega } 'justo en la vida_{omega ¿Por qué? ¿Qué? ¿Por qué? +ldots +{frac. {fnMicroc {fnK}{partial omega ^{p} {f}justo en la vida_{omega} ¿Por qué?
Las relaciones de dispersión para el olactor k()⋅ ⋅ )=⋅ ⋅ cn()⋅ ⋅ ){displaystyle kmathrm {} omega mathrm {)} ={frac {omega } {c}nmathrm {} omega mathrm {)} } y la fase φ φ ()⋅ ⋅ )=⋅ ⋅ cOP()⋅ ⋅ ){displaystyle varphi mathrm {} omega mathrm {)} ={frac {omega {} {c} {c}m} {fnK} {fnMiega mathrm}} puede expresarse como:
∂ ∂ p∂ ∂ ⋅ ⋅ pk()⋅ ⋅ )=1c()p∂ ∂ p− − 1∂ ∂ ⋅ ⋅ p− − 1n()⋅ ⋅ )+⋅ ⋅ ∂ ∂ p∂ ∂ ⋅ ⋅ pn()⋅ ⋅ )){displaystyle {begin{y}{c}{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {omega }}Kmathrm {} omega mathrm {)} ={frac {1}{c}left(p{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}}} {f}}} {f}} {\fnMicrosoft}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}} {\ {omega } {p-1}}nmathrm {} omega mathrm {)} ################################################################################################################################################################################################################################################################, ∂ ∂ p∂ ∂ ⋅ ⋅ pφ φ ()⋅ ⋅ )=1c()p∂ ∂ p− − 1∂ ∂ ⋅ ⋅ p− − 1OP()⋅ ⋅ )+⋅ ⋅ ∂ ∂ p∂ ∂ ⋅ ⋅ pOP()⋅ ⋅ ))()1){displaystyle {begin{c}{c}{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {omega }}}varphi mathrm { {} omega mathrm {)} ={frac {1}{c}}left(p{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}}} {f}}}} {f}} {\fnMicrosoft}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}} {\ {omega }} {it {}m} {m} omega mathrm {}} {}} {cH00}} {cH00}}} {cH00}}}} {cH00}}}}}} {cH00}}} +omega {frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {omega }} {it {}mathrm {} omega mathrm {)}end{array}}(1)}
Los derivados de cualquier función diferenciable f()⋅ ⋅ Silencioλ λ ){displaystyle fmathrm {} omega mathrm { actual} lambda mathrm {} } en la longitud de onda o el espacio de frecuencia se especifica a través de una transformación de Lah como:
∂ ∂ p∂ ∂ ⋅ ⋅ pf()⋅ ⋅ )=()− − 1)p()λ λ 2π π c)p.. m=0pA()p,m)λ λ m∂ ∂ m∂ ∂ λ λ mf()λ λ ){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} = {} {m} {m}} {m} {}} {m} {f}} {m} {m}} {m} {m} {m}} {m} {m} {cH00}}}} {m} {m} {m} {m}} {m}}}} {mmm}}}}} {m} {mm}}}}} {mmmmmcH00}} {cH00}}}}}}}}}}}}}}}} {m} {mm}} {m}} {mmmmcH00}}}}}}} {cH00}} {cH00} {cH00}}}}}}}}}}}}}}}}} {m}}} ¿Qué? {A}mathrm {} p,mmathrm {}} {m} {m} {m} {m} {m} {m}} {m}} {m}} {m}} {m}} {m} {cH00}}}}} {f} {cHFF}}}}}}}end{array}}}}}}}}}}}}}}} {f}} {m}}}}}}}}}}} {f}}}}} {m}}}}}}} {m}}}} {m}}}}} {m}}} {m}}}}}}}}} {f}}}}} {f}}}} {m}}}} {m}}} {m}}}} {m}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { ,{displaystyle} ∂ ∂ p∂ ∂ λ λ pf()λ λ )=()− − 1)p()⋅ ⋅ 2π π c)p.. m=0pA()p,m)⋅ ⋅ m∂ ∂ m∂ ∂ ⋅ ⋅ mf()⋅ ⋅ )()2){displaystyle {begin{y}{c}{frac} {cHFF} {cH00}} {cH00}} {cHFF}mm} {cH00}} {ccH00} = {cH00} {cH00} {cH00}m} {cH00} {cH00}}} {cH00} {cH00}} {cH00}}}}}}}}}}}}}}}}} {m}ccccccH00} {cH00} {ccH00} {cH00}}}ccH00}}}}}}}ccccH00}}}cH00} {cH00} {cH00}ccH00}ccH00}}cH00}}cH00} {cH00}}}}}cH00}}}cH00}}}}}}c ¿Qué? {A}mathrm {} p,mmathrm {}} {m} {m} {m} {m} {m} {m}} {m} {m} {m}} {m}} {m} {m} {m} {m} {f}m} {f}m}}} {m}}}}} {m}}}} {m}}}}}}} {}}}}}}}}}}}}}}} {m}}}}}}}}}} {m}}}}}}}}}} {m}}}} {m}} {m}}}}}}}}}}}}}}}}}}}}}}}} {m}}} {m}}}} {m}}}} {m}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}} {
Los elementos de matriz de la transformación son los coeficientes Lah: A()p,m)=p!()p− − m)!m!()p− − 1)!()m− − 1)!{displaystyle {mathcal {}mathrm {} p,mmathrm {)} {fnMicroc {fnMicrom} mmathrm {} mmathrm {}} mmathrm {}} {}} {frac {mathrm {} pmathrm {} {}}}}}} {mmathrm {}}}}}}}} {mfnMicrom {m}}}}}}}}} {m}}}}}}} {mmmmmmmmmmmmmmmmmmmcH00cH00cH00cH00cH00cH00cH00}pcH00cH00}pcH00}}}}}}}}}}}cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}}}}}}}}} }{mathrm {} mmathrm {-} mathrm {1)!} }
Escrito para el GDD, la expresión anterior establece que una constante con longitud de onda GGD tendrá cero órdenes superiores. Los órdenes superiores evaluados desde el GDD son:
∂ ∂ p∂ ∂ ⋅ ⋅ pGDD()⋅ ⋅ )=()− − 1)p()λ λ 2π π c)p.. m=0pA()p,m)λ λ m∂ ∂ m∂ ∂ λ λ mGDD()λ λ ){displaystyle {begin{y}{c}{frac} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {omega } {} {} {m}m} {}m} {}}}} {m} {m} {m} {}}m} {}}}}}}} {p} {p} {p} {m} {m} {cH00}}}} {cH00}}}}} {p}}}}} {p}}}}}}}}}m} {p}cccp}p}p}cccp}cccccccccccccccccccp}cccccccccccccccccH00}}}cH00}}cH00}cccH00}}cH00}}ccc ¿Qué? {A}mathrm {} p,mmathrm {}} {lambda } {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} {fnMicrosoft}} {fnMicrosoft}}}} {fnMicrosoft}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { {lambda } {m}}GDDmathrm {} lambda mathrm {}}end{array}}}}}}
Ecuación sustitutiva (2) expresada por el índice refractivo n{displaystyle n} o vía óptica OP{displaystyle ¡Oigan! en la ecuación (1) resultados en expresiones de forma cerrada para las órdenes de dispersión. En general, pth{displaystyle p^{th} Dispersión de orden POD es un tipo Laguerre transformado de orden negativo dos:
POD=dpφ φ ()⋅ ⋅ )d⋅ ⋅ p=()− − 1)p()λ λ 2π π c)()p− − 1).. m=0pB()p,m)()λ λ )mdmOP()λ λ )dλ λ m{displaystyle POD={frac {d^{p}varphi (omega)}{domega ^{p}}=(-1)^{p}({frac {lambda }{2pi c}}}}sum-1)}sum {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicroc {fnMicroc}}} {fnMicros}}}} {fnMicros}} ,{displaystyle}POD=dpk()⋅ ⋅ )d⋅ ⋅ p=()− − 1)p()λ λ 2π π c)()p− − 1).. m=0pB()p,m)()λ λ )mdmn()λ λ )dλ λ m{displaystyle POD={frac {p}k(omega)}{domega ^{p}}=(-1)^{p}({frac {lambda }{2pi c}}}}{(p-1)}sum)} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}} {fnMicroc {fn} {fn}}}}} {fn}}}}
Los elementos de la matriz de los transformados son los coeficientes de orden Laguerre no identificados menos 2, y se dan como: B()p,m)=p!()p− − m)!m!()p− − 2)!()m− − 2)!{displaystyle {mathcal {B}mathrm {} p,mmathrm {)} {fnMicroc {fnMicrom} mmathrm {} mmathrm {}} mmathrm {}} {}} {frac {mathrm {} pmathrm {} pmathrm {2)}}} {mmhm}}}} {mcH00}}}}} {mmmmmcH0} # {mathrm {} mmathrm {-} mathrm {2)} }
Las primeras diez órdenes de dispersión, escritas explícitamente para el vencedor de ondas, son: GD=∂ ∂ ∂ ∂ ⋅ ⋅ k()⋅ ⋅ )=1c()n()⋅ ⋅ )+⋅ ⋅ ∂ ∂ n()⋅ ⋅ )∂ ∂ ⋅ ⋅ )=1c()n()λ λ )− − λ λ ∂ ∂ n()λ λ )∂ ∂ λ λ )=vgr− − 1{begin{}{boldsymbol {it {it}={frac {partial }{partial omega }}kmathrm {} {} {} {} {m} {m} {m}} {mm} {mm}} {mm}m} {mm}m}m} {mm}m}m} {m}m}m} {m}m} {mmm} {m}m}m}m}m} {mmm} {mm}m}mm}}}}m}m} {m}}}} {mm} {mm} {m}m} {m}m} {mmm}m}mm} {m}m} {m}m}m}m}m}m}m}m}m}m} {mm}m} #####omega {frac {partial nmathrm {}omega mathrm {} {} {partial omega }}right)={frac {mathrm {1}c}left(nmathrm {}lambda mathrm {)}}}} -lambda {frac {partial nmathrm {} lambda mathrm {)} {partial lambda }right)=v_{gr}{mathrm {-} mathrm {1}end{array}}
El índice de refracción del grupo ng{displaystyle n_{g} se define como: ng=cvgr− − 1{displaystyle No. {-} mathrm {1}.
GDD=∂ ∂ 2∂ ∂ ⋅ ⋅ 2k()⋅ ⋅ )=1c()2∂ ∂ n()⋅ ⋅ )∂ ∂ ⋅ ⋅ +⋅ ⋅ ∂ ∂ 2n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 2)=1c()λ λ 2π π c)()λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2){fnMicrosoft} {fnMicrosoft}} {fnMicroc {fn} {f} {fn}} {fn}}}} {f}}}} {fn}}}} {fn}}}}}} {f}}}}}}} {f}}}}}}} { {omega }{mathrm {2} kmathrm {} omega mathrm {)} ={frac {mathrm {2} {frac {partial nmathrm {} omega mathrm {} {} {m]} {m2} {m2} {m} {m2}} {m2}} {m2}} {m2} {m2}} {c}} {m2}}}} {m}}}}} {mmm}} {ccccccccccccccccccccccccccccccccc}cccccccccccccccccccc}cccccccccccccccc}ccc} }+omega {frac {partial }{2}nmathrm {} omega mathrm {)} }{partial {omega }{mathrm {2}}}right)={frac {mathrm {1} {} {}}left({frac {lambda }{mathrm {2}pi c}right)left({lambda }{mathrm {2}{frac {partial }nmathrm {} {} {lambda}} {} {c}} {c}} {c}} {c}} {c} {c} {c} {c}c}}}c}c} {c} {c}c} {c}c}c}c}c}c}c}c}c}c}c}ccc}c}cccc}cc}c}cccc}c}c}c}c}c}c}c}c}cc}cc}c}c}c}. {2}}}derecha)end{array}}TOD=∂ ∂ 3∂ ∂ ⋅ ⋅ 3k()⋅ ⋅ )=1c()3∂ ∂ 2n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 2+⋅ ⋅ ∂ ∂ 3n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 3)=− − 1c()λ λ 2π π c)2()3λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3){fnK}= {fnMicrosoft} {fnMicrosoft} {f}} {fn} {f}}} {fnf}} {fnf}}}} {fnfnfnf}}} {fnf} {fnfnKf}f}}}}}}} {f}}}}}}}}}}}}}}\\\\\\\\b}}}}}}}}}}}}}}}\\\\\b}b}}}}}}}}}\\\\\b}}}\\b}}}}}}}}}}\\\\\b}}}}}}}}}}}}}}}}b}}}}}}}}}}}}}}}}}}}}}}}} } {3}{partial {omega }{mathrm {3}} kmathrm {} omega mathrm {)} ={frac {mathrm {1} {}{2}nmathrm {3} {frac {partial }{2}nmathrm {} omega mathrm {}} {} {}} {}} {} {}} {}} {}} {}}} {}} {}}} {}}}}} {}}} {}}}}} {}}}} {}}}}} {}}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}} }{partial {omega. {2}}}+omega {partial } {{3}nmathrm {} omega mathrm {}} }{partial {omega }{mathrm {}}}derecha)={-}{frac {mathrm {fnMicrosoft Sans Serif} {fnMicrom {2} {fnMicrom}}}derecho)}} {mhm} {2}}{Bigl (}mathrm {3} {lambda }{mathrm {2}{frac {partial }{2}nmathrm {} {lambda mathrm {}} {ccccH009} {ccH00} {cH00}}} {ccH00}}} {cH00}}}}}}}} {cccccccccccH00}cccH00}cccccccccccccccH00}cH00}cH00}ccH00}cH00cH00}cH00}}cH00}cH00}ccH00}ccH00}cccH00}ccc. {2}}}+{lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {} {} {fn} {fncipal {lambda. {3}} {Bigr]}end{array}}FOD=∂ ∂ 4∂ ∂ ⋅ ⋅ 4k()⋅ ⋅ )=1c()4∂ ∂ 3n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 3+⋅ ⋅ ∂ ∂ 4n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 4)=1c()λ λ 2π π c)3()12λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+8λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4){fnMicrosoft} {fnMicrosoft} {fnMicrosoft}}= {fnMicroc {fnMicrosoft} {fnMicrosoft}} {f}} {fnMicrosoft} {f}} {f}}}} {f}f}fnMicroc} {f}}}}}} {f}}}}}}}} {\f}}\\\f}f}f}f}f} {f}}}}f}f} {f}}}}}f}f}}}}}}}\f}f}f}f}}b} {b}b} {b}b}}}}}b}b}f}b} {f}}}b}b}}b}b}}b}}}}}}}}}}}}}}}}}} } {4}{partial {omega }{mathrm {4}} kmathrm {} omega mathrm {)} ={frac {mathrm {1} {fn} {fn} {fn} {fn} {fn} {fn} {fnm} {fn} {fn}fn} {fn0}}}fn}}} {fn9}}} {fn0}}}} {fn0}}}}} }{partial {omega }{mathrm {3}}}+omega {partial } {{4}nmathrm {} omega mathrm {}} }{partial {omega }{mathrm {4}}}right)={frac {mathrm {fnMicrosoft Sans Serif} {fnMicrom {2} {fnMicrom}}}derecho)}} {mhm} {3}}{Bigl (}mathrm {12} {lambda }{mathrm {2}{frac {partial }{2}nmathrm {}lambda mathrm {}} {cH00} {ccH009} {ccH00FF}} {cH00}} {cccH00}}}}} {cH00} {ccH00}}}}}}cccccccccccccH00}ccccccccccH00}ccH00} {cH00}ccH00}cccH00}cH00}cH00}cH00}cH00}cH00}ccH00}ccH00} {ccc. {2}}}}+mathrm {8} {lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {}} {cH00} {cH00} {cH00}}} {ccH00}} {cH00}}}}} {cccccccccccccccccH00}cccccH00}cccccccccccccccH00}cH00}ccccccH00}ccccccccH00}cH00}ccH00}ccccccccccc. {3}}}+{lambda }{mathrm {4}{frac {partial }{4}nmathrm {}lambda mathrm {} {} {c]}{partial {lambda. {4}}} {Bigr)}end{array}} {fnMicrosoft Sans Serif}FiOD=∂ ∂ 5∂ ∂ ⋅ ⋅ 5k()⋅ ⋅ )=1c()5∂ ∂ 4n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 4+⋅ ⋅ ∂ ∂ 5n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 5)=− − 1c()λ λ 2π π c)4()60λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+60λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+15λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4+λ λ 5∂ ∂ 5n()λ λ )∂ ∂ λ λ 5){fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}} {fn}}}}} {f}}}}}}}}} {f}}}}}}} { {omega }{mathrm {5} kmathrm {} omega mathrm {)} ={frac {mathrm {1} {}{4}nmathrm {5} {frac {partial }{4}nmathrm {} omega mathrm {}} {}}} {}} {} {}}} {} {}}} {}} {}} {}}} {}}} {}}} {}}}}} {}}}} {}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}}}} }{partial {omega }{mathrm {4}}}+omega {partial } {{5}nmathrm {} omega mathrm {}} }{partial {omega }{mathrm {fnK}}}derecha)={frac {mathrm {fnK} {fnK} {fnK} {fnMicrosoft} {fnK} {fnK}}}}}}} {m} {fnK} {m} {m} {m} {m} {m} {c} {c} {cH00}}} {c}}} {c} {m} {c} {c}c} {c} {c}m} {c} {c} {c}m}m} {c} {c} {c} {c} {c}c}c}c}c}c}c} {c} {c} {c} {c} {c} {c}ccc}c}c}c}c}cc}c}cc}c}c}c}c}c}c}c}. {2}}}}+mathrm {60} {lambda }{mathrm {3}{frac {partial } {}{3}nmathrm {}lambda mathrm {}} {fnuncial {lambda}} {c]} {cH00}} {cH00}}}}} {f}} {f}}}}}}}}}} {ccccccccccccccccccccccccccccccccccccccccccccccccccccccH00}ccccccccccccccH. {3}}}}+mathrm {15} {lambda }{mathrm {4} {frac {partial } {4}nmathrm {}lambda mathrm {}} {cH00} {cH00} {cH00}} {ccH00}}} {ccH00}}}}}} {cccccccccH00cccccH00}ccccccH00}ccccccH00}cccccccccH00cH00}cH00}ccH00}cccccH00}cH00}cH00}cH00cH00}cH00}cccccccc. {4}}}+{lambda }{mathrm {5}{frac {partial }{5}nmathrm {}lambda mathrm {}}} {}}}} {fn}} {fn}}} {fnfnf}}}}}}}} {fnfnfn}}}}}}f}}}}fnfnfnfn}}}fnfnfnfnfn}}}}}fn}fn}fnfnfnf}fnfn}fnfnfnfnfn}}fnfnfnfnfnfnfnfnfn}fnfnfn}}fnfnfnfnfnfnfnfn}}}} ###{partial {lambda. {}}} {Bigr)}end{array}} {fnMicrosoft Sans Serif}SiOD=∂ ∂ 6∂ ∂ ⋅ ⋅ 6k()⋅ ⋅ )=1c()6∂ ∂ 5n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 5+⋅ ⋅ ∂ ∂ 6n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 6)=1c()λ λ 2π π c)5()360λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+480λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+180λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4+24λ λ 5∂ ∂ 5n()λ λ )∂ ∂ λ λ 5+λ λ 6∂ ∂ 6n()λ λ )∂ ∂ λ λ 6){fnMicrosoft} {fnMicrosoft}} {fnMicroc {f} {fn} {fn}} {fn}}} {fn}}}} {fn}}} {fn}}}}}} {f}}}}}} {f}}}}}}}} { {omega }{mathrm {6} kmathrm {} omega mathrm {)} ={frac {mathrm {1}{c}}left(mathrm {6} {frac {partial }{5}nmathrm {}omega mathrm {}} }{partial {omega }{mathrm {5}}}+omega {partial } {{6}nmathrm {} omega mathrm {}} }{partial {omega }{mathrm {6}}}right)={frac {mathrm {fnK} {fnK} {fnK} {fnMicrosoft} {fnK}}}}} {m}}} {fn}} {fn} {fn} {fnK} {fn} {m}} {m} {c} {cH0}} {c}}} {m} {m} {c}} {c}}c} {m} {c}c} {c} {c} {c}m} {c} {c} {c}c} {c}c}}c}c} {c} {c} {c} {c}c} {c}c}c}c}}ccc}c}c}c}c}c}c}c}c}c}c}c}c}c}c}}c}. {2}}}}+mathrm {480} {lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {}} {fn} {cc] {cH009}} {ccH00}cH00}}} {cccH00}}}}}}} {ccccccccccccccccccH00cccccccccccccccccH00cccH00ccH00ccH00ccccccH00cH00cH00}cH00cccccccccccH. {3}}}}+mathrm {180} {lambda }{mathrm {4} {frac {partial }{4}nmathrm {}lambda mathrm {}} {cH00} {cH00} {cH00}} {ccH009}} {cH00}}}}} {ccccH00}}}}}}} {ccccccccccccccccccccccccccccccccccH00}cccccccccccccccH00}cH00}ccH00cccccccccccH. {4}}}}+mathrm {24} {lambda }{mathrm {5} {frac {partial }{5}nmathrm {}lambda mathrm {}}}}} {fn}}} {fnfnf}}}}fnfnfnfnfnfnfnfn}}fnfnfnfnfnfnfnfn}fnfn}fn}fnfnfn}fnfnfnfnfnfnfnfnfnfnfn}fnfnfnfn}fnfnfnfnfnfnfnfn}fnfnfnfnfn}fnfn}fnfn ###{partial {lambda. {5}}}}+{lambda }{mathrm {6}{frac {partial }{6}nmathrm {}lambda mathrm {} {}}{partial {lambda. {6}} {Bigr]}end{array}}SeOD=∂ ∂ 7∂ ∂ ⋅ ⋅ 7k()⋅ ⋅ )=1c()7∂ ∂ 6n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 6+⋅ ⋅ ∂ ∂ 7n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 7)=− − 1c()λ λ 2π π c)6()2520λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+4200λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+2100λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4+420λ λ 5∂ ∂ 5n()λ λ )∂ ∂ λ λ 5+35λ λ 6∂ ∂ 6n()λ λ )∂ ∂ λ λ 6+λ λ 7∂ ∂ 7n()λ λ )∂ ∂ λ λ 7){fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicroc {fnMicrosoft} {fn}}} {f}}}} {fnMicrosoft} {fn}}}} {f}}}}}}} {f}}}}}} {f}}}}}} { {omega }{mathrm {7} kmathrm {} omega mathrm {)} ={frac {mathrm {1} {}{6}nmathrm {7} {frac {partial }{6}nmathrm {} omega mathrm {}} {} {}} {}} {}} {} {}}} {c}} {c}} {c} {c}}}}}c}}}} {c}}c}}}}}}}}c}}}c}c}c}c}c}c}c}c}c}c}c}cc}c}c}c}ccc}c}c}c}c}c}c}c}c}c}c}c}c}c}cc}cc}c}c}c}c}c}c}c}c}c}c}c}c}c}c} }{partial omega. {6}}}+omega {partial } {{7}nmathrm {} omega mathrm {}} }{partial omega. {7}}}right)={-}{frac {mathrm {fnMicrosoft Sans Serif} {fnMicrom {2} {fnMicrom}}}derecho)}} {mhm} {6} {Bigl (}mathrm {2520} {lambda }{mathrm {2}{frac {partial }{2}nmathrm {} {lambda mathrm {}} {c] {ccH009} {ccH009} {cH00}}} {cH00}} {cH00}}}}}}}}}} {cccccccccccccccH00}ccH00}ccH00}cccccccH00}cH00cH00}cH00}cH00}cccH00}cH00}cH00}cH00}cH00}cH00}ccH00}ccH00}}}ccH. {2}}}}+mathrm {4200} {lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {}} {fn} {cc] {cH009}} {ccH00}cH00}}}} {ccccH00}}}}}}} {cccccccccccccccccccccccccccccccccccH00ccccccH00}ccH00cccH00}cH00}cH00}cH00ccccccccccccH. {3}}}}+mathrm {2100} {lambda }{mathrm {4}{frac {partial }{4}nmathrm {}lambda mathrm {}} {cH00} {cccH009}} {ccH009}} {cH00}}}} {ccccH00}}}}}}}}}} {cccccccccccccccccccccccccccccccccccccccccccH00cccccH00cH00cH00}cH00cccccccccccH. {4}}}}+mathrm {420} {lambda }{mathrm {5} {frac {partial }{5}nmathrm {}lambda mathrm {}} {cH00} {cccH009}} {ccH009}} {cH00}}}}} {ccccccccccH00ccccccH00}cccccH00}cccH00}cccccccccccH00}cH00}ccH00}cH00}ccH00cccH00}cH00}ccH00}cH00ccccccccH00}ccH. {5}}}}+mathrm {35} {lambda }{mathrm {6}{frac {partial } {6}nmathrm {}lambda mathrm {}} {cH00} {cH00} {cH00}} {ccH00}}} {ccH00}}}}}} {cccccccccH00}ccccccccccccccccH00}ccccccccccccH00cH00}cH00}ccH00}ccccccH00}cH00}ccH00}cH00}cccccccH00}ccH. {6}}}+{lambda }{mathrm {7}{frac {partial }{7}nmathrm {}lambda mathrm {} {} {c]}{partial {lambda. {7}} {Bigr]}end{array}}EOD=∂ ∂ 8∂ ∂ ⋅ ⋅ 8k()⋅ ⋅ )=1c()8∂ ∂ 7n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 7+⋅ ⋅ ∂ ∂ 8n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 8)=1c()λ λ 2π π c)7()20160λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+40320λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+25200λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4+6720λ λ 5∂ ∂ 5n()λ λ )∂ ∂ λ λ 5+840λ λ 6∂ ∂ 6n()λ λ )∂ ∂ λ λ 6++48λ λ 7∂ ∂ 7n()λ λ )∂ ∂ λ λ 7+λ λ 8∂ ∂ 8n()λ λ )∂ ∂ λ λ 8){fnMicrosoft} {fnMicrosoft}} {fnMicrosoft} {fn}} {f}} {f}}}}} {fn}}}} {fn}}}}} {fn}}}}}}} {f}}}}}}}} { {omega }{mathrm {8} kmathrm {} omega mathrm {)} ={frac {mathrm {1} {fn} {fn}m} {fn} {fn} {fnfn} {fnm} {fn} {fn}fn}} {fn}fn} {fn} {fnfn}} {fn}}}fn}}}}} {fn}}} }{partial omega. {7}}}+omega {partial } {{8}nmathrm {} omega mathrm {}} }{partial {omega }{mathrm {8}}}right)={frac {mathrm {fnMicrosoft Sans Serif} {fnMicrom {2} {fnMicrom}}}derecho)}} {mhm} {7}{Bigl (}mathrm {20160} {lambda }{mathrm {2}{frac {partial }{2}nmathrm {}lambda mathrm {}} {cH00} {cH00}} {ccH009}} {cH00}}}} {cccH00}}}}}}}}}} {ccccccccccccccccH00ccH00}cccH00}cccccccH00}cH00}cH00}cccH00}cH00cH00}cH00}cH00}cH00}cH00}cH00}cH00}cccH00}}ccH. {2}}}+mathrm {40320} {lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {}}}{lambda {}} {lambda {c}}}} {cH00}}} {ccccccH00}}}}}}}}}}}} {cccccccccccccccccccccccccccccccccccccccccccccccccccH00}cH00}cH00cccccccccccc. {3}}}}+mathrm {25200} {lambda }{mathrm {4}{frac {partial }{4}nmathrm {}lambda mathrm {}} {cH00} {cccH009}} {ccH009}} {cH00}}}} {ccccH00}}}}}}} {ccccccccccccccccH00ccccccccccccccccH00cH00}cH00}ccH00}ccH00ccccccH00}cH00}ccH00}ccccccccccH. {4}}}}+mathrm {6720} {lambda }{mathrm {5} {frac {partial }{5}nmathrm {}lambda mathrm {}}}}}} {fn}}} {fnf}}} {fnfnfnfn}fnfn}}fn}}}}fnfnfnfnfnfnfnfnfnfn}fnfnfn}fn}fnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfnfnfnfnfn}fnfnfn}fnfn}fnfn}fnfnfn}}fn ###{partial {lambda. {5}}}}+mathrm {840} {lambda }{mathrm {6}{frac {partial }{6}nmathrm {}lambda mathrm {}} {cH00}} {cccH009}} {ccH009}} {cH00}}}}} {ccccccccccH00}ccccccccccccH00}ccccccH00}cccccccccH00cH00}cH00}ccH00}ccccccccH00}cH00}cH00ccccccccccccH. {6}}}\\\\\\m} {c} {fn} {fn} {fn} {fnfn} {fnfnm} {fnfnfnfn} {fnfn}} {fnfnMicrom {fn}}} {fn}}}}} {\\fnfn\fnfnfnfnMicrom} {fnfn}}}}fnfnfn}}}\fnfn\\\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfn}fn}fnfnfnfnfnfnfnfn\fn. {7}}}+{lambda }{mathrm {8}{frac {partial }{8}nmathrm {}lambda mathrm {}}} {}}} {}}} {fnfn}}} {fnfnf}}}}}}}} {fnfnfn}}}}}}f}}}fnfn}fnfn}}fnfnfn}fn}fn}}}fn}fn}fn}fnfn}}}fnfn}fnfnfn}}fnfn}fnfnfnfnfnfnfnfnfnfnfn}fn}}fnfnfnfnfnfnfn}}}}}} ###{partial {lambda. {8}}} {Bigr)}end{array}} {fnMicrosoft Sans Serif}NOD=∂ ∂ 9∂ ∂ ⋅ ⋅ 9k()⋅ ⋅ )=1c()9∂ ∂ 8n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 8+⋅ ⋅ ∂ ∂ 9n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 9)=− − 1c()λ λ 2π π c)8()181440λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+423360λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+317520λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4+105840λ λ 5∂ ∂ 5n()λ λ )∂ ∂ λ λ 5+17640λ λ 6∂ ∂ 6n()λ λ )∂ ∂ λ λ 6++1512λ λ 7∂ ∂ 7n()λ λ )∂ ∂ λ λ 7+63λ λ 8∂ ∂ 8n()λ λ )∂ ∂ λ λ 8+λ λ 9∂ ∂ 9n()λ λ )∂ ∂ λ λ 9){fnK} {fn} {fnK}}= {fnK} {f}} {f}} {fn}} {fnf}} {fnfn}}}} {fnf}}} {fnfnf}f}}}}}}}}}} {b}}}}}}}}}}}}} {m}}}}}}}}}b} {m}}\b} {b}b}b}b}b}b}}b}}}}}}b}b}}}}}}}}}}}}b}b} {b} {b}b}}}}}b}}}}}b}}}}b}b}b}}}}}b}}}}}b}}}}}}}}}}}}}}}}}}}}}}}} } {9}{partial {omega }{mathrm {9} kmathrm {} omega mathrm {)} ={frac {mathrm {1} {} {} {} {} {m} {}m} {m}mm} {}mmm} {}mm} {} {}} {cHFF} {}}}}} {fn}}} {c}}} {c}}} {c}}}}} {c}}}}} {c}}}}}}}} {c}}}}}}}}c}}}}}}}c}}}c}}}}}}}cccccc}c}ccccc}c}c}c}c}c}c}c}ccc}c}c}cccc}c}c}c}c}c}c}c}c}cc}c}c}c}c}c} }{partial {omega. {8}}}+omega {partial } {{9}nmathrm {} omega mathrm {)} {} {partial} {} {} {}}} {fn} {fn}} {fn0}}}} {fn}}}}}} { {omega }{mathrm {}}}derecha)={-}{frac {mathrm {fnMicrosoft Sans Serif} {fnMicrom {2} {fnMicrom}}}derecho)}} {mhm} {8}}{Bigl (}mathrm {181440} {lambda }{mathrm {2}{frac {partial }{2}nmathrm {} {lambda mathrm {}}} {Lambdam} {]} {cH009} {cH00}} {cH00}}}}}}}}}}} {cccccccccccccccccccH00}ccH00}cccccccccccH00}cH00}ccH00}ccH00}ccH00}ccH00}cH00}cH00}cH00cH00}ccH00}ccH00}cccH. {2}}}}+mathrm {423360} {lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {}} {fnuncial {lambda}}}} {m}} {ccH00}}} {ccccH00}}}}}}}}}}}} {ccccccccccccccccccccccccccccccccccH00ccccccH00ccccccccccH00cH00ccH00cccccccccccc. {3}}}}+mathrm {317520} {lambda }{mathrm {4}{frac {partial }{4}nmathrm {}lambda mathrm {}} {fn} {cc] {cH002}} {ccH009} {cH00}}}}} {ccccccH00}}}}cccccccccccccccH00cccccccccccccccH00}cH00}cccccH00}ccccccccH00}cH00}ccH00cccccccH004cccH. {4}}}}+mathrm {105840} {lambda }{mathrm {5}{frac {partial }{5}nmathrm {}lambda mathrm {}} {fn} {fn} {ccccH004}}} {ccH00}}}}} {ccccccccccH00ccccccH00}cccccccccccccH00}cccccccccH00cccccccH00}cH00cccH00}ccH00}cH00}cH00cccccccccccc. {5}}}}+mathrm {17640} {lambda }{mathrm {6}{frac {partial }{6}nmathrm {} {lambdamathrm {}} {fn}} {m} {cc]} {cccH009cH00}} {cccH00}}}}}}}}}} {ccccccccccccccccH00cccccccH00cccccccH00}cH00ccH00cccH00cccH00cH00cH00}cH00}cH00}cH00cccccccH004cccH. {6}}}\\\\\\\\m} {cH00} {mm} {mm} {mm} {cccHFF} {mcHFF} {cH00} {cH00FF}} {cH00}cH00} {cH00}cH00} {cH00}}}}}}}}}} {ccH00}}}}}ccccccccccH00}cH00ccccH00}cH00}ccccH00}cH00}cH00}cH00}cH00}cH00cccH00}cH00}cH00}cH00}cH00}ccH00}ccH00}cccH. {7}}}}+mathrm {63} {lambda }{mathrm {8}{frac {partial } {8}nmathrm {}lambda mathrm {}}}}}} {fn}}} {fnfn}}}}} {fnfnfnfnfnfn}fn}}fnfnfnfnfnfnfnfnfnfn}fn}fnfn}fnfnfnfnfnfnfn}fn}fnfnfnfn}fnfnfnfnfnfnfnfnfnfnfnfnfn}fnfnfnfn}fnfnfn}fn ###{partial {lambda. {}}}+{lambda}{mathrm {9}{frac {f} {m} {m} {m} {f}}} {f}}}}} {fn}}}}}}}}}\\mcccccccccccccccccH00cccccccccccccH00ccccH00ccccccccccccccccccH00ccccccccccccccccccH00cH00cH00ccH00cccccc\\cH00 }{9}nmathrm {} lambda mathrm {)}{partial {lambda. {}}} {Bigr)}end{array}}TeOD=∂ ∂ 10∂ ∂ ⋅ ⋅ 10k()⋅ ⋅ )=1c()10∂ ∂ 9n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 9+⋅ ⋅ ∂ ∂ 10n()⋅ ⋅ )∂ ∂ ⋅ ⋅ 10)=1c()λ λ 2π π c)9()1814400λ λ 2∂ ∂ 2n()λ λ )∂ ∂ λ λ 2+4838400λ λ 3∂ ∂ 3n()λ λ )∂ ∂ λ λ 3+4233600λ λ 4∂ ∂ 4n()λ λ )∂ ∂ λ λ 4+1693440λ λ 5∂ ∂ 5n()λ λ )∂ ∂ λ λ 5++352800λ λ 6∂ ∂ 6n()λ λ )∂ ∂ λ λ 6+40320λ λ 7∂ ∂ 7n()λ λ )∂ ∂ λ λ 7+2520λ λ 8∂ ∂ 8n()λ λ )∂ ∂ λ λ 8+80λ λ 9∂ ∂ 9n()λ λ )∂ ∂ λ λ 9+λ λ 10∂ ∂ 10n()λ λ )∂ ∂ λ λ 10){fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnMicroc {fnMicrosoft} {f}}} {f}}}} {fnMicrosoft}} {f}}}}} {f}}} {f}}}}}}}}} {f}}}}}}}}} { {omega }{mathrm {}} kmathrm {} omega mathrm {}} ={frac {mathrm {1} {fn} {fn}m} {fnK} {fn} {fn} {fnm} {fn} {fn}} {fn}} {fn}} {fn}} {\fnfnfn}}}} {fnfnc}}}} {f}}} {fn}}}}}}}}}}}} {\\\\\\fnp}fn}}\\p}\p}c}p}p}c}}\\\\\\c} {c} {c}}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}}c}c} {omega. {9}}}+omega {partial } {{10}nmathrm {} omega mathrm {}} {fncipal {omega } {mh00}}}derecha)={frac {mathrm {fn} {fn} {fnK} {fnK}}} {m} {m}}}}}} {m}}}} {m} {fn}} {m} {m} {m} {m} {m} {m}} {m} {cH0}}}} {m} {c} {m} {c} {c}}}} {c}} {c}}}}} {c} {c}m}m} {c} {c} {c}c}}}}}c}}}}}}}}} {c} {c} {c} {c}}}} {cc}}}c}}}}}ccc}c}}}}}c}}}}}}}}}}ccc}ccccc}}}}}}c}. {2}}}+mathrm {4838400} {lambda }{mathrm {3}{frac {partial }{3}nmathrm {}lambda mathrm {}}}{lambda {}} {lambda {c}}}} {cH00}}}} {cccccH00}}}}}}}}}}}}}} {ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccH. {3}}}}+mathrm {4233600} {lambda }{mathrm {4}{frac {partial }{4}nmathrm {}lambda mathrm {}} {fnuncial {lambda} {fn}}}} {ccH00} {fn}}}}}} {f}}}}} {f}}}\\cccccccccccccccH00ccccccccccccccH00ccH00cH00}ccccH00ccccccccH00cH00cH00}cH00cccccccH00}cccH. {4}}}}+{1693440}{lambda }{mathrm {5}{frac {partial }{5}nmathrm {}lambda mathrm {}}}}}} {fn}}} {fnfn}} {fn}} {fnf}}fnfnf}}fnfn}fnfn}fnfn}fnfn9}fnfnfn}fnfnfn}fnfn}fnfnfnfnfnfnfn}fn9}fnfnfnfnfn}fnfnfnfnfnfnfn}fn}fnfnfnfn}fnfn}fn}fnK ###{partial {lambda. {5}}}\\\\\\m2800} {lambda }{mathrm {6}{frac {partial }{6}nmathrm {}lambda mathrm {}} {cccH00} {ccH00} {cH00} {cH00}}}} {cH00}}}}}}}}} {ccccccccccccccccH00cccH00}ccccccccccH00}cH00cH00}cH00}ccH00}cH00cccH00}ccH00}cH00}ccH00}ccH00}ccH00}cccH. {6}}}}+mathrm {40320} {lambda }{mathrm {7}{frac {partial }{7}nmathrm {}lambda mathrm {}} {fnuncial {lambda}}} {c]} {ccH00}} {cH00}}}}}} {cccccccccccccccccccccccH00cccccccH00cccccccH00}cH00ccH00cccH00}cH00cccccH00cH00}cH00}cH00cccccccH00}cccH. {7}}}}+mathrm {25} {lambda }{mathrm {8}{frac {partial }{8}nmathrm {}lambda mathrm {}}}}} {fn}}} {fnfnf}}}fnfnfnfn}}fnfnfnfn}fnfnfnfn}fnfnfn}fnfn}fnfnfnfnfnfn}fnfn}fnfnfn}fnfnfnfn}fnfn}fnfnfnfnfnfnfnfnfnfnfn}fnfnfnfnfnfnfnfnfn ###{partial {lambda. {8}}}}+mathrm {80} {lambda }{mathrm {9}{frac {partial }{9}nmathrm {}lambda mathrm {}} {cH00} {cH00} {cH009}} {cH00}}} {ccH00}}}}}} {ccccccccccccccccH00}cccccccccH00}ccccccccccccccH00}cH00cccH00}ccH00cccH00}cH00}cH00}ccH00}ccccccH00}cccH. {9}}}+{lambda }{mathrm {10}{frac {partial }{10}nmathrm {}lambda mathrm {}} {m}}{partial {lambda {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}
Explícitamente, escrita para la fase φ φ {displaystyle varphi }, las primeras diez órdenes de dispersión se pueden expresar como una función de longitud de onda utilizando los transformados Lah (ecuación (2)) como:
∂ ∂ p∂ ∂ ⋅ ⋅ pf()⋅ ⋅ )=()− − 1)p()λ λ 2π π c)p.. m=0pA()p,m)λ λ m∂ ∂ m∂ ∂ λ λ mf()λ λ ){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} = {} {m} {m}} {m} {}} {m} {f}} {m} {m}} {m} {m} {m}} {m} {m} {cH00}}}} {m} {m} {m} {m}} {m}}}} {mmm}}}}} {m} {mm}}}}} {mmmmmcH00}} {cH00}}}}}}}}}}}}}}}} {m} {mm}} {m}} {mmmmcH00}}}}}}} {cH00}} {cH00} {cH00}}}}}}}}}}}}}}}}} {m}}} ¿Qué? {A}mathrm {} p,mmathrm {}} {m} {m} {m} {m} {m} {m}} {m}} {m}} {m}} {m}} {m} {cH00}}}}} {f} {cHFF}}}}}}}end{array}}}}}}}}}}}}}}} {f}} {m}}}}}}}}}}} {f}}}}} {m}}}}}}} {m}}}} {m}}}}} {m}}} {m}}}}}}}}} {f}}}}} {f}}}} {m}}}} {m}}} {m}}}} {m}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { ,{displaystyle} ∂ ∂ p∂ ∂ λ λ pf()λ λ )=()− − 1)p()⋅ ⋅ 2π π c)p.. m=0pA()p,m)⋅ ⋅ m∂ ∂ m∂ ∂ ⋅ ⋅ mf()⋅ ⋅ ){displaystyle {begin{y}{c}{frac} {cHFF} {cH00}} {cH00}} {cHFF}mm} {cH00}} {ccH00} = {cH00} {cH00} {cH00}m} {cH00} {cH00}}} {cH00} {cH00}} {cH00}}}}}}}}}}}}}}}}} {m}ccccccH00} {cH00} {ccH00} {cH00}}}ccH00}}}}}}}ccccH00}}}cH00} {cH00} {cH00}ccH00}ccH00}}cH00}}cH00} {cH00}}}}}cH00}}}cH00}}}}}}c ¿Qué? {A}mathrm {} p,mmathrm {}} {omega }{m}{frac {partial }{m}{partial {omega } {m}} {m}} {m} {m} {m} {m}} {m}}} {m}} {m}} {m}} {m}}}}}m} {m}}}}} {m}}}}} {m}}}}}} {m}}} {m}}}}}}} {m}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}} {m}} {m}}} {f} {m} {f}} {m}}}}}}}}}}}}} {m} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m} {m} { }end{array}}
∂ ∂ φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ =− − ()2π π c⋅ ⋅ 2)∂ ∂ φ φ ()⋅ ⋅ )∂ ∂ λ λ =− − ()λ λ 22π π c)∂ ∂ φ φ ()λ λ )∂ ∂ λ λ {displaystyle {begin{array}{frac {partial varphi mathrm { {} omega mathrm {}} {partial omegaega }={-}left({frac {mathrm {2}pi c}{omega }{mathrm {2}}}}}right){frac {partial varphi mathrm { {}omega mathrm {}}}} {partial lambda }={-}left {frac {lambda }{mathrm {2}}{mathrm {2}pi c}right){frac {partial varphi mathrm {} {lambda mathrm {)}}} {ccccH002}} {c]} {ccc]}ccccccccH00cccccccH00cH00cccH00}ccH00}cccH00}cccccccH00}ccH00}}}}cccH00}ccH00ccH00}ccH00}}cH00}}cH00}cccH00}cH00}}}ccc }end{array}}
∂ ∂ 2φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 2=∂ ∂ ∂ ∂ ⋅ ⋅ ()∂ ∂ φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ )=()λ λ 2π π c)2()2λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2){displaystyle {begin{}{frac {{partial }varphi mathrm {}omega mathrm {} {}}{partial}} { {omega. {} {m} {m}} {m}m} {m}m}}} {m} {m} {m} {m}}m} {ccH0}} {m}cH0} {cH00}}} {m} {ccH00}cH00} {cH0}}}cH00}}cH0}}}}cccH00}cccH00} {cH00} {cH00} {ccH00}cH00}cH00}cH00}}}}}}ccccH00}ccH00}cH00} {cH00}cH00}}cH00}cH00}}}cH00}cH00}cH00}cccH00}cH00}}}}}}}}cH }+{lambda }{mathrm {2} {fnMicroc {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f}} {fnMicroc} {fnMicrosoft} {fnMicrosoft}} {fnMicroc {fnMicroc} {fnMicroc}}} {fnMicroc} {f} {f}}}} {f}f}}}}}f}f}f} {\f}f}f}f}f}f}f}fnMicroc}f}f}f}f}f}f}fnMicroc} {fnMicroc {fnMicroc {\\\\\f}fnMicroc}\f}fnMicroc}}\fnMicroc}\\\\f}}}}}}}fn }{2}varphi mathrm { {} lambda mathrm {)}{partial {lambda. {2}}}derecha)end{array}}
∂ ∂ 3φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 3=− − ()λ λ 2π π c)3()6λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +6λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3){displaystyle {begin{rray}{frac {{partial }varphi mathrm {}omega mathrm {}} }{partial {omega. {3}}={-}{eft({frac {lambda }{mathrm {2}pi c}right)}}}{mathrm {3}left(mathrm {6} lambda {frac {partial varphimathrm {} {} {lambda mathrm} {} {}} {} {} {} {}}} {}}}}} {}}} {}}}}}}} {}} {} {} {} {}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}} {} {} {}}}}}}} {}}}} {}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}} { }+mathrm {6} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}+{lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {} lambda mathrm {} {} {c]} {ccH0} {c]} {ccccH004cH009}cH00}}}} {cH00}}}}}}}ccccccccccccccccccH00}cccccccccccccccccH3}ccccccH00ccH00cccH00}cH00cH004cH004cH004ccH004ccH004cccH. {3} {}}}derecha)end{array}}
∂ ∂ 4φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 4=()λ λ 2π π c)4()24λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +36λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+12λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4){displaystyle {begin{}{}{frac {partial }varphi mathrm {} {}omega mathrm {}} {} {partial}} {c} {cH00}}} {cHFF}}} {cH00}}}}}} { {omega }{mathrm {4}}={left({frac {lambda }{mathrm {2}pi c}right)}}{mathrm {4} {Bigl (}mathrm {24}lambda {frac {partial varphimathrm {}{} {lambda mathrm} {} {}} {} {}}}} {}}}}}}}}} {m} {cc}}}}ccccccccccccccccccccccccccccccccccccccccccccccccc}ccH00}ccH00}}ccccccc }+mathrm {36} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}}+mathrm {12} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {}lambda mathrm {}} {fnuncio {c]} {ccccH002}}} {cH00}}}}} {cccccccccccH00ccccccccccccH00cccccccH00cccccccccH00cH00}cH00}ccH00}ccH00ccH00}ccH00}cH00}cH00ccccccccccccH. {3}}}+{lambda}{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}} {Bigr)}end{array}} {fnMicrosoft Sans Serif}∂ ∂ 5φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 5=− − ()λ λ 2π π c)5()120λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +240λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+120λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+20λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4+λ λ 5∂ ∂ 5φ φ ()λ λ )∂ ∂ λ λ 5){displaystyle {begin{}{l}{frac} {{partial }{mathrm {5}varphi mathrm {} omega mathrm {)} }{partial {omega }{mathrm {fnK} {fnK}} {fnMicroc {lambda }{mathrm {2}pi c}}right)}}{mathrm}}}} {m}}}}}} {m}}}}}}} {m} {m}}}}}}}}}} {m}}}}} {m}}}}}}} {m}}}}} {m}}}}}}}} {m} {m} {m}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m} {m}}}}}}}}}}}}}}}}}} {m}}} {m}} {m}}}}}}}}}}}}}}}}}} {m}}}}}} {5} }{Bigl (}mathrm {120} lambda {frac {partial varphi mathrm {} lambda mathrm {}} {partial lambda }+mathrm {240} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}}+mathrm {120} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {}lambda mathrm {}} {fnuncio {c]} {fnuncial {cH002}}}}} {cccccH00}}}}}}} {cccccccccccccccccccccccccccH00cccccccccH00ccccccH00ccH00ccccccH00}cH00}cccccccccH004cccc. {3}}}+mathrm {20} {lambda}{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}}+{lambda }{mathrm {5}{frac {partial }{5}varphi mathrm {}lambda mathrm {} {} {c]}{partial {lambda. {}}} {Bigr)}end{array}} {fnMicrosoft Sans Serif}∂ ∂ 6φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 6=()λ λ 2π π c)6()720λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +1800λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+1200λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+300λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4+30λ λ 5∂ ∂ 5φ φ ()λ λ )∂ ∂ λ λ 5+λ λ 6∂ ∂ 6φ φ ()λ λ )∂ ∂ λ λ 6){displaystyle {begin{rray}{frac {partial }varphi mathrm {}omega mathrm {} {cHFF} {cHFF} {cHFF} {cHFF} {cH00}}} {cHFF}}} {cHFF}}} {b}}}}}} { {omega }{mathrm {6}}={frac {lambda }{mathrm {2}i}right)}}{mathrm} {i}}}}} {m}}}} {m}}}}}} {m}}}}} {m}}} {m}}}}}}}}} {m}}}}}}}}} {m} {m}}}}}}}} {m}}}} {m}} {m} {m} {m}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m} {m}} {m}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}} {6} }{Bigl (}mathrm {720} lambda {frac {partial varphi mathrm {} lambda mathrm {} {} {partial lambda }+mathrm {1800} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}}+mathrm {1200} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {}lambda mathrm {}} {fnuncio {c]} {cccH002}} {cH00}}}}}} {cccccccccccccccccccccccccH00ccccccH00}cccccccccccH00}cccccH00}cH00cccH00}ccH00}cH00}cccccccccH00}cccH. {3}}}+mathrm {300} {lambda}{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}}}+mathrm {30} {lambda }{mathrm {5} {frac {partial }{5}varphi mathrm {}lambda mathrm {}} {fnuncio {c]} {ccccH004}}} {ccH00cH00}}}}}}}} {ccccccccccccccccccccH00cccccccH00cccccccccH00ccH00cccH00ccH00ccccccH00ccH004}cH00cccccccH004}ccc. {5}}}mathrm {} {lambda }{mathrm {6}{frac {partial }{6}varphi mathrm {} lambda mathrm {} {cc]}{partial {lambda. {6}} {Bigr]}end{array}}∂ ∂ 7φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 7=− − ()λ λ 2π π c)7()5040λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +15120λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+12600λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+4200λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4+630λ λ 5∂ ∂ 5φ φ ()λ λ )∂ ∂ λ λ 5+42λ λ 6∂ ∂ 6φ φ ()λ λ )∂ ∂ λ λ 6+λ λ 7∂ ∂ 7φ φ ()λ λ )∂ ∂ λ λ 7){displaystyle {begin{rray}{frac {partial }varphi mathrm {}omega mathrm {}} {partial} {fnuncio}} {fnuncio}} {fnuncio}} {fnuncio}}}}} { {omega. {7}}={left({frac {lambda }{mathrm {2}pi c}}right)}{mathrm}}}}} {m}}} {m}}}}} {m}}}}}} {m}} {m}}}}} {m}}}}}}}}}}}}} {m}} {m}}}}}}}} {m}}} {m}}}}} {m} {m} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m} {m} {m} {m}}}}}}} {m}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}} {7} }{Bigl (}mathrm {5040} lambda {frac {partial varphi mathrm {} lambda mathrm {} {} {partial lambda }+mathrm {15120} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}+mathrm {12600} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {} {lambda mathrm {}} {fnuncio {c]} {cccH002}} {cH00}}}}} {ccccccccccccH00ccccccccccccH00cccccccH00}cccccccccH00cH009cH00}cH00}ccH00ccccccH00}cH0}ccH004ccH004cccccccH. {3}}}+mathrm {4200} {lambda}{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}}+mathrm {630} {lambda}{mathrm {5}} {frac {partial } {5}varphi mathrm { {} lambda mathrm {}} {ccH00}} {cambial {lambda. {5}}}+mathrm {42} {lambda}{mathrm {6} {fn} {c}varphi mathrm {} lambda mathrm {}} {ccH00} {cH00} {ccH0} {cH0}} {ccH00}} {ccH009}}}} {cH00cH00}}} {cccH00}}}}} {cH00}}}}}ccccccccH00}cccccH00}ccH00}ccH00}}cH00}ccccH00}ccH00}cH00}cccH00}ccH00}ccH00}cH00}cH00}cccH00}ccH00}ccH00}cccH. {6}}}+{lambda }{mathrm {7}{frac {partial }{7}varphi mathrm {} lambda mathrm {} {} {c]} {ccH0} {c]} {cH0} {ccH00}cH00}cH00}}}}} {cH00}}}}}}}}}} {ccccccccccccccccccccccccccccccccccH00ccccccH00}cccccH00}ccH00}cH00}ccccccccccH00}ccc. {7}} {Bigr]}end{array}}∂ ∂ 8φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 8=()λ λ 2π π c)8()40320λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +141120λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+141120λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+58800λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4+11760λ λ 5∂ ∂ 5φ φ ()λ λ )∂ ∂ λ λ 5+1176λ λ 6∂ ∂ 6φ φ ()λ λ )∂ ∂ λ λ 6+56λ λ 7∂ ∂ 7φ φ ()λ λ )∂ ∂ λ λ 7++λ λ 8∂ ∂ 8φ φ ()λ λ )∂ ∂ λ λ 8){displaystyle {begin{}{frac {{partial }varphi mathrm {}omega mathrm {}} {partial} {} {fnuncio}}} {fnuncio}} {fn}} {fnuncio}}}}} { {omega. {}}={frac {lambda }{mathrm {2}i}derecha)}}{mathrm {8} }{Bigl (}mathrm {40320} lambda {frac {partial varphi mathrm {} lambda mathrm {} {}{partial lambda }+mathrm {141120} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}+mathrm {1420} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {} {lambda mathrm {}} {fnuncio {c]} {cccH002} {cH00}}}} {ccccH00}}}}} {cccccccccccH00cccH00cccH00ccH00ccccH00ccccH00cH00}cH00cH00}cH00}cH00cccH00ccccH00cH00}cH00}cH00cccccccccccc. {3}}}+mathrm {58800} {lambda}{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}}+mathrm {11760} {lambda }{mathrm {5}} {frac {partial } {5}varphi mathrm { {} lambda mathrm {}} {ccH00}} {cambial {lambda. {5}}}+mathrm {1176} {lambda}{mathrm {6} {fn} {c}varphi mathrm {} lambda mathrm {}} {ccH00} {cH00} {ccH0} {cH0}} {ccH00}} {ccH009}}}} {cH00cH00}}} {cccH00}}}}} {cH00}}}}}ccccccccH00}cccccH00}ccH00}ccH00}}cH00}ccccH00}ccH00}cH00}cccH00}ccH00}ccH00}cH00}cH00}cccH00}ccH00}ccH00}cccH. {6}}}+mathrm {56} {lambda}{mathrm {7} {fn} {fnK}varphi mathrm {} lambda mathrm {}}} {cluido {fn]} {fnuncial {lambda. {7}}}+\+{lambda }{mathrm {8}{frac {partial ^{8}varphi mathrm {}lambda mathrm {} {}}{partial {lambda. {8}}} {Bigr)}end{array}} {fnMicrosoft Sans Serif}∂ ∂ 9φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 9=− − ()λ λ 2π π c)9()362880λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +1451520λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+1693440λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+846720λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4+211680λ λ 5∂ ∂ 5φ φ ()λ λ )∂ ∂ λ λ 5+28224λ λ 6∂ ∂ 6φ φ ()λ λ )∂ ∂ λ λ 6++2016λ λ 7∂ ∂ 7φ φ ()λ λ )∂ ∂ λ λ 7+72λ λ 8∂ ∂ 8φ φ ()λ λ )∂ ∂ λ λ 8+λ λ 9∂ ∂ 9φ φ ()λ λ )∂ ∂ λ λ 9){displaystyle {begin{}{frac {{partial }varphi mathrm {}omega mathrm {} {}}{partial} {}}} { {omega. {} {} {}}={left {frac {lambda }{mathrm {2}pi c}right)}}}{mathrm {9}{Bigl (}mathrm {362880}lambda {frac {partial varphi mathrm {}{} {m} {} {m} {} {m} {} {} {c}c} {c}c}c}c}c}c}c}c}c}ccc}ccc}ccc}ccccc}ccH00}ccH00}cH0}cccH00}cH00}ccc}}cH00}cH00}c}cH00}c}cH00}ccH00}c}cc }+mathrm {1451520} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}}+mathrm {1693440} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {}lambda mathrm {}} {cc] {cH009} {ccH002}}} {cH00}}} {cccccccH00}}}}ccccccccH00}cccccccccH00}cccccccccccH00}cH00}ccH00}ccH00}cH00cccH00}ccH00}cH00}ccH00}ccccccH004cccH. {3}}}+mathrm {846720} {lambda }{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}}+mathrm {211680} {lambda }{mathrm {5}} {frac {partial } {5}varphi mathrm { {} lambda mathrm {}} {ccH00}} {cambial {lambda. {5}}}+mathrm {28224} {lambda }{mathrm {6} {fn} {c}varphi mathrm {} lambda mathrm {}} {ccH00} {cH00} {ccH0} {cH0}} {ccH00}} {ccH009}}}} {cH00cH00}}} {cccH00}}}}} {cH00}}}}}ccccccccH00}cccccH00}ccH00}ccH00}}cH00}ccccH00}ccH00}cH00}cccH00}ccH00}ccH00}cH00}cH00}cccH00}ccH00}ccH00}cccH. {6}}}+\\+mhm} {lambda }{mathrm} {m}} {mcH0} {cH0} {cH0}}} {cH0}}}}}}}\\\\m\\\m\m\mm\\\\m\\mmm\\\mmm\\m\\mm}mcH0cH0cH0cH0cH0cH0cH0cH0cH0\\\cH0cH0cH0cH0cH0cH0cH0cH0cH0cH0cH0cH0cH0cH0\cH0cH0cH0\cH0\ {7} {fn} {fnK}varphi mathrm {} lambda mathrm {}}} {cluido {fn]} {fnuncial {lambda. {7}}}}+mathrm {72} {lambda }{mathrm {8}{frac {partial }{8}varphi mathrm {}lambda mathrm {}} {fnuncio {c]} {ccccH004cH009} {cH00}}}}} {cccccccccH00ccccccH00}cccccH00cccH00cccH00}cccccccH00}cH00ccccccH00ccH00cccH00}cH00}cH0}cH004cH004cH004cccH004ccc. {8}}}+{lambda }{mathrm {9}{frac {partial ^{mathrm} {9} } varphi mathrm { {} lambda mathrm {)} {partial {lambda. {}}} {Bigr)}end{array}}∂ ∂ 10φ φ ()⋅ ⋅ )∂ ∂ ⋅ ⋅ 10=()λ λ 2π π c)10()3628800λ λ ∂ ∂ φ φ ()λ λ )∂ ∂ λ λ +16329600λ λ 2∂ ∂ 2φ φ ()λ λ )∂ ∂ λ λ 2+21772800λ λ 3∂ ∂ 3φ φ ()λ λ )∂ ∂ λ λ 3+12700800λ λ 4∂ ∂ 4φ φ ()λ λ )∂ ∂ λ λ 4+3810240λ λ 5∂ ∂ 5φ φ ()λ λ )∂ ∂ λ λ 5+635040λ λ 6∂ ∂ 6φ φ ()λ λ )∂ ∂ λ λ 6++60480λ λ 7∂ ∂ 7φ φ ()λ λ )∂ ∂ λ λ 7+3240λ λ 8∂ ∂ 8φ φ ()λ λ )∂ ∂ λ λ 8+90λ λ 9∂ ∂ 9φ φ ()λ λ )∂ ∂ λ λ 9+λ λ 10∂ ∂ 10φ φ ()λ λ )∂ ∂ λ λ 10){displaystyle {begin{l}{frac {{partial }varphi mathrm { {}omega mathrm {}} {partial} {fnuncio}} {fnuncio} {fnuncio}} {fnuncio}}} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrom {cH} {m {2}fnMicrom {fnMicrom}}}}}}} {m} {mm} {m} {mcH00}cH00}cH00} {cH00}cH00}}}}}}}cH00} {cH00}cH00} {cH00}}cH00}}}}}}cH00}cH00}cH00} {cH00}}cH00}}}}}}}}}cH00} {cH00} {cH00}}cH00}}}cH00}}cH00}}}}}}}}}}}cH00} {cH00}}cH00}}}cH00}}}}}}} }+mathrm {16329600} {lambda }{mathrm {2} {fnMicroc {partial }{2}varphi mathrm { {} lambda mathrm {)}} {cluido {lambda. {2}}}+mathrm {21772800} {lambda }{mathrm {3}{frac {partial }{3}varphi mathrm {} {lambda mathrm {}} {c] {ccH002} {ccH009} {cH00}} {cccH00}}}}}} {cccccH00cccH00ccH00}}}}}}ccccccccccH00ccccccccH00}cH00ccH00cccH00ccH00cccH00}}cH00}cH00}}cH00cccccccH004cccH. {3}}}+mathrm {12700800} {lambda }{mathrm {4} {fnK} {4}varphi mathrm {} lambda mathrm {)} {fnuncio {fn]} {mfnuncio {cH009} {cH00}} {cH00}} {cH00}}}} {cH00}. {4}}}+mathrm {3810240} {lambda }{mathrm {5}} {frac {partial } {5}varphi mathrm { {} lambda mathrm {}} {ccH00}} {cambial {lambda. {5}}}+mathrm {635040} {lambda }{mathrm {6} {fn} {c}varphi mathrm {} lambda mathrm {}} {ccH00} {cH00} {ccH0} {cH0}} {ccH00}} {ccH009}}}} {cH00cH00}}} {cccH00}}}}} {cH00}}}}}ccccccccH00}cccccH00}ccH00}ccH00}}cH00}ccccH00}ccH00}cH00}cccH00}ccH00}ccH00}cH00}cH00}cccH00}ccH00}ccH00}cccH. {6}}}+\\+mhm {60480} {lambda }{mathrm} {7} {fn} {fnK}varphi mathrm {} lambda mathrm {}}} {cluido {fn]} {fnuncial {lambda. {7}}}+mathrm {3240} {lambda }{mathrm {8}{frac {partial }{8}varphi mathrm {} {lambda mathrm {}} {fnuncio {c]} {cccH004cH009} {cH00}}}}} {ccccccccccH00ccccccH00cccccH00cccH00}cccH00cccccccH00}cH00}cccccH00}ccH00ccccccH00}cH004cH00cH004cH004ccH004cccc. {8}}}+mathrm {90} {lambda}{mathrm {} {fnMicroc {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f}}} {fnMicroc} {fnMicrosoft} {fnMicrosoft}} {fn}} {fnMicroc {f}}} {fnMicroc {fnMicroc}}}} {f}}}}}} {f}} {\f}f}}}f}\f}}}f}f} {f} {f} {f}f}}f}f}f}f}f}f}f}f}f}fnMicrocf}f}f}\f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fn }{9}varphi mathrm { {} lambda mathrm {)}{partial {lambda. {9}}}+{lambda }{mathrm {10}{frac {partial }{10}varphi mathrm {}lambda mathrm {}} {cH00} {cH00} {cH00}} {cH00}}} {cH00}cH00}}}} {cccH00}}}}}}}}}ccccH00cccH00}cH00}cccccH00}ccH00}cccccccccccH00}ccH00}ccH00}cH00}ccccccH00}cH00}cH00}cccH00}ccH0}ccH00}cccH {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}
Dispersión espacial
En electromagnetismo y óptica, el término dispersión generalmente se refiere a la dispersión temporal o de frecuencia antes mencionada. La dispersión espacial se refiere a la respuesta no local del medio al espacio; esto se puede reformular como la dependencia del vector de onda de la permitividad. Para un medio anisotrópico ejemplar, la relación espacial entre el campo eléctrico y el campo de desplazamiento eléctrico se puede expresar como una convolución:
- Di()t,r)=Ei()t,r)+∫ ∫ 0JUEGO JUEGO ∫ ∫ fik()τ τ ;r,r.)Ek()t− − τ τ ,r.)dV.dτ τ ,{displaystyle D_{i}(t,r)=E_{i}(t,r)+int _{0}infty }int f_{ik}(tau;r,r')E_{k}(t-taur'),dV',dtau}
donde el núcleo fik{displaystyle f_{ik} es la respuesta dieléctrica (susceptibilidad); sus índices lo hacen en general un tensor para dar cuenta de la anisotropía del medio. La dispersión espacial es insignificante en la mayoría de los casos macroscópicos, donde la escala de variación Ek()t− − τ τ ,r.){displaystyle E_{k}(t-taur)} es mucho más grande que las dimensiones atómicas, porque el núcleo dieléctrico muere a distancias macroscópicas. Sin embargo, puede dar lugar a efectos macroscópicos no insignificantes, en particular en la realización de medios como metales, electrolitos y plasmas. La dispersión espacial también juega papel en la actividad óptica y la ampliación de Doppler, así como en la teoría de los metamateriales.
En gemología
| Nombre | B-G | C-F |
|---|---|---|
| Cinnabar (HgS) | 0.40 | — |
| Sintético. rutilo | 0,330 | 0.190 |
| Rutil (TiO)2) | 0,280 | 0,120–0,180 |
| Anatasa (TiO2) | 0.213–0.259 | — |
| Wulfenite | 0.203 | 0.133 |
| Vanadinite | 0.202 | — |
| Fabulite | 0.190 | 0.109 |
| Sphalerite (ZnS) | 0.156 | 0,088 |
| Sulfuro (S) | 0.155 | — |
| Stibiotantalite | 0.146 | — |
| Goethite (FeO(OH)) | 0.14 | — |
| Brookite (TiO)2) | 0.131 | 0.12 a 1,80 |
| Zincite (ZnO) | 0.127 | — |
| Linobate | 0,13 | 0,075 |
| Moissanite sintético (SiC) | 0.104 | — |
| Cassiterite (SnO)2) | 0,071 | 0,035 |
| Zirconia (ZrO)2) | 0,060 | 0,035 |
| Powellite (CaMoO4) | 0,058 | — |
| Andradite | 0,057 | — |
| Demantoid | 0,057 | 0,034 |
| Cerussite | 0,055 | 0,033–0.050 |
| Titanito | 0,051 | 0,019–0,038 |
| Benitorito | 0,046 | 0,026 |
| Anglesita | 0,044 | 0,025 |
| Diamantes (C) | 0,044 | 0,025 |
| Cristal Flint | 0,041 | — |
| Hyacinth | 0,039 | — |
| Jargoon | 0,039 | — |
| Starlite | 0,039 | — |
| Zircon (ZrSiO4) | 0,039 | 0,022 |
| GG | 0,038 | 0,022 |
| Scheelite | 0,038 | 0,026 |
| Dioptase | 0,036 | 0,021 |
| Whe Vinay wellite | 0,034 | — |
| Alabaster | 0,033 | — |
| Gypsum | 0,033 | 0,008 |
| Epidodio | 0,03 | 0,012–0,027 |
| Acroite | 0,017 | — |
| Cordierita | 0,017 | 0,009 |
| Danburite | 0,017 | 0,009 |
| Dravite | 0,017 | — |
| Elbaite | 0,017 | — |
| Herderite | 0,017 | 0,008–0.009 |
| Oculto | 0,017 | 0,010 |
| Indicolite | 0,017 | — |
| Liddicoatite | 0,017 | — |
| Kunzite | 0,017 | 0,010 |
| Rubellite | 0,017 | 0,008–0.009 |
| Schorl | 0,017 | — |
| Scapolite | 0,017 | — |
| Spodumene | 0,017 | 0,010 |
| Tourmaline | 0,017 | 0,009–0.011 |
| Verdelite | 0,017 | — |
| Andalusita | 0,016 | 0,009 |
| Baryte (BaSO)4) | 0,016 | 0,009 |
| Euclase | 0,016 | 0,009 |
| Alexandrite | 0,015 | 0,011 |
| Chrysoberyl | 0,015 | 0,011 |
| Hambergite | 0,015 | 0,009–0.010 |
| Phenakite | 0,01 | 0,009 |
| Rhodochrosite | 0,015 | 0,010–0,020 |
| Sillimanite | 0,015 | 0,009–0.012 |
| Smithsonite | 0,014–0.031 | 0,008–0.017 |
| Amblygonite | 0,014–0,015 | 0,008 |
| Aquamarine | 0,014 | 0,009–0.013 |
| Beryl | 0,014 | 0,009–0.013 |
| Brasilita | 0,014 | 0,008 |
| Celestine | 0,014 | 0,008 |
| Goshenite | 0,014 | — |
| Heliodor | 0,014 | 0,009–0.013 |
| Morganite | 0,014 | 0,009–0.013 |
| Pyroxmangite | 0,015 | — |
| Sinth. esqueelite | 0,015 | — |
| Dolomite | 0,013 | — |
| Magnesita (MgCO)3) | 0,012 | — |
| Sinth. Esmeralda | 0,012 | — |
| Sinth. alexandrite | 0,011 | — |
| Sinth. sapphire (Al2O3) | 0,011 | — |
| fosfofilita | 0,010–0.011 | — |
| Enstatite | 0,010 | — |
| Anorthite | 0,009–0.010 | — |
| Actinolite | 0,009 | — |
| Jeremejevite | 0,009 | — |
| Nepheline | 0,008–0.009 | — |
| Apophyllite | 0,008 | — |
| Hauyne | 0,008 | — |
| Natrolite | 0,008 | — |
| Sinth. quartz (SiO2) | 0,008 | — |
| Aragonita | 0,007–0.012 | — |
| Augelite | 0,007 | — |
| Tanzanita | 0,030 | 0,011 |
| Thulite | 0,03 | 0,011 |
| Zoisite | 0,03 | — |
| YAG | 0,028 | 0,015 |
| Almandine | 0,027 | 0,013–016 |
| Hessonite | 0,027 | 0,013–0,015 |
| Spessartine | 0,027 | 0,015 |
| Uvarovite | 0,027 | 0,014–0.021 |
| Willemite | 0,027 | — |
| Pleonaste | 0,026 | — |
| Rhodolite | 0,026 | — |
| Boracite | 0,024 | 0,012 |
| Cryolite | 0,024 | — |
| Staurolite | 0,023 | 0,012–0,013 |
| Pyrope | 0,022 | 0,013–016 |
| Diaspore | 0,02 | — |
| Grossular | 0,020 | 0,012 |
| Hemimorfita | 0,020 | 0,013 |
| Kyanite | 0,020 | 0,011 |
| Peridot | 0,020 | 0,012–0,013 |
| Spinel | 0,020 | 0,011 |
| Vesuvianite | 0,019–0,025 | 0,014 |
| Clinozoisita | 0,019 | 0,011–0,014 |
| Labradorite | 0,019 | 0,010 |
| Axinite | 0,018–0,020 | 0,011 |
| Ekanite | 0,018 | 0,012 |
| Kornerupine | 0,018 | 0,010 |
| Corundum (Al2O3) | 0,018 | 0,011 |
| Rhodizite | 0,018 | — |
| Ruby (Al2O3) | 0,018 | 0,011 |
| zafiro (Al2O3) | 0,018 | 0,011 |
| Sinhalite | 0,018 | 0,010 |
| Sodalite | 0,018 | 0,009 |
| Sinth. corundum | 0,018 | 0,011 |
| Diopside | 0,018–0,020 | 0,01 |
| Esmeralda | 0,014 | 0,009–0.013 |
| Topacio | 0,014 | 0,008 |
| Amatista (SiO2) | 0,013 | 0,008 |
| Anhydrite | 0,013 | — |
| Apatite | 0,013 | 0,010 |
| Apatite | 0,013 | 0,008 |
| Aventurine | 0,013 | 0,008 |
| Citrine | 0,013 | 0,008 |
| Morion | 0,013 | — |
| Prasiolite | 0,013 | 0,008 |
| Quartz (SiO2) | 0,013 | 0,008 |
| Cuarzo ahumado (SiO2) | 0,013 | 0,008 |
| Cuarzo de rosa (SiO2) | 0,013 | 0,008 |
| Albite | 0,012 | — |
| Bytownite | 0,012 | — |
| Feldspar | 0,012 | 0,008 |
| Moonstone | 0,012 | 0,008 |
| Orthoclase | 0,012 | 0,008 |
| Pollucite | 0,012 | 0,007 |
| Sanidine | 0,012 | — |
| Sunstone | 0,012 | — |
| Beryllonite | 0,010 | 0,007 |
| Cancrinita | 0,010 | 0,008–0.009 |
| Leucite | 0,010 | 0,008 |
| Obsidian | 0,010 | — |
| Strontianite | 0,008–0,028 | — |
| Calcite (CaCO)3) | 0,008–0.017 | 0,013–0,014 |
| Fluorita (CaF)2) | 0,007 | 0,004 |
| Hematite | 0,50 | — |
| Tarea sintética (SnO2) | 0,041 | — |
| Gahnite | 0,019–0.021 | — |
| Datolite | 0,016 | — |
| Tremolite | 0,006–0.007 | — |
En la terminología técnica de la gemología, dispersión es la diferencia en el índice de refracción de un material en B y G (686,7 nm y 430,8 nm) o C y F (656,3 nm y 486,1 nm) longitudes de onda de Fraunhofer, y pretende expresar el grado en que un prisma cortado de la piedra preciosa demuestra "fuego". Fuego es un término coloquial utilizado por los gemólogos para describir la naturaleza dispersiva de una piedra preciosa o la falta de ella. La dispersión es una propiedad material. La cantidad de fuego demostrada por una piedra preciosa dada es una función de los ángulos de las facetas de la piedra preciosa, la calidad del pulido, el entorno de iluminación, el índice de refracción del material, la saturación del color y la orientación del observador. en relación con la piedra preciosa.
En imágenes
En los objetivos fotográficos y microscópicos, la dispersión provoca una aberración cromática, lo que provoca que los diferentes colores de la imagen no se superpongan correctamente. Se han desarrollado diversas técnicas para contrarrestar esto, como el uso de acromáticos, lentes multielementos con vidrios de diferente dispersión. Están construidos de tal manera que las aberraciones cromáticas de las diferentes partes se anulan.
Emisiones de pulsar
Los púlsares son estrellas de neutrones giratorias que emiten pulsos a intervalos muy regulares que van desde milisegundos hasta segundos. Los astrónomos creen que los pulsos se emiten simultáneamente en una amplia gama de frecuencias. Sin embargo, como se observa en la Tierra, los componentes de cada pulso emitido en frecuencias de radio más altas llegan antes que los emitidos en frecuencias más bajas. Esta dispersión ocurre debido al componente ionizado del medio interestelar, principalmente los electrones libres, que hacen que la velocidad del grupo sea dependiente de la frecuencia. El retraso adicional agregado a una frecuencia ν es
- t=kDM⋅ ⋅ ()DM.. 2),{displaystyle t=k_{text{DM}cdot left({frac {text{DM}{nu ^{2}}}right),}
donde la constante de dispersión kDM viene dada por
- kDM=e22π π mec.. 4.149GHz2pc− − 1cm3ms,{displaystyle k_{text{DM}={frac} {2}{2}{2pi. 4.149~{text{GHz}} {2},{text{pc}}{-1},{text{cm}}} {3},{text{ms}}}
y la medida de dispersión (DM) es la densidad de columna de electrones libres (contenido total de electrones), es decir, la densidad numérica de electrones ne integrada a lo largo de la trayectoria recorrida por el fotón desde el púlsar hasta la Tierra, y está dada por
- DM=∫ ∫ 0dnedl{displaystyle {text{DM}=int ¿Qué?
con unidades de parsecs por centímetro cúbico (1 pc/cm3 = 30,857×1021 m−2).
Normalmente para las observaciones astronómicas, este retraso no se puede medir directamente, ya que se desconoce el tiempo de emisión. Lo que puede medirse es la diferencia en los tiempos de llegada en dos frecuencias diferentes. El retraso Δt entre un νhi de alta frecuencia y un El componente νlo de baja frecuencia de un pulso será
- Δ Δ t=kDM⋅ ⋅ DM⋅ ⋅ ()1.. Lo sé.2− − 1.. Hola.2).{displaystyle Delta t=k_{text{DM}cdot {text{DM}cdot left({frac {1}{nu} ¿Qué? {1}{nu _{hi} {2}}derecha).}
Reescribir la ecuación anterior en términos de Δt permite determinar la DM midiendo los tiempos de llegada del pulso en múltiples frecuencias. Esto, a su vez, se puede utilizar para estudiar el medio interestelar, así como para permitir que se combinen las observaciones de púlsares en diferentes frecuencias.
Contenido relacionado
Caleidoscopio
Hipótesis del impacto gigante
Efecto auditivo de microondas