Dispersión dinámica de la luz

La dispersión dinámica de la luz (DLS) es una técnica de física que se puede utilizar para determinar el perfil de distribución de tamaño de partículas pequeñas en suspensión o polímeros en solución. En el ámbito de la DLS, las fluctuaciones temporales se analizan habitualmente utilizando la función de autocorrelación de intensidad o fotón (también conocida como espectroscopia de correlación de fotones – PCS o dispersión de luz cuasielástica – QELS). En el análisis del dominio del tiempo, la función de autocorrelación (ACF) normalmente decae a partir de un tiempo de retardo cero, y una dinámica más rápida debido a partículas más pequeñas conduce a una decorrelación más rápida de la traza de intensidad dispersa. Se ha demostrado que la ACF de intensidad es la transformada de Fourier del espectro de potencia y, por lo tanto, las mediciones DLS se pueden realizar igualmente bien en el dominio espectral. La DLS también se puede utilizar para investigar el comportamiento de fluidos complejos, como soluciones poliméricas concentradas.

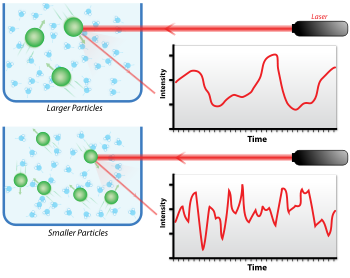
Se dispara una fuente de luz monocromática, normalmente un láser, a través de un polarizador hacia una muestra. La luz dispersada pasa luego por un segundo polarizador, donde es recogida por un fotomultiplicador y la imagen resultante se proyecta en una pantalla. Esto se conoce como patrón de moteado (Figura 1).

Todas las moléculas de la solución reciben la luz y todas ellas difractan la luz en todas las direcciones. La luz difractada de todas las moléculas puede interferir de forma constructiva (regiones claras) o destructiva (regiones oscuras). Este proceso se repite a intervalos cortos de tiempo y el conjunto de patrones de motas resultante se analiza mediante un autocorrelacionador que compara la intensidad de la luz en cada punto a lo largo del tiempo. Los polarizadores se pueden configurar en dos configuraciones geométricas. Una es una geometría vertical/vertical (VV), donde el segundo polarizador permite el paso de la luz que va en la misma dirección que el polarizador principal. En la geometría vertical/horizontal (VH), el segundo polarizador permite el paso de la luz que no va en la misma dirección que la luz incidente.

Cuando la luz incide sobre partículas pequeñas, se dispersa en todas direcciones (dispersión de Rayleigh) siempre que las partículas sean pequeñas en comparación con la longitud de onda (por debajo de los 250 nm). Incluso si la fuente de luz es un láser y, por lo tanto, es monocromática y coherente, la intensidad de la dispersión fluctúa con el tiempo. Esta fluctuación se debe a que las partículas pequeñas en suspensión experimentan un movimiento browniano, por lo que la distancia entre los dispersores en la solución cambia constantemente con el tiempo. Esta luz dispersa sufre entonces una interferencia constructiva o destructiva por parte de las partículas circundantes y, dentro de esta fluctuación de intensidad, se contiene información sobre la escala de tiempo del movimiento de los dispersores. La preparación de la muestra, ya sea por filtración o centrifugación, es fundamental para eliminar el polvo y los artefactos de la solución.

La información dinámica de las partículas se deriva de la autocorrelación del trazo de intensidad registrado durante el experimento. La curva de autocorrelación de segundo orden se genera a partir del trazo de intensidad de la siguiente manera:

${\displaystyle g^{2}(q;\tau)={\frac {\langle I(t)I(t+\tau)\rangle }{\langle I(t)\rangle ^{2}}}}}$

Donde g²()q;τ) es la función de autocorrelación en un vector de onda particular, q, y tiempo de demora, τ, y I es la intensidad. Los soportes angulares ${\displaystyle \langle \cdot \rangle }$ denota el operador de valor esperado, que en algunos textos es denotado por un capital E.

En los intervalos de tiempo cortos, la correlación es alta porque las partículas no tienen la posibilidad de moverse en gran medida desde el estado inicial en el que se encontraban. Por lo tanto, las dos señales permanecen esencialmente inalteradas cuando se comparan después de un intervalo de tiempo muy corto. A medida que los intervalos de tiempo se hacen más largos, la correlación decae exponencialmente, lo que significa que, después de que haya transcurrido un largo período, no hay correlación entre la intensidad dispersa de los estados inicial y final. Este decaimiento exponencial está relacionado con el movimiento de las partículas, específicamente con el coeficiente de difusión. Para ajustar el decaimiento (es decir, la función de autocorrelación), se utilizan métodos numéricos, basados en cálculos de distribuciones supuestas. Si la muestra es monodispersa (uniforme), entonces el decaimiento es simplemente un exponencial único. La ecuación de Siegert relaciona la función de autocorrelación de segundo orden con la función de autocorrelación de primer orden g¹(q;τ) de la siguiente manera:

${\displaystyle g^{2}(q;\tau)=1+\beta \left[g^{1}(q;\tau)\right]^{2}$

donde el primer término de la suma está relacionado con el valor de referencia (≈1) y el parámetro β es un factor de corrección que depende de la geometría y la alineación del haz láser en la configuración de dispersión de luz. Es aproximadamente igual al inverso del número de motas (ver Patrón de motas) de las que se recoge la luz. Un foco más pequeño del haz láser produce un patrón de motas más grueso, una menor cantidad de motas en el detector y, por lo tanto, una autocorrelación de segundo orden mayor. El uso más importante de la función de autocorrelación es su uso para la determinación del tamaño.

La dispersión de luz dinámica permite conocer las propiedades dinámicas de los materiales blandos midiendo eventos de dispersión individuales, lo que significa que cada fotón detectado ha sido dispersado por la muestra exactamente una vez. En principio, las mediciones DLS se pueden realizar con el detector colocado en cualquier ángulo. La elección del mejor ángulo depende de las propiedades de la muestra, como la turbidez y el tamaño de las partículas. La detección por dispersión posterior (por ejemplo, 173° o 175°) es particularmente interesante para muestras turbias y altamente concentradas, que contienen partículas grandes. La detección por dispersión lateral (90°) se recomienda para muestras con dispersión débil, incluidas partículas pequeñas y muestras transparentes. Finalmente, la detección por dispersión frontal (por ejemplo, 13° o 15°) es adecuada para la detección de muestras que contienen partículas pequeñas con pocas partículas grandes. Algunos instrumentos DLS en el mercado también permiten la selección automática del ángulo en función de una medición de transmitancia continua.

En el extremo inferior del rango de turbidez, el método de espectroscopia de dispersión amplificada por cavidad utiliza una cavidad integradora para alargar las trayectorias de los fotones a través de muestras casi sin dispersión. A diferencia de los instrumentos DLS convencionales, este método es independiente del ángulo, ya que sondea las muestras de forma isótropa desde todas las direcciones.

Aunque la medición DLS mediante detección de un solo ángulo ha sido la técnica más difundida, su aplicación en muchos sistemas de relevancia científica e industrial ha sido limitada debido a la dispersión múltiple, que se da con frecuencia, en la que los fotones se dispersan varias veces por la muestra antes de ser detectados. La interpretación precisa se vuelve extremadamente difícil para sistemas con contribuciones no despreciables de la dispersión múltiple. Especialmente para partículas más grandes y aquellas con un alto contraste de índice de refracción, esto limita la técnica a concentraciones de partículas muy bajas y, por lo tanto, una gran variedad de sistemas quedan excluidos de las investigaciones con dispersión de luz dinámica. Sin embargo, como lo demostró Schaetzel, es posible suprimir la dispersión múltiple en experimentos de dispersión de luz dinámica mediante un enfoque de correlación cruzada. La idea general es aislar la luz dispersada individualmente y suprimir las contribuciones no deseadas de la dispersión múltiple en un experimento de dispersión de luz dinámica. Se han desarrollado y aplicado diferentes implementaciones de dispersión de luz por correlación cruzada. Actualmente, el método más utilizado es el denominado método de dispersión de luz dinámica tridimensional. El mismo método también se puede utilizar para corregir los datos de dispersión de luz estática en función de las contribuciones de dispersión múltiple. Alternativamente, en el límite de una fuerte dispersión múltiple, se puede aplicar una variante de dispersión de luz dinámica denominada espectroscopia de ondas difusas.

Una vez generados los datos de autocorrelación, se pueden emplear diferentes enfoques matemáticos para obtener "información" a partir de ellos. El análisis de la dispersión se facilita cuando las partículas no interactúan a través de colisiones o fuerzas electrostáticas entre iones. Las colisiones entre partículas se pueden suprimir mediante dilución y los efectos de carga se reducen mediante el uso de sales para colapsar la doble capa eléctrica.

El enfoque más simple es tratar la función de autocorrelación de primer orden como una desintegración exponencial simple. Esto es apropiado para una población monodispersa.

${\displaystyle \ g^{1}(q;\tau)=\exp(-\Gamma \tau)\,}$

donde Γ es la tasa de decaimiento. El coeficiente de difusión traslacional D_t puede derivarse en un solo ángulo o en un rango de ángulos dependiendo del vector de onda q.

${\displaystyle \\Gamma =q^{2}D_{t}\,}$

con

${\displaystyle \ q={\frac {4\pi {\fnMicroc {\theta }}\sin\left {\fnMicroc {\theta }}\right)}}$

donde λ es la longitud de onda del láser incidente, n₀ es el índice de refracción del solvente y θ es el ángulo en el que se encuentra el detector con respecto a la celda de muestra.

El índice de refracción del disolvente desempeña un papel crucial en la dispersión de la luz y es importante para calcular el radio de Stokes a partir de la ecuación de Stokes-Einstein. Por lo tanto, los datos previos del índice de refracción del medio de dispersión deben evaluarse con instrumentos especializados, conocidos como refractómetros. Alternativamente, los instrumentos DLS que contienen un módulo de medición del índice de refracción permiten una buena estimación de este importante parámetro dentro de ±0,5 %, que es la precisión definida por la norma ISO 22412:2017 para los valores del índice de refracción requeridos para DLS. Además del índice de refracción del medio, el índice de refracción de las partículas solo es necesario cuando se analizan partículas de mayor tamaño (normalmente superiores a 100 nm) y se necesitan distribuciones de tamaño ponderadas por volumen o número. En estos casos, se requiere un conocimiento previo del índice de refracción y la absorbancia del material para aplicar la dispersión de Mie.

Dependiendo de la anisotropía y polidispersidad del sistema, el gráfico resultante de (Γ/q²) vs. q² puede o no mostrar una dependencia angular. Las partículas esféricas pequeñas no mostrarán dependencia angular, por lo tanto no habrá anisotropía. Un gráfico de (Γ/q²) vs. q² dará como resultado una línea horizontal. Las partículas con una forma distinta a la esférica mostrarán anisotropía y, por lo tanto, una dependencia angular al representar gráficamente (Γ/q²) frente a q². La intersección será en cualquier caso el D_t. Por lo tanto, existe un ángulo de detección óptimo θ para cada tamaño de partícula. Siempre se debe realizar un análisis de alta calidad en varios ángulos de dispersión (DLS multiángulo). Esto se vuelve aún más importante en una muestra polidispersa con una distribución de tamaño de partícula desconocida. En ciertos ángulos, la intensidad de dispersión de algunas partículas abrumará por completo la débil señal de dispersión de otras partículas, haciéndolas invisibles para el análisis de datos en este ángulo. Los instrumentos DLS que solo funcionan en un ángulo fijo solo pueden ofrecer buenos resultados para algunas partículas. Por lo tanto, la precisión indicada de un instrumento DLS con un solo ángulo de detección solo es válida para ciertas partículas.

D_t se utiliza a menudo para calcular el radio hidrodinámico de una esfera a través de la ecuación de Stokes-Einstein. Es importante tener en cuenta que el tamaño determinado por la dispersión de luz dinámica es el tamaño de una esfera que se mueve de la misma manera que el dispersor. Por lo tanto, por ejemplo, si el dispersor es un polímero de bobina aleatoria, el tamaño determinado no es el mismo que el radio de giro determinado por la dispersión de luz estática. También es útil señalar que el tamaño obtenido incluirá cualquier otra molécula o moléculas de disolvente que se muevan con la partícula. Por lo tanto, por ejemplo, el oro coloidal con una capa de surfactante aparecerá más grande por dispersión de luz dinámica (que incluye la capa de surfactante) que por microscopía electrónica de transmisión (que no "ve" la capa debido al bajo contraste).

En la mayoría de los casos, las muestras son polidispersas. Por lo tanto, la función de autocorrelación es una suma de las desintegraciones exponenciales correspondientes a cada una de las especies de la población.

${\displaystyle g^{1}(q\tau)=\sum ¿Por qué?$

Resulta tentador obtener datos para g¹(q;τ) e intentar invertir lo anterior para extraer G(Γ). Dado que G(Γ) es proporcional a la dispersión relativa de cada especie, contiene información sobre la distribución de tamaños. Sin embargo, esto se conoce como un problema mal planteado. Los métodos descritos a continuación (y otros) se han desarrollado para extraer la mayor cantidad posible de información útil de una función de autocorrelación.

Uno de los métodos más comunes es el método cumulante, del cual además de la suma de las exponenciales anteriores, se puede derivar más información sobre la varianza del sistema de la siguiente manera:

${\displaystyle \ g^{1}(q\tau)=\exp \left(-{\bar) {\fnMicrosoft Sans Serif}\left(\tau) - {\frac # - ¿Qué? ¿Qué?$

donde Γ es la tasa de decaimiento promedio y μ₂/Γ² es el índice de polidispersidad de segundo orden (o una indicación de la varianza). También se puede derivar un índice de polidispersidad de tercer orden, pero esto es necesario solo si las partículas del sistema son altamente polidispersas. El coeficiente de difusión traslacional promediado en z D_z se puede derivar en un solo ángulo o en un rango de ángulos dependiendo del vector de onda q.

${\displaystyle\ {\bar {\\\\\\\\\\\\\\\\\fnMicrosoft\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\f\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ ¿Qué?$

Uno debe notar que el método acumulativo es válido para pequeños τ y suficientemente estrechos G().). Uno debe usar rara vez parámetros más allá de μ₃, ya que la superación de datos con muchos parámetros en una expansión de la serie de energía hará que todos los parámetros, incluyendo ${\displaystyle \scriptstyle {\bar {\Gamma }$ y μ₂menos preciso. El método acumulativo es mucho menos afectado por el ruido experimental que los métodos siguientes.

La distribución del tamaño de las partículas también se puede obtener utilizando la función de autocorrelación. Sin embargo, las muestras polidispersas no se resuelven bien mediante el análisis de ajuste acumulativo. Por lo tanto, la combinación de algoritmos de mínimos cuadrados no negativos (NNLS) con métodos de regularización, como la regularización de Tikhonov, se puede utilizar para resolver muestras multimodales. Una característica importante de la optimización NNLS es el término de regularización utilizado para identificar soluciones específicas y minimizar la desviación entre los datos de medición y el ajuste. No existe un término de regularización ideal que sea adecuado para todas las muestras. La forma de este término puede determinar si la solución representará una distribución amplia general con un pequeño número de picos o si se ajustarán poblaciones estrechas y discretas. Alternativamente, el cálculo de la distribución del tamaño de las partículas se realiza utilizando el algoritmo CONTIN.

Se puede lograr un método alternativo para analizar la función de autocorrelación a través de una transformada de Laplace inversa conocida como CONTIN, desarrollada por Steven Provencher. El análisis CONTIN es ideal para sistemas heterodispersos, polidispersos y multimodales que no se pueden resolver con el método cumulante. La resolución para separar dos poblaciones de partículas diferentes es aproximadamente un factor de cinco o superior y la diferencia en intensidades relativas entre dos poblaciones diferentes debe ser menor que 1:10⁻⁵.

El método de máxima entropía es un método de análisis que tiene un gran potencial de desarrollo. El método también se utiliza para la cuantificación de los datos de velocidad de sedimentación a partir de la ultracentrifugación analítica. El método de máxima entropía implica varios pasos iterativos para minimizar la desviación de los datos ajustados respecto de los datos experimentales y, posteriormente, reducir el χ² de los datos ajustados.

Si la partícula en cuestión no es esférica, también debe considerarse el movimiento rotacional, ya que la dispersión de la luz será diferente según la orientación. Según Pecora, el movimiento browniano rotacional afectará la dispersión cuando una partícula cumpla dos condiciones: debe ser anisotrópica tanto óptica como geométricamente. Las moléculas con forma de bastón cumplen estos requisitos, por lo que debe considerarse un coeficiente de difusión rotacional además de un coeficiente de difusión traslacional. En su forma más sucinta, la ecuación aparece como

${\displaystyle {\frac {\fnK}={\frac} {5}{4}{\frac {4\mathrm {M} _{p}+2\mathrm {N} \mathrm {M} _{l}\mathrm {M} _{p}+\mathrm {M} {\fn} {\fnMicrosoft} {\fnMicrosoft}} {\fnMicrosoft}} {\fn}} {\fnMicrosoft}} {\fnMicrosoft}}} {\fnK}}}}}}} {\fnK}}}}} {\m}}}}}} {\m}}}}}} {\m}}}}} {\m}}}}}}} {\m} {\m} {\m}}}} {\m} {\m}}} {\m} {\m} {\m}}}}} {\m}}}}}}}}}}}}}} {\m}} {\m} {\m} {\m} {\m} {\m}} {\m} {\m}}}m}m}}}}}}}} {\m}} {\m} {\m}}}}}}}}} {\m}}}} {\m}}} {M} _{p}-\mathrm {N} +\mathrm {M} {l}}}$

Donde A/B es la relación de los dos modos de relajación (traslacional y rotacional), M_p contiene información sobre el eje perpendicular al eje central de la partícula, y M_l contiene información sobre el eje paralelo al eje central.

En 2007, Peter R. Lang y su equipo decidieron utilizar la dispersión dinámica de la luz para determinar la longitud de las partículas y la relación de aspecto de nanobarras de oro cortas. Eligieron este método porque no destruye la muestra y tiene una configuración relativamente sencilla. Se observaron ambos estados de relajación en la geometría VV y se utilizaron los coeficientes de difusión de ambos movimientos para calcular las relaciones de aspecto de las nanopartículas de oro.

El DLS se utiliza para caracterizar el tamaño de diversas partículas, incluidas proteínas, polímeros, micelas, jaulas de proteínas y partículas similares a virus, vesículas, carbohidratos, nanopartículas, células biológicas y geles. Si el sistema no tiene un tamaño disperso, se puede determinar el diámetro efectivo medio de las partículas. Esta medición depende del tamaño del núcleo de la partícula, el tamaño de las estructuras de la superficie, la concentración de partículas y el tipo de iones en el medio.

Dado que el DLS mide esencialmente las fluctuaciones en la intensidad de la luz dispersada debido a la difusión de partículas, se puede determinar el coeficiente de difusión de las partículas. El software DLS de los instrumentos comerciales normalmente muestra la población de partículas en diferentes diámetros. Si el sistema es monodisperso, solo debería haber una población, mientras que un sistema polidisperso mostraría múltiples poblaciones de partículas. Si hay más de una población de tamaño presente en una muestra, entonces se debe aplicar el análisis CONTIN para los instrumentos de espectroscopia de correlación de fotones, o se debe aplicar el método del espectro de potencia para los instrumentos de desplazamiento Doppler.

Los estudios de estabilidad se pueden realizar de forma cómoda mediante DLS. Las mediciones periódicas de DLS de una muestra pueden mostrar si las partículas se agregan con el tiempo al observar si el radio hidrodinámico de la partícula aumenta. Si las partículas se agregan, habrá una población mayor de partículas con un radio mayor. En algunas máquinas DLS, la estabilidad en función de la temperatura se puede analizar controlando la temperatura in situ.

• DLS determinar el radio de pequeñas cuentas en movimiento marroniano en una solución
• Dotación de partículas utilizando DLS
• Escalada dinámica de luz para la caracterización del tamaño de partículas de proteínas, polímeros y dispersiones coloidales
• Comprensión de la luz dinámica, tecnología Wyatt