Dispersión de Mie

La solución de Mie a las ecuaciones de Maxwell (también conocida como la solución de Lorenz–Mie, la solución de Lorenz–Mie–Debye o dispersión de Mie) describe la dispersión de una onda electromagnética plana por una esfera homogénea. La solución toma la forma de una serie infinita de ondas parciales multipolares esféricas. Lleva el nombre de Gustav Mie.

El término solución de Mie también se usa para las soluciones de las ecuaciones de Maxwell para la dispersión por esferas estratificadas o por cilindros infinitos, u otras geometrías en las que se pueden escribir ecuaciones separadas para las ecuaciones radial y angular. dependencia de las soluciones. El término teoría de Mie se utiliza a veces para este conjunto de soluciones y métodos; no se refiere a una teoría o ley física independiente. En términos más generales, la "dispersión de Mie" Las fórmulas son más útiles en situaciones en las que el tamaño de las partículas dispersas es comparable a la longitud de onda de la luz, en lugar de mucho más pequeño o mucho más grande.

La dispersión de Mie (a veces denominada dispersión no molecular o dispersión de partículas de aerosol) tiene lugar en los 4500 m inferiores (15 000 ft) de la atmósfera, donde pueden estar presentes muchas partículas esencialmente esféricas con diámetros aproximadamente iguales a la longitud de onda del rayo incidente. La teoría de dispersión de Mie no tiene limitación de tamaño superior y converge al límite de la óptica geométrica para partículas grandes.

Introducción

Una formulación moderna de la solución de Mie para el problema de dispersión en una esfera se puede encontrar en muchos libros, por ejemplo, Teoría electromagnética de J. A. Stratton. En esta formulación, la onda plana incidente, así como el campo de dispersión, se expande en armónicos esféricos vectoriales esféricos radiantes. El campo interno se expande en armónicos esféricos vectoriales regulares. Al hacer cumplir la condición de contorno en la superficie esférica, se pueden calcular los coeficientes de expansión del campo disperso.

Para partículas mucho más grandes o mucho más pequeñas que la longitud de onda de la luz dispersada, existen aproximaciones simples y precisas que son suficientes para describir el comportamiento del sistema. Pero para objetos cuyo tamaño está dentro de unos pocos órdenes de magnitud de la longitud de onda, por ejemplo, gotas de agua en la atmósfera, partículas de látex en pintura, gotas en emulsiones, incluida la leche, y células biológicas y componentes celulares, se necesita un enfoque más detallado.

La solución de Mie lleva el nombre de su desarrollador, el físico alemán Gustav Mie. El físico danés Ludvig Lorenz y otros desarrollaron de forma independiente la teoría de la dispersión de ondas planas electromagnéticas por una esfera dieléctrica.

El formalismo permite el cálculo de los campos eléctricos y magnéticos dentro y fuera de un objeto esférico y generalmente se usa para calcular cuánta luz se dispersa (la sección transversal óptica total) o hacia dónde va (el factor de forma). Las características notables de estos resultados son las resonancias de Mie, tamaños que se dispersan de manera particularmente fuerte o débil. Esto contrasta con la dispersión de Rayleigh para partículas pequeñas y la dispersión de Rayleigh-Gans-Debye (después de Lord Rayleigh, Richard Gans y Peter Debye) para partículas grandes. La existencia de resonancias y otras características de la dispersión de Mie la convierte en un formalismo particularmente útil cuando se usa luz dispersa para medir el tamaño de las partículas.

Aproximaciones

Aproximación de Rayleigh (dispersión)

La dispersión de Rayleigh describe la dispersión elástica de la luz por esferas que son mucho más pequeñas que la longitud de onda de la luz. La intensidad I de la radiación dispersada viene dada por

I=I0()1+#2⁡ ⁡ Silencio Silencio 2R2)()2π π λ λ )4()n2− − 1n2+2)2()d2)6,{displaystyle I=I_{0}left({frac {1+cos ^{2}theta {fnMicrosoft Sans Serif} {fnMicroc {2pi}{lambda ¿Qué?

donde I₀ es la intensidad de la luz antes de la interacción con la partícula, R es la distancia entre la partícula y el observador, θ es el ángulo de dispersión, λ es la longitud de onda de la luz considerada, n es el índice de refracción de la partícula y d es el diámetro de la partícula.

Se puede ver a partir de la ecuación anterior que la dispersión de Rayleigh depende en gran medida del tamaño de la partícula y las longitudes de onda. La intensidad de la radiación dispersada de Rayleigh aumenta rápidamente a medida que aumenta la relación entre el tamaño de las partículas y la longitud de onda. Además, la intensidad de la radiación dispersa de Rayleigh es idéntica en las direcciones directa e inversa.

El modelo de dispersión de Rayleigh falla cuando el tamaño de las partículas supera el 10 % de la longitud de onda de la radiación incidente. En el caso de partículas con dimensiones mayores que esta, se puede utilizar el modelo de dispersión de Mie para encontrar la intensidad de la radiación dispersada. La intensidad de la radiación dispersa de Mie viene dada por la suma de una serie infinita de términos y no por una simple expresión matemática. Sin embargo, se puede demostrar que la dispersión en este rango de tamaños de partículas difiere de la dispersión de Rayleigh en varios aspectos: es aproximadamente independiente de la longitud de onda y es mayor en la dirección directa que en la inversa. Cuanto mayor es el tamaño de las partículas, más luz se dispersa en la dirección de avance.

El color azul del cielo resulta de la dispersión de Rayleigh, ya que el tamaño de las partículas de gas en la atmósfera es mucho menor que la longitud de onda de la luz visible. La dispersión de Rayleigh es mucho mayor para la luz azul que para otros colores debido a su longitud de onda más corta. A medida que la luz solar atraviesa la atmósfera, su componente azul es Rayleigh fuertemente dispersado por los gases atmosféricos, pero los componentes de longitud de onda más larga (por ejemplo, rojo/amarillo) no lo son. Por lo tanto, la luz solar que llega directamente del Sol parece ser ligeramente amarilla, mientras que la luz dispersada por el resto del cielo parece azul. Durante los amaneceres y atardeceres, el efecto de la dispersión de Rayleigh en el espectro de la luz transmitida es mucho mayor debido a la mayor distancia que tienen que recorrer los rayos de luz a través del aire de alta densidad cerca de la superficie terrestre.

Por el contrario, las gotas de agua que forman las nubes tienen un tamaño comparable a las longitudes de onda de la luz visible, y la dispersión la describe el modelo de Mie en lugar del de Rayleigh. Aquí, todas las longitudes de onda de la luz visible se dispersan de manera aproximadamente idéntica y, por lo tanto, las nubes parecen ser blancas o grises.

Aproximación de Rayleigh-Gans

La aproximación de Rayleigh-Gans es una solución aproximada a la dispersión de la luz cuando el índice de refracción relativo de la partícula es cercano al del entorno y su tamaño es mucho más pequeño en comparación con la longitud de onda de la luz dividida por | n − 1|, donde n es el índice de refracción:

Silencion− − 1Silencio≪ ≪ 1kdSilencion− − 1Silencio≪ ≪ 1{fnMicrosoftware {fnMicrosoft} {fnMicrosoft}}

Donde k{textstyle k} es el portador de onda de la luz (k=2π π λ λ {fnMicroc {2fnMicroc} ♫{lambda }), y d{displaystyle d} se refiere a la dimensión lineal de la partícula. La condición anterior se conoce a menudo como ópticamente suave y la aproximación sostiene para partículas de forma arbitraria.

Aproximación de difracción anómala de van de Hulst

La aproximación de difracción anómala es válida para esferas grandes (en comparación con la longitud de onda) y ópticamente blandas; suave en el contexto de la óptica implica que el índice de refracción de la partícula (m) difiere solo ligeramente del índice de refracción del entorno, y la partícula somete a la onda a un pequeño cambio de fase. La eficiencia de extinción en esta aproximación viene dada por

Q=2− − 4ppecado⁡ ⁡ p+4p2()1− − #⁡ ⁡ p),{displaystyle Q=2-{frac {4} {p}sin p+{frac {4} {4}} {1-cos p),}

donde Q es el factor de eficiencia de la dispersión, que se define como la relación entre la sección transversal de dispersión y la sección transversal geométrica πa².

El término p = 4πa(n − 1)/λ tiene como significado físico el retraso de fase de la onda que pasa por el centro de la esfera, donde a es el radio de la esfera, n es la relación de los índices de refracción dentro y fuera de la esfera, y λ la longitud de onda de la luz.

Este conjunto de ecuaciones fue descrito por primera vez por van de Hulst en (1957).

Matemáticas

La dispersión por una nanopartícula esférica se resuelve exactamente independientemente del tamaño de la partícula. Consideramos la dispersión por una onda plana propagando a lo largo de la z-eje polarizado a lo largo del x-Eje. Permeabilidades dieléctricas y magnéticas de una partícula son ε ε 1{displaystyle varepsilon ¿Qué? y μ μ 1{displaystyle mu _{1}}, y ε ε {displaystyle varepsilon } y μ μ {displaystyle mu } para el medio ambiente.

Para resolver el problema de dispersión, primero escribimos las soluciones de la ecuación vectorial de Helmholtz en coordenadas esféricas, ya que los campos dentro y fuera de las partículas deben satisfacerla. Ecuación de Helmholtz:

Silencio Silencio 2E+k2E=0,Silencio Silencio 2H+k2H=0.{displaystyle nabla ^{2}mathbf {E} +{2}mathbf {E} =0,quad nabla ^{2}mathbf {H} +{2}mathbf {H} =0.}

Además de la ecuación de Helmholtz, los campos deben satisfacer las condiciones Silencio Silencio ⋅ ⋅ E=Silencio Silencio ⋅ ⋅ H=0{displaystyle nabla cdot mathbf {E} =nabla cdot mathbf {H} =0} y Silencio Silencio × × E=i⋅ ⋅ μ μ H{displaystyle nabla times mathbf {E} =iomega mu mathbf {H}, Silencio Silencio × × H=− − i⋅ ⋅ ε ε E{displaystyle nabla times mathbf {H} =-iomega varepsilon mathbf {E}. Los armónicos esféricos vectoriales poseen todas las propiedades necesarias, introducidas de la siguiente manera:

Moemn=Silencio Silencio × × ()r↑ ↑ oemn){displaystyle mathbf {M} _{e}_{o}mn}=nabla times left(mathbf {r} psi _{e}_{o}mn}right)}- armónicos magnéticos (TE),

Noemn=Silencio Silencio × × Moemnk{displaystyle mathbf {N} _{e}_{o}mn={frac} {nabla times mathbf {fnK} {fn}} {fnK}}} {fnK}}} {fn}}} {fn}} {fn}}}} {fn}}}} {fn}}}}}}}}}}} {fn}}}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}- armónicos eléctricos (TM),

dónde

↑ ↑ emn=#⁡ ⁡ mφ φ Pnm()#⁡ ⁡ Silencio Silencio )zn()kr),{displaystyle {psi _{emn}=cos mvarphi P_{n}{m}(cos vartheta)z_{n} {}}}}

↑ ↑ omn=pecado⁡ ⁡ mφ φ Pnm()#⁡ ⁡ Silencio Silencio )zn()kr),{displaystyle {psi _{omn}=sin mvarphi P_{n}{m}(cos vartheta)z_{n} {}}}}

y Pnm()#⁡ ⁡ Silencio Silencio ){displaystyle P_{n} {m}(cos theta)}- Polinomios Legendre asociados, y zn()kr){displaystyle z_{n}({k}r)}- cualquiera de las funciones esféricas de Bessel.

A continuación, expandimos la onda plana incidente en armónicos esféricos vectoriales:

Einc=E0eikr#⁡ ⁡ Silencio Silencio ex=E0.. n=1JUEGO JUEGO in2n+1n()n+1)()Mo1n()1)()k,r)− − iNe1n()1)()k,r)),Hinc=− − k⋅ ⋅ μ μ E0.. n=1JUEGO JUEGO in2n+1n()n+1)()Me1n()1)()k,r)+iNo1n()1)()k,r)).{displaystyle {begin{aligned}mathbf {E} {fn} {fnK} {fn}fnK}fnK}} {fn}} {fn}}}} - ¿Qué? {fn} {fnfnn}}nn}nnnnnn}nnnnnnn}left(mathbf {M} _{o1n}{(1)}(k,mathbf {n})-imathbf {n} {cH00} {cH00cH00cH00}cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}cH00cH00cH00cH00cH {H} _{inc} { k}{omega mu }E_{0}sum {fn} {fn} {fn} {fn} {fnn}}}left(mathbf {M} _{e1n} {cn} {cn} {cncHFF}imathbf {N} _{o1n} {} {cn} {cHFF} {f}}}}}}}}}}} {f}fn}}}}}}}}}}}}} {f} {f} {f}}}}}f}}}}n}}}}}}}}}}}}}}}} {f} {f}}}} {n} {f}} {n}}}}}}}}n}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}

Aquí el superscript ()1){displaystyle (1)} significa que en la parte radial de las funciones ↑ ↑ oemn{displaystyle psi _{e}_{o}mn} son las funciones esféricas de Bessel del primer tipo. Los coeficientes de expansión se obtienen tomando integrales de la forma

∫ ∫ 02π π ∫ ∫ 0π π Einc⋅ ⋅ Moemn()1)pecado⁡ ⁡ Silencio Silencio dSilencio Silencio dφ φ ∫ ∫ 02π π ∫ ∫ 0π π SilencioMoemn()1)Silencio2pecado⁡ ⁡ Silencio Silencio dSilencio Silencio dφ φ .{displaystyle {frac {int}{2pi}int ¿Qué? }Mathbf {E} _{inc}cdot mathbf {M} _{e}mn}{(1)}sin theta dtheta dvarphi ##{int _{0} {2pi}int ¿Qué?.. {M} _{e}_{o}mn}{(1)}derecho a la vida {2}sin theta dtheta dvarphi }}

En este caso, todos los coeficientes en mل ل 1{displaystyle mneq 1} son cero, ya que el integral sobre el ángulo φ φ {displaystyle varphi } en el numerador es cero.

Entonces se imponen las siguientes condiciones:

1. Condiciones de interfaz en el límite entre la esfera y el medio ambiente (que nos permiten relacionar los coeficientes de expansión del incidente, los campos internos y dispersos)
2. La condición de que la solución esté ligada al origen (por lo tanto, en la parte radial de las funciones generadoras ↑ ↑ oemn{displaystyle psi _{e}_{o}mn}, las funciones esféricas de Bessel del primer tipo se seleccionan para el campo interno),
3. Para un campo disperso, la asintotica en el infinito corresponde a una onda esférica divergente (en conexión con esto, para el campo disperso en la parte radial de las funciones generadoras ↑ ↑ oemn{displaystyle psi _{e}_{o}mn} las funciones esféricas de Hankel del primer tipo son elegidos).

Los campos dispersos se escriben en términos de una expansión armónica vectorial como

Es=.. n=1JUEGO JUEGO En()ianNe1n()3)()k,r)− − bnMo1n()3)()k,r)),{displaystyle mathbf {E} _{s}=sum ¿Qué? {fn} {fn}(k,mathbf {r})-b_{n}mathbf {m} _{o1n}{(3)}(k,mathbf {r})right),}} {fn} {} {fn}} {f}}}} {derech}}}}}

Hs=k⋅ ⋅ μ μ .. n=1JUEGO JUEGO En()anMe1n()3)()k,r)+ibnNo1n()3)()k,r)).{displaystyle mathbf {H} {k}{omega mu}sum _{n=1}{infty }E_{n}left(a_{n}mathbf {M} _{e1n} {k,mathbf {r})+ib_{n}mathbf {N} _{o1n} {(3)}(k,mathbf {r})right).}

Aquí el superscript ()3){displaystyle (3)} significa que en la parte radial de las funciones ↑ ↑ oemn{displaystyle psi _{e}_{o}mn}son las funciones esféricas de Hankel del primer tipo (las de la segunda clase tendrían ()4){displaystyle (4)}), y En=inE0()2n+1)n()n+1){displaystyle ¿Qué?,

Campos internos:

E1=.. n=1JUEGO JUEGO En()− − idnNe1n()1)()k1,r)+cnMo1n()1)()k1,r)),{displaystyle mathbf {E} _{1}=sum ¿Qué? }E_{n}left(-id_{n)mathbf {N} _{e1n}{(1)}(k_{1},mathbf {r})+c_{n}mathbf {M} _{o1n}{(1)}(k_{1},mathbf {r})right),}}

H1=− − k1⋅ ⋅ μ μ 1.. n=1JUEGO JUEGO En()dnMe1n()1)()k1,r)+icnNo1n()1)()k1,r)).{displaystyle mathbf {H}{1}={frac} {K_{1}{omega ################################################################################################################################################################################################################################################################ ¿Qué? }E_{n}left(d_{n}mathbf {M} _{1} {} {cn} {cn}cn}n}n}n}mn} {cn} {cn} {cn} {cn} {cn} {cHFF}cHFF}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}}cH00}cH00}cH00}cH }

k=⋅ ⋅ cn{textstyle k={frac {omega } {c}n} es el vector de onda fuera de la partícula k1=⋅ ⋅ cn1{textstyle k_{1}={frac {omega } {c} {n_{1}}}es el vector de onda en el medio del material de partículas, n{displaystyle n} y n1{displaystyle No. son los índices refractivos del medio y la partícula.

Después de aplicar las condiciones de interfaz, obtenemos expresiones para los coeficientes:

cn()⋅ ⋅ )=μ μ 1[*** *** hn()*** *** )].jn()*** *** )− − μ μ 1[*** *** jn()*** *** )].hn()*** *** )μ μ 1[*** *** hn()*** *** )].jn()*** *** 1)− − μ μ [*** *** 1jn()*** *** 1)].hn()*** *** ),{fn} {fn} {fn} {fn}fnh}nh} {fn} {fn} {fn}fn} {fn}fnh}fnh} {cH00}}nh} {nh}nh} {cH00}}nh}nh}nh} {fnh} {nh}h}h}nh}h}h} {h}h}h}hnh}h}h}h}hnh}hnhnh}h}h}h}h}hnhnh}h}h}h}h}h}h}h}h}h}h}h}h}h}hnhnhnhnhnh}hnhnh}h}h}h}hnh

dn()⋅ ⋅ )=μ μ 1n1n[*** *** hn()*** *** )].jn()*** *** )− − μ μ 1n1n[*** *** jn()*** *** )].hn()*** *** )μ μ n12[*** *** hn()*** *** )].jn()*** *** 1)− − μ μ 1n2[*** *** 1jn()*** *** 1)].hn()*** *** ),{displaystyle d_{n}(omega)={frac {mu} - ¿Por qué? ¿Por qué? ¿Qué? ¿Por qué? ¿Qué?

bn()⋅ ⋅ )=μ μ 1[*** *** jn()*** *** )].jn()*** *** 1)− − μ μ [*** *** 1jn()*** *** 1)].jn()*** *** )μ μ 1[*** *** hn()*** *** )].jn()*** *** 1)− − μ μ [*** *** 1jn()*** *** 1)].hn()*** *** ),{fn} {fn} {fnh}fn} {fnh}n} {fn} {fn} {fn} {fn} {fn} {fn}}nh} {cH00}n}} {cH00} {cH00}}}cH00} {cH00}}}}} {fn}}}}}}} {n}}}}}}}}}}n}} {cH} {f} {cH}}}}} {cH}}}}}}}}}}}} {cH} {f} {f}}}} {f} {f}} {f}}}}}}}}} {f} {f}}f} {f}}}}}}}}}}}}}f}}}}}f}}}}}}}}}}}}}}}}

an()⋅ ⋅ )=μ μ n12[*** *** jn()*** *** )].jn()*** *** 1)− − μ μ 1n2[*** *** 1jn()*** *** 1)].jn()*** *** )μ μ n12[*** *** hn()*** *** )].jn()*** *** 1)− − μ μ 1n2[*** *** 1jn()*** *** 1)].hn()*** *** ),{displaystyle a_{n}(omega)={frac {mu} ################################################################################################################################################################################################################################################################ ¿Por qué? ¿Por qué? ¿Qué? ¿Por qué? ¿Qué?

dónde

*** *** =ka,{displaystyle rho =ka,}

*** *** 1=k1a{displaystyle rho ¿Qué? con a{displaystyle a} ser el radio de la esfera.

jn{displaystyle J_{n} y hn{displaystyle H_{n}representan las funciones esféricas de Bessel y Hankel del primer tipo, respectivamente.

Secciones transversales de dispersión y extinción

Valores comúnmente calculados utilizando La teoría de Mie incluye coeficientes de eficiencia para la extinción Qe{displaystyle Q_{e}, dispersando Qs{displaystyle Q_{s}, y absorción Qa{displaystyle Q_{a}. Estos coeficientes de eficiencia son ratios de la sección transversal del proceso respectivo, σ σ i{displaystyle sigma _{i}, al área protegida de partículas, Qi=σ σ iπ π a2{displaystyle Q_{i}={frac {sigma _{i} {s} {s}}} {s}} {s}} {s}}} {s}}} {s}}}} {s}}}}}} {s}}}}}}}} {s}}}}} {s}}}}} {s}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {s}}}}}}}}}}}}}}} {s}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {, donde a es el radio de partículas. Según la definición de extinción,

σ σ e=σ σ s+σ σ a{displaystyle sigma _{e}=sigma ¿Qué? y Qe=Qs+Qa{displaystyle ¿Qué?.

Los coeficientes de dispersión y extinción se pueden representar como la serie infinita:

Qs=2k2a2.. n=1JUEGO JUEGO ()2n+1)()SilencioanSilencio2+SilenciobnSilencio2){displaystyle Q_{s}={frac {2}{2}a}a} {2}} {2}}} {2}}}} {c}}}}} {c}} {2}}}} {}}}}}}}}}}}} {}}}}}} {}}}}} {}}}}} {}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} ¿Qué? () Silencio.

Qe=2k2a2.. n=1JUEGO JUEGO ()2n+1)R R ()an+bn){displaystyle Q_{e}={frac {2}{2}a}a} {2}} {2}}} {2}}}} {c}}}}} {c}} {2}}}} {}}}}}}}}}}}} {}}}}}} {}}}}} {}}}}} {}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} ¿Por qué?

Las contribuciones en estas sumas, indexadas por n, corresponden a los órdenes de una expansión multipolar con n = 1 siendo el término dipolar, n = 2 siendo el término cuadripolar, y así sucesivamente.

Aplicación a partículas más grandes

Si el tamaño de la partícula es igual a varias longitudes de onda en el material, entonces los campos dispersos tienen algunas características. Además, hablaremos sobre la forma del campo eléctrico, ya que el campo magnético se obtiene tomando el rotor.

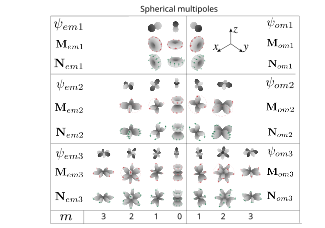
Todos los coeficientes Mie dependen de la frecuencia y tienen máximos cuando el denominador está cerca de cero (la igualdad exacta a cero se logra para frecuencias complejas). En este caso, es posible que la contribución de un armónico específico domina en la dispersión. Luego a grandes distancias de la partícula, el patrón de radiación del campo disperso será similar al patrón de radiación correspondiente de la parte angular de los armónicos esféricos vectoriales. Los armónicos Noem1{displaystyle mathbf {N} {fn} {fn} {fn} {fn}} {fn}} {fn} {fn}} {fn}} {fn}}} {fn}} {fn}}}}} {\fnK}}}}}}}}}}}}}}}}}} {\f}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} corresponde a dipoles eléctricos (si la contribución de este armónico domina en la expansión del campo eléctrico, entonces el campo es similar al campo de dipolo eléctrico), Moem1{displaystyle mathbf {M} _{e}_{o}m1} corresponde al campo eléctrico del dipolo magnético, Noem2{displaystyle mathbf {N} {fn} {fn} {fn} {fn} {fn}} {fn} {fn}} {fn}}} {fn}}} {fn}} {fn}}}}}} {\fn}}} {\fn}}}}}}}} {\\\\}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} y Moem2{displaystyle mathbf {M} _{e}_{o}m2} - quadrupoles eléctricos y magnéticos, Noem3{displaystyle mathbf {N} {fn} {fn} {fn}} {fn} {fn}} {fn} {fn}} {fn}} {fn}}} {fn}}} {fn}}}}}} {\fn}}}} {\fn}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} y Moem3{displaystyle mathbf {M} _{e}_{o}m3} - octupoles, y así sucesivamente. La máxima de los coeficientes de dispersión (así como el cambio de su fase a π π {displaystyle pi}) se llaman resonancias multipole.

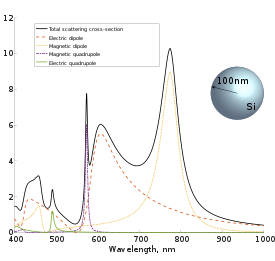
La dependencia de la sección transversal de dispersión de la longitud de onda y la contribución de resonancias específicas depende en gran medida del material de las partículas. Por ejemplo, para una partícula de oro con un radio de 100 nm, la contribución del dipolo eléctrico a la dispersión predomina en el rango óptico, mientras que para una partícula de silicio hay resonancias magnéticas pronunciadas de dipolo y cuadrupolo. Para partículas de metal, el pico visible en la sección transversal de dispersión también se denomina resonancia de plasmón localizada.

En el límite de partículas pequeñas o longitudes de onda largas, la contribución del dipolo eléctrico domina en la sección transversal de dispersión.

Otras direcciones de la onda plana incidente

En el caso de onda plana polarizada x-, incidente a lo largo del eje z, las descomposiciones de todos los campos contenían solo armónicos con m= 1, pero para una onda incidente arbitraria este no es el caso. Para una onda plana girada, los coeficientes de expansión se pueden obtener, por ejemplo, utilizando el hecho de que durante la rotación, los armónicos esféricos vectoriales se transforman entre sí mediante matrices D de Wigner.

En este caso, el campo disperso se descompondrá por todos los armónicos posibles:

Es=.. n=1JUEGO JUEGO .. m=0nE0()DMemnMemn()3)()k,r)+DMomnMomn()3)()k,r)+DNemnNemn()3)()k,r)+DNomnNomn()3)()k,r)){displaystyle mathbf {E} {fn} {fnfn}fnfnfnfnfnfnK}s} ¿Qué? {fn} {fn} {fnMicrosoft} {fn}} {cH00}} {cH00}} {cH00} {cH00}} {cH00}} {cH00}} {cH00}} {cH00}} {cH00} {cH00}} {cH00}}}} {cH00}}}}}}}}}}}} {cH00}}}}} {cH00} {cH00}}}} {cH00}}} {cH00}}}}}}}}}}}}}}}}}}}}}}}}}} {cH}}}}}}}}}}}}}}}}} {ccccH}}} {}}}}}}}}}}} {cH}}}}}}}}}}}}}}}}}}}} {cH

Entonces la sección transversal de dispersión se expresará en términos de los coeficientes de la siguiente manera:

Csca=2π π π π a2k2.. n=1JUEGO JUEGO n()n+1)()2n+1)× × [.. m=1n()n+m)!()n− − m)!()SilencioDMemnSilencio2+SilencioDMomnSilencio2+SilencioDNemnSilencio2+SilencioDNomnSilencio2)+2SilencioDMe0nSilencio2+2SilencioDNe0nSilencio2].{displaystyle ¿Qué? - ¿Qué? _{n=1}{infty }{frac {n(n+1)}{(2n+1)}times left[sum limits ################################################################################################################################################################################################################################################################

Efecto Kerker

El efecto Kerker es un fenómeno de direccionalidad de dispersión, que se produce cuando se presentan diferentes respuestas multipolares y no despreciables.

En 1983, en el trabajo de Kerker, Wang y Giles la dirección de la dispersión por partículas con μ μ ل ل 1{displaystyle mu neq 1} fue investigado. En particular, se demostró que para partículas hipotéticas con μ μ =ε ε {displaystyle mu =varepsilon } La dispersión hacia atrás está completamente suprimida. Esto se puede ver como una extensión a una superficie esférica de los resultados de Giles y Wild para la reflexión en una superficie plana con índices refractivos iguales donde la reflexión y la transmisión son constantes e independientes del ángulo de incidencia.

Además, las secciones transversales de dispersión en las direcciones hacia adelante y hacia atrás se expresan simplemente en términos de coeficientes de Mie:

Cscahacia atrás=1a2k2Silencio.. n=1JUEGO JUEGO ()2n+1)()− − 1)n()an− − bn)Silencio2Cscapara el futuro=1a2k2Silencio.. n=1JUEGO JUEGO ()2n+1)()an+bn)Silencio2{displaystyle {begin{aligned}C_{sca}{text{backward={frac} {1}{a^{2}k^{2}}left permanentlysum {fnfn} {fn} {fnfn}} {fn}} {fn} {fn} {fn}fn} {fn}fnfn}fnfnfn}} {fnfnfn}}}fnfnfnfnfnfnfnfn}}}fnfnfnfnfnfnfnfnfnfncH00fnfnfncn}}}fnKfnfnfn}fnKfnnnnnnnnnnnnnnnnnnnnnnnnnnnnfnfnnnnnnnnnnnnnnnnnnnnnnn}}ccccnnnn}}}c} {1}{a^{2}k^{2}}left permanentlysum ¿Por qué?

Para ciertas combinaciones de coeficientes, las expresiones anteriores se pueden minimizar.

Así que, por ejemplo, cuando términos con 1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/> puede ser descuidado (dipole aproximación), ()a1− − b1)=0{displaystyle (a_{1}-b_{1}=0}, corresponde al mínimo en backscattering (dipoles magnéticos y eléctricos son iguales en magnitud y están en fase, esto también se llama primer Kerker o Confección de intensidad cero hacia atrás). Y ()a1+b1)=0{displaystyle (a_{1}+b_{1})=0}corresponde al mínimo en la dispersión delantera, esto también se llama segunda condición Kerker (o estado de intensidad avanzada cercano a cero). Del teorema óptico, se muestra que para una partícula pasiva ()a1=− − b1){displaystyle (a_{1}=-b_{1}} no es posible. Para la solución exacta del problema, es necesario tener en cuenta las contribuciones de todas las multipoles. La suma de los dipoles eléctricos y magnéticos forma fuente Huygens

Para las partículas dieléctricas, la máxima dispersión hacia adelante se observa en longitudes de onda más largas que la longitud de onda de la resonancia dipolar magnética, y la máxima dispersión hacia atrás en las más cortas.

Más tarde, se encontraron otras variedades del efecto. Por ejemplo, el efecto Kerker transversal, con casi completo simultáneo supresión de campos dispersos hacia adelante y hacia atrás (patrones de dispersión lateral), efecto Kerker optomecánico, en dispersión acústica y también encontrado en plantas.

También hay un video corto en YouTube con una explicación del efecto.

Función Dyadic Green de una esfera

La función de Green es una solución a la siguiente ecuación:

Silencio Silencio × × Silencio Silencio × × G^ ^ ()⋅ ⋅ ,r,r.)=()⋅ ⋅ c)2ε ε ()r,⋅ ⋅ )G^ ^ ()⋅ ⋅ ,r,r.)+1^ ^ δ δ ()r− − r.),{displaystyle nabla times nabla times {bf {hat {G}}(omegamathbf {r}mathbf {r} ')=left({frac {omega {fnK}f} {fnh} {fnh}fnh} {f} {f} {f} {f} {fn} {f}fnh}fn}fnh}fnh}f}fnh}f}fnhnhnh}f}

Donde 1^ ^ {displaystyle {hat {bf} {}}}— matriz de identidad ε ε ()r,⋅ ⋅ )=ε ε 1()⋅ ⋅ ){displaystyle varepsilon (mathbf {r}omega)=varepsilon _{1}(omega)} para <math alttext="{displaystyle rr.a{displaystyle r madea}<img alt="{displaystyle r, y ε ε ()r,⋅ ⋅ )=ε ε {displaystyle varepsilon (mathbf {r}omega)=varepsilon } para a}" xmlns="http://www.w3.org/1998/Math/MathML">r■a{displaystyle r]a}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/111ddf834122e07317295953466f9e8aaaf242a0" style="vertical-align: -0.338ex; width:5.377ex; height:1.843ex;"/>. Como todos los campos son vectoriales, la función verde es una matriz de 3 por 3 y se llama dyadic. Si polarización P()r){displaystyle mathbf {} (mathbf {r})} es inducido en el sistema, cuando los campos están escritos como

E⋅ ⋅ ()r)=⋅ ⋅ 2μ μ ∫ ∫ VdV.G^ ^ ()r,r.,k)P⋅ ⋅ ()r.){fnMitbf {} {fnMitbf {f}}=omega ^{2}mu int limits _{V}dV'{hat {bf {}} {bf {bf {f}}},k)mathbf {f} {f}f}cH00} {cH00}}} {cH00}}}}}f}}}}}cH00}}}cH00} {cH00}cH00} {cH00}cH00}cH00}}}}}}}}}}}}}}}}}}}}}cH00} {f} {cH00}cH00} {cH00} {cH00}cH00}cH00}cH00}cH00}cH00}}}}}}}}}}}}}}}}}}}}}}

Al igual que los campos, la función de Green se puede descomponer en armónicos esféricos vectoriales. Función de Dyadic Green de un espacio libre:

<math alttext="{displaystyle {begin{aligned}&{hat {bf {G}}}^{0}({mathbf {r}mathbf {r} ',k})\{}={}&{frac {mathbf {e_{r}} otimes mathbf {e_{r}} }{k^{2}}}delta (mathbf {r} -mathbf {r} ')+{frac {ik}{4pi }}sum _{n=1}^{infty }sum _{m=0}^{n}(2-delta _{m,0}){frac {2n+1}{n(n+1)}}{frac {(n-m)!}{(n+m)!}}cdot {}\&quad {begin{cases}left(left(mathbf {M} _{emn}^{(1)}[k,mathbf {r} ]otimes {mathbf {M} }_{emn}^{(3)}[k,mathbf {r} ']+mathbf {M} _{omn}^{(1)}[k,mathbf {r} ]otimes {mathbf {M} }_{omn}^{(3)}[k,mathbf {r} ']right)+left({mathbf {N} }_{emn}^{(1)}[k,mathbf {r} ]otimes {mathbf {N} }_{emn}^{(3)}[k,mathbf {r} ']+mathbf {N} _{omn}^{(1)}[k,mathbf {r} ]otimes {mathbf {N} }_{omn}^{(3)}[k,mathbf {r} ']right)right),&{text{if }}rr'end{cases}}end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">G^ ^ 0()r,r.,k)=er⊗ ⊗ erk2δ δ ()r− − r.)+ik4π π .. n=1JUEGO JUEGO .. m=0n()2− − δ δ m,0)2n+1n()n+1)()n− − m)!()n+m)!⋅ ⋅ {}()()Memn()1)[k,r]⊗ ⊗ Memn()3)[k,r.]+Momn()1)[k,r]⊗ ⊗ Momn()3)[k,r.])+()Nemn()1)[k,r]⊗ ⊗ Nemn()3)[k,r.]+Nomn()1)[k,r]⊗ ⊗ Nomn()3)[k,r.])),sir.r.()()Memn()3)[k,r]⊗ ⊗ Memn()1)[k,r.]+Momn()3)[k,r]⊗ ⊗ Momn()1)[k,r.])+()Nemn()3)[k,r]⊗ ⊗ Nemn()1)[k,r.]+Nomn()3)[k,r]⊗ ⊗ Nomn()1)[k,r.])),sir■r.{begin{f} {bf} {f}} {f} {f} {f} {f} {f}f} {f}f}f}f}}\f}}\fn}}\\\f}= {f}}}}\\f}}}}}}\\\f}}\\\\\\\\\\\\f}}\\\\\\f}}}}\\\\\f}}}}}}\\\\\\\\fn}}\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\ {fnK} otimes mathbf {e_{r} } {k^{2}}delta {fn} {fn} {fn} {fn} {fnfn} {fn} {fn} {fn} {fn} {fn} {fn}} {fnfn} {fn}} {fnf}} {fnfnf} {fnfnf}fnfnfnfnhnhnfnhnhnhnf}}}}} {fnfnfnfnhnhnhnfnhnhnfnfnhnhnhnhnhnhnhnhnhnhnhnhn}}}}}}} {fnf} {fnh00}fnhnh00}fnfnhnhnhnhnhnf}fnhnhnhnhnhnhnhnhn ################################################################################################################################################################################################################################################################ ### Otimes {mathbf {N}_{emn} {wk,mathbf {r} ']+mathbf {N} _{omn}{(1) {k,mathbf {r}otimes {mathbfffff} {fn} {fn} {fnh} {fnfnh}} {fnh}f} {fn} {cH00} {cH00}cH00}cH00}cH00}cH00} {cH00}cH00}cH00cH00}cH00cH00}cH00cH00}cH00cH00}cH00}cH00cH00cH00cH00cH00}cH00cH00cH00}cH00cH00}cH00}cH00cH00}cH00}cH00}cH00}cH00}cH00cH00cH00cH00}cH00}cH00cH00cH00}cH00cH00cH00}cH00cH #otimes {mathbf {N}_{emn}{(1)}[k,mathbf {r}mathbf {N} _{omn}} {k,mathbf {r} {r} #otimes {mathbf {N}_{omn}{(1)}[k,mathbf {r}right)right), limitándose {text{if}}r confianzar'end{cases}}end{aligned}}}}}}} {fnunció}<img alt="{displaystyle {begin{aligned}&{hat {bf {G}}}^{0}({mathbf {r}mathbf {r} ',k})\{}={}&{frac {mathbf {e_{r}} otimes mathbf {e_{r}} }{k^{2}}}delta (mathbf {r} -mathbf {r} ')+{frac {ik}{4pi }}sum _{n=1}^{infty }sum _{m=0}^{n}(2-delta _{m,0}){frac {2n+1}{n(n+1)}}{frac {(n-m)!}{(n+m)!}}cdot {}\&quad {begin{cases}left(left(mathbf {M} _{emn}^{(1)}[k,mathbf {r} ]otimes {mathbf {M} }_{emn}^{(3)}[k,mathbf {r} ']+mathbf {M} _{omn}^{(1)}[k,mathbf {r} ]otimes {mathbf {M} }_{omn}^{(3)}[k,mathbf {r} ']right)+left({mathbf {N} }_{emn}^{(1)}[k,mathbf {r} ]otimes {mathbf {N} }_{emn}^{(3)}[k,mathbf {r} ']+mathbf {N} _{omn}^{(1)}[k,mathbf {r} ]otimes {mathbf {N} }_{omn}^{(3)}[k,mathbf {r} ']right)right),&{text{if }}rr'end{cases}}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6f92e7ac0dc59a93030ac8b1351c8b94ef54326a" style="vertical-align: -9.671ex; width:134.301ex; height:20.509ex;"/>

En presencia de una esfera, la función de Green también se descompone en armónicos esféricos vectoriales. Su apariencia depende del ambiente en el que los puntos r{displaystyle mathbf {r} y r.{displaystyle mathbf {r} están ubicados.

Cuando ambos puntos están fuera de la esfera (a,r'>a}" xmlns="http://www.w3.org/1998/Math/MathML">r■a,r.■a{displaystyle r confíaa,r' confíaa}a,r'>a}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9925a17a5d6f1d915c28d166c8f200cad83fd7ab" style="vertical-align: -0.671ex; width:12.473ex; height:2.843ex;"/>):

G^ ^ 00()r,r.,k,k1)=G^ ^ 0()r,r.,k)+ik4π π .. n=1JUEGO JUEGO .. m=0n()2− − δ δ m,0)2n+1n()n+1)()n− − m)!()n+m)!⋅ ⋅ ()an()0)()⋅ ⋅ )()Moemn()3)[k,r]⊗ ⊗ Moemn()3)[k,r.])+bn()0)()⋅ ⋅ )()Noemn()3)[k,r]⊗ ⊗ Noemn()3)[k,r.])){begin{begin{hat {bf} {bf}} {m} {\mhbf {}m}mthbf {r} ',k,k_{1}}}\ {}={} {}} {f} {f}} {f}}}} {f} {f}}}}}}}}}}} {f}}}}}}}}}}} {\m}}}}}}}}} {\\}}}}}}}}}}}}} {\\\\\\\\\\\m}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fn} {f} {f} {f}} {f}f} {f}} {f} {f}} {f}} {fn}} {fn} {fn}} {fn}} {f}} {f}} {f} {cH00}}}} {f}}}}} {f} {f} {f}}}}}}}} {f} {f}}}f} {f} {f} {f}}}}}}}}}f} {f} {f}f}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {f}}}}}}}}f} {f}}}f} {f}}f}}}}}}}}}f} {f}f}}}}}}}}}} {fn} {fn} {cH00} {cH00}} {cH00} {cH00}}mn} {cH00} {cH00}cH00} {cH00} {cH00} {cH00} {cH00}} {cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00} {cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}}}}cH00 {cH00} {cH00} {cH00} {cH00} {cH00FF} {cH00}} {cH00}} {cH00}} {cH00}}}} {cH00}}}}

donde los coeficientes son:

an()0)()⋅ ⋅ )=μ μ /μ μ 1[*** *** 1jn()*** *** 1)].jn()*** *** )− − [*** *** jn()*** *** )].jn()*** *** 1)[*** *** hn()*** *** )].jn()*** *** 1)− − μ μ /μ μ 1[*** *** 1jn()*** *** 1)].hn()*** *** ),bn()0)()⋅ ⋅ )=n2μ μ 1/μ μ [*** *** 1jn()*** *** 1)].jn()*** *** )− − n12[*** *** jn()*** *** )].jn()*** *** 1)n12[*** *** hn()*** *** )].jn()*** *** 1)− − n2μ μ 1/μ μ [*** *** 1jn()*** *** 1)].hn()*** *** ).{fnMiega)} {fnMigando)} {fnMigando)} {fnMicrosoft Sans Serif} {fn}mn}fnMicrosoft Sans Serif} ¿Por qué? ¿Por qué? {1}/muleft[rho] ¿Qué? ¿Por qué?

Cuando ambos puntos están dentro de la esfera (<math alttext="{displaystyle r<a,r'r.a,r..a{displaystyle r madea,r'cantaa}<img alt="{displaystyle r<a,r')

G^ ^ 11()r,r.,k,k1)=G^ ^ 0()r,r.,k1)+ik14π π .. n=1JUEGO JUEGO .. m=0n()2− − δ δ m,0)2n+1n()n+1)()n− − m)!()n+m)!⋅ ⋅ ()cn()1)()⋅ ⋅ )()Moemn()1)[k1,r]⊗ ⊗ Moemn()1)[k1,r.])+dn()1)()⋅ ⋅ )()Noemn()1)[k1,r]⊗ ⊗ Noemn()1)[k1,r.])),{fnMicrosoft Sans Serif} {f}} {f} {f} {f} {f} {f} {f} {f} {f}} {f}}} {f}}} {f}}} {c} {f} {f}}}}} {f} {f}}}f}f}}} {f}}}}}}}}}}}}}}}}} {f} {f}}}} {c}}}}}}}}}}}} {f} {ccf} {f}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}} {cccccccf}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}} {fn} {fn} {fn} {fn} {f} {fn} {fn} {fn} {fn} {f} {fn} {fn} {fn} {fn} {cccH00}} {ccH00}cH00} {cH00}} {cH00}}}}} {ccccccH00} {ccccccccccccccH00}cccH00}cccccccccccccH00} {cH00cccH00ccH00} {cH00}} {cH00}} {cH00}ccH00}ccH00}}ccc {M}_{e}_{o}mn}{(1)}[k_{1},mathbf {r} ']right)+d_{n}{(1)}(omega)left({mathbfff {N}_{e}_{o} {{(1)}[k_{1},mathbf {r}otimes {mathbf {N}_{e}_{o} {{(1)}[k_{1},mathbf {r}right)right),end{aligned}}

Coeficientes:

cn()1)()⋅ ⋅ )=μ μ 1/μ μ [*** *** hn()*** *** )].hn()*** *** 1)− − [*** *** 1hn()*** *** 1)].hn()*** *** )[*** *** 1jn()*** *** 1)].hn()*** *** )− − μ μ 1/μ μ [*** *** hn()*** *** )].jn()*** *** 1),dn()1)()⋅ ⋅ )=n12μ μ /μ μ 1[*** *** hn()*** *** )].hn()*** *** 1)− − n2[*** *** 1hn()*** *** 1)].hn()*** *** )n2[*** *** 1jn()*** *** 1)].hn()*** *** )− − n12μ μ /μ μ 1[*** *** hn()*** *** )].jn()*** *** 1).{displaystyle {begin{aligned}c_{{(1)}(omega) ¿Por qué? ¿Por qué? ¿Por qué? {n_{1}{2}mu _{1}left [rho h_{n}(rho)right]'h_{n}(rho _{1})-n^{2}left[rho] ¿Por qué? - ¿Por qué?

La fuente está dentro de la esfera y el punto de observación está fuera (a,r'r■a,r..a{displaystyle r títuloa,r'traducidoa}a,r'):

G^ ^ 01()r,r.,k,k1)=ik14π π .. n=1JUEGO JUEGO .. m=0n()2− − δ δ m,0)2n+1n()n+1)()n− − m)!()n+m)!⋅ ⋅ ()an()1)()⋅ ⋅ )()Moemn()3)[k,r]⊗ ⊗ Moemn()1)[k1,r.])+bn()1)()⋅ ⋅ )()Noemn()3)[k,r]⊗ ⊗ Noemn()1)[k1,r.])){begin{begin{hat {bf {bf}} {f} {f} {\f}\mhbf {f}f}cH00}}}\\f}= {f} {f}}}} {f} {f}}\f}\f}f}}}}\\\\f}}}}\\\\\\f}}\\\\\\\\\\\\\\\\\f}\\\\\\\\\\\\\\fn\\\\\\\\\fn\\\\\\\\fn\\\fn}\\fnfn\\\ {fn} {fn} {fn} {fn} {fnf} {fn} {fn} {f} {fn} {fn} {f} {fn} {fnf}} {m} {cH00}}} {cH00} {cH00} {cH00}}} {cH00}}}} {b}}}}}}ccb}} {b} {f} {b}ccccccccccccccH00ccccccccccccH00} {cH00cccH00cH00}cccH00}cH00}ccH00}}ccH00}ccH00} {ccc {M}_{e}_{o} {{(1)}[k_{1},mathbf {r} '])+b_{{(1)}(omega)left(mathbf {N} _{o}mn}{(3)} {k,mathbf {r} {f} {f} {f} {f} {f}} {f}f}}} {f}f}}}}f}f}f}} {f} {f} {f}} {f}f} {f}f}f}f}f}f}f}f}}}}f}f} {f}f} {f}}f}f} {f}f}f}f}}}f}f}f}f}f}f}f}f}f}f}f}}f}f} {N}_{e}_{o} {{(1)}[k_{1},mathbf {r}right)end{aligned}}

coeficientes:

an()1)()⋅ ⋅ )=[*** *** 1jn()*** *** 1)].hn()*** *** 1)− − [*** *** 1hn()*** *** 1)].jn()*** *** 1)[*** *** 1jn()*** *** 1)].hn()*** *** )− − μ μ 1/μ μ [*** *** hn()*** *** )].jn()*** *** 1),bn()1)()⋅ ⋅ )=nn1[*** *** 1jn()*** *** 1)].hn()*** *** 1)− − nn1[*** *** 1hn()*** *** 1)].jn()*** *** 1)n2μ μ 1/μ μ [*** *** 1jn()*** *** 1)].hn()*** *** )− − n12[*** *** hn()*** *** )].jn()*** *** 1).{fncipo {fn}a_{(1)}(omega) {fnMicroc {left[rho] ¿Por qué? ¿Por qué? ¿Por qué? ¿Por qué? ¿Por qué? {1}/muleft[rho] ¿Por qué?

La fuente está fuera de la esfera y el punto de observación está dentro (<math alttext="{displaystyle ra}" xmlns="http://www.w3.org/1998/Math/MathML">r.a,r.■a{displaystyle r madea,r'senta}<img alt="{displaystyle ra}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f7396ca62be0e172b88dc63a7043154a4c228f3e" style="vertical-align: -0.671ex; width:12.473ex; height:2.843ex;"/>)

G^ ^ 10()r,r.,k,k1)=ik4π π .. n=1JUEGO JUEGO .. m=0n()2− − δ δ m,0)2n+1n()n+1)()n− − m)!()n+m)!⋅ ⋅ ()cn()0)()⋅ ⋅ )()Moemn()1)[k,r]⊗ ⊗ Moemn()3)[k1,r.])+dn()0)()⋅ ⋅ )()Noemn()1)[k,r]⊗ ⊗ Noemn()3)[k1,r.])){begin{begin{hat {bf} {bf} {f} {f} {\f}\mhbf {r}mhbf {r} ',k,k_{1}}}\ {}={} {}} {f} {f}f}f}f}f} {f}f}}}}}}}}}}}}}}\\\\\\\\\\\\\f}}}}\\\\\\\\f}\\\\f}\\\\\\\\\fn\\\\\\\\\\\\fn\\\\\\\\\\\\\f}\\\fn {f} {f} {f} {f} {f}} {f} {f}} {f} {f} {f} {f}} {f}f} {f} {f} {f}} {m} {f} {f}}} {f}f} {f} {f}f}f} {f}f} {f}f}f}f}c}f} {f} {f}}f}}}}c}f} {f}f}f}f}f}f}f} {f}f}f}f} {f}f} {f} {f}f} {f}f}f}f} {f}f}f}f}f}f}f}f}f}f} {f}c}c {M}_{e}_{o} {} {k_{1},mathbf {r}'])+d_{n} {0}(omega)({mathbf {N}_{e}_{o}mn}{(1)} {k,mathbf {m} {cH00} {cH00} {cH00}}} {cH00}}} {cH00}} {cH00} {cH00}}}} {cH00}cH00}}}}}}cH00} {cH00}cH00}}cH00}cH00}}}}}cH00}cH00} {cH00}cH00}cH00} {cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00} {cH00} {fn} {fn} {cH00} {cH00} {cH00} {cHFF}m}}} {cH00}}} {cHFF}}} {cHFF}}} {cHFF}} {cH00}} {cH}}}}}}

coeficientes:

cn()0)()⋅ ⋅ )=[*** *** hn()*** *** )].jn()*** *** )− − [*** *** jn()*** *** )].hn()*** *** )[*** *** hn()*** *** )].jn()*** *** 1)− − μ μ /μ μ 1[*** *** 1jn()*** *** 1)].hn()*** *** ),dn()0)()⋅ ⋅ )=nn1[*** *** hn()*** *** )].jn()*** *** )− − nn1[*** *** jn()*** *** )].hn()*** *** )n12μ μ /μ μ 1[*** *** hn()*** *** )].jn()*** *** 1)− − n2[*** *** 1jn()*** *** 1)].jn()*** *** ).{fn} {fn} {fn}}n} {fn} {fn} {fn} {fn} {fn} {fn} {fn} {fn}fn} {cHFF}}n}nh} {fn}}nhnh} {fn}}fnh} {fnh}fnh}fnh}}}fnhnh}}fnh} {fnh}fnhnh} {fnhnhnhnhnhnhnhnhnhnhnhnh}fnhnhnhnhnhnhnh} {fnh}h}h}h}hnhnh}fnh}hnh}hnhnhnhnhnhnhnhnhnhnh}fnhnh}hnhn ¿Qué? ¿Por qué?

Códigos computacionales

Las soluciones de Mie se implementan en una serie de programas escritos en diferentes lenguajes informáticos, como Fortran, MATLAB y Mathematica. Estas soluciones resuelven una serie infinita y proporcionan como salida el cálculo de la función de fase de dispersión, las eficiencias de extinción, dispersión y absorción, y otros parámetros como los parámetros de asimetría o el par de radiación. Uso actual del término "solución Mie" indica una aproximación en serie a una solución de las ecuaciones de Maxwell. Hay varios objetos conocidos que permiten tal solución: esferas, esferas concéntricas, cilindros infinitos, grupos de esferas y grupos de cilindros. También se conocen soluciones en serie para la dispersión por partículas elipsoidales. A continuación se proporciona una lista de códigos que implementan estas soluciones especializadas:

• Códigos para la dispersión electromagnética por esferas: soluciones para una sola esfera, esferas recubiertas, esfera multicapa y racimo de esferas;
• Códigos para la dispersión electromagnética por cilindros – soluciones para un solo cilindro, cilindros multicapa y racimo de cilindros.

Una generalización que permite un tratamiento de partículas con formas más generales es el método de matriz T, que también se basa en una aproximación en serie a las soluciones de las ecuaciones de Maxwell.

Ver también enlaces externos para otros códigos y calculadoras.

Aplicaciones

La teoría de Mie es muy importante en la óptica meteorológica, donde las proporciones de diámetro a longitud de onda del orden de la unidad y mayores son características de muchos problemas relacionados con la neblina y la dispersión de nubes. Otra aplicación es la caracterización de partículas mediante medidas de dispersión óptica. La solución de Mie también es importante para comprender la apariencia de materiales comunes como la leche, el tejido biológico y la pintura de látex.

Ciencia atmosférica

La dispersión de Mie ocurre cuando los diámetros de las partículas atmosféricas son similares o mayores que las longitudes de onda de la luz. El polvo, el polen, el humo y las gotas de agua microscópicas que forman nubes son causas comunes de la dispersión de Mie. La dispersión de Mie ocurre principalmente en las porciones más bajas de la atmósfera, donde las partículas más grandes son más abundantes y domina en condiciones de nubosidad.

Detección y cribado del cáncer

La teoría de Mie se ha utilizado para determinar si la luz dispersada por el tejido corresponde a núcleos de células sanas o cancerosas mediante interferometría de baja coherencia con resolución angular.

Análisis de laboratorio clínico

La teoría de Mie es un principio central en la aplicación de ensayos basados en nefelometría, ampliamente utilizados en medicina para medir diversas proteínas plasmáticas. Se puede detectar y cuantificar una amplia gama de proteínas plasmáticas mediante nefelometría.

Partículas magnéticas

En las esferas magnéticas se producen una serie de efectos de dispersión electromagnética inusuales. Cuando la permitividad relativa es igual a la permeabilidad, la ganancia de retrodispersión es cero. Además, la radiación dispersada está polarizada en el mismo sentido que la radiación incidente. En el límite de partículas pequeñas (o de longitud de onda larga), pueden darse condiciones para una dispersión frontal cero, para una polarización completa de la radiación dispersada en otras direcciones y para una asimetría entre la dispersión frontal y la retrodispersión. El caso especial en el límite de partículas pequeñas proporciona casos especiales interesantes de polarización completa y asimetría de dispersión frontal a retrodispersión.

Metamaterial

La teoría de Mie se ha utilizado para diseñar metamateriales. Por lo general, consisten en compuestos tridimensionales de inclusiones metálicas o no metálicas incrustadas periódica o aleatoriamente en una matriz de baja permitividad. En tal esquema, los parámetros constitutivos negativos están diseñados para aparecer alrededor de las resonancias de Mie de las inclusiones: la permitividad efectiva negativa está diseñada alrededor de la resonancia del coeficiente de dispersión del dipolo eléctrico de Mie, mientras que la permeabilidad efectiva negativa está diseñada alrededor de la resonancia de Mie. El coeficiente de dispersión del dipolo magnético y el material doblemente negativo (DNG) están diseñados en torno a la superposición de resonancias de los coeficientes de dispersión del dipolo eléctrico y magnético de Mie. La partícula suele tener las siguientes combinaciones:

1. un conjunto de partículas magnetodieléctricas con valores de relativa permitibilidad y permeabilidad mucho mayor que uno y cercano uno al otro;
2. dos partículas dieléctricas diferentes con igual permiso pero diferente tamaño;
3. dos partículas dieléctricas diferentes con igual tamaño pero diferente permittividad.

En teoría, las partículas analizadas por la teoría de Mie son comúnmente esféricas pero, en la práctica, las partículas se fabrican generalmente como cubos o cilindros para facilitar la fabricación. Para cumplir con los criterios de homogeneización, que pueden ser declarados en la forma de que la constante de la celosía es mucho menor que la longitud de onda de funcionamiento, la relativa permittividad de las partículas dieléctricas debe ser mucho mayor que 1, por ejemplo. 78(38)}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε r■78()38){displaystyle varepsilon _{text{r}} {38)}78(38)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/644510d7ced6b9f44a8ed2c96ad8217a1a541018" style="vertical-align: -0.838ex; width:11.518ex; height:2.843ex;"/> para lograr una autorización efectiva negativa (permeabilidad).

Tamaño de partículas

La teoría de Mie se aplica a menudo en el análisis de difracción láser para inspeccionar el efecto del tamaño de las partículas. Si bien las primeras computadoras en la década de 1970 solo podían calcular datos de difracción con la aproximación de Fraunhofer más simple, Mie se usa ampliamente desde la década de 1990 y se recomienda oficialmente para partículas por debajo de 50 micrómetros en la norma ISO 13320: 2009.

La teoría de Mie se ha utilizado en la detección de la concentración de aceite en aguas contaminadas.

La dispersión de Mie es el método principal para dimensionar burbujas de aire sonoluminiscentes individuales en agua y es válida para cavidades en materiales, así como partículas en materiales, siempre que el material circundante sea esencialmente no absorbente.

Parasitología

También se ha utilizado para estudiar la estructura de Plasmodium falciparum, una forma particularmente patógena de malaria.

Extensiones

En 1986, P. A. Bobbert y J. Vlieger ampliaron el modelo de Mie para calcular la dispersión de una esfera en un medio homogéneo colocado sobre una superficie plana. Al igual que el modelo de Mie, el modelo extendido se puede aplicar a esferas con un radio cercano a la longitud de onda de la luz incidente. Hay un código C++ que implementa el modelo Bobbert-Vlieger (BV). Los desarrollos recientes están relacionados con la dispersión por elipsoide. Los estudios contemporáneos van a la conocida investigación de Rayleigh.