Dispersión de luz por partículas
La dispersión de luz por partículas es el proceso por el cual partículas pequeñas (por ejemplo, cristales de hielo, polvo, partículas atmosféricas, polvo cósmico y células sanguíneas) dispersan la luz, lo que provoca fenómenos ópticos como el color azul del cielo y halos.
Las ecuaciones de Maxwell son la base de los métodos teóricos y computacionales que describen la dispersión de la luz, pero como las soluciones exactas de las ecuaciones de Maxwell solo se conocen para geometrías de partículas seleccionadas (como las esféricas), la dispersión de la luz por partículas es una rama del electromagnetismo computacional que se ocupa de la dispersión y absorción de la radiación electromagnética por partículas.
En el caso de geometrías para las que se conocen soluciones analíticas (como esferas, conjuntos de esferas, cilindros infinitos), las soluciones se calculan normalmente en términos de series infinitas. En el caso de geometrías más complejas y para partículas no homogéneas, las ecuaciones originales de Maxwell se discretizan y se resuelven. Los efectos de dispersión múltiple de la luz dispersada por partículas se tratan mediante técnicas de transferencia radiativa (consulte, por ejemplo, los códigos de transferencia radiativa atmosférica).
El tamaño relativo de una partícula dispersante se define por su parámetro de tamaño x, que es la relación entre su dimensión característica y su longitud de onda:
Métodos computacionales exactos
Finite-diferencia método de tiempo-dominio
El método FDTD pertenece a la clase general de métodos de modelado numérico diferencial en el dominio del tiempo basados en cuadrículas. Las ecuaciones de Maxwell dependientes del tiempo (en forma diferencial parcial) se discretizan utilizando aproximaciones de diferencia central a las derivadas parciales de espacio y tiempo. Las ecuaciones de diferencia finita resultantes se resuelven en software o hardware de manera gradual: los componentes del vector del campo eléctrico en un volumen de espacio se resuelven en un instante dado en el tiempo; luego, los componentes del vector del campo magnético en el mismo volumen espacial se resuelven en el siguiente instante en el tiempo; y el proceso se repite una y otra vez hasta que se desarrolla por completo el comportamiento del campo electromagnético transitorio o de estado estable deseado.
T-matrix
La técnica también se conoce como método de campo nulo y método de técnica de límite extendido (EBCM). Los elementos de la matriz se obtienen haciendo coincidir las condiciones de límite para las soluciones de las ecuaciones de Maxwell. El campo incidente, transmitido y disperso se expanden en funciones de onda vectoriales esféricas.
aproximaciones computacionales
Mie aproximación
La dispersión de cualquier partícula esférica con un parámetro de tamaño arbitrario se explica mediante la teoría de Mie. La teoría de Mie, también llamada teoría de Lorenz-Mie o teoría de Lorenz-Mie-Debye, es una solución analítica completa de las ecuaciones de Maxwell para la dispersión de la radiación electromagnética por partículas esféricas (Bohren y Huffman, 1998).
Para formas más complejas, como esferas revestidas, multiesferas, esferoides y cilindros infinitos, existen extensiones que expresan la solución en términos de series infinitas. Hay códigos disponibles para estudiar la dispersión de la luz en la aproximación de Mie para esferas, esferas en capas y esferas y cilindros múltiples.
Dipolo discreto aproximación
Existen varias técnicas para calcular la dispersión de la radiación por partículas de forma arbitraria. La aproximación dipolar discreta es una aproximación del objetivo continuo mediante una matriz finita de puntos polarizables. Los puntos adquieren momentos dipolares en respuesta al campo eléctrico local. Los dipolos de estos puntos interactúan entre sí a través de sus campos eléctricos. Existen códigos DDA disponibles para calcular las propiedades de dispersión de la luz en la aproximación DDA.
Métodos aproximados
| Aproximación | Índice de referencia | Parámetro de tamaño | Cambio de fase |
|---|---|---|---|
| Rayleigh dispersando | abs(mx) muy pequeño | muy pequeño | |
| Óptica geométrica | muy grande | muy grande | |
| Difracción anómala Teoría | abs(m-1) muy pequeño | x grande | |
| Momento angular complejo | m | grande x |
Rayleigh dispersando
El régimen de dispersión de Rayleigh es la dispersión de la luz, u otra radiación electromagnética, por partículas mucho más pequeñas que la longitud de onda de la luz. La dispersión de Rayleigh se puede definir como dispersión en el régimen del parámetro de tamaño pequeño .
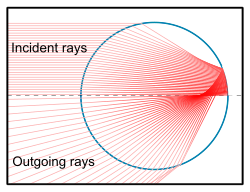
Óptica geométrica (trazado de rayos)
Las técnicas de trazado de rayos pueden aproximarse a la dispersión de la luz no sólo por partículas esféricas, sino también por partículas de cualquier forma (y orientación) especificada, siempre que el tamaño y las dimensiones críticas de una partícula sean mucho mayores que la longitud de onda de la luz. La luz puede considerarse como una colección de rayos cuyos anchos son mucho mayores que la longitud de onda, pero pequeños en comparación con la partícula misma. Cada rayo que incide en la partícula puede sufrir una reflexión y/o refracción (parcial). Estos rayos salen en direcciones así calculadas con su potencia total o (cuando se trata de una reflexión parcial) con la potencia incidente dividida entre dos (o más) rayos salientes. Al igual que con las lentes y otros componentes ópticos, el trazado de rayos determina la luz que emana de un único dispersor y, combinando ese resultado estadísticamente para una gran cantidad de dispersores orientados y posicionados aleatoriamente, se pueden describir fenómenos ópticos atmosféricos como arcoíris debidos a gotas de agua y halos debidos a cristales de hielo. Hay códigos de trazado de rayos de óptica atmosférica disponibles.
Véase también
- Códigos para la dispersión electromagnética por esferas
- Códigos para la dispersión electromagnética por cilindros
- Discreta códigos de aproximación dipole
- Finite-diferencia método de tiempo-dominio
- Scattering
Referencias
- Barber, P.W. y S.C. Hill, Dispersión de luz por partículas: métodos computacionales, Singapur; Teaneck, N.J., World Scientific, c1990, 261 p. + 2 discos computacionales (31⁄2 in.), ISBN 9971-5-0813-3, ISBN 9971-5-0832-X (pbk.)
- Bohren, Craig F. y Donald R. Huffman, Título Absorción y dispersión de la luz por partículas pequeñas, Nueva York: Wiley, 1998, 530 p., ISBN 0-471-29340-7, ISBN 978-0-471-29340-8
- Hulst, H. C. van de, Light scattering by small particles, New York, Dover Publications, 1981, 470 p., ISBN 0-486-64228-3.
- Kerker, Milton, La dispersión de la luz, y otra radiación electromagnética, Nueva York, Académica Press, 1969, 666 p.
- Mishchenko, Michael I., Joop W. Hovenier, Larry D. Travis, Light scattering by nonspherical parts: theory, measurements, and applications, San Diego: Academic Press, 2000, 690 p., ISBN 0-12-498660-9.
- Stratton, Julius Adams, teoría electromagnética, Nueva York, Londres, McGraw-Hill book company, inc., 1941. 615 p.

