Dipolo magnético

El Campo magnético debido a dipoles magnéticos naturales (a la izquierda), monopolios magnéticos (a la derecha), una corriente eléctrica en un bucle circular (a la izquierda) o en un solenoide (a la derecha inferior). Todos generan el mismo perfil de campo cuando el arreglo es infinitamente pequeño.

En electromagnetismo, un dipolo magnético es el límite de un circuito cerrado de corriente eléctrica o de un par de polos cuando el tamaño de la fuente se reduce a cero mientras se mantiene constante el momento magnético. Es un análogo magnético del dipolo eléctrico, pero la analogía no es perfecta. En particular, nunca se ha observado en la naturaleza un verdadero monopolo magnético, el análogo magnético de una carga eléctrica. Sin embargo, se han observado cuasipartículas monopolares magnéticas como propiedades emergentes de ciertos sistemas de materia condensada. Además, una forma de momento dipolar magnético está asociada con una propiedad cuántica fundamental: el giro de las partículas elementales.

Debido a que no existen monopolos magnéticos, el campo magnético a una gran distancia de cualquier fuente magnética estática parece el campo de un dipolo con el mismo momento dipolar. Para fuentes de orden superior (por ejemplo, cuadrupolos) sin momento dipolar, su campo decae hacia cero con la distancia más rápido que un campo dipolar.

Campo magnético externo producido por un momento dipolar magnético

Un análogo electrostático para un momento magnético: dos cargos opuestos separados por una distancia finita. Cada flecha representa la dirección del vector de campo en ese punto.

El campo magnético de un bucle corriente. El anillo representa el bucle actual, que entra en la página en el x y sale en el punto.

En la física clásica, el campo magnético de un dipolo se calcula como el límite de un bucle de corriente o de un par de cargas cuando la fuente se reduce a un punto mientras se mantiene el momento magnético m constante. Para el lazo de corriente, este límite se deriva más fácilmente del vector potencial:

A()r)=μ μ 04π π r2m× × rr=μ μ 04π π m× × rr3,{fnMitbf {f} {fnMitbf}}={fc {fnh}}{4pi} {fnK} {fnMitbf} {fnMitbf} }times {mathbf {r} {fnK} {fnMicroc {fnK} {fnMicrosoft Sans Serif} {fnK} {f}} {fn}} {fn}}} {fn}}} {fn}} {f}}} {fn}}} {fnfnf}} {fnf}f}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfn}fn}fnfn}fnfnfnfnh}\fnfn ¿Qué? }times {mathbf {r} } {r^{3}}}}

donde μ₀ es la constante de permeabilidad al vacío y 4π r² es la superficie de una esfera de radio r. La densidad de flujo magnético (fuerza del campo B) es entonces

B()r)=Silencio Silencio × × A=μ μ 04π π [3r()m⋅ ⋅ r)r5− − mr3].{displaystyle mathbf {B} ({mathbf {r})=nabla times {mathbf {}={frac {m}{4pi}}left[{frac {3mathbf {r} (mathbf {m} cdot mathbf {r}} {r}} {cccc}} {f}}-{f}f} Está bien.

Alternativamente, se puede obtener primero el potencial escalar del límite del polo magnético,

↑ ↑ ()r)=m⋅ ⋅ r4π π r3,{displaystyle psi ({mathbf {r})={frac {mathbf {m} }cdot {mathbf {} {4pi r^{3}}}}

y, por lo tanto, la intensidad del campo magnético (o la intensidad del campo H) es

H()r)=− − Silencio Silencio ↑ ↑ =14π π [3r^ ^ ()m⋅ ⋅ r^ ^ )− − mr3]=Bμ μ 0.{displaystyle {mathbf {H}({mathbf {r})=-nabla psi ={frac {1}{4pi}}left[{frac] {3fnK} (mathbf {m} cdot mathbf {hat {r})-mathbf {m} {}{r^{3}}}}}right]={frac {mathbf {B}{m} {m} {m} {m} {m} {m} {m} {m}}}}} {m}}}}}}} {m}}} {m}}}} {m}}}}}}} {m}}}}}}}}}} {m}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}} {m} {m}}}}}}}}}}}}}}}}}}m}}}}}}}}}}}}}}m}}}}}}}}}}}}}}}}}}}}}}}}}}} - Sí.

La fuerza de campo magnético es simétrica bajo rotaciones sobre el eje del momento magnético. En coordenadas esféricas, con z^ ^ =r^ ^ #⁡ ⁡ Silencio Silencio − − Silencio Silencio ^ ^ pecado⁡ ⁡ Silencio Silencio {displaystyle mathbf {hat {z} # Mathbf {hat {r} cos theta - {boldsymbol {hat {theta }sin theta }, y con el momento magnético alineado con el eje z, entonces la fuerza de campo puede expresarse más simplemente como

H()r)=SilenciomSilencio4π π r3()2#⁡ ⁡ Silencio Silencio r^ ^ +pecado⁡ ⁡ Silencio Silencio Silencio Silencio ^ ^ ).{displaystyle mathbf {H} ({mathbf {r})={frac {mathbf {m} - ¿Qué? +sin theta ,{boldsymbol {hat {theta }}right). }

Campo magnético interno de un dipolo

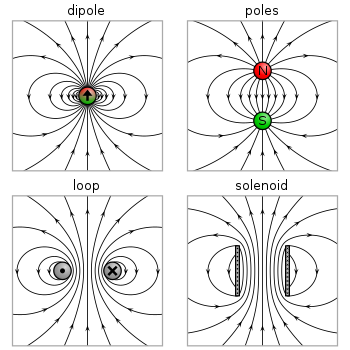
Los dos modelos para un dipolo (bucle de corriente y polos magnéticos) dan las mismas predicciones para el campo magnético lejos de la fuente. Sin embargo, dentro de la región de origen dan predicciones diferentes. El campo magnético entre polos está en dirección opuesta al momento magnético (que apunta de la carga negativa a la carga positiva), mientras que dentro de un bucle de corriente está en la misma dirección (ver la figura a la derecha). Claramente, los límites de estos campos también deben ser diferentes ya que las fuentes se reducen a un tamaño cero. Esta distinción solo importa si el límite del dipolo se usa para calcular campos dentro de un material magnético.

Si se forma un dipolo magnético al hacer un bucle de corriente cada vez más pequeño, pero manteniendo constante el producto de la corriente y el área, el campo límite es

B()r)=μ μ 04π π [3r^ ^ ()r^ ^ ⋅ ⋅ m)− − mSilenciorSilencio3+8π π 3mδ δ ()r)],{displaystyle mathbf {B}mathbf {r}={frac {mu _{0}{4pi}}}left[{frac {3mathbf {hat {hat {r}} {f}} {f}}}m}}}m}}m}m} {f}}}} {f}}}}}}} {f}f} {f}f}f}}}}}}}}}f}f}}}}}f}}f}f}f}}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}}f}fn (mathbf {hat {r} cdot mathbf {m})-mathbf {m} Oh, Dios mío. "Mathbf {m} delta (mathbf {r})right],}

donde δ(r) es la función delta de Dirac en tres dimensiones. A diferencia de las expresiones del apartado anterior, este límite es correcto para el campo interno del dipolo.

Si se forma un dipolo magnético tomando un "polo norte" y un 'polo sur', acercándolos más y más pero manteniendo constante el producto de la carga del polo magnético y la distancia, el campo limitante es

H()r)=14π π [3r^ ^ ()r^ ^ ⋅ ⋅ m)− − mSilenciorSilencio3− − 4π π 3mδ δ ()r)].{displaystyle mathbf {H} {f} {fnMitbf}}left[{frac] {3fnK} (mathbf {hat {r} cdot mathbf {m})-mathbf {m} Oh, Dios mío. } {3}mathbf {m} delta (mathbf {r})right].}

Estos campos están relacionados por B = μ₀(H + M), donde

M()r)=mδ δ ()r){displaystyle mathbf {M} (mathbf {r})=mathbf {m} delta (mathbf {r})}

es la magnetización.

Fuerzas entre dos dipolos magnéticos

La fuerza F ejercida por un momento dipolar m₁ sobre otro m₂ separados en el espacio por un vector r se puede calcular usando:

F=Silencio Silencio ()m2⋅ ⋅ B1),{displaystyle mathbf {F} =nabla left(mathbf {m} _{2}cdot mathbf {B} _{1}derecha),}

o

F()r,m1,m2)=3μ μ 04π π r5[()m1⋅ ⋅ r)m2+()m2⋅ ⋅ r)m1+()m1⋅ ⋅ m2)r− − 5()m1⋅ ⋅ r)()m2⋅ ⋅ r)r2r],{f} {f} {f} {f}} {f}}} {f}} {f}} {f}} {f}} {f} {f}f} {f} {f} {f}f} {f}f} {f}f} {f}f}f}f} {f}f}}f}}}}}}f}f} {f}f}f} {f}}}c}f}}}c}c}c}c}cH00}f}f}c}f}f}c}f} {c}}c}c}c}c}cH00}c}cH00}cH00}c}c}cH00}c}cH00}c}cH00}c}c}c}c}c - {dfrac {5(mathbf {m} _{1}cdot mathbf {r}(mathbf) {m} _{2}cdot mathbf {r} {r^{2}mathbf {r} right],}

donde r es la distancia entre dipolos. La fuerza que actúa sobre m₁ tiene la dirección opuesta.

El par se puede obtener a partir de la fórmula

τ τ =m2× × B1.{displaystyle {boldsymbol {tau }=mathbf {m} _{2}times mathbf {B} _{1}.}

Campos dipolares de fuentes finitas

El potencial escalar magnético ψ producido por una fuente finita, pero externa a ella, puede representarse mediante una expansión multipolar. Cada término en la expansión está asociado con un momento característico y un potencial que tiene una tasa característica de disminución con la distancia r desde la fuente. Los momentos monopolares tienen una tasa de disminución 1/r, los momentos dipolares tienen una 1/r², los momentos cuadripolares tienen un 1/r³ tasa, y así sucesivamente. Cuanto mayor sea el orden, más rápido caerá el potencial. Dado que el término de orden más bajo observado en fuentes magnéticas es el término dipolar, domina a grandes distancias. Por tanto, a grandes distancias cualquier fuente magnética parece un dipolo del mismo momento magnético.