Dinámica molecular

Ejemplo de una simulación de dinámica molecular en un sistema simple: deposición de un átomo de cobre (Cu) en un cristal frío de cobre (Miller index (001) superficie). Cada círculo representa la posición de un átomo. La energía cinética del átomo que se acerca desde la parte superior se redistribuye entre los otros átomos, por lo que en lugar de rebotar sigue unida debido a fuerzas atractivas entre los átomos.

Las simulaciones de dinámica molecular se utilizan a menudo para estudiar sistemas biofísicos. Depicted here is a 100 ps simulation of water.

Una descripción simplificada del algoritmo de simulación de dinámica molecular estándar, cuando se utiliza un integrador tipo predictor-corrector. Las fuerzas pueden provenir de potenciales interatómicos clásicos (descritos matemáticamente como F=− − Silencio Silencio V()r→ → ){displaystyle F=-nabla V({vec {r}}}}) o mecánica cuántica (descrito matemáticamente como F=F()Ψ Ψ ()r→ → )){displaystyle F=F(Psi ({vec {r})})}) métodos. Existen grandes diferencias entre diferentes integradores; algunos no tienen exactamente los mismos términos de orden más alto que se indican en el diagrama de flujo, muchos también utilizan derivados de tiempo de mayor orden, y algunos utilizan tanto el paso actual como el paso del tiempo anterior en los esquemas de paso de tiempo variable.

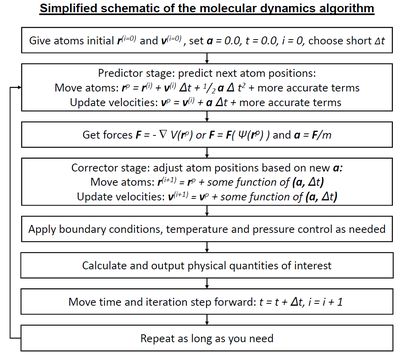
La dinámica molecular (MD) es un método de simulación por computadora para analizar los movimientos físicos de átomos y moléculas. Se permite que los átomos y las moléculas interactúen durante un período fijo de tiempo, dando una visión de la "evolución&#34 dinámica; del sistema. En la versión más común, las trayectorias de átomos y moléculas se determinan resolviendo numéricamente las ecuaciones de movimiento de Newton para un sistema de partículas que interactúan, donde las fuerzas entre las partículas y sus energías potenciales a menudo se calculan utilizando potenciales interatómicos o mecánica molecular. campos de fuerza. El método se aplica principalmente en física química, ciencia de materiales y biofísica.

Debido a que los sistemas moleculares generalmente consisten en una gran cantidad de partículas, es imposible determinar analíticamente las propiedades de tales sistemas complejos; La simulación MD evita este problema utilizando métodos numéricos. Sin embargo, las simulaciones MD largas están mal condicionadas matemáticamente y generan errores acumulativos en la integración numérica que pueden minimizarse con la selección adecuada de algoritmos y parámetros, pero no eliminarse.

Para los sistemas que obedecen a la hipótesis ergódica, se puede usar la evolución de una simulación de dinámica molecular para determinar las propiedades termodinámicas macroscópicas del sistema: los promedios de tiempo de un sistema ergódico corresponden a promedios de conjuntos microcanónicos. MD también se ha denominado "mecánica estadística por números" y la 'visión de Laplace de la mecánica newtoniana' de predecir el futuro animando las fuerzas de la naturaleza y permitiendo comprender el movimiento molecular a escala atómica.

Historia

MD se desarrolló originalmente a principios de la década de 1950, siguiendo los éxitos anteriores con las simulaciones de Monte Carlo, que datan del siglo XVIII, en el problema de la aguja de Buffon, por ejemplo, pero se popularizó para la mecánica estadística en Los Laboratorio Nacional Alamos de Rosenbluth y Metropolis en lo que hoy se conoce como algoritmo Metropolis-Hastings. El interés en la evolución temporal de los sistemas de N-cuerpos data mucho antes del siglo XVII, comenzando con Newton, y continuó en el siglo siguiente en gran parte con un enfoque en la mecánica celeste y cuestiones como la estabilidad del sistema solar. Muchos de los métodos numéricos que se utilizan hoy en día se desarrollaron durante este período de tiempo, anterior al uso de las computadoras; por ejemplo, el algoritmo de integración más común utilizado hoy en día, el algoritmo de integración de Verlet, fue utilizado ya en 1791 por Jean Baptiste Joseph Delambre. Los cálculos numéricos con estos algoritmos se pueden considerar MD "a mano".

Ya en 1941, la integración de las ecuaciones de movimiento de muchos cuerpos se llevó a cabo con computadoras analógicas. Algunos emprendieron el trabajo laborioso de modelar el movimiento atómico mediante la construcción de modelos físicos, por ejemplo, utilizando esferas macroscópicas. El objetivo era disponerlos de tal manera que replicaran la estructura de un líquido y usar esto para examinar su comportamiento. J.D. Bernal dijo, en 1962: "... Tomé varias pelotas de goma y las uní con varillas de una selección de diferentes longitudes que van desde 2,75 a 4 pulgadas. En primer lugar, traté de hacer esto de la manera más casual posible, trabajando en mi propia oficina, interrumpiéndome cada cinco minutos y sin recordar lo que había hecho antes de la interrupción."

Tras el descubrimiento de las partículas microscópicas y el desarrollo de las computadoras, el interés se expandió más allá del campo de pruebas de los sistemas gravitacionales hacia las propiedades estadísticas de la materia. En un intento por comprender el origen de la irreversibilidad, Fermi propuso en 1953 y publicó en 1955 el uso de MANIAC I, también en el Laboratorio Nacional de Los Álamos, para resolver la evolución temporal de las ecuaciones de movimiento para un sistema de muchos cuerpos. a varias elecciones de leyes de fuerza; hoy, este trabajo seminal se conoce como el problema de Fermi-Pasta-Ulam-Tsingou. La evolución temporal de la energía del trabajo original se muestra en la figura de la derecha.

Una de las primeras simulaciones de un sistema N-body fue llevada a cabo en el MANIAC-I por Fermi y compañeros de trabajo para entender los orígenes de la irreversibilidad en la naturaleza. Se muestra aquí la energía versus el tiempo para un sistema de 64 partículas.

En 1957, Alder y Wainwright utilizaron una computadora IBM 704 para simular colisiones perfectamente elásticas entre esferas duras. En 1960, quizás en la primera simulación realista de la materia, Gibson et al. daño por radiación simulado del cobre sólido mediante el uso de un tipo de interacción repulsiva de Born-Mayer junto con una fuerza de superficie cohesiva. En 1964, Rahman publicó simulaciones de argón líquido que usaban un potencial de Lennard-Jones; cálculos de las propiedades del sistema, como el coeficiente de autodifusión, en comparación con los datos experimentales. Hoy en día, el potencial de Lennard-Jones sigue siendo uno de los potenciales intermoleculares más utilizados: se utiliza para describir sustancias simples (también conocidas como Lennard-Jonesio) para estudios conceptuales y de modelos y como componente básico en muchos campos de fuerza de sustancias reales.

Áreas de aplicación y límites

Usado por primera vez en física teórica, el método MD ganó popularidad en la ciencia de materiales poco después y, desde la década de 1970, también es común en bioquímica y biofísica. MD se utiliza con frecuencia para refinar estructuras tridimensionales de proteínas y otras macromoléculas en función de las limitaciones experimentales de la cristalografía de rayos X o la espectroscopia de RMN. En física, MD se utiliza para examinar la dinámica de los fenómenos a nivel atómico que no se pueden observar directamente, como el crecimiento de películas delgadas y la subplantación de iones, y también para examinar las propiedades físicas de los dispositivos nanotecnológicos que no se han creado o aún no se pueden crear.. En biofísica y biología estructural, el método se aplica con frecuencia para estudiar los movimientos de macromoléculas como proteínas y ácidos nucleicos, que pueden ser útiles para interpretar los resultados de ciertos experimentos biofísicos y para modelar interacciones con otras moléculas, como en el acoplamiento de ligandos. En principio, la MD se puede utilizar para la predicción ab initio de la estructura de la proteína mediante la simulación del plegamiento de la cadena polipeptídica a partir de una espiral aleatoria.

Los resultados de las simulaciones MD se pueden probar comparándolos con experimentos que miden la dinámica molecular, de los cuales un método popular es la espectroscopia de RMN. Las predicciones de estructura derivadas de MD se pueden probar a través de experimentos en toda la comunidad en Evaluación crítica de predicción de estructura de proteína (CASP), aunque históricamente el método ha tenido un éxito limitado en esta área. Michael Levitt, quien compartió el Premio Nobel en parte por la aplicación de MD a las proteínas, escribió en 1999 que los participantes del CASP generalmente no usaban el método debido a "... una vergüenza central de la mecánica molecular, a saber, que la minimización de energía o la dinámica molecular generalmente conducen a un modelo que se parece menos a la estructura experimental." Las mejoras en los recursos computacionales que permiten más y más largas trayectorias MD, combinadas con las mejoras modernas en la calidad de los parámetros del campo de fuerza, han producido algunas mejoras tanto en la predicción de estructuras como en el refinamiento del modelo de homología, sin alcanzar el punto de utilidad práctica en estas áreas; muchos identifican los parámetros del campo de fuerza como un área clave para un mayor desarrollo.

Se ha informado sobre la simulación MD para el desarrollo de farmacóforos y el diseño de fármacos. Por ejemplo, Pinto et al. implementó simulaciones MD de complejos Bcl-Xl para calcular las posiciones promedio de los aminoácidos críticos involucrados en la unión del ligando. Por otro lado, Carlson et al. implementó simulación de dinámica molecular para identificar compuestos que complementan al receptor mientras causan una interrupción mínima de la conformación y flexibilidad del sitio activo. Se superpusieron instantáneas de la proteína a intervalos de tiempo constantes durante la simulación para identificar regiones de unión conservadas (conservadas en al menos tres de once fotogramas) para el desarrollo de farmacóforos. Spyrakis et al. se basó en un flujo de trabajo de simulaciones MD, huellas dactilares para ligandos y proteínas (FLAP) y análisis de discriminación lineal para identificar las mejores conformaciones ligando-proteína para actuar como plantillas de farmacóforo basadas en análisis ROC retrospectivo de los farmacóforos resultantes. En un intento por mejorar el modelado de descubrimiento de fármacos basado en la estructura, frente a la necesidad de muchos compuestos modelados, Hatmal et al. propuso una combinación de simulación MD y análisis de contactos intermoleculares ligando-receptor para distinguir los contactos intermoleculares críticos (interacciones de unión) de los redundantes en un solo complejo ligando-proteína. Luego, los contactos críticos se pueden convertir en modelos de farmacóforos que se pueden usar para la detección virtual.

Los límites del método están relacionados con los conjuntos de parámetros utilizados y con los campos de fuerza subyacentes de la mecánica molecular. Una ejecución de una simulación MD optimiza la energía potencial, en lugar de la energía libre de la proteína, lo que significa que se descuidan todas las contribuciones entrópicas a la estabilidad termodinámica de la estructura de la proteína, incluida la entropía conformacional de la cadena polipeptídica (el factor principal que desestabiliza la estructura de la proteína).) y efectos hidrofóbicos (las principales fuerzas impulsoras del plegamiento de proteínas). Otro factor importante son los enlaces de hidrógeno intramoleculares, que no se incluyen explícitamente en los campos de fuerza modernos, pero se describen como interacciones de Coulomb de cargas puntuales atómicas. Esta es una aproximación cruda porque los enlaces de hidrógeno tienen una naturaleza mecánica y química parcialmente cuántica. Además, las interacciones electrostáticas generalmente se calculan utilizando la constante dieléctrica del vacío, aunque la solución acuosa circundante tiene una constante dieléctrica mucho más alta. El uso de la constante dieléctrica macroscópica a distancias interatómicas cortas es cuestionable. Finalmente, las interacciones de van der Waals en MD generalmente se describen mediante potenciales de Lennard-Jones basados en la teoría de Fritz London que solo es aplicable en el vacío. Sin embargo, todos los tipos de fuerzas de van der Waals son, en última instancia, de origen electrostático y, por lo tanto, dependen de las propiedades dieléctricas del entorno. La medición directa de las fuerzas de atracción entre diferentes materiales (como la constante de Hamaker) muestra que "la interacción entre los hidrocarburos en el agua es aproximadamente el 10 % de la interacción en el vacío". La dependencia del entorno de las fuerzas de van der Waals se desprecia en las simulaciones estándar, pero se puede incluir desarrollando campos de fuerza polarizables.

Restricciones de diseño

El diseño de una simulación de dinámica molecular debe tener en cuenta la potencia computacional disponible. El tamaño de la simulación (n = número de partículas), el intervalo de tiempo y la duración total del tiempo deben seleccionarse para que el cálculo pueda finalizar en un período de tiempo razonable. Sin embargo, las simulaciones deben ser lo suficientemente largas para ser relevantes para las escalas de tiempo de los procesos naturales que se estudian. Para sacar conclusiones estadísticamente válidas de las simulaciones, el lapso de tiempo simulado debe coincidir con la cinética del proceso natural. De lo contrario, es análogo a sacar conclusiones sobre cómo camina un ser humano cuando solo mira menos de un paso. La mayoría de las publicaciones científicas sobre la dinámica de las proteínas y el ADN utilizan datos de simulaciones que van desde nanosegundos (10⁻⁹ s) hasta microsegundos (10⁻⁶ s). Para obtener estas simulaciones, se necesitan varios días de CPU a años de CPU. Los algoritmos paralelos permiten distribuir la carga entre las CPU; un ejemplo es el algoritmo de descomposición espacial o de fuerzas.

Durante una simulación clásica de MD, la tarea más intensa de la CPU es la evaluación del potencial como función de las coordenadas internas de las partículas. Dentro de esa evaluación energética, la más cara es la parte no abonada o no covalente. En Big O notation, simulaciones de dinámica molecular común escala por O()n2){displaystyle O(n^{2}} si todas las interacciones electrostáticas y van der Waals en pareja deben ser contabilizadas explícitamente. Este costo computacional puede reducirse empleando métodos electrostáticos como la malla de partículas Summación de Ewald (en inglés)O()nlog⁡ ⁡ ()n)){displaystyle O(nlog(n)}), partícula-partícula-partícula-mesh (P3M), o buenos métodos de corte esférico (O()n){displaystyle O(n)}).

Otro factor que afecta el tiempo total de CPU que necesita una simulación es el tamaño del paso de tiempo de integración. Este es el período de tiempo entre las evaluaciones del potencial. El paso de tiempo debe elegirse lo suficientemente pequeño para evitar errores de discretización (es decir, más pequeño que el período relacionado con la frecuencia vibratoria más rápida del sistema). Los intervalos de tiempo típicos para MD clásica son del orden de 1 femtosegundo (10⁻¹⁵ s). Este valor se puede ampliar mediante el uso de algoritmos como el algoritmo de restricción SHAKE, que fija las vibraciones de los átomos más rápidos (por ejemplo, los hidrógenos) en su lugar. También se han desarrollado métodos de escala de tiempo múltiple, que permiten tiempos prolongados entre actualizaciones de fuerzas de largo alcance más lentas.

Para simular moléculas en un solvente, se debe elegir entre solvente explícito e implícito. Las partículas de disolventes explícitas (como los modelos de agua TIP3P, SPC/E y SPC-f) deben calcularse de forma costosa mediante el campo de fuerza, mientras que los disolventes implícitos utilizan un enfoque de campo medio. El uso de un solvente explícito es computacionalmente costoso y requiere la inclusión de aproximadamente diez veces más partículas en la simulación. Pero la granularidad y la viscosidad del solvente explícito son esenciales para reproducir ciertas propiedades de las moléculas del soluto. Esto es especialmente importante para reproducir la cinética química.

En todos los tipos de simulaciones de dinámica molecular, el tamaño del cuadro de simulación debe ser lo suficientemente grande para evitar artefactos de condiciones límite. Las condiciones de contorno a menudo se tratan eligiendo valores fijos en los bordes (que pueden causar artefactos) o empleando condiciones de contorno periódicas en las que un lado de la simulación vuelve al lado opuesto, imitando una fase masiva (que también puede causar artefactos)..

Representación esquemática del muestreo de la superficie energética potencial del sistema con dinámica molecular (en rojo) en comparación con los métodos Monte Carlo (en azul).

Conjunto microcanónico (NVE)

En el conjunto microcanónico, el sistema está aislado de cambios en los moles (N), volumen (V) y energía (E). Corresponde a un proceso adiabático sin cambio de calor. Una trayectoria de dinámica molecular microcanónica puede considerarse como un intercambio de energía potencial y cinética, con una energía total conservada. Para un sistema de partículas N con coordenadas X{displaystyle X} y velocidades V{displaystyle V}, el siguiente par de ecuaciones diferenciales de primer orden se puede escribir en la notación de Newton como

F()X)=− − Silencio Silencio U()X)=MVÍ Í ()t){displaystyle F(X)=-nabla U(X)=M{dot {V}(t)}

V()t)=XÍ Í ()t).{displaystyle V(t)={dot {X}(t).}

La función energética potencial U()X){displaystyle U(X)} del sistema es una función de las coordenadas de partículas X{displaystyle X}. Se refiere simplemente como el potencial en física, o sobre el terreno en química. La primera ecuación proviene de las leyes de movimiento de Newton; la fuerza F{displaystyle F} actuar en cada partícula del sistema se puede calcular como el gradiente negativo de U()X){displaystyle U(X)}.

Por cada paso del tiempo, la posición de cada partícula X{displaystyle X} y velocidad V{displaystyle V} puede integrarse con un método integrador simpático como la integración Verlet. La evolución del tiempo X{displaystyle X} y V{displaystyle V} se llama trayectoria. Dada la posición inicial (por ejemplo, del conocimiento teórico) y las velocidades (por ejemplo, Gaussian aleatorizado), podemos calcular todas las posiciones y velocidades futuras (o pasadas).

Una fuente frecuente de confusión es el significado de la temperatura en MD. Comúnmente tenemos experiencia con temperaturas macroscópicas, que involucran una gran cantidad de partículas. Pero la temperatura es una cantidad estadística. Si hay un número suficientemente grande de átomos, la temperatura estadística se puede estimar a partir de la temperatura instantánea, que se encuentra igualando la energía cinética del sistema a nk_BT/2 donde n es el número de grados de libertad del sistema.

Un fenómeno relacionado con la temperatura surge debido al pequeño número de átomos que se utilizan en simulaciones MD. Por ejemplo, considere simular el crecimiento de una película de cobre comenzando con un sustrato que contiene 500 átomos y una energía de deposición de 100 eV. En el mundo real, los 100 eV del átomo depositado serían rápidamente transportados y compartidos entre un gran número de átomos (1010{displaystyle 10^{10} o más) sin grandes cambios en la temperatura. Cuando hay sólo 500 átomos, sin embargo, el sustrato es casi inmediatamente vaporizado por la deposición. Algo similar ocurre en simulaciones biofísicas. La temperatura del sistema en NVE se eleva naturalmente cuando macromoléculas como proteínas experimentan cambios de conformación exotérmica y unión.

Conjunto canónico (NVT)

En el conjunto canónico se conservan la cantidad de sustancia (N), el volumen (V) y la temperatura (T). A veces también se le llama dinámica molecular a temperatura constante (CTMD). En NVT, la energía de los procesos endotérmicos y exotérmicos se intercambia con un termostato.

Hay disponible una variedad de algoritmos de termostato para agregar y quitar energía de los límites de una simulación MD de una manera más o menos realista, acercándose al conjunto canónico. Los métodos populares para controlar la temperatura incluyen el cambio de escala de velocidad, el termostato Nosé-Hoover, las cadenas Nosé-Hoover, el termostato Berendsen, el termostato Andersen y la dinámica de Langevin. El termostato Berendsen podría introducir el efecto de cubo de hielo volador, lo que conduce a traslaciones y rotaciones no físicas del sistema simulado.

No es trivial obtener una distribución de conjuntos canónicos de conformaciones y velocidades utilizando estos algoritmos. La forma en que esto depende del tamaño del sistema, la elección del termostato, los parámetros del termostato, el paso de tiempo y el integrador es el tema de muchos artículos en el campo.

Conjunto isotérmico-isobárico (NPT)

En el conjunto isotérmico-isobárico, se conservan la cantidad de sustancia (N), la presión (P) y la temperatura (T). Además de un termostato, se necesita un barostato. Corresponde más estrechamente a las condiciones de laboratorio con un matraz abierto a temperatura y presión ambiente.

En la simulación de membranas biológicas, el control de presión isotrópica no es apropiado. Para las bicapas lipídicas, el control de la presión se produce bajo un área de membrana constante (NPAT) o una tensión superficial constante "gamma" (NPγT).

Conjuntos generalizados

El método de intercambio de réplicas es un conjunto generalizado. Originalmente fue creado para lidiar con la dinámica lenta de los sistemas de espín desordenados. También se le llama templado paralelo. La formulación MD de intercambio de réplicas (REMD) intenta superar el problema de los mínimos múltiples intercambiando la temperatura de las réplicas del sistema que no interactúan y funcionan a varias temperaturas.

Potenciales en simulaciones MD

Una simulación de dinámica molecular requiere la definición de una función potencial o una descripción de los términos mediante los cuales interactuarán las partículas en la simulación. En química y biología esto se suele denominar campo de fuerza y en física de materiales como potencial interatómico. Los potenciales pueden definirse en muchos niveles de precisión física; los que se utilizan con mayor frecuencia en química se basan en la mecánica molecular y representan un tratamiento mecánico clásico de las interacciones partícula-partícula que puede reproducir cambios estructurales y conformacionales, pero por lo general no puede reproducir reacciones químicas.

La reducción de una descripción totalmente cuántica a un potencial clásico implica dos aproximaciones principales. La primera es la aproximación de Born-Oppenheimer, que establece que la dinámica de los electrones es tan rápida que se puede considerar que reaccionan instantáneamente al movimiento de sus núcleos. En consecuencia, pueden tratarse por separado. El segundo trata a los núcleos, que son mucho más pesados que los electrones, como partículas puntuales que siguen la dinámica newtoniana clásica. En la dinámica molecular clásica, el efecto de los electrones se aproxima como una superficie de energía potencial, que normalmente representa el estado fundamental.

Cuando se necesitan niveles de detalle más finos, se utilizan potenciales basados en la mecánica cuántica; algunos métodos intentan crear potenciales híbridos clásicos/cuánticos en los que la mayor parte del sistema se trata de forma clásica, pero una pequeña región se trata como un sistema cuántico, que normalmente sufre una transformación química.

Potenciales empíricos

Los potenciales empíricos que se utilizan en química se denominan con frecuencia campos de fuerza, mientras que los que se utilizan en física de materiales se denominan potenciales interatómicos.

La mayoría de los campos de fuerza en química son empíricos y consisten en una suma de fuerzas enlazadas asociadas con enlaces químicos, ángulos de enlace y diedros de enlace, y fuerzas no enlazadas asociadas con fuerzas de van der Waals y carga electrostática. Los potenciales empíricos representan efectos mecánico-cuánticos de forma limitada a través de aproximaciones funcionales ad hoc. Estos potenciales contienen parámetros libres como la carga atómica, los parámetros de van der Waals que reflejan estimaciones del radio atómico y la longitud, el ángulo y el diedro del enlace de equilibrio; estos se obtienen comparándolos con cálculos electrónicos detallados (simulaciones químicas cuánticas) o propiedades físicas experimentales, como constantes elásticas, parámetros de red y medidas espectroscópicas.

Debido a la naturaleza no local de las interacciones no enlazadas, implican al menos interacciones débiles entre todas las partículas del sistema. Su cálculo suele ser el cuello de botella en la velocidad de las simulaciones MD. Para reducir el costo computacional, los campos de fuerza emplean aproximaciones numéricas como radios de corte desplazados, algoritmos de campo de reacción, suma de Ewald de malla de partículas o la nueva malla de partículas-partículas-partículas (P3M).

Los campos de fuerza químicos comúnmente emplean arreglos de enlace preestablecidos (una excepción es la dinámica ab initio) y, por lo tanto, no pueden modelar el proceso de ruptura de enlaces químicos y las reacciones explícitamente. Por otro lado, muchos de los potenciales utilizados en física, como los que se basan en el formalismo del orden de los enlaces, pueden describir varias coordinaciones diferentes de un sistema y la ruptura de enlaces. Ejemplos de tales potenciales incluyen el potencial de Brenner para hidrocarburos y su nuevos desarrollos para los sistemas C-Si-H y C-O-H. El potencial ReaxFF puede considerarse un híbrido totalmente reactivo entre los potenciales de orden de enlace y los campos de fuerza químicos.

Potenciales de pares versus potenciales de muchos cuerpos

Las funciones potenciales que representan la energía no ligada se formulan como una suma de las interacciones entre las partículas del sistema. La opción más simple, empleada en muchos campos de fuerza populares, es el 'par potencial', en el que la energía potencial total se puede calcular a partir de la suma de las contribuciones de energía entre pares de átomos. Por lo tanto, estos campos de fuerza también se denominan "campos de fuerza aditivos". Un ejemplo de un potencial de par de este tipo es el potencial de Lennard-Jones no enlazado (también denominado potencial 6-12), que se utiliza para calcular las fuerzas de van der Waals.

U()r)=4ε ε [()σ σ r)12− − ()σ σ r)6]{displaystyle U(r)=4varepsilon left[left({frac {sigma ¿Qué? Bien.

Otro ejemplo es el modelo Born (iónico) de la red iónica. El primer término de la siguiente ecuación es la ley de Coulomb para un par de iones, el segundo término es la repulsión de corto alcance explicada por el principio de exclusión de Pauli y el término final es el término de interacción de dispersión. Por lo general, una simulación solo incluye el término dipolar, aunque a veces también se incluye el término cuadrupolar. Cuando n_l = 6, este potencial también se denomina potencial de Coulomb-Buckingham.

Uij()rij)=zizj4π π ε ε 01rij+Alexp⁡ ⁡ − − rijpl+Clrij− − nl+⋯ ⋯ {displaystyle U_{ij}(r_{ij})={frac {Z_{i}z_{j}{4pi} "Epsilon" {1} {fn}}fn}fnK}}fnK}}} {fnMicroc {-r_{} {cdots}}cdots}

En los potenciales de muchos cuerpos, la energía potencial incluye los efectos de tres o más partículas que interactúan entre sí. En simulaciones con potenciales por pares, también existen interacciones globales en el sistema, pero ocurren solo a través de términos por pares. En los potenciales de muchos cuerpos, la energía potencial no se puede encontrar mediante una suma de pares de átomos, ya que estas interacciones se calculan explícitamente como una combinación de términos de orden superior. Desde el punto de vista estadístico, la dependencia entre las variables en general no puede expresarse usando solo productos por pares de los grados de libertad. Por ejemplo, el potencial de Tersoff, que se usó originalmente para simular el carbono, el silicio y el germanio, y desde entonces se ha usado para una amplia gama de otros materiales, involucra una suma sobre grupos de tres átomos, siendo los ángulos entre los átomos un factor importante en el potencial. Otros ejemplos son el método del átomo incrustado (EAM), el EDIP y los potenciales de aproximación del segundo momento de unión estrecha (TBSMA), donde la densidad electrónica de los estados en la región de un átomo se calcula a partir de la suma de las contribuciones de los átomos circundantes., y la contribución de energía potencial es entonces una función de esta suma.

Potenciales semiempíricos

Los potenciales semiempíricos hacen uso de la representación matricial de la mecánica cuántica. Sin embargo, los valores de los elementos de la matriz se encuentran mediante fórmulas empíricas que estiman el grado de superposición de orbitales atómicos específicos. Luego, la matriz se diagonaliza para determinar la ocupación de los diferentes orbitales atómicos, y las fórmulas empíricas se usan una vez más para determinar las contribuciones de energía de los orbitales.

Existe una amplia variedad de potenciales semiempíricos, denominados potenciales de enlace estrecho, que varían según los átomos que se modelen.

Potenciales polarizables

La mayoría de los campos de fuerza clásicos incluyen implícitamente el efecto de la polarizabilidad, por ejemplo, aumentando las cargas parciales obtenidas de los cálculos químicos cuánticos. Estas cargas parciales son estacionarias con respecto a la masa del átomo. Pero las simulaciones de dinámica molecular pueden modelar explícitamente la polarizabilidad con la introducción de dipolos inducidos a través de diferentes métodos, como partículas Drude o cargas fluctuantes. Esto permite una redistribución dinámica de la carga entre los átomos que responde al entorno químico local.

Durante muchos años, las simulaciones MD polarizables se han promocionado como la próxima generación. Para líquidos homogéneos como el agua, se ha logrado una mayor precisión mediante la inclusión de la polarizabilidad. También se han logrado algunos resultados prometedores para las proteínas. Sin embargo, todavía no está claro cómo aproximar mejor la polarizabilidad en una simulación. El punto se vuelve más importante cuando una partícula experimenta diferentes entornos durante su trayectoria de simulación, p. translocación de un fármaco a través de una membrana celular.

Potencialidades en métodos ab initio

En la dinámica molecular clásica, una superficie de energía potencial (generalmente el estado fundamental) se representa en el campo de fuerza. Esta es una consecuencia de la aproximación de Born-Oppenheimer. En estados excitados, reacciones químicas o cuando se necesita una representación más precisa, el comportamiento electrónico se puede obtener a partir de primeros principios utilizando un método de mecánica cuántica, como la teoría funcional de la densidad. Esto se llama Ab Initio Molecular Dynamics (AIMD). Debido al costo de tratar los grados de libertad electrónicos, la carga computacional de estas simulaciones es mucho mayor que la dinámica molecular clásica. Por esta razón, AIMD generalmente se limita a sistemas más pequeños y tiempos más cortos.

Ab initio Los métodos mecánicos y químicos cuánticos pueden usarse para calcular la energía potencial de un sistema sobre la marcha, según sea necesario para conformaciones en una trayectoria. Este cálculo generalmente se realiza en la vecindad cercana de la coordenada de reacción. Aunque se pueden usar varias aproximaciones, estas se basan en consideraciones teóricas, no en un ajuste empírico. Los cálculos ab initio producen una gran cantidad de información que no está disponible a partir de métodos empíricos, como la densidad de estados electrónicos u otras propiedades electrónicas. Una ventaja significativa de usar métodos ab initio es la capacidad de estudiar reacciones que involucran la ruptura o formación de enlaces covalentes, que corresponden a múltiples estados electrónicos. Además, los métodos ab initio también permiten recuperar efectos más allá de la aproximación de Born-Oppenheimer utilizando enfoques como la dinámica clásica cuántica mixta.

Híbrido QM/MM

Los métodos QM (mecánica cuántica) son muy poderosos. Sin embargo, son costosos desde el punto de vista computacional, mientras que los métodos MM (mecánica clásica o molecular) son rápidos pero tienen varios límites (requieren una parametrización extensa; las estimaciones de energía obtenidas no son muy precisas; no se pueden usar para simular reacciones donde se rompen/forman enlaces covalentes). y están limitados en sus capacidades para proporcionar detalles precisos sobre el entorno químico). Ha surgido una nueva clase de método que combina las ventajas de los cálculos QM (precisión) y MM (velocidad). Estos métodos se denominan métodos mixtos o híbridos de mecánica cuántica y mecánica molecular (QM/MM híbrido).

La ventaja más importante del método híbrido QM/MM es la velocidad. El costo de hacer dinámica molecular clásica (MM) en el caso más sencillo escala O(n²), donde n es el número de átomos en el sistema. Esto se debe principalmente al término de interacciones electrostáticas (cada partícula interactúa con todas las demás partículas). Sin embargo, el uso del radio de corte, las actualizaciones periódicas de la lista de pares y, más recientemente, las variaciones del método de malla de partículas de Ewald (PME) han reducido esto a entre O(n) y O(n^{2). En otras palabras, si se simula un sistema con el doble de átomos, se necesitaría entre dos y cuatro veces más potencia de cálculo. Por otro lado, los cálculos ab initio más simples suelen escalar O(n3) o peor (se han sugerido cálculos restringidos de Hartree-Fock para escalar ~O(n2.7)). Para superar el límite, una pequeña parte del sistema se trata mecánicamente cuánticamente (normalmente, el sitio activo de una enzima) y el sistema restante se trata de forma clásica.}

En implementaciones más sofisticadas, existen métodos QM/MM para tratar tanto los núcleos ligeros susceptibles a los efectos cuánticos (como los hidrógenos) como los estados electrónicos. Esto permite generar funciones de onda de hidrógeno (similares a las funciones de onda electrónicas). Esta metodología ha sido útil en la investigación de fenómenos como la formación de túneles de hidrógeno. Un ejemplo en el que los métodos QM/MM han proporcionado nuevos descubrimientos es el cálculo de la transferencia de hidruros en la enzima alcohol deshidrogenasa del hígado. En este caso, la tunelización cuántica es importante para el hidrógeno, ya que determina la velocidad de reacción.

Representaciones granulares y reducidas

En el otro extremo de la escala de detalles se encuentran los modelos de grano grueso y de celosía. En lugar de representar explícitamente cada átomo del sistema, se utilizan "pseudoátomos" para representar grupos de átomos. Las simulaciones MD en sistemas muy grandes pueden requerir recursos informáticos tan grandes que no pueden estudiarse fácilmente con los métodos tradicionales de todos los átomos. De manera similar, las simulaciones de procesos en escalas de tiempo largas (más allá de aproximadamente 1 microsegundo) son prohibitivamente costosas, porque requieren muchos pasos de tiempo. En estos casos, a veces se puede abordar el problema utilizando representaciones reducidas, que también se denominan modelos de grano grueso.

Ejemplos de métodos de grano grueso (CG) son la dinámica molecular discontinua (CG-DMD) y los modelos Go. El granulado grueso se realiza a veces tomando pseudoátomos más grandes. Tales aproximaciones de átomos unidos se han utilizado en simulaciones MD de membranas biológicas. La implementación de este enfoque en sistemas donde las propiedades eléctricas son de interés puede ser un desafío debido a la dificultad de utilizar una distribución de carga adecuada en los pseudoátomos. Las colas alifáticas de los lípidos están representadas por unos pocos pseudoátomos reuniendo de 2 a 4 grupos metileno en cada pseudoátomo.

La parametrización de estos modelos de granularidad muy gruesa debe realizarse empíricamente, haciendo coincidir el comportamiento del modelo con datos experimentales apropiados o simulaciones de todos los átomos. Idealmente, estos parámetros deberían tener en cuenta las contribuciones tanto entálpicas como entrópicas a la energía libre de forma implícita. Cuando la granularidad gruesa se realiza a niveles más altos, la precisión de la descripción dinámica puede ser menos confiable. Pero los modelos de grano muy grueso se han utilizado con éxito para examinar una amplia gama de cuestiones en biología estructural, organización de cristales líquidos y vidrios poliméricos.

Ejemplos de aplicaciones de granulado grueso:

• Los estudios de predicción de la estructura de proteínas y plegables se realizan a menudo utilizando uno, o algunos, pseudo-atomos por aminoácido;
• Se han examinado las transiciones de fases de cristal líquido en geometrías confinadas y/o durante el flujo utilizando el potencial Gay-Berne, que describe especies anisotrópicas;
• Las gafas de polímero durante la deformación han sido estudiadas usando resortes simples armónicos o FENE para conectar las esferas descritas por el potencial Lennard-Jones;
• El supercoiling de ADN se ha investigado utilizando seudónimos de 1 a 3 por base, y en menor resolución;
• Se ha investigado el empaque de ADN de doble ayuda en bacteriófago con modelos en los que un pseudo-atómago representa un giro (alrededor de 10 puntos básicos) del doble helix;
• La estructura del ARN en el ribosoma y otros sistemas grandes se ha modelado con un pseudo-atomo por nucleótido.
• Simulación de células virtuales para estudiar la interacción de células y diversos sustratos.

La forma más simple de granulado grueso es el átomo unido (a veces llamado átomo extendido) y se utilizó en la mayoría de las primeras simulaciones MD de proteínas, lípidos y ácidos nucleicos.. Por ejemplo, en lugar de tratar los cuatro átomos de un grupo metilo CH₃ explícitamente (o los tres átomos del grupo metileno CH₂), uno representa el grupo completo con un pseudo -átomo. Por supuesto, debe parametrizarse correctamente para que sus interacciones de van der Waals con otros grupos tengan la dependencia adecuada de la distancia. Se aplican consideraciones similares a los enlaces, ángulos y torsiones en los que participa el pseudoátomo. En este tipo de representación de átomos unidos, normalmente se eliminan todos los átomos de hidrógeno explícitos excepto aquellos que tienen la capacidad de participar en enlaces de hidrógeno (hidrógenos polares). Un ejemplo de esto es el campo de fuerza CHARMM 19.

Los hidrógenos polares generalmente se conservan en el modelo, porque el tratamiento adecuado de los enlaces de hidrógeno requiere una descripción razonablemente precisa de la direccionalidad y las interacciones electrostáticas entre los grupos donante y aceptor. Un grupo hidroxilo, por ejemplo, puede ser tanto donante de enlaces de hidrógeno como aceptor de enlaces de hidrógeno, y sería imposible tratar esto con un pseudoátomo de OH. Aproximadamente la mitad de los átomos en una proteína o ácido nucleico son hidrógenos no polares, por lo que el uso de átomos unidos puede proporcionar un ahorro sustancial en el tiempo de computación.

Incorporar efectos solventes

En muchas simulaciones de un sistema soluto-solvente, el enfoque principal está en el comportamiento del soluto con poco interés en el comportamiento del solvente, particularmente en aquellas moléculas de solvente que residen en regiones alejadas de la molécula del soluto. Los solventes pueden influir en el comportamiento dinámico de los solutos a través de colisiones aleatorias y al imponer un arrastre por fricción en el movimiento del soluto a través del solvente. El uso de condiciones de contorno periódicas no rectangulares, límites estocásticos y capas de solvente pueden ayudar a reducir la cantidad de moléculas de solvente requeridas y permitir que una mayor proporción del tiempo de cálculo se dedique a simular el soluto. También es posible incorporar los efectos de un disolvente sin necesidad de que esté presente ninguna molécula de disolvente explícita. Un ejemplo de este enfoque es usar una fuerza media potencial (PMF) que describe cómo cambia la energía libre cuando se varía una coordenada particular. El cambio de energía libre descrito por PMF contiene los efectos promedio del solvente.

Sin incorporar los efectos de los solventes, las simulaciones de macromoléculas (como las proteínas) pueden generar un comportamiento poco realista e incluso las moléculas pequeñas pueden adoptar conformaciones más compactas debido a las fuerzas de van der Waals favorables y las interacciones electrostáticas que se atenuarían en presencia de un solvente..

Fuerzas de largo alcance

Una interacción de largo alcance es una interacción en la que la interacción espacial cae no más rápido que r− − d{displaystyle r^{-d} Donde d{displaystyle d} es la dimensionalidad del sistema. Ejemplos incluyen interacciones de carga entre iones y dipole-dipole interacciones entre moléculas. La modelación de estas fuerzas presenta un reto bastante grande ya que son significativos a lo largo de una distancia que puede ser mayor de la mitad de la longitud de la caja con simulaciones de miles de partículas. Aunque una solución sería aumentar significativamente el tamaño de la longitud de la caja, este enfoque de fuerza bruta es menos que ideal ya que la simulación sería computacionalmente muy caro. Spherically truncating the potential is also out of the question as unrealistic behaviour may be observed when the distance is close to the cut off distance.

Dinámica molecular dirigida (SMD)

Las simulaciones de dinámica molecular dirigida (SMD), o simulaciones de sonda de fuerza, aplican fuerzas a una proteína para manipular su estructura tirando de ella a lo largo de los grados de libertad deseados. Estos experimentos se pueden utilizar para revelar cambios estructurales en una proteína a nivel atómico. SMD se usa a menudo para simular eventos como el despliegue mecánico o el estiramiento.

Hay dos protocolos típicos de SMD: uno en el que la velocidad de tracción se mantiene constante y otro en el que la fuerza aplicada es constante. Por lo general, parte del sistema estudiado (p. ej., un átomo en una proteína) está restringido por un potencial armónico. Luego se aplican fuerzas a átomos específicos a una velocidad constante o una fuerza constante. El muestreo paraguas se utiliza para mover el sistema a lo largo de la coordenada de reacción deseada variando, por ejemplo, las fuerzas, las distancias y los ángulos manipulados en la simulación. A través del muestreo general, todas las configuraciones del sistema, tanto de alta como de baja energía, se muestrean adecuadamente. Luego, el cambio de energía libre de cada configuración se puede calcular como el potencial de la fuerza media. Un método popular para calcular PMF es a través del método de análisis de histograma ponderado (WHAM), que analiza una serie de simulaciones de muestreo general.

Muchas aplicaciones importantes de SMD se encuentran en el campo del descubrimiento de fármacos y las ciencias biomoleculares. Por ej. SMD se utilizó para investigar la estabilidad de las protofibrillas de Alzheimer, para estudiar la interacción proteína-ligando en la quinasa 5 dependiente de ciclina e incluso para mostrar el efecto del campo eléctrico en el complejo de trombina (proteína) y aptámero (nucleótido), entre muchos otros. interesantes estudios.

Ejemplos de aplicaciones

Simulación de dinámica molecular de un motor molecular sintético compuesto por tres moléculas en un nanopore (diámetro exterior 6.7 nm) a 250 K.

La dinámica molecular se utiliza en muchos campos de la ciencia.

• En 1975 se publicó la primera simulación MD de un proceso de plegado biológico simplificado. Su simulación publicada en Nature allanó el camino para el vasto área de la proteína computacional moderna.
• En 1976 se publicó la primera simulación MD de un proceso biológico. Su simulación publicada en Nature allanó el camino para entender el movimiento de proteínas como esencial en la función y no sólo accesorio.
• El MD es el método estándar para tratar las cascadas de colisión en el régimen del pico de calor, es decir, los efectos que la irradiación energética de neutrones e iones tienen en sólidos y superficies sólidas.

Los siguientes ejemplos biofísicos ilustran esfuerzos notables para producir simulaciones de sistemas de tamaño muy grande (un virus completo) o tiempos de simulación muy largos (hasta 1.112 milisegundos):

• MD simulation of the full virus del mosaico de tabaco (STMV) (2006, Tamaño: 1 millón de átomos, tiempo de simulación: 50 ns, programa: NAMD) Este virus es un virus de planta icosahedral pequeño que empeora los síntomas de infección por el virus del Mosaico del tabaco (TMV). Se utilizaron simulaciones de dinámica molecular para sondear los mecanismos de montaje viral. Toda la partícula STMV consiste en 60 copias idénticas de una proteína que componen el capside viral (coating), y un genoma RNA de 1063 nucleótido único. Un hallazgo clave es que el capsid es muy inestable cuando no hay ARN dentro. La simulación tomaría un ordenador de escritorio 2006 alrededor de 35 años para completar. Así se hizo en muchos procesadores en paralelo con la comunicación continua entre ellos.
• Simulaciones plegables de la pieza principal de Villin en todo el detalle del átomo (2006, Tamaño: 20.000 átomos; Tiempo de simulación: 500 μs= 500,000 ns, Programa: Folding@home) Esta simulación se ejecutó en 200.000 CPU de ordenadores personales participantes en todo el mundo. Estos ordenadores tenían instalado el programa Folding@home, un gran esfuerzo de computación distribuido coordinado por Vijay Pande en la Universidad de Stanford. Las propiedades cinéticas de la proteína Villin Headpiece fueron probadas utilizando muchas trayectorias independientes y cortas administradas por la CPU sin comunicación continua en tiempo real. Un método empleado fue el análisis de valor Pfold, que mide la probabilidad de plegar antes de desplegar una conformación inicial específica. Pfold da información sobre las estructuras estatales de transición y una orden de conformaciones a lo largo de la vía plegable. Cada trayectoria en un cálculo Pfold puede ser relativamente corta, pero se necesitan muchas trayectorias independientes.
• Se han realizado simulaciones de tráfico continuo largo en Anton, una supercomputadora masivamente paralela diseñada y construida alrededor de circuitos integrados específicos para aplicaciones personalizadas (ASIC) e interconexiones por D. E. Shaw Research. El resultado publicado más largo de una simulación realizada con Anton es una simulación de 1.112 milímetros de NTL9 a 355 K; también se realizó una segunda simulación independiente de 1.073 milímetros de esta configuración (y muchas otras simulaciones de más de 250 μs de tiempo químico continuo). In Cómo se mueven las proteínas, investigadores Kresten Lindorff-Larsen, Stefano Piana, Ron O. Dror y David E. Shaw discuten "los resultados de las simulaciones de dinámicas moleculares a nivel atómico, durante períodos que oscilan entre 100 μs y 1 ms, que revelan un conjunto de principios comunes subyacentes al plegado de 12 proteínas estructuralmente diversas". El examen de estas diversas trayectorias largas, habilitadas por hardware especializado y personalizado, les permite concluir que "en la mayoría de los casos, el plegamiento sigue una única ruta dominante en la que los elementos de la estructura nativa aparecen en un orden altamente correlativo con su propensión a formar en el estado desarrollado". En un estudio separado, Anton fue utilizado para realizar una simulación de 1.013 milisegundos de la dinámica nativa-estatal del inhibidor de tripasina pancreática bovina (BPTI) a 300 K.

Otra aplicación importante del método MD se beneficia de su capacidad de caracterización tridimensional y análisis de la evolución microestructural a escala atómica.

• Las simulaciones de MD se utilizan en la caracterización de la evolución del tamaño del grano, por ejemplo, al describir el desgaste y la fricción de los materiales de Al y Al (Zr). Dislocaciones La evolución y la evolución del tamaño del grano se analizan durante el proceso de fricción en esta simulación. Dado que el método MD proporcionó la información completa de la microestructura, la evolución del tamaño del grano se calculó en 3D utilizando los métodos de emparejamiento de la plantilla de Polyhedral, segmentación de granos y agrupación de Gráficos. En tal simulación, el método MD proporcionó una medición precisa del tamaño del grano. Utilizando esta información, se extrajeron, midieron y presentaron las estructuras de grano. Comparado con el método tradicional de usar SEM con una sola rebanada 2-dimensional del material, MD proporciona una manera 3-dimensional y precisa de caracterizar la evolución microestructural a escala atómica.

Algoritmos de dinámica molecular

• Potencias de Coulomb proyectadas modelo de solvente implícito

Integradores

• Integrador Symplectic
• Integración Verlet-Stoermer
• Integración Runge–Kutta
• Algoritmo de Beeman
• algoritmos constraint (para sistemas limitados)

Algoritmos de interacción de corto alcance

• Listas de células
• Lista de verificación
• Interacciones bonificadas

Algoritmos de interacción de largo alcance

• Summation Ewald
• Malla de partículas Summation (PME)
• Particle-particle-particle-mesh (P3M)
• Método de fuerza cambiada

Estrategias de paralelización

• Método de descomposición de dominios (Distribución de datos del sistema para computación paralela)

Dinámica molecular ab-initio

• Dinámica molecular del coche-Parrinello

Hardware especializado para simulaciones MD

• Anton – Un supercomputador especializado y masivo diseñado para ejecutar simulaciones MD
• MDGRAPE – Un sistema de propósito especial construido para simulaciones de dinámica molecular, especialmente la predicción de la estructura de proteínas

Tarjeta gráfica como hardware para simulaciones MD

simulación líquida iónica en GPU (Abalone)

El modelado molecular en GPU es la técnica de utilizar una unidad de procesamiento gráfico (GPU) para simulaciones moleculares.

En 2007, NVIDIA introdujo tarjetas de vídeo que podrían utilizarse no sólo para mostrar gráficos sino también para cálculos científicos. Estas tarjetas incluyen muchas unidades aritméticas (en 2016, hasta 3,584 en Tesla P100) trabajando en paralelo. Mucho antes de este evento, el poder computacional de las tarjetas de vídeo se utilizó exclusivamente para acelerar cálculos gráficos. Lo nuevo es que NVIDIA hizo posible desarrollar programas paralelos en una interfaz de programación de aplicaciones de alto nivel (API) llamada CUDA. Esta tecnología simplifica sustancialmente la programación permitiendo que los programas estén escritos en C/C++. Más recientemente, OpenCL permite acelerar la GPU multiplataforma.