Dinámica de cuerpos rígidos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En la ciencia física de la dinámica, la dinámica de cuerpos rígidos estudia el movimiento de sistemas de cuerpos interconectados bajo la acción de fuerzas externas. La suposición de que los cuerpos son rígidos (es decir, no se deforman bajo la acción de las fuerzas aplicadas) simplifica el análisis, al reducir los parámetros que describen la configuración del sistema a la traslación y rotación de marcos de referencia unidos a cada cuerpo. Esto excluye los cuerpos que muestran un comportamiento fluido, altamente elástico y plástico.

La dinámica de un sistema de cuerpo rígido se describe mediante las leyes de la cinemática y mediante la aplicación de la segunda ley de Newton (cinética) o su forma derivada, la mecánica de Lagrange. La solución de estas ecuaciones de movimiento proporciona una descripción de la posición, el movimiento y la aceleración de los componentes individuales del sistema y, en general, del sistema mismo, en función del tiempo. La formulación y solución de la dinámica de cuerpos rígidos es una herramienta importante en la simulación por computadora de sistemas mecánicos.

Dinámica plana de cuerpo rígido

Si un sistema de partículas se mueve paralelamente a un plano fijo, se dice que el sistema está restringido al movimiento plano. En este caso, las leyes de Newton (cinética) para un sistema rígido de N partículas, P _i, i =1,..., N, se simplifican porque no hay movimiento en la dirección k. Determine la fuerza y el par resultantes en un punto de referencia R, para obtener

{displaystyle mathbf {F} =sum_{i=1}^{N}m_{i}mathbf {A}_{i},quad mathbf {T} =sum_{i=1 }^{N}(mathbf {r} _{i}-mathbf {R})times m_{i}mathbf {A} _{i},}

donde r _i denota la trayectoria plana de cada partícula.

La cinemática de un cuerpo rígido produce la fórmula para la aceleración de la partícula Pi _en términos de la posición R y la aceleración A de la partícula de referencia, así como el vector de velocidad angular ω y el vector de aceleración angular α del sistema rígido de partículas como,

{displaystyle mathbf {A} _{i}={boldsymbol {alpha }}times (mathbf {r} _{i}-mathbf {R})+{boldsymbol {omega }} veces ({boldsymbol {omega }}times (mathbf {r} _{i}-mathbf {R}))+mathbf {A}.}

Para los sistemas que están restringidos al movimiento plano, los vectores de velocidad angular y aceleración angular se dirigen a lo largo de k perpendicular al plano de movimiento, lo que simplifica esta ecuación de aceleración. En este caso, los vectores de aceleración se pueden simplificar introduciendo los vectores unitarios e _i desde el punto de referencia R hasta un punto r _i y los vectores unitarios ${estilo de texto mathbf {t} _{i}=mathbf {k} times mathbf {e} _{i}}$ , por lo que

{displaystylemathbf{A}_{i}=alpha(Delta r_{i}mathbf{t}_{i})-omega^{2}(Delta r_{i}mathbf{e } _{i})+mathbf{A}.}

Esto produce la fuerza resultante sobre el sistema como

{displaystyle mathbf {F} =alpha sum _{i=1}^{N}m_{i}left(Delta r_{i}mathbf {t}_{i}right)- omega ^{2}sum_{i=1}^{N}m_{i}left(Delta r_{i}mathbf {e}_{i}right)+left(sum_{ i=1}^{N}m_{i}right)mathbf {A},}

y par como

{displaystyle {begin{alineado}mathbf {T} ={}&sum_{i=1}^{N}(m_{i}Delta r_{i}mathbf {e}_{i})times left(alpha (Delta r_{i}mathbf {t} _{i})-omega ^{2}(Delta r_{i}mathbf {e} _{i})+ mathbf {A} right)\{}={}&left(sum _{i=1}^{N}m_{i}Delta r_{i}^{2}right)alpha mathbf {k} +left(sum _{i=1}^{N}m_{i}Delta r_{i}mathbf {e} _{i}right)times mathbf {A},end{alineado}}}

donde ${estilo de texto mathbf {e} _{i}times mathbf {e} _{i}=0}$ y ${textstyle mathbf {e} _{i}times mathbf {t} _{i}=mathbf {k} }$ es el vector unitario perpendicular al plano para todas las partículas P _i.

Utilice el centro de masa C como punto de referencia, por lo que estas ecuaciones para las leyes de Newton se simplifican para convertirse en

{displaystylemathbf{F}=Mmathbf{A},quadmathbf{T}=I_{textbf{C}}alphamathbf{k},}

donde M es la masa total e I _C es el momento de inercia alrededor de un eje perpendicular al movimiento del sistema rígido y que pasa por el centro de masa.

Cuerpo rígido en tres dimensiones

Descripciones de orientación o actitud

Se han desarrollado varios métodos para describir las orientaciones de un cuerpo rígido en tres dimensiones. Se resumen en las siguientes secciones.

ángulos de Euler

El primer intento de representar una orientación se atribuye a Leonhard Euler. Imaginó tres marcos de referencia que podían rotar uno alrededor del otro y se dio cuenta de que comenzando con un marco de referencia fijo y realizando tres rotaciones, podía obtener cualquier otro marco de referencia en el espacio (usando dos rotaciones para fijar el eje vertical y otra para fijar los otros dos ejes). Los valores de estas tres rotaciones se denominan ángulos de Euler. Comúnmente, $psi$ se usa para denotar precesión, $theta$ nutación y $fi$ rotación intrínseca.

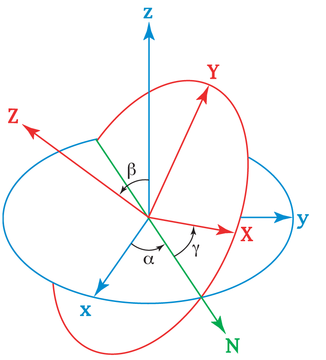Diagrama de los ángulos de Euler
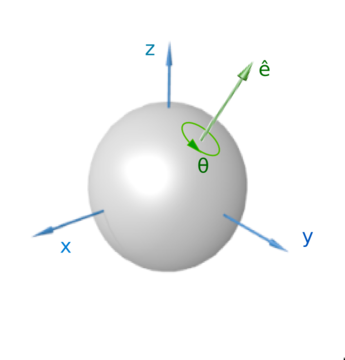Rotación intrínseca de una pelota alrededor de un eje fijo.
Movimiento de un trompo en los ángulos de Euler.

Ángulos de Tait-Bryan

Estos son tres ángulos, también conocidos como guiñada, cabeceo y balanceo, ángulos de navegación y ángulos cardánicos. Matemáticamente constituyen un conjunto de seis posibilidades dentro de los doce conjuntos posibles de ángulos de Euler, siendo la ordenación la que mejor se utiliza para describir la orientación de un vehículo como un avión. En ingeniería aeroespacial se les suele denominar ángulos de Euler.

Vector de orientación

Euler también se dio cuenta de que la composición de dos rotaciones es equivalente a una sola rotación sobre un eje fijo diferente (teorema de rotación de Euler). Por lo tanto, la composición de los primeros tres ángulos tiene que ser igual a una sola rotación, cuyo eje fue complicado de calcular hasta que se desarrollaron las matrices.

Basado en este hecho, introdujo una forma vectorial de describir cualquier rotación, con un vector en el eje de rotación y un módulo igual al valor del ángulo. Por lo tanto, cualquier orientación se puede representar mediante un vector de rotación (también llamado vector de Euler) que conduce a ella desde el marco de referencia. Cuando se utiliza para representar una orientación, el vector de rotación se denomina comúnmente vector de orientación o vector de actitud.

Un método similar, llamado representación de eje-ángulo, describe una rotación u orientación usando un vector unitario alineado con el eje de rotación y un valor separado para indicar el ángulo (ver figura).

Matriz de orientación

Con la introducción de las matrices se reescribieron los teoremas de Euler. Las rotaciones se describieron mediante matrices ortogonales denominadas matrices de rotación o matrices de coseno director. Cuando se utiliza para representar una orientación, una matriz de rotación se denomina comúnmente matriz de orientación o matriz de actitud.

El vector de Euler mencionado anteriormente es el vector propio de una matriz de rotación (una matriz de rotación tiene un valor propio real único). El producto de dos matrices de rotación es la composición de rotaciones. Por lo tanto, como antes, la orientación se puede dar como la rotación desde el marco inicial para lograr el marco que queremos describir.

El espacio de configuración de un objeto no simétrico en un espacio n -dimensional es SO(n) × R. La orientación se puede visualizar adjuntando una base de vectores tangentes a un objeto. La dirección en la que apunta cada vector determina su orientación.

Cuaternión de orientación

Otra forma de describir las rotaciones es usando cuaterniones de rotación, también llamados versores. Son equivalentes a matrices de rotación y vectores de rotación. Con respecto a los vectores de rotación, se pueden convertir más fácilmente ay desde matrices. Cuando se utilizan para representar orientaciones, los cuaterniones de rotación suelen denominarse cuaterniones de orientación o cuaterniones de actitud.

La segunda ley de Newton en tres dimensiones.

Para considerar la dinámica de un cuerpo rígido en el espacio tridimensional, la segunda ley de Newton debe extenderse para definir la relación entre el movimiento de un cuerpo rígido y el sistema de fuerzas y pares que actúan sobre él.

Newton formuló su segunda ley para una partícula como: "El cambio de movimiento de un objeto es proporcional a la fuerza aplicada y se realiza en la dirección de la línea recta en la que se aplica la fuerza". Debido a que Newton generalmente se refirió a la masa por la velocidad como el "movimiento" de una partícula, la frase "cambio de movimiento" se refiere a la masa por la aceleración de la partícula, por lo que esta ley generalmente se escribe como

donde se entiende que F es la única fuerza externa que actúa sobre la partícula, m es la masa de la partícula y a es su vector aceleración. La extensión de la segunda ley de Newton a cuerpos rígidos se logra considerando un sistema rígido de partículas.

Sistema rígido de partículas

Si un sistema de N partículas, P _i, i=1,..., N, se ensamblan en un cuerpo rígido, entonces la segunda ley de Newton se puede aplicar a cada una de las partículas del cuerpo. Si F _i es la fuerza externa aplicada a la partícula P _i con masa m _i, entonces

{displaystyle mathbf {F}_{i}+sum_{j=1}^{N}mathbf {F}_{ij}=m_{i}mathbf {a}_{i}, cuádruple i=1,ldots,N,}

donde F _ij es la fuerza interna de la partícula P _j que actúa sobre la partícula P _i que mantiene la distancia constante entre estas partículas.

Se obtiene una simplificación importante de estas ecuaciones de fuerza introduciendo la fuerza y el par resultantes que actúan sobre el sistema rígido. Esta fuerza y torque resultantes se obtienen eligiendo una de las partículas en el sistema como punto de referencia, R, donde cada una de las fuerzas externas se aplica con la adición de un torque asociado. La fuerza resultante F y el par T están dados por las fórmulas,

{displaystyle mathbf {F} =sum_{i=1}^{N}mathbf {F}_{i},quad mathbf {T} =sum_{i=1}^{N }(mathbf {R} _{i}}mathbf {R})times mathbf {F} _{i},}

donde R _i es el vector que define la posición de la partícula P _i.

La segunda ley de Newton para una partícula se combina con estas fórmulas para que la fuerza y el par resultantes produzcan,

donde las fuerzas internas F _ij se cancelan por pares. La cinemática de un cuerpo rígido produce la fórmula para la aceleración de la partícula Pi _en términos de la posición R y la aceleración a de la partícula de referencia, así como el vector de velocidad angular ω y el vector de aceleración angular α del sistema rígido de partículas como,

{displaystylemathbf{a}_{i}=alphatimes(mathbf{R}_{i}-mathbf{R})+omegatimes(omegatimes(mathbf{R}) _{i}-mathbf{R}))+mathbf{a}.}

Propiedades de masa

Las propiedades de masa del cuerpo rígido están representadas por su centro de masa y matriz de inercia. Elija el punto de referencia R para que satisfaga la condición

{displaystyle sum_{i=1}^{N}m_{i}(mathbf {R}_{i}-mathbf {R})=0,}

entonces se le conoce como el centro de masa del sistema.

La matriz de inercia [I _R ] del sistema relativa al punto de referencia R está definida por

{displaystyle [I_{R}]=sum_{i=1}^{N}m_{i}left(mathbf {I} left(mathbf {S}_{i}^{textsf {T}}mathbf {S}_{i}right)-mathbf {S}_{i}mathbf {S}_{i}^{textsf {T}}right),}

donde ${mathbf{S}}_{i}$ está el vector columna R _i − R; ${displaystyle mathbf {S} _{i}^{textsf {T}}}$ es su traspuesta, y $mathbf{yo}$ es la matriz identidad de 3 por 3.

${displaystyle mathbf {S}_{i}^{textsf {T}}mathbf {S}_{i}}$ es el producto escalar de ${mathbf{S}}_{i}$ consigo mismo, mientras que ${displaystyle mathbf {S} _{i}mathbf {S} _{i}^{textsf {T}}}$ es el producto tensorial de ${mathbf{S}}_{i}$ consigo mismo.

Ecuaciones fuerza-torque

Usando el centro de masa y la matriz de inercia, las ecuaciones de fuerza y torque para un solo cuerpo rígido toman la forma

{displaystylemathbf{F}=mmathbf{a},quadmathbf{T}=[I_{R}]alpha+omegatimes[I_{R}]omega,}

y se conocen como la segunda ley de movimiento de Newton para un cuerpo rígido.

La dinámica de un sistema interconectado de cuerpos rígidos, B _i, j = 1,..., M, se formula aislando cada cuerpo rígido e introduciendo las fuerzas de interacción. La resultante de las fuerzas externas y de interacción en cada cuerpo da las ecuaciones fuerza-torque

{displaystyle mathbf {F}_{j}=m_{j}mathbf {a}_{j},quad mathbf {T}_{j}=[I_{R}]_{j} alfa _ {j}+omega _ {j}times [I_{R}]_{j}omega_{j},quad j=1,ldots,M.}

La formulación de Newton produce 6 M ecuaciones que definen la dinámica de un sistema de M cuerpos rígidos.

Rotación en tres dimensiones

Un objeto giratorio, ya sea bajo la influencia de pares o no, puede exhibir los comportamientos de precesión y nutación. La ecuación fundamental que describe el comportamiento de un cuerpo sólido en rotación es la ecuación de movimiento de Euler:

{displaystyle {boldsymbol {tau }}={frac {Dmathbf {L} }{Dt}}={frac {dmathbf {L} }{dt}}+{boldsymbol {omega }}times mathbf {L} ={frac {d(I{boldsymbol {omega }})}{dt}}+{boldsymbol {omega }}times {I{boldsymbol {omega }}}=I{boldsymbol {alpha }}+{boldsymbol {omega }}times {I{boldsymbol {omega }}}}

donde los pseudovectores τ y L son, respectivamente, los pares sobre el cuerpo y su momento angular, el escalar I es su momento de inercia, el vector ω es su velocidad angular, el vector α es su aceleración angular, D es el diferencial en un marco de referencia inercial y d es el diferencial en un marco de referencia relativo fijo con el cuerpo.

La solución a esta ecuación cuando no hay torque aplicado se discute en los artículos Ecuación de movimiento de Euler y Elipsoide de Poinsot.

De la ecuación de Euler se deduce que un par τ aplicado perpendicularmente al eje de rotación y, por lo tanto, perpendicular a L, da como resultado una rotación alrededor de un eje perpendicular tanto a τ como a L. Este movimiento se llama precesión. La velocidad angular de precesión Ω _P viene dada por el producto vectorial:

{displaystyle {boldsymbol {tau }}={boldsymbol {Omega }}_{mathrm {P} }times mathbf {L}.}

La precesión se puede demostrar colocando un trompo con su eje horizontal y apoyado sin apretar (sin fricción hacia la precesión) en un extremo. En lugar de caer, como cabría esperar, la peonza parece desafiar la gravedad al permanecer con su eje horizontal, cuando el otro extremo del eje se deja sin apoyo y el extremo libre del eje describe lentamente un círculo en un plano horizontal, el resultado giro de precesión. Este efecto se explica por las ecuaciones anteriores. El par en la parte superior es proporcionado por un par de fuerzas: la gravedad que actúa hacia abajo sobre el centro de masa del dispositivo y una fuerza igual que actúa hacia arriba para sostener un extremo del dispositivo. La rotación resultante de este torque no es hacia abajo, como podría esperarse intuitivamente, lo que hace que el dispositivo se caiga,

Bajo un par constante de magnitud τ, la velocidad de precesión Ω _P es inversamente proporcional a L, la magnitud de su momento angular:

{displaystyle tau ={mathit {Omega }}_{mathrm {P} }Lsin theta,}

donde θ es el ángulo entre los vectores Ω _P y L. Por lo tanto, si el giro de la peonza disminuye (por ejemplo, debido a la fricción), su momento angular disminuye y, por lo tanto, aumenta la velocidad de precesión. Esto continúa hasta que el dispositivo no puede girar lo suficientemente rápido para soportar su propio peso, cuando deja de preceder y se cae de su soporte, principalmente porque la fricción contra la precesión provoca otra precesión que provoca la caída.

Por convención, estos tres vectores (torque, espín y precesión) están orientados entre sí de acuerdo con la regla de la mano derecha.

Trabajo virtual de las fuerzas que actúan sobre un cuerpo rígido

Una formulación alternativa de la dinámica del cuerpo rígido que tiene varias características convenientes se obtiene al considerar el trabajo virtual de las fuerzas que actúan sobre un cuerpo rígido.

El trabajo virtual de las fuerzas que actúan en varios puntos sobre un solo cuerpo rígido se puede calcular utilizando las velocidades de su punto de aplicación y la fuerza y el par resultantes. Para ver esto, dejemos que las fuerzas F ₁, F ₂... F _n actúen sobre los puntos R ₁, R ₂... R _n en un cuerpo rígido.

Las trayectorias de R _i, i = 1,..., n están definidas por el movimiento del cuerpo rígido. Las velocidades de los puntos R _i a lo largo de sus trayectorias son

{displaystyle mathbf {V} _{i}={boldsymbol {omega }}times (mathbf {R} _{i}-mathbf {R})+mathbf {V},}

donde ω es el vector de velocidad angular del cuerpo.

Trabajo virtual

El trabajo se calcula a partir del producto punto de cada fuerza con el desplazamiento de su punto de contacto

{displaystyle delta W=sum _{i=1}^{n}mathbf {F} _{i}cdot delta mathbf {r} _{i}.}

Si la trayectoria de un cuerpo rígido está definida por un conjunto de coordenadas generalizadas q _j, j = 1,..., m, entonces los desplazamientos virtuales δ r _i están dados por

{displaystyle delta mathbf {r} _{i}=sum _{j=1}^{m}{frac {parcial mathbf {r} _{i}}{parcial q_{j} }}delta q_{j}=sum _{j=1}^{m}{frac {parcial mathbf {V} _{i}}{parcial {dot {q}}_{j }}}deltaq_{j}.}

El trabajo virtual de este sistema de fuerzas que actúan sobre el cuerpo en términos de las coordenadas generalizadas se convierte en

{displaystyle delta W=mathbf {F} _{1}cdot left(sum _{j=1}^{m}{frac {parcial mathbf {V} _{1}}{ parcial {dot {q}}_{j}}}delta q_{j}right)+dots +mathbf {F} _{n}cdot left(sum _{j=1} ^{m}{frac {parcial mathbf {V} _{n}}{parcial {dot {q}}_{j}}}delta q_{j}right)}

o recogiendo los coeficientes de δq _j

{displaystyle delta W=left(sum _{i=1}^{n}mathbf {F} _{i}cdot {frac {parcial mathbf {V} _{i}}{ parcial {dot {q}}_{1}}}right)delta q_{1}+dots +left(sum_{1=1}^{n}mathbf {F}_{ i}cdot {frac {parcial mathbf {V} _{i}}{parcial {dot {q}}_{m}}}right)delta q_{m}.}

Fuerzas generalizadas

Para simplificar, considere una trayectoria de un cuerpo rígido que se especifica mediante una sola coordenada generalizada q, como un ángulo de rotación, luego la fórmula se convierte en

{displaystyle delta W=left(sum _{i=1}^{n}mathbf {F} _{i}cdot {frac {parcial mathbf {V} _{i}}{ parcial {dot {q}}}}right)delta q=left(sum _{i=1}^{n}mathbf {F} _{i}cdot {frac {parcial ({boldsymbol {omega }}times (mathbf {R} _{i}-mathbf {R})+mathbf {V})}{parcial {dot {q}}}}right)delta q.}

Introduzca la fuerza resultante F y el par T para que esta ecuación tome la forma

{displaystyle delta W=left(mathbf {F} cdot {frac {parcial mathbf {V} }{parcial {dot {q}}}}+mathbf {T} cdot { frac {parcial {boldsymbol {omega }}}{parcial {dot {q}}}}right)delta q.}

La cantidad Q definida por

{displaystyle Q=mathbf {F} cdot {frac {parcial mathbf {V} }{parcial {dot {q}}}}+mathbf {T} cdot {frac {parcial {boldsymbol {omega }}}{parcial {dot {q}}}},}

se conoce como la fuerza generalizada asociada con el desplazamiento virtual δq. Esta fórmula se generaliza al movimiento de un cuerpo rígido definido por más de una coordenada generalizada, es decir

{displaystyle delta W=sum _{j=1}^{m}Q_{j}delta q_{j},}

dónde

{displaystyle Q_{j}=mathbf {F} cdot {frac {parcial mathbf {V} }{parcial {dot {q}}_{j}}}+mathbf {T} cdot {frac {parcial {boldsymbol {omega }}}{parcial {dot {q}}_{j}}},quad j=1,ldots,m.}

Es útil señalar que las fuerzas conservativas, como la gravedad y las fuerzas de resorte, se derivan de una función potencial V (q ₁,..., q _n), conocida como energía potencial. En este caso las fuerzas generalizadas vienen dadas por

{displaystyle Q_{j}=-{frac {parcial V}{parcial q_{j}}},quad j=1,ldots,m.}

Forma de D'Alembert del principio del trabajo virtual

Las ecuaciones de movimiento para un sistema mecánico de cuerpos rígidos se pueden determinar usando la forma de D'Alembert del principio del trabajo virtual. El principio del trabajo virtual se usa para estudiar el equilibrio estático de un sistema de cuerpos rígidos, sin embargo, al introducir términos de aceleración en las leyes de Newton, este enfoque se generaliza para definir el equilibrio dinámico.

Equilibrio estático

El equilibrio estático de un sistema mecánico de cuerpos rígidos se define por la condición de que el trabajo virtual de las fuerzas aplicadas sea cero para cualquier desplazamiento virtual del sistema. Esto se conoce como el principio del trabajo virtual. Esto es equivalente al requisito de que las fuerzas generalizadas para cualquier desplazamiento virtual sean cero, es decir Q _i =0.

Sea un sistema mecánico construido a partir de n cuerpos rígidos, B _i, i = 1,..., n, y sea la resultante de las fuerzas aplicadas sobre cada cuerpo los pares fuerza-par, F _i y T _i, i = 1,..., norte. Note que estas fuerzas aplicadas no incluyen las fuerzas de reacción donde los cuerpos están conectados. Finalmente, suponga que la velocidad V _i y las velocidades angulares ω _i, i = 1,..., n, para cada cuerpo rígido, están definidos por una sola coordenada generalizada q. Se dice que tal sistema de cuerpos rígidos tiene un grado de libertad.

El trabajo virtual de las fuerzas y pares, F _i y T _i, aplicado a este sistema de un grado de libertad está dado por

{displaystyle delta W=sum _{i=1}^{n}left(mathbf {F} _{i}cdot {frac {parcial mathbf {V} _{i}}{ parcial {dot {q}}}}+mathbf {T} _{i}cdot {frac {parcial {boldsymbol {omega }}_{i}}{parcial {dot {q }}}}derecha)delta q=Qdelta q,}

dónde

{displaystyle Q=sum_{i=1}^{n}left(mathbf {F}_{i}cdot {frac {parcial mathbf {V}_{i}}{parcial {dot {q}}}}+mathbf {T} _{i}cdot {frac {parcial {boldsymbol {omega }}_{i}}{parcial {dot {q}} }}Correcto),}

es la fuerza generalizada que actúa sobre este sistema de un grado de libertad.

Si el sistema mecánico está definido por m coordenadas generalizadas, q _j, j = 1,..., m, entonces el sistema tiene m grados de libertad y el trabajo virtual viene dado por,

dónde

{displaystyle Q_{j}=sum_{i=1}^{n}left(mathbf {F}_{i}cdot {frac {parcial mathbf {V}_{i}} {parcial {dot {q}}_{j}}}+mathbf {T}_{i}cdot {frac {parcial {boldsymbol {omega }}_{i}}{parcial {dot {q}}_{j}}}right),quad j=1,ldots,m.}

es la fuerza generalizada asociada con la coordenada generalizada q _j. El principio del trabajo virtual establece que el equilibrio estático ocurre cuando estas fuerzas generalizadas que actúan sobre el sistema son cero, es decir

{displaystyle Q_{j}=0,quad j=1,ldots,m.}

Estas m ecuaciones definen el equilibrio estático del sistema de cuerpos rígidos.

Fuerzas de inercia generalizadas

Considere un solo cuerpo rígido que se mueve bajo la acción de una fuerza resultante F y un momento de torsión T, con un grado de libertad definido por la coordenada generalizada q. Suponga que el punto de referencia para la fuerza y el par resultantes es el centro de masa del cuerpo, entonces la fuerza de inercia generalizada Q* asociada con la coordenada generalizada q viene dada por

{displaystyle Q^{*}=-(Mmathbf {A})cdot {frac {parcial mathbf {V} }{parcial {dot {q}}}}-left([I_ {R}]{boldsymbol {alpha }}+{boldsymbol {omega }}times [I_{R}]{boldsymbol {omega }}right)cdot {frac {parcial { boldsymbol {omega }}}{parcial {dot {q}}}}.}

Esta fuerza de inercia se puede calcular a partir de la energía cinética del cuerpo rígido,

{displaystyle T={tfrac {1}{2}}Mmathbf {V} cdot mathbf {V} +{tfrac {1}{2}}{boldsymbol {omega }}cdot [ I_{R}]{boldsymbol {omega}},}

mediante el uso de la fórmula

{displaystyle Q^{*}=-left({frac {d}{dt}}{frac {parcial T}{parcial {dot {q}}}}-{frac {parcial T}{q parcial}}right).}

Un sistema de n cuerpos rígidos con m coordenadas generalizadas tiene la energía cinética

{displaystyle T=sum_{i=1}^{n}left({tfrac {1}{2}}Mmathbf {V}_{i}cdot mathbf {V}_{i }+{tfrac {1}{2}}{boldsymbol {omega }}_{i}cdot [I_{R}]{boldsymbol {omega }}_{i}right),}

que se puede utilizar para calcular las m fuerzas de inercia generalizadas

{displaystyle Q_{j}^{*}=-left({frac {d}{dt}}{frac {parcial T}{parcial {dot {q}}_{j}}} -{frac {T parcial}{q_{j}}}parcialright),quad j=1,ldots,m.}

Equilibrio dinámico

La forma de D'Alembert del principio del trabajo virtual establece que un sistema de cuerpos rígidos está en equilibrio dinámico cuando el trabajo virtual de la suma de las fuerzas aplicadas y las fuerzas de inercia es cero para cualquier desplazamiento virtual del sistema. Así, el equilibrio dinámico de un sistema de n cuerpos rígidos con m coordenadas generalizadas requiere que

{displaystyle delta W=left(Q_{1}+Q_{1}^{*}right)delta q_{1}+dots +left(Q_{m}+Q_{m}^{ *}derecha)delta q_{m}=0,}

para cualquier conjunto de desplazamientos virtuales δq _j. Esta condición produce m ecuaciones,

{displaystyle Q_{j}+Q_{j}^{*}=0,quad j=1,ldots,m,}

que también se puede escribir como

{displaystyle {frac {d}{dt}}{frac {parcial T}{parcial {dot {q}}_{j}}}-{frac {parcial T}{parcial q_ {j}}}=Q_{j},quad j=1,ldots,m.}

El resultado es un conjunto de m ecuaciones de movimiento que definen la dinámica del sistema de cuerpo rígido.

Las ecuaciones de Lagrange

Si las fuerzas generalizadas Q _j son derivables de una energía potencial V (q ₁,..., q _m), entonces estas ecuaciones de movimiento toman la forma

{displaystyle {frac {d}{dt}}{frac {parcial T}{parcial {dot {q}}_{j}}}-{frac {parcial T}{parcial q_ {j}}}=-{frac {V parcial}{q_ parcial{j}}},quad j=1,ldots,m.}

En este caso, introduzca el Lagrangiano, L = T − V, para que estas ecuaciones de movimiento se conviertan en

{displaystyle {frac {d}{dt}}{frac {parcial L}{parcial {dot {q}}_{j}}}-{frac {parcial L}{parcial q_ {j}}}=0quad j=1,ldots,m.}

Éstas se conocen como ecuaciones de movimiento de Lagrange.

Momento lineal y angular

Sistema de partículas

El momento lineal y angular de un sistema rígido de partículas se formula midiendo la posición y la velocidad de las partículas en relación con el centro de masa. Sea el sistema de partículas P _i, i = 1,..., n ubicado en las coordenadas r _i y velocidades v _i. Seleccione un punto de referencia R y calcule la posición relativa y los vectores de velocidad,

{displaystyle mathbf {r} _{i}=left(mathbf {r} _{i}-mathbf {R} right)+mathbf {R},quad mathbf {v}_{ i}={frac {d}{dt}}(mathbf {r} _{i}-mathbf {R})+mathbf {V}.}

Los vectores de momento lineal y angular totales en relación con el punto de referencia R son

{displaystyle mathbf {p} ={frac {d}{dt}}left(sum_{i=1}^{n}m_{i}left(mathbf {r}_{i} -mathbf {R} right)right)+left(sum _{i=1}^{n}m_{i}right)mathbf {V},}

{displaystyle mathbf {L} =sum_{i=1}^{n}m_{i}left(mathbf {r}_{i}-mathbf {R} right)times { fracción {d}{dt}}left(mathbf {r} _{i}-mathbf {R} right)+left(sum _{i=1}^{n}m_{i} izquierda(mathbf {r} _{i}-mathbf {R} derecha)derecha)veces mathbf {V}.}

Si se elige R como el centro de masa, estas ecuaciones se simplifican a

{displaystyle mathbf {p} =Mmathbf {V},quad mathbf {L} =sum_{i=1}^{n}m_{i}left(mathbf {r}_{ i}-mathbf {R} right)times {frac {d}{dt}}left(mathbf {r} _{i}-mathbf {R} right).}

Sistema rígido de partículas

Para especializar estas fórmulas en un cuerpo rígido, suponga que las partículas están rígidamente conectadas entre sí, de modo que P _i, i=1,...,n están ubicadas por las coordenadas r _i y las velocidades v _i. Seleccione un punto de referencia R y calcule la posición relativa y los vectores de velocidad,

{displaystylemathbf{r}_{i}=(mathbf{r}_{i}-mathbf{R})+mathbf{R},quadmathbf{v}_{i}= omegatimes(mathbf{r}_{i}-mathbf{R})+mathbf{V},}

donde ω es la velocidad angular del sistema.

El momento lineal y el momento angular de este sistema rígido medidos en relación con el centro de masa R es

{displaystyle mathbf {p} =left(sum _{i=1}^{n}m_{i}right)mathbf {V},quad mathbf {L} =sum_{i =1}^{n}m_{i}(mathbf {r} _{i}}mathbf {R})times mathbf {v} _{i}=sum _{i=1}^{ n}m_{i}(mathbf {r} _{i}-mathbf {R})times (omega times (mathbf {r} _{i}}mathbf {R})).}

Estas ecuaciones se simplifican para convertirse en,

{displaystylemathbf{p}=Mmathbf{V},quadmathbf{L}=[I_{R}]omega,}

donde M es la masa total del sistema y [I _R ] es la matriz de momento de inercia definida por

{displaystyle [I_{R}]=-sum_{i=1}^{n}m_{i}[r_{i}-R][r_{i}-R],}

donde [r _i − R] es la matriz simétrica oblicua construida a partir del vector r _i − R.

Aplicaciones

Para el análisis de sistemas robóticos
Para el análisis biomecánico de animales, humanos o sistemas humanoides
Para el análisis de objetos espaciales
Para la comprensión de movimientos extraños de cuerpos rígidos.
Para el diseño y desarrollo de sensores basados en la dinámica, como los sensores giroscópicos.
Para el diseño y desarrollo de diversas aplicaciones de mejora de la estabilidad en automóviles.
Para mejorar los gráficos de videojuegos que involucran cuerpos rígidos

Contenido relacionado

Más resultados...