Dimensión fractal

11.5 x 200 = 2300 km

28 x 100 = 2800 km

70 x 50 = 3500 km

Gráfico 1 A medida que la longitud del bastón de medición se escala más pequeña y menor, la longitud total de la costa mide aumentos (ver paradoja costera).

En matemáticas, una dimensión fractal es un término invocado en la ciencia de la geometría para proporcionar un índice estadístico racional de los detalles de complejidad en un patrón. Un patrón fractal cambia con la escala en la que se mide. También es una medida de la capacidad de llenado de espacio de un patrón, e indica cómo un fractal se escala de manera diferente, en una dimensión fractal (no entera).

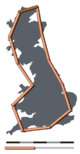
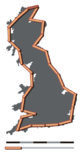
La idea principal de "fracturado" dimensiones tiene una larga historia en las matemáticas, pero el término mismo fue puesto en primer plano por Benoit Mandelbrot basado en su artículo de 1967 sobre la autosimilitud en el que discutió las dimensiones fraccionarias. En ese artículo, Mandelbrot citó un trabajo anterior de Lewis Fry Richardson que describe la noción contraria a la intuición de que la longitud medida de una costa cambia con la longitud de la vara de medir utilizada (ver Fig. 1). En términos de esa noción, la dimensión fractal de una línea de costa cuantifica cómo cambia el número de varas de medir a escala requeridas para medir la línea de costa con la escala aplicada a la vara. Hay varias definiciones matemáticas formales de dimensión fractal que se basan en este concepto básico de cambio en detalle con cambio de escala: consulte la sección Ejemplos.

Finalmente, el término dimensión fractal se convirtió en la frase con la que el propio Mandelbrot se sintió más cómodo con respecto a encapsular el significado de la palabra fractal, un término que él mismo creó. Después de varias iteraciones a lo largo de los años, Mandelbrot se decidió por este uso del lenguaje: "... usar fractal sin una definición pedante, usar dimensión fractal como término genérico aplicable a todas las variantes."

Un ejemplo no trivial es la dimensión fractal de un copo de nieve de Koch. Tiene una dimensión topológica de 1, pero de ninguna manera es rectificable: la longitud de la curva entre dos puntos cualesquiera del copo de nieve de Koch es infinita. Ninguna pequeña parte de él es como una línea, sino que está compuesto por un número infinito de segmentos unidos en diferentes ángulos. La dimensión fractal de una curva se puede explicar intuitivamente pensando en una línea fractal como un objeto demasiado detallado para ser unidimensional, pero demasiado simple para ser bidimensional. Por lo tanto, su dimensión podría describirse mejor no por su dimensión topológica habitual de 1, sino por su dimensión fractal, que a menudo es un número entre uno y dos; en el caso del copo de nieve de Koch, es aproximadamente 1,2619.

Introducción

Gráfico 2 A 32-segment quadric fractal escalado y visto a través de cajas de diferentes tamaños. El patrón ilustra la similitud de uno mismo. La dimensión fractal teórica para este fractal es 5/3 Ω 1.67; su dimensión fractal empírica del análisis de recuento de caja es ±1% utilizando software de análisis fractal.

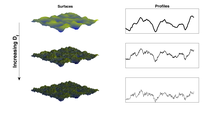
Una dimensión fractal es un índice para caracterizar patrones o conjuntos fractales al cuantificar su complejidad como una relación entre el cambio en detalle y el cambio en escala. Varios tipos de dimensión fractal se pueden medir teórica y empíricamente (ver Fig. 2). Las dimensiones fractales se utilizan para caracterizar un amplio espectro de objetos que van desde lo abstracto hasta los fenómenos prácticos, incluidas las turbulencias, las redes fluviales, el crecimiento urbano, la fisiología humana, la medicina y las tendencias del mercado. La idea esencial de las dimensiones fraccionales o fractales tiene una larga historia en las matemáticas que se remonta al siglo XVII, pero los términos fractal y dimensiones fractales fueron acuñadas por el matemático Benoit Mandelbrot en 1975.

dimensiones fractales se aplicaron por primera vez como un índice que caracterizaba formas geométricas complicadas para las que los detalles parecían más importantes que la imagen general. Para conjuntos que describen formas geométricas ordinarias, la dimensión fractal teórica es igual a la familiar dimensión euclidiana o topológica del conjunto. Por lo tanto, es 0 para conjuntos que describen puntos (conjuntos de dimensión 0); 1 para conjuntos que describen líneas (conjuntos unidimensionales que solo tienen longitud); 2 para conjuntos que describen superficies (conjuntos bidimensionales que tienen largo y ancho); y 3 para conjuntos que describen volúmenes (conjuntos tridimensionales que tienen largo, ancho y alto). Pero esto cambia para los conjuntos fractales. Si la dimensión fractal teórica de un conjunto excede su dimensión topológica, se considera que el conjunto tiene geometría fractal.

A diferencia de las dimensiones topológicas, el índice fractal puede tomar valores no enteros, lo que indica que un conjunto llena su espacio cualitativa y cuantitativamente de forma diferente a como lo hace un conjunto geométrico ordinario. Por ejemplo, una curva con una dimensión fractal muy cercana a 1, digamos 1,10, se comporta como una línea ordinaria, pero una curva con una dimensión fractal de 1,9 serpentea a través del espacio casi como una superficie. De manera similar, una superficie con una dimensión fractal de 2,1 llena el espacio de manera muy similar a una superficie ordinaria, pero una con una dimensión fractal de 2,9 se pliega y fluye para llenar el espacio casi como un volumen. Esta relación general se puede ver en las dos imágenes de curvas fractales en la Fig. 2 y la Fig. 3: el contorno de 32 segmentos en la Fig. 2, intrincado y que llena el espacio, tiene una dimensión fractal de 1.67, en comparación con el perceptiblemente menos complejo. Curva de Koch en la Fig. 3, que tiene una dimensión fractal de aproximadamente 1.2619.

Gráfico 3 La curva Koch es una curva fractal clásica iterada. Es una construcción teórica que se hace escalando iterativamente un segmento inicial. Como se muestra, cada nuevo segmento es escalado por 1/3 en 4 nuevas piezas colocadas final a fin con 2 piezas medias inclinadas entre las otras dos piezas, de modo que si fueran un triángulo su base sería la longitud de la pieza media, de modo que todo el nuevo segmento se ajuste a la longitud tradicionalmente medida entre los puntos finales del segmento anterior. Mientras que la animación sólo muestra algunas iteraciones, la curva teórica se escala de esta manera infinitamente. Más allá de alrededor de 6 iteraciones en una imagen tan pequeña, el detalle se pierde.

La relación de una dimensión fractal creciente con el llenado del espacio podría interpretarse como que las dimensiones fractales miden la densidad, pero no es así; los dos no están estrictamente correlacionados. En cambio, una dimensión fractal mide la complejidad, un concepto relacionado con ciertas características clave de los fractales: autosimilitud y detalle o irregularidad. Estas características son evidentes en los dos ejemplos de curvas fractales. Ambas son curvas con dimensión topológica de 1, por lo que uno podría esperar poder medir su longitud y derivada de la misma manera que con las curvas ordinarias. Pero no podemos hacer ninguna de estas cosas, porque las curvas fractales tienen una complejidad en forma de autosimilitud y detalle de la que carecen las curvas ordinarias. La autosimilitud radica en la escala infinita, y el detalle en los elementos definitorios de cada conjunto. La longitud entre dos puntos cualesquiera de estas curvas es infinita, sin importar qué tan cerca estén los dos puntos, lo que significa que es imposible aproximar la longitud de dicha curva dividiéndola en muchos segmentos pequeños. Cada pieza más pequeña se compone de un número infinito de segmentos escalados que se ven exactamente como la primera iteración. Estas no son curvas rectificables, lo que significa que no se pueden medir dividiéndolas en muchos segmentos que se aproximen a sus respectivas longitudes. No se pueden caracterizar significativamente encontrando sus longitudes y derivadas. Sin embargo, se pueden determinar sus dimensiones fractales, lo que demuestra que ambas llenan el espacio más que las líneas ordinarias pero menos que las superficies, y permite compararlas en este sentido.

Las dos curvas fractales descritas anteriormente muestran un tipo de autosimilitud que es exacta con una unidad de detalle repetitiva que se visualiza fácilmente. Este tipo de estructura se puede extender a otros espacios (por ejemplo, un fractal que extiende la curva de Koch en un espacio tridimensional tiene una D = 2,5849 teórica). Sin embargo, esta complejidad claramente numerable es solo un ejemplo de la autosimilitud y el detalle que están presentes en los fractales. El ejemplo de la línea costera de Gran Bretaña, por ejemplo, exhibe autosimilitud de un patrón aproximado con escala aproximada. En general, los fractales muestran varios tipos y grados de autosimilitud y detalles que pueden no visualizarse fácilmente. Estos incluyen, como ejemplos, atractores extraños para los cuales el detalle se ha descrito como, en esencia, porciones suaves que se acumulan, el conjunto de Julia, que puede verse como complejos remolinos sobre remolinos, y frecuencias cardíacas, que son patrones de picos ásperos repetidos. y escalado en el tiempo. La complejidad fractal no siempre se puede resolver en unidades de detalle y escala fáciles de entender sin métodos analíticos complejos, pero aún es cuantificable a través de dimensiones fractales.

Historia

Los términos dimensión fractal y fractal fueron acuñados por Mandelbrot en 1975, aproximadamente una década después de publicar su artículo sobre la autosimilitud en la costa de Gran Bretaña. Varias autoridades históricas le atribuyen también la síntesis de siglos de complicados trabajos matemáticos teóricos y de ingeniería y su aplicación de una nueva forma para estudiar geometrías complejas que desafiaban la descripción en los términos lineales habituales. Las primeras raíces de lo que Mandelbrot sintetizó como la dimensión fractal se remontan claramente a los escritos sobre funciones no diferenciables e infinitamente autosimilares, que son importantes en la definición matemática de los fractales, en la época en que se descubrió el cálculo a mediados del siglo XVII. Hubo una pausa en el trabajo publicado sobre tales funciones durante un tiempo después de eso, luego una renovación que comenzó a fines del siglo XIX con la publicación de funciones y conjuntos matemáticos que hoy se denominan fractales canónicos (como los trabajos homónimos de von Koch, Sierpiński, y Julia), pero en el momento de su formulación a menudo se consideraban "monstruos" matemáticos antitéticos. Estos trabajos estuvieron acompañados por quizás el punto más crucial en el desarrollo del concepto de una dimensión fractal a través del trabajo de Hausdorff a principios del siglo XX, quien definió un "fraccional" dimensión que lleva su nombre y se invoca con frecuencia para definir los fractales modernos.

Ver Historia de Fractal para más información

Papel de escalar

Gráfico 4 Nociones tradicionales de geometría para definir escala y dimensión.
1{displaystyle 1}, 12=1{displaystyle 1^{2}{=}1}, 13=1{displaystyle 1^{3}{=}1}
2{displaystyle 2}, 22=4{displaystyle 2^{2}{=}4}, 23=8{displaystyle 2^{3}{=}8}
3{displaystyle 3}, 32=9{displaystyle 3^{2}{=}9}, 33=27{displaystyle 3^{3}{=}27}

El concepto de dimensión fractal descansa en puntos de vista no convencionales de escalado y dimensión. Como ilustra la Figura 4, las nociones tradicionales de la geometría dictan que las formas escalan previsiblemente de acuerdo a ideas intuitivas y familiares sobre el espacio que se contienen dentro, de tal manera que, por ejemplo, midiendo una línea usando primero un palo de medición entonces otro 1/3 su tamaño, dará para el segundo palo una longitud total 3 veces más palos largos que con el primero. Esto también tiene 2 dimensiones. Si uno mide el área de un cuadrado entonces mide de nuevo con una caja de longitud lateral 1/3 del tamaño del original, se encontrará 9 veces más cuadrados que con la primera medida. Tales relaciones de escalamiento familiar se pueden definir matemáticamente por la regla general de escalado en la Ecuación 1, donde la variable N{displaystyle N} representa el número de unidades de medición (adhesivos, cuadrados, etc.), ε ε {displaystyle varepsilon } para el factor de escalado, y D{displaystyle D} para la dimensión fractal:

N=ε ε − − D.{displaystyle {N=varepsilon ^{-D}}

()1)

Esta regla de escalado tipifica reglas convencionales sobre geometría y dimensión – refiriéndose a los ejemplos anteriores, cuantifica que D=1{displaystyle D=1} para líneas porque N=3{displaystyle N=3} cuando ε ε =13{displaystyle varepsilon ={tfrac {1}{3}}, y eso D=2{displaystyle D=2} para cuadrados porque N=9{displaystyle N=9} cuando ε ε =13.{displaystyle varepsilon ={tfrac {1}{3}}

Gráfico 5 Las cuatro primeras iteraciones del copo de nieve Koch, que tiene una dimensión Hausdorff de aproximadamente 1.2619.

La misma regla se aplica a la geometría fractal pero menos intuitiva. Para elaborar, una línea fractal medida al principio para ser una longitud, cuando se remedió utilizando un nuevo palo escalado por 1/3 de la antigüedad puede ser 4 veces más que los palos escalados largos en lugar de los 3 esperados (véase Fig. 5). En este caso, N=4{displaystyle N=4} cuando ε ε =13,{displaystyle varepsilon ={tfrac {1}{3}} y el valor de D{displaystyle D} se puede encontrar reorganizando la Ecuación 1:

logε ε ⁡ ⁡ N=− − D=log⁡ ⁡ Nlog⁡ ⁡ ε ε .{displaystyle {log _{varepsilon } {N}={-D}={frac {log {fn}{log {cHFF} {cHFF} {cHFF} {cHFF} {cHFF} {cHFF}} {cHFF} {cHFF}}} {cHFF}} {ccggccHFF} {ccHFF}}}} {cccccccHFF}} {ccccccccccccHFF} {ccHFF}}}ccccccccccggcccccccccccccccccccccHFF}}}}}}}}}cccccHFF}}cccccc - Sí.

()2)

Es decir, para un fractal descrito por N=4{displaystyle N=4} cuando ε ε =13{displaystyle varepsilon ={tfrac {1}{3}}, como el copo de nieve Koch, D=1.26185...... {displaystyle D=1.26185ldots, un valor no entero que sugiere que el fractal tiene una dimensión no igual al espacio en el que reside.

Nota, las imágenes mostradas en esta página no son fractales verdaderos porque el escalado descrito por D{displaystyle D} no puede continuar más allá del punto de su componente más pequeño, un píxel. Sin embargo, los patrones teóricos que representan las imágenes no tienen piezas discretas como píxel, sino que están compuestos por un número infinito de segmentos infinitamente escalados y de hecho tienen las dimensiones fractales reclamadas.

D no es un descriptor único

Gráfico 6. Dos fractales de ramificación de sistemas L que se hacen produciendo 4 nuevas piezas para cada escalado 1/3 así que tienen la misma teórica D{displaystyle D} como la curva Koch y para la cual la caja empírica cuenta D{displaystyle D} ha sido demostrado con una precisión del 2%.

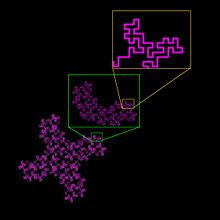
Como es el caso de las dimensiones determinadas para líneas, cuadrados y cubos, las dimensiones fractales son descriptores generales que no definen patrones de manera única. El valor de D para el fractal de Koch discutido anteriormente, por ejemplo, cuantifica la escala inherente del patrón, pero no lo describe de manera única ni proporciona suficiente información para reconstruirlo. Se podrían construir muchas estructuras o patrones fractales que tengan la misma relación de escala pero que sean radicalmente diferentes de la curva de Koch, como se ilustra en la Figura 6.

Para ver ejemplos de cómo se pueden construir patrones fractales, consulte Fractal, triángulo de Sierpinski, conjunto de Mandelbrot, agregación limitada por difusión, L-System.

Estructuras de superficie fractal

El concepto de fractalidad se aplica cada vez más en el campo de la ciencia de superficies, proporcionando un puente entre las características de la superficie y las propiedades funcionales. Numerosos descriptores de superficie se utilizan para interpretar la estructura de superficies nominalmente planas, que a menudo exhiben características afines a sí mismas en múltiples escalas de longitud. La rugosidad media de la superficie, generalmente denotada como R_A, es el descriptor de superficie más comúnmente aplicado, sin embargo, muchos otros descriptores incluyen la pendiente media, la rugosidad cuadrática media (R_RMS) y otros. aplicado regularmente. Sin embargo, se encuentra que muchos fenómenos físicos de la superficie no pueden interpretarse fácilmente con referencia a dichos descriptores, por lo que la dimensión fractal se aplica cada vez más para establecer correlaciones entre la estructura de la superficie en términos de comportamiento de escala y rendimiento. Las dimensiones fractales de las superficies se han empleado para explicar y comprender mejor los fenómenos en las áreas de la mecánica de contacto, el comportamiento de fricción, la resistencia de contacto eléctrico y los óxidos conductores transparentes.

Gráfico 7 Ilustración de creciente fractalidad superficial. Superficies autoafinadas (izquierda) y perfiles superficiales correspondientes (derecha) mostrando una dimensión fractal creciente D_f

Ejemplos

El concepto de dimensión fractal descrito en este artículo es una vista básica de una construcción complicada. Los ejemplos discutidos aquí se eligieron para mayor claridad, y la unidad de escala y las proporciones se conocían con anticipación. En la práctica, sin embargo, las dimensiones fractales se pueden determinar utilizando técnicas que aproximan la escala y el detalle a partir de los límites estimados a partir de líneas de regresión sobre gráficos logarítmicos frente a logarítmicos de tamaño frente a escala. Varias definiciones matemáticas formales de diferentes tipos de dimensión fractal se enumeran a continuación. Aunque para conjuntos compactos con autosimilitud afín exacta todas estas dimensiones coinciden, en general no son equivalentes:

• Dimensión de recuento de caja: D se estima como el exponente de una ley de poder.

D0=limε ε → → 0log⁡ ⁡ N()ε ε )log⁡ ⁡ 1ε ε .{displaystyle D_{0}=lim _{varepsilon to 0}{frac {log N(varepsilon)}{log {frac {1}{varepsilon - Sí.

• Dimensión de la información: D considera cómo la información media necesaria para identificar una escala de caja ocupada con tamaño de caja; p{displaystyle p} es una probabilidad.

D1=limε ε → → 0− − .. log⁡ ⁡ pε ε .. log⁡ ⁡ 1ε ε {displaystyle D_{1}=lim _{varepsilon to 0}{frac {-langle log p_{varepsilon {fnMicroc}{varepsilon }

• Dimensión de correlación: D se basa en M{displaystyle M} como el número de puntos utilizados para generar una representación de un fractal y g_ε, el número de pares de puntos más cercanos que ε entre sí.

D2=limM→ → JUEGO JUEGO limε ε → → 0log⁡ ⁡ ()gε ε /M2)log⁡ ⁡ ε ε {displaystyle D_{2}=lim _{Mto infty }lim _{varepsilon to 0}{frac {log(g_{varepsilon }/M^{2}}{log varepsilon }}}

• Dimensiones generalizadas o Rényi: Las dimensiones de recuento, información y correlación se pueden ver como casos especiales de un espectro continuo de dimensiones generalizadas del orden α, definidos por:

Dα α =limε ε → → 01α α − − 1log⁡ ⁡ ().. ipiα α )log⁡ ⁡ ε ε {displaystyle D_{alpha }=lim _{varepsilon to 0}{frac {frac {1}{alpha -1}log(sum) {fnMicrosoft Sans Serif}} {log varepsilon }

• Dimensión Higuchi

D=dlog⁡ ⁡ ()L()k))dlog⁡ ⁡ ()k){displaystyle D={frac {dlog(L(k)}{dlog(k)}}}}

• Dimensión de Lyapunov
• Dimensiones multifractales: un caso especial de dimensiones Rényi donde el comportamiento de escalado varía en diferentes partes del patrón.
• Uncertainty exponent
• Dimensión Hausdorff: Para cualquier subconjunto S{displaystyle S. de un espacio métrico X{displaystyle X} y d≥ ≥ 0{displaystyle dgeq 0}, el d-dimensional Contenido de Hausdorff de S se define por

0{Bigr }}.}" xmlns="http://www.w3.org/1998/Math/MathML">CHd()S):=inf{}.. irid:hay una cubierta deSpor bolas con radiori■0}.{displaystyle ¿Qué? {Bigl}sum} ¿Por qué? hay una cubierta de }S{text{ por bolas con radio }r_{i} título0{ Más grande.0Bigr}." aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9b29cfc35f60d0afd0c1b16492171b8e03265fee" style="vertical-align: -3.005ex; width:70.903ex; height:6.009ex;"/>

El Dimensión Hausdorff de S se define por

dimH⁡ ⁡ ()X):=inf{}d≥ ≥ 0:CHd()X)=0}.{displaystyle dim _{operatorname {H}(X):=inf{dgeq 0:C_{H} {d}(X)=0}

• Dimensión de embalaje
• Dimensión de Assouad
• Dimensión local conectada

Estimación a partir de datos del mundo real

Muchos fenómenos del mundo real exhiben propiedades fractales limitadas o estadísticas y dimensiones fractales que se han estimado a partir de datos muestreados utilizando técnicas de análisis fractal basadas en computadora. En la práctica, las mediciones de la dimensión fractal se ven afectadas por varios problemas metodológicos y son sensibles al ruido numérico o experimental y las limitaciones en la cantidad de datos. No obstante, el campo está creciendo rápidamente, ya que las dimensiones fractales estimadas para fenómenos estadísticamente similares pueden tener muchas aplicaciones prácticas en varios campos, incluido astronomía, acústica, geología y ciencias de la tierra, diagnóstico por imagen, ecología, procesos electroquimicos, análisis de imagen, biología y medicina, neurociencia, análisis de red, fisiología, física, y Ceros zeta de Riemann. También se ha demostrado que las estimaciones de la dimensión fractal se correlacionan con la complejidad de Lempel-Ziv en conjuntos de datos del mundo real de la psicoacústica y la neurociencia.

Una alternativa a la medición directa es considerar un modelo matemático que se asemeje a la formación de un objeto fractal del mundo real. En este caso, también se puede realizar una validación comparando otras propiedades además de las fractales implícitas en el modelo, con datos medidos. En la física coloidal surgen sistemas compuestos por partículas con varias dimensiones fractales. Para describir estos sistemas, es conveniente hablar de una distribución de dimensiones fractales y, eventualmente, de una evolución temporal de estas últimas: un proceso que está impulsado por una compleja interacción entre agregación y coalescencia.