Dilatación del tiempo

AjustarCompartirImprimirCitar

Diferencia del tiempo medido como explica la teoría de la relatividad

Dilatación del tiempo es la diferencia en el tiempo transcurrido medido por dos relojes, ya sea debido a una velocidad relativa entre ellos (relatividad especial) o debido a una diferencia en el potencial gravitacional entre sus ubicaciones (relatividad general). Cuando no se especifica, la "dilatación del tiempo" generalmente se refiere al efecto debido a la velocidad.

Después de compensar los diferentes retrasos de la señal debido a la distancia cambiante entre un observador y un reloj en movimiento (es decir, el efecto Doppler), el observador medirá el reloj en movimiento como un tictac más lento que un reloj en reposo en el observador' propio marco de referencia. Además, un reloj que se encuentre próximo a un cuerpo masivo (y que por tanto se encuentre a menor potencial gravitatorio) registrará menos tiempo transcurrido que un reloj situado más lejos de dicho cuerpo masivo (y que se encuentre a mayor potencial gravitatorio).

Estas predicciones de la teoría de la relatividad se han confirmado repetidamente mediante experimentos y son de interés práctico, por ejemplo, en el funcionamiento de sistemas de navegación por satélite como GPS y Galileo.

Historia

La dilatación del tiempo por el factor Lorentz fue predicha por varios autores a finales del siglo XX. Joseph Larmor (1897), al menos para electrones que orbitan un núcleo, escribió que los electrones individuales describen partes correspondientes de sus órbitas en tiempos más cortos para el sistema [resto] en la relación: ${textstyle {sqrt {1-{frac {v^{2}}{c^{2}}}}}}$ . Emil Cohn (1904) relacionó específicamente esta fórmula a la velocidad de los relojes. En el contexto de la relatividad especial fue demostrado por Albert Einstein (1905) que este efecto se refiere a la naturaleza del tiempo mismo, y también fue el primero en señalar su reciprocidad o simetría. Posteriormente, Hermann Minkowski (1907) introdujo el concepto de tiempo adecuado que aclaraba aún más el significado de la dilatación temporal.

Dilatación del tiempo causada por una velocidad relativa

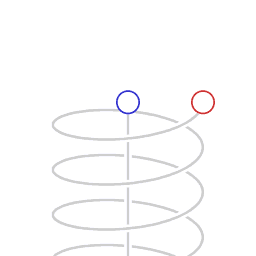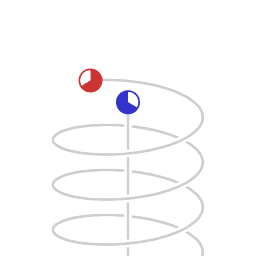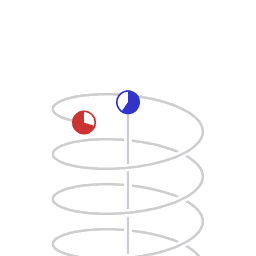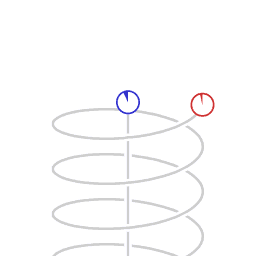
Desde el marco local de referencia del reloj azul, el reloj rojo, al estar en movimiento, se percibe como marca más lento.

La relatividad especial indica que, para un observador en un marco de referencia inercial, un reloj que se mueve en relación con él se medirá con un tictac más lento que un reloj que está en reposo en su marco de referencia. Este caso a veces se llama dilatación del tiempo relativista especial. Cuanto más rápida es la velocidad relativa, mayor es la dilatación del tiempo entre ellos, y el tiempo se detiene a medida que uno se acerca a la velocidad de la luz (299 792 458 m/s).

Teóricamente, la dilatación del tiempo haría posible que los pasajeros de un vehículo en movimiento rápido avanzaran más hacia el futuro en un corto período de tiempo. Para velocidades suficientemente altas, el efecto es dramático. Por ejemplo, un año de viaje podría corresponder a diez años en la Tierra. De hecho, una aceleración constante de 1 g permitiría a los humanos viajar a través de todo el Universo conocido en una vida humana.

Sin embargo, con la tecnología actual que limita severamente la velocidad de los viajes espaciales, las diferencias experimentadas en la práctica son minúsculas: después de 6 meses en la Estación Espacial Internacional (ISS), orbitando la Tierra a una velocidad de aproximadamente 7700 m/s, un astronauta habría envejecido unos 0,005 segundos menos que los de la Tierra. Los cosmonautas Sergei Krikalev y Sergei Avdeyev experimentaron una dilatación del tiempo de unos 20 milisegundos en comparación con el tiempo que pasó en la Tierra.

Inferencia simple

**Izquierda**: Observador en tiempo de descanso 2L/c entre eventos co-locales de generación de señal de luz a A y llegada a A.
**Bien.**: Eventos según un observador que se mueve a la izquierda de la configuración: espejo inferior A cuando la señal se genera a tiempo *t'=*0, espejo superior B cuando la señal se refleja a la vez *t'=D/c*, espejo inferior A cuando la señal regrese a tiempo *t'=2D/c*

La dilatación del tiempo se puede inferir de la constancia observada de la velocidad de la luz en todos los marcos de referencia dictados por el segundo postulado de la relatividad especial.

Esta constancia de la velocidad de la luz significa que, contrariamente a la intuición, las velocidades de los objetos materiales y la luz no son aditivas. No es posible hacer que la velocidad de la luz parezca mayor acercándose o alejándose de la fuente de luz.

Considere entonces, un reloj vertical simple que consta de dos espejos $A$ y $B$ , entre los cuales rebota un pulso de luz. La separación de los espejos es $L$ y el reloj marca una vez cada vez que el pulso de luz golpea el espejo $A$ .

En el cuadro en el que el reloj está en reposo (ver parte izquierda del diagrama), el pulso de luz traza un camino de longitud $2 L$ y el período del reloj es $2 L$ dividido por la velocidad de la luz:

{displaystyle Delta t={frac {2L}{c}}}

Desde el marco de referencia de un observador en movimiento que viaja a la velocidad $v$ en relación con el marco de reposo del reloj (parte derecha del diagrama), el pulso de luz se ve como si trazara un camino en ángulo más largo. Mantener constante la velocidad de la luz para todos los observadores inerciales requiere un alargamiento del período de este reloj desde la perspectiva del observador en movimiento. Es decir, medido en un marco que se mueve en relación con el reloj local, este reloj funcionará más lentamente. La aplicación directa del teorema de Pitágoras conduce a la conocida predicción de la relatividad especial:

El tiempo total para que el pulso de luz siga su camino viene dado por:

{displaystyle Delta t'={frac {2D}{c}}}

La longitud del semirrecorrido se puede calcular en función de cantidades conocidas como:

{displaystyle D={sqrt {left({frac {1}{2}}vDelta t'right)^{2}+L^{2}}}}

Did you mean:

Elimination of the variables <iD and L from these three equations results in:

{displaystyle Delta t'={frac {Delta t}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}

que expresa el hecho de que el período del reloj del observador en movimiento $Delta t'$ es más largo que el período $Delta t$ en el marco del reloj mismo.

Debido a que todos los relojes que tienen un período común en el marco de reposo deben tener un período común cuando se observan desde el marco en movimiento, todos los demás relojes: mecánicos, electrónicos, ópticos (como una versión horizontal idéntica del reloj en el ejemplo) —debería exhibir la misma dilatación del tiempo dependiente de la velocidad.

Reciprocidad

El tiempo UV de un reloj en S es más corto comparado con Ux en S′, y el tiempo UW de un reloj en S′ es más corto comparado con Ux en S

Dado un cierto marco de referencia, y el "estacionario" observador descrito anteriormente, si un segundo observador acompañó al "movimiento" reloj, cada uno de los observadores percibiría el reloj del otro marcando a un ritmo más lento que su propio reloj local, debido a que ambos perciben que el otro es el que está en movimiento relativo a su propio marco de referencia estacionario.

El sentido común dictaría que, si el paso del tiempo se ha ralentizado para un objeto en movimiento, dicho objeto observaría que el tiempo del mundo exterior se acelera correspondientemente. En contra de la intuición, la relatividad especial predice lo contrario. Cuando dos observadores están en movimiento uno respecto del otro, cada uno medirá la desaceleración del reloj del otro, en concordancia con que estén en movimiento en relación con el marco de referencia del observador.

Si bien esto parece contradictorio, una rareza similar ocurre en la vida cotidiana. Si dos personas A y B se observan de lejos, B le parecerá pequeño a A, pero al mismo tiempo A le parecerá pequeño a B. Al estar familiarizado con los efectos de la perspectiva, no hay contradicción ni paradoja en esta situación..

La reciprocidad del fenómeno también conduce a la llamada paradoja de los gemelos, donde se compara el envejecimiento de los gemelos, uno que se queda en la Tierra y el otro que se embarca en un viaje espacial, y donde la reciprocidad sugiere que ambas personas deberían tener el mismo edad cuando se reencuentran. Por el contrario, al final del viaje de ida y vuelta, el gemelo viajero será más joven que el hermano de la Tierra. El dilema planteado por la paradoja, sin embargo, puede explicarse por el hecho de que el gemelo viajero debe acelerar notablemente en al menos tres fases del viaje (inicio, cambio de dirección y final), mientras que el otro solo experimentará una aceleración insignificante, debido a la rotación y revolución de la Tierra. Durante las fases de aceleración del viaje espacial, la dilatación del tiempo no es simétrica.

Pruebas experimentales

Efecto Doppler

El propósito declarado por Ives y Stilwell (1938, 1941) de estos experimentos fue verificar el efecto de dilatación del tiempo, predicho por la teoría de éter Larmor-Lorentz, debido al movimiento a través del éter usando la sugerencia de Einstein de que el efecto Doppler en los rayos del canal proporcionaría un experimento adecuado. Estos experimentos midieron el cambio de Doppler de la radiación emitida a partir de rayos catode, cuando se veía desde directamente en frente y desde directamente detrás. Las frecuencias altas y bajas detectadas no fueron los valores predichos clásicamente: ${displaystyle {frac {f_{0}}{1-v/c}}qquad {text{and}}qquad {frac {f_{0}}{1+v/c}}}$ Las frecuencias altas y bajas de la radiación de las fuentes móviles se midieron como: ${displaystyle {sqrt {frac {1+v/c}{1-v/c}}}f_{0}=gamma left(1+v/cright)f_{0}qquad {text{and}}qquad {sqrt {frac {1-v/c}{1+v/c}}}f_{0}=gamma left(1-v/cright)f_{0},}$ como deducido por Einstein (1905) de la transformación de Lorentz, cuando la fuente está funcionando lentamente por el factor Lorentz.
Hasselkamp, Mondry y Scharmann (1979) midieron el cambio de Doppler desde una fuente que se mueve en ángulos rectos hasta la línea de visión. La relación más general entre las frecuencias de la radiación de las fuentes móviles es dada por: ${displaystyle f_{mathrm {detected} }=f_{mathrm {rest} }{left(1-{frac {v}{c}}cos phi right)/{sqrt {1-{v^{2}}/{c^{2}}}}}}$ como deducido por Einstein (1905). Para φ = 90° ()# φ = 0) esto reduce a f_detectada = f_Descansaγ. Esta menor frecuencia de la fuente móvil se puede atribuir al efecto de dilatación del tiempo y a menudo se llama el efecto transversal Doppler y se predijo por relatividad.
En 2010 se observó dilatación a velocidades de menos de 10 metros por segundo utilizando relojes atómicos ópticos conectados por 75 metros de fibra óptica.

Partículas en movimiento

Es posible comparar las vidas de muones a diferentes velocidades. En el laboratorio se producen muones lentos; y en la atmósfera, los rayos cósmicos introducen muones muy rápidos. Tomando la vida del muón en reposo como el valor de laboratorio de 2.197 μs, la vida de un muón producido por rayos cósmicos que viaja al 98% de la velocidad de la luz es aproximadamente cinco veces más, de acuerdo con las observaciones. Un ejemplo es Rossi y Hall (1941), que comparó la población de muones producidos por rayos cósmicos en la cima de una montaña a la observada a nivel del mar.
La vida de las partículas producidas en los aceleradores de partículas es mayor debido a la dilatación del tiempo. En tales experimentos, la "hora" es el tiempo tomado por procesos que conducen a la decadencia de muones, y estos procesos tienen lugar en el muón en movimiento a su propio "tasa de horas", que es mucho más lento que el reloj de laboratorio. Esto se tiene en cuenta rutinariamente en la física de partículas, y se han realizado muchas mediciones dedicadas. Por ejemplo, en el anillo de almacenamiento de muones en CERN se encontró que la vida de los muones circulando con γ = 29.327 se dilató a 64.378 μs, confirmando la dilatación del tiempo a una precisión de 0,9 ± 0,4 partes por mil.

Tiempo propio y diagrama de Minkowski

Diagrama de Minkowski y paradoja gemela

Reloj C en movimiento relativo entre dos relojes sincronizados A y B. C se reúne A a d, y B en f.

Doble paradoja. Un gemelo tiene que cambiar los marcos, dando lugar a diferentes momentos apropiados en las líneas del mundo del gemelo.

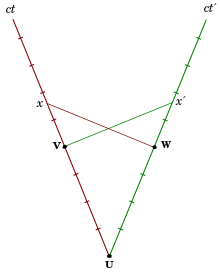
En el diagrama de Minkowski de la primera imagen a la derecha, el reloj C que descansa en el marco inercial S′ se encuentra con el reloj A en d y el reloj B en f (ambos descansan En s). Los tres relojes comienzan a marcar simultáneamente en S. La línea de mundo de A es el eje ct, la línea de mundo de B que se cruza con f es paralela al eje ct, y la línea de mundo de C es el ct′ -eje. Todos los eventos simultáneos con d en S están en el eje x, en S′ en el eje x′.

El tiempo adecuado entre dos eventos se indica mediante un reloj presente en ambos eventos. Es invariante, es decir, en todos los marcos inerciales se acuerda que este tiempo lo indique ese reloj. El intervalo df es, por tanto, el tiempo propio del reloj C, y es más corto con respecto a los tiempos coordenados ef=dg de los relojes B y A en S. A la inversa, también el tiempo propio ef de B es más corto con respecto al tiempo if en S′, porque el evento e ya se midió en S′ en el tiempo i debido a la relatividad de la simultaneidad, mucho antes de que C comenzara a marcar.

De eso se puede ver, que el tiempo propio entre dos eventos indicado por un reloj no acelerado presente en ambos eventos, comparado con el tiempo coordinado sincronizado medido en todos los otros marcos inerciales, es siempre el mínimo intervalo de tiempo entre esos eventos. Sin embargo, el intervalo entre dos eventos también puede corresponder al tiempo propio de los relojes acelerados presentes en ambos eventos. Bajo todos los tiempos propios posibles entre dos eventos, el tiempo propio del reloj no acelerado es máximo, que es la solución a la paradoja de los gemelos.

Derivación y formulación

Además del reloj de luz utilizado anteriormente, la fórmula para la dilatación del tiempo puede derivarse más generalmente de la parte temporal de la transformación de Lorentz. Que haya dos eventos en los que el reloj en movimiento indica ${displaystyle t_{a}}$ y ${displaystyle t_{b}}$ , por lo tanto:

{displaystyle t_{a}^{prime }={frac {t_{a}-{frac {vx_{a}}{c^{2}}}}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}, t_{b}^{prime }={frac {t_{b}-{frac {vx_{b}}{c^{2}}}}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}

Puesto que el reloj permanece en reposo en su marco inercial, sigue ${displaystyle x_{a}=x_{b}}$ , así el intervalo ${displaystyle Delta t^{prime }=t_{b}^{prime }-t_{a}^{prime }}$ es dado por:

Delta t'=gamma ,Delta t={frac {Delta t}{sqrt {1-{frac {v^{2}}{c^{2}}}}}},

donde Δt es el intervalo de tiempo entre dos eventos co-locales (es decir, que ocurren en el mismo lugar) para un observador en algún marco inercial (por ejemplo, garrapatas en sus clock), conocido como el tiempo propio, Δt′ es el intervalo de tiempo entre esos mismos eventos, medido por otro observador, moviéndose inercialmente con velocidad v con respecto al observador anterior, v es la velocidad relativa entre el observador y el reloj en movimiento, c es la velocidad de la luz y el factor de Lorentz (convencionalmente denotado por la letra griega gamma o γ) es:

{displaystyle gamma ={frac {1}{sqrt {1-{frac {v^{2}}{c^{2}}}}}},}

Así, se encuentra que la duración del ciclo de reloj de un reloj en movimiento aumenta: se mide como "funcionando lentamente". El rango de tales variaciones en la vida ordinaria, donde v ≪ c, incluso considerando los viajes espaciales, no son lo suficientemente grandes como para producen efectos de dilatación del tiempo fácilmente detectables y estos efectos tan pequeños que desaparecen pueden ignorarse con seguridad para la mayoría de los propósitos. Como umbral aproximado, la dilatación del tiempo puede volverse importante cuando un objeto se acerca a velocidades del orden de 30 000 km/s (1/10 de la velocidad de la luz).

Movimiento hiperbólico

En la relatividad especial, la dilatación del tiempo se describe de manera más simple en circunstancias en las que la velocidad relativa no cambia. Sin embargo, las ecuaciones de Lorentz permiten calcular el tiempo y el movimiento en el espacio adecuados para el caso simple de una nave espacial que se aplica con una fuerza por unidad de masa, en relación con algún objeto de referencia en movimiento uniforme (es decir, velocidad constante), igual a g durante todo el período de medición.

Sea t el tiempo en un marco inercial llamado posteriormente marco de reposo. Sea x una coordenada espacial, y deje que la dirección de la aceleración constante, así como la velocidad de la nave espacial (en relación con el marco de reposo) sean paralelas a x-eje. Asumiendo que la posición de la nave espacial en el tiempo t = 0 siendo x = 0 y siendo la velocidad v₀ y definiendo la siguiente abreviatura:

{displaystyle gamma _{0}={frac {1}{sqrt {1-v_{0}^{2}/c^{2}}}}}

las siguientes fórmulas son válidas:

Puesto:

{displaystyle x(t)={frac {c^{2}}{g}}left({sqrt {1+{frac {left(gt+v_{0}gamma _{0}right)^{2}}{c^{2}}}}}-gamma _{0}right)}

Velocidad:

{displaystyle v(t)={frac {gt+v_{0}gamma _{0}}{sqrt {1+{frac {left(gt+v_{0}gamma _{0}right)^{2}}{c^{2}}}}}}}

Tiempo propio como función del tiempo coordinado:

{displaystyle tau (t)=tau _{0}+int _{0}^{t}{sqrt {1-left({frac {v(t')}{c}}right)^{2}}}dt'}

En el caso donde v(0) = v₀ = 0 y τ(0) = τ₀ = 0 la integral se puede expresar como una función logarítmica o, de manera equivalente, como una función hiperbólica inversa:

{displaystyle tau (t)={frac {c}{g}}ln left({frac {gt}{c}}+{sqrt {1+left({frac {gt}{c}}right)^{2}}}right)={frac {c}{g}}operatorname {arsinh} left({frac {gt}{c}}right)}

Como funciones del tiempo adecuado $tau$ de la nave, las siguientes fórmulas:

Puesto:

{displaystyle x(tau)={frac {c^{2}}{g}}left(cosh {frac {gtau }{c}}-1right)}

Velocidad:

{displaystyle v(tau)=ctanh {frac {gtau }{c}}}

Coordinar el tiempo en función del tiempo propio:

{displaystyle t(tau)={frac {c}{g}}sinh {frac {gtau }{c}}}

Hipótesis del reloj

El hipótesis del reloj es la suposición de que la velocidad a la que un reloj se ve afectado por la dilatación del tiempo no depende de su aceleración sino sólo de su velocidad instantánea. Esto equivale a afirmar que un reloj se mueve por un camino $P$ mide el tiempo adecuado, definido por:

{displaystyle tau =int _{P}{sqrt {dt^{2}-dx^{2}/c^{2}-dy^{2}/c^{2}-dz^{2}/c^{2}}}}

La hipótesis del reloj se incluyó implícitamente (pero no explícitamente) en la formulación original de 1905 de la relatividad especial de Einstein. Desde entonces, se ha convertido en una suposición estándar y generalmente se incluye en los axiomas de la relatividad especial, especialmente a la luz de la verificación experimental hasta aceleraciones muy altas en aceleradores de partículas.

Dilatación del tiempo causada por la gravedad o la aceleración

La dilatación del tiempo gravitacional es experimentada por un observador que, a cierta altitud dentro de un pozo de potencial gravitacional, descubre que sus relojes locales miden menos tiempo transcurrido que los relojes idénticos situados a mayor altitud (y que, por lo tanto, tienen un potencial gravitacional más alto).

La dilatación del tiempo gravitacional está en juego, p. para los astronautas de la ISS. Mientras que los astronautas' la velocidad relativa ralentiza su tiempo, la reducida influencia gravitacional en su ubicación lo acelera, aunque en menor grado. Además, en teoría, el tiempo de un escalador pasa un poco más rápido en la cima de una montaña en comparación con las personas al nivel del mar. También se ha calculado que, debido a la dilatación del tiempo, el núcleo de la Tierra es 2,5 años más joven que la corteza. "Un reloj usado para cronometrar una rotación completa de la Tierra medirá el día como aproximadamente 10 ns/día más largo por cada kilómetro de altitud sobre el geoide de referencia." Viajar a regiones del espacio donde se está produciendo una dilatación del tiempo gravitacional extrema, como cerca (pero no más allá del horizonte de eventos) de un agujero negro, podría producir resultados de cambio de tiempo análogos a los de los viajes espaciales a la velocidad de la luz.

Al contrario de la dilatación del tiempo por velocidad, en la que ambos observadores miden que el otro envejece más lentamente (un efecto recíproco), la dilatación del tiempo gravitacional no es recíproca. Esto significa que con la dilatación del tiempo gravitacional, ambos observadores están de acuerdo en que el reloj más cercano al centro del campo gravitatorio es más lento y están de acuerdo en la relación de la diferencia.

Pruebas experimentales

En 1959, Robert Pound y Glen A. Rebka midieron el pequeño cambio gravitacional en la frecuencia de la luz emitida a una altura inferior, donde el campo gravitacional de la Tierra es relativamente más intenso. Los resultados fueron dentro del 10% de las predicciones de la relatividad general. En 1964, Pound y J. L. Snider midieron un resultado dentro del 1% del valor predicho por la dilatación del tiempo gravitacional. (Véase Pound–Rebka experiment)
En 2010, la dilatación de tiempo gravitacional se midió en la superficie de la Tierra con una diferencia de altura de sólo un metro, utilizando relojes atómicos ópticos.

Efecto combinado de la velocidad y la dilatación del tiempo gravitacional

El cronometraje de alta precisión, el seguimiento de satélites en órbita terrestre baja y el cronometraje de púlsares son aplicaciones que requieren la consideración de los efectos combinados de la masa y el movimiento para producir la dilatación del tiempo. Los ejemplos prácticos incluyen el estándar de tiempo atómico internacional y su relación con el estándar de tiempo de coordenadas baricéntricas utilizado para objetos interplanetarios.

Los efectos de dilatación de tiempo relativos para el sistema solar y la Tierra pueden ser modelados muy precisamente por la solución Schwarzschild a las ecuaciones de campo de Einstein. En la métrica Schwarzschild, el intervalo ${displaystyle dt_{text{E}}}$ es dado por:

{displaystyle dt_{text{E}}^{2}=left(1-{frac {2GM_{text{i}}}{r_{text{i}}c^{2}}}right)dt_{text{c}}^{2}-left(1-{frac {2GM_{text{i}}}{r_{text{i}}c^{2}}}right)^{-1}{frac {dx^{2}+dy^{2}+dz^{2}}{c^{2}}}}

donde:

${displaystyle dt_{text{E}}}$ es un pequeño aumento de tiempo adecuado ${displaystyle t_{text{E}}}$ (un intervalo que se puede registrar en un reloj atómico)
${displaystyle dt_{text{c}}}$ es un pequeño aumento en la coordenadas ${displaystyle t_{text{c}}}$ (tiempo coordinado),
${displaystyle dx,dy,dz}$ son pequeños incrementos en las tres coordenadas $x, y, z$ de la posición del reloj,
${displaystyle {frac {-GM_{i}}{r_{i}}}}$ representa la suma de los potenciales gravitatorios Newtonianos debido a las masas del vecindario, basado en sus distancias $r_{i}$ del reloj. Esta suma incluye cualquier potencial de marea.

La velocidad coordinada del reloj está dada por:

{displaystyle v^{2}={frac {dx^{2}+dy^{2}+dz^{2}}{dt_{text{c}}^{2}}}}

El tiempo de coordenadas $t_c$ es el tiempo que se leería en un hipotético reloj "coordinado" situado infinitamente lejos de todas las masas gravitacionales ( $U=0$ ), y estacionario en el sistema de coordenadas ( $v=0$ ). La relación exacta entre la tasa de tiempo adecuado y la tasa de tiempo de coordenadas para un reloj con un componente radial de velocidad es:

{displaystyle {frac {dt_{text{E}}}{dt_{text{c}}}}={sqrt {1+{frac {2U}{c^{2}}}-{frac {v^{2}}{c^{2}}}+left({frac {c^{2}}{2U}}+1right)^{-1}{frac {{v_{shortparallel }}^{2}}{c^{2}}}}}={sqrt {1-left(beta ^{2}+beta _{e}^{2}+{frac {beta _{shortparallel }^{2}beta _{e}^{2}}{1-beta _{e}^{2}}}right)}}}

donde:

${displaystyle v_{shortparallel }}$ es la velocidad radial,
${displaystyle v_{e}={sqrt {frac {2GM_{i}}{r_{i}}}}}$ es la velocidad de escape,
$beta = v/c$ , ${displaystyle beta _{e}=v_{e}/c}$ y ${displaystyle beta _{shortparallel }=v_{shortparallel }/c}$ son velocidades como porcentaje de velocidad de luz c,
${displaystyle U={frac {-GM_{i}}{r_{i}}}}$ es el potencial newtoniano; por lo tanto ${displaystyle -U}$ equivale a la mitad del cuadrado de la velocidad de escape.

La ecuación anterior es exacta bajo los supuestos de la solución Schwarzschild. Se reduce a la ecuación de dilatación de tiempo de velocidad en la presencia de movimiento y ausencia de gravedad, es decir. ${displaystyle beta _{e}=0}$ . Reduce a la ecuación de dilatación de tiempo gravitacional en ausencia de movimiento y presencia de gravedad, es decir. ${displaystyle beta =0=beta _{shortparallel }}$ .

Pruebas experimentales

Hafele y Keating, en 1971, volaron relojes atómicos de cesio al este y al oeste alrededor de la Tierra en aerolíneas comerciales, para comparar el tiempo transcurrido contra el de un reloj que permaneció en el Observatorio Naval estadounidense. Dos efectos opuestos entraron en juego. Se esperaba que los relojes envejecieran con más rapidez (show a larger elapsed time) que el reloj de referencia ya que estaban en un potencial gravitacional superior (weaker) para la mayoría del viaje (c.f. Pound-Rebka experiment). Pero también, en contraste, se esperaba que los relojes móviles aumentaran más lentamente debido a la velocidad de su viaje. De las trayectorias de vuelo reales de cada viaje, la teoría predijo que los relojes voladores, comparados con los relojes de referencia en el Observatorio Naval de Estados Unidos, deberían haber perdido 40±23 nanosegundos durante el viaje hacia el este y deberían haber ganado 275±21 nanosegundos durante el viaje hacia el oeste. En relación con la escala de tiempo atómica del Observatorio Naval de Estados Unidos, los relojes voladores perdieron 59±10 nanosegundos durante el viaje hacia el este y obtuvieron 273±7 nanosegundos durante el viaje hacia el oeste (donde las barras de error representan la desviación estándar). En 2005, el Laboratorio Nacional de Física del Reino Unido informó de su limitada replicación de este experimento. El experimento NPL difiere del original en que los relojes de cesio fueron enviados en un viaje más corto (Londres-Washington, D.C. retorno), pero los relojes fueron más precisos. Los resultados reportados están dentro del 4% de las predicciones de relatividad, dentro de la incertidumbre de las mediciones.
El Sistema Mundial de Posicionamiento puede considerarse un experimento de funcionamiento continuo en la relatividad especial y general. Los relojes en órbita son corregidos para efectos especiales y generales de dilatación de tiempo relativista como se describe anteriormente, de modo que (como se observa desde la superficie de la Tierra) corren al mismo ritmo que los relojes en la superficie de la Tierra.

En la cultura popular

La velocidad y la dilatación del tiempo gravitacional han sido objeto de trabajos de ciencia ficción en una variedad de medios. Algunos ejemplos en el cine son las películas Interstellar y El planeta de los simios. En Interstellar, un punto clave de la trama involucra un planeta, que está cerca de un agujero negro en rotación y en cuya superficie una hora equivale a siete años en la Tierra debido a la dilatación del tiempo. El físico Kip Thorne colaboró en la realización de la película y explicó sus conceptos científicos en el libro The Science of Interstellar.

La dilatación del tiempo se usó en los episodios de Doctor Who "World Enough and Time" y 'The Doctor Falls', que tienen lugar en una nave espacial en las cercanías de un agujero negro. Debido a la inmensa atracción gravitatoria del agujero negro y la longitud de la nave (400 millas), el tiempo se mueve más rápido en un extremo que en el otro. Cuando el compañero del Doctor, Bill, es llevado al otro extremo del barco, ella espera años a que él la rescate; en su tiempo, solo pasan minutos. Además, la dilatación permite a los Cybermen evolucionar a un ritmo "más rápido" velocidad que la vista anteriormente en el programa.

Tau Zero, una novela de Poul Anderson, es un ejemplo temprano del concepto en la literatura de ciencia ficción. En la novela, una nave espacial utiliza un estatorreactor Bussard para acelerar a velocidades lo suficientemente altas como para que la tripulación pase cinco años a bordo, pero pasan treinta y tres años en la Tierra antes de llegar a su destino. Anderson explica la dilatación del tiempo de la velocidad en términos del factor tau, que disminuye cada vez más cerca de cero a medida que la nave se acerca a la velocidad de la luz, de ahí el título de la novela. Debido a un accidente, la tripulación no puede dejar de acelerar la nave espacial, lo que provoca una dilatación del tiempo tan extrema que la tripulación experimenta el Big Crunch al final del universo. Otros ejemplos en la literatura, como Rocannon's World y The Forever War, hacen uso similar de la dilatación del tiempo relativista como un recurso literario científicamente plausible para hacer que ciertos personajes envejezcan. más lento que el resto del universo.

Contenido relacionado

Más resultados...

Dilatación del tiempo

Historia

Dilatación del tiempo causada por una velocidad relativa

Inferencia simple

Reciprocidad

Pruebas experimentales

Efecto Doppler

Partículas en movimiento

Tiempo propio y diagrama de Minkowski

Derivación y formulación

Movimiento hiperbólico

Hipótesis del reloj

Dilatación del tiempo causada por la gravedad o la aceleración

Pruebas experimentales

Efecto combinado de la velocidad y la dilatación del tiempo gravitacional

Pruebas experimentales

En la cultura popular

Contenido relacionado

Alcanfor

Relación de aspecto (aeronáutica)

Universidad de Oulu