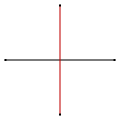
Digón

En geometría, un bigón, dígono o un 2-gono es un polígono con dos lados (aristas) y dos vértices. Su construcción es degenerada en un plano euclidiano porque o bien los dos lados coincidirían o bien uno o ambos tendrían que ser curvos; sin embargo, se puede visualizar fácilmente en el espacio elíptico. También se puede ver como una representación de un gráfico con dos vértices, véase "Polígono generalizado".

Un dígono regular tiene ambos ángulos y ambos lados iguales y se representa con el símbolo de Schläfli {2}. Puede construirse sobre una esfera como un par de arcos de 180 grados que conectan puntos antípodas, cuando forma una luna.

El dígon es el politopo abstracto más simple de rango 2.

Un dígono truncado, t{2} es un cuadrado, {4}. Un dígono alternado, h{2} es un monógono, {1}.

El dígon puede tener una de dos representaciones visuales si se lo coloca en el espacio euclidiano.

Una representación es degenerada y visualmente aparece como una doble cobertura de un segmento de línea. Esta forma, que aparece cuando la distancia mínima entre los dos bordes es 0, surge en varias situaciones. Esta forma de doble cobertura se utiliza a veces para definir casos degenerados de algunos otros politopos; por ejemplo, un tetraedro regular puede verse como un antiprisma formado por dicho digón. Puede derivarse de la alternancia de un cuadrado (h{4}), ya que requiere que dos vértices opuestos de dicho cuadrado estén conectados. Cuando se alternan politopos de dimensiones superiores que involucran cuadrados u otras figuras tetragonales, estos digones generalmente se descartan y se consideran bordes simples.

Una segunda representación visual, infinita en tamaño, es como dos líneas paralelas que se extienden hasta (y se encuentran proyectivamente en; es decir, que tienen vértices en) el infinito, que surge cuando la distancia más corta entre los dos bordes es mayor que cero. Esta forma surge en la representación de algunos politopos degenerados, un ejemplo notable es el hosoedro apeirogonal, el límite de un hosoedro esférico general en el infinito, compuesto por un número infinito de digones que se encuentran en dos puntos antípodas en el infinito. Sin embargo, como los vértices de estos digones están en el infinito y, por lo tanto, no están limitados por segmentos de línea cerrados, esta teselación no suele considerarse una teselación regular adicional del plano euclidiano, incluso cuando su teselación apeirogonal dual de orden 2 (diedro infinito) sí lo es.

• 
  Un compuesto de dos "segmento de línea" digones, como las dos posibles alternaciones de un cuadrado (nota el arreglo del vértice).
• 
  El apeirogonal hosohedron, que contiene digones infinitamente estrechos.

Todo dígono de lados rectos es regular aunque sea degenerado, porque sus dos aristas tienen la misma longitud y sus dos ángulos son iguales (ambos de cero grados). Por lo tanto, el dígono regular es un polígono construible.

Algunas definiciones de polígono no consideran que el dígono sea un polígono propio debido a su degeneración en el caso euclidiano.

Un dígono como cara de un poliedro es degenerado porque es un polígono degenerado. Pero a veces puede tener una existencia topológica útil en la transformación de poliedros.

Una luna esférica es un dígono cuyos dos vértices son puntos antípodas en la esfera.

Un poliedro esférico construido a partir de dichos digones se llama hosoedro.

• 
  Una luna en la esfera.
• 
  Seis caras de digon en un hosohedro hexagonal regular.

Los digones (bigones) pueden utilizarse para construir y analizar diversas estructuras topológicas, como las estructuras de incidencia.

• Monogon
• Demihypercube
• Decagon

• Herbert Busemann, La geometría de la geodésica. New York, Academic Press, 1955
• Coxeter, Polytopes regulares (tercera edición), Dover Publications Inc, 1973 ISBN 0-486-61480-8
• Weisstein, Eric W. "Digon". MathWorld.
• A.B. Ivanov (2001) [1994], "Digon", Enciclopedia de Matemáticas, EMS Prensa

• Medios relacionados con Digons en Wikimedia Commons