Diferencia en diferencias

Diferencia en las diferencias ()DID o DD) es una técnica estadística utilizada en la investigación econométrica y cuantitativa en las ciencias sociales que intenta imitar un diseño de investigación experimental utilizando datos de estudio observacional, estudiando el efecto diferencial de un tratamiento en un 'grupo de tratamiento' contra un 'grupo de control' en un experimento natural. Calcula el efecto de un tratamiento (es decir, una variable explicativa o una variable independiente) en un resultado (es decir, una variable de respuesta o variable dependiente) comparando el cambio promedio con el tiempo en la variable de resultado para el grupo de tratamiento con el cambio promedio con el tiempo para el grupo de control. Aunque se pretende mitigar los efectos de factores extraneosos y sesgo de selección, dependiendo de cómo se elija el grupo de tratamiento, este método puede estar sujeto a ciertos sesgos (por ejemplo, regresión media, causalidad inversa y sesgo variable omitido).

A diferencia de una estimación de series temporales del efecto del tratamiento en los sujetos (que analiza las diferencias a lo largo del tiempo) o una estimación transversal del efecto del tratamiento (que mide la diferencia entre los grupos de tratamiento y control), la diferencia en diferencias utiliza datos de panel para medir las diferencias, entre el grupo de tratamiento y de control, de los cambios en la variable de resultado que ocurren a lo largo del tiempo.

Definición general

La diferencia en las diferencias requiere datos medidos de un grupo de tratamiento y un grupo de control en dos o más períodos de tiempo diferentes, específicamente al menos un período de tiempo antes del "tratamiento" y al menos un período de tiempo después del "tratamiento". En el ejemplo ilustrado, el resultado en el grupo de tratamiento está representado por la línea P y el resultado en el grupo de control está representado por la línea S. La variable de resultado (dependiente) en ambos grupos se mide a la hora 1, antes de que ambos grupos hayan recibido el tratamiento (es decir, la variable independiente o explicativa), representada por los puntos P₁ y S₁. El grupo de tratamiento recibe o experimenta el tratamiento y ambos grupos se miden de nuevo a la vez 2. No toda la diferencia entre los grupos de tratamiento y control a la hora 2 (es decir, la diferencia entre P₂ y S₂) se puede explicar como un efecto del tratamiento, porque el grupo de tratamiento y el grupo de control no comenzó en el mismo punto a la vez 1. DID, por lo tanto, calcula la diferencia "normal" en la variable de resultado entre los dos grupos (la diferencia que todavía existiría si ningún grupo experimentara el tratamiento), representado por la línea punteada Q. (Nota que la pendiente de P₁ a Q es lo mismo que la pendiente desde S₁ a S₂) El efecto del tratamiento es la diferencia entre el resultado observado (P)₂) y el resultado "normal" (la diferencia entre P₂ y Q).

Definición formal

Considere el modelo

${\displaystyle Y... ¿Qué? I(\dots)+\varepsilon _{it}$

Donde ${\displaystyle y_{it}$ es la variable dependiente para el individuo ${\displaystyle i}$ y tiempo ${\displaystyle t}$, ${\displaystyle s(i)}$ es el grupo al que ${\displaystyle i}$ pertenece (es decir, el tratamiento o el grupo de control) y ${\displaystyle I(\dots)}$ es corto para la variable dummy igual a 1 cuando el evento descrito en ${\displaystyle (\dots)}$ es verdad, y 0 de lo contrario. En la trama del tiempo versus ${\displaystyle Sí.$ por grupo, ${\displaystyle \gamma _{s}$ es la interceptación vertical del gráfico para ${\displaystyle s}$, y ${\displaystyle \lambda ¿Qué?$ es la tendencia de tiempo compartida por ambos grupos según la hipótesis de tendencia paralela (véase Assumptions below). ${\displaystyle \delta }$ es el efecto del tratamiento, y ${\displaystyle \varepsilon _{it}$ es el término residual.

Considere el promedio de la variable dependiente y los indicadores ficticios por grupo y tiempo:

${\displaystyle {\begin{aligned}n_{s} limit={\text{ number of individuals in group }s\\\\{\overline {y}_{st} {\fnMicroc} {1}{n_{s}}\sum ¿Qué? I(s(i)~=~s),\\\{\overline {\gamma} ### {\fnMicroc {1}{n_{s}}\sum ¿Por qué? I(s(i)~=~s)~=~\gamma ¿Qué? {\fnMicrode }_{st={\frac {1}{n_{s}}\sum ¿Por qué? ¿Qué? {1}{n_{s}}\sum ¿Por qué? I(s(i)~=~s)~=~I(s~=~{\text{ treatment, }t{\text{ in after period}}}),\{\s\overline {\varepsilon }_{st={\frac {1}{n_{s}}\sum ¿Por qué?$

y suponer para la simplicidad que ${\displaystyle s=1,2}$ y ${\displaystyle t=1,2}$. Note que ${\displaystyle D_{st}$ no es aleatorio; solo codifica cómo se etiquetan los grupos y los períodos. Entonces...

${\displaystyle {\begin{aligned} {y}_{11}-{\overline {y}_{12}-({\overline) {y}_{21}-{\overline {y}_{22}\[6pt]={}{\big [\gamma _{1}+\lambda _{1}+\delta D_{11}+{\overline {\varepsilon }_{11})-(\gamma) _{1}+\lambda _{2}+\delta D_{12}+{\overline {\varepsilon {\fnMicrosoft Sans Serif}\\\fnMicrosoft Sans Serif} {}-{\big [\gamma _{2}+\lambda _{1}+\delta D_{21}+{\overline {\varepsilon }_{21}-(\gamma) _{2}+\lambda _{2}+\delta D_{22}+{\overline {\varepsilon }_{22} {\big ###\[6pt]={} {\delta (D_{11}-D_{12})+\delta (D_{22}-D_{21})+{\overline {\varepsilon }_{11}-{\overline {\varepsilon }_{12}+{\overline {\varepsilon }_{22}-{\overline {\varepsilon }_{21}.$

El supuesto de exogeneidad estricta implica entonces que

${\displaystyle \operatorname {E} \left[{\overline] {y}_{11}-{\overline {y}_{12}-({\overline) {y}_{21}-{\overline {y}_{22}\right]~=~\delta (D_{11}-D_{12})+\delta (D_{22}-D_{21}). }$

Sin pérdida de generalidad, asuma que ${\displaystyle s=2}$ es el grupo de tratamiento, y ${\displaystyle t=2}$ es el período posterior, entonces ${\displaystyle D_{22}=1}$ y ${\displaystyle D_{11}=D_{12}=D_{21}=0}$, dando el estimador DID

${\displaystyle {\hat {\delta ♪♪♪♪♪ {y}_{11}-{\overline {y}_{12}-({\overline) {y}_{21}-{\fn}_{22}}$

que se puede interpretar como el efecto del tratamiento indicado por el ${\displaystyle D_{st}$. A continuación se muestra cómo este estimador se puede leer como un coeficiente en una regresión mínima ordinaria. El modelo descrito en esta sección es sobre-parametrizado; para remediar que, uno de los coeficientes de las variables muñecos se puede establecer a 0, por ejemplo, podemos establecer ${\displaystyle \gamma _{1}=0}$.

Suposiciones

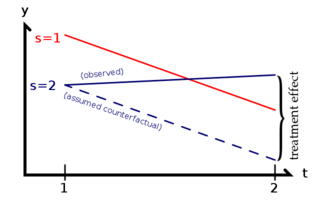
Todas las suposiciones del modelo OLS se aplican por igual al DID. Además, el DID requiere un Hipótesis de tendencia paralela. La hipótesis de tendencia paralela dice que ${\displaystyle \lambda ¿Qué? ¿Qué?$ son los mismos en ambos ${\displaystyle s=1}$ y ${\displaystyle s=2}$. Dado que la definición formal anterior representa con precisión la realidad, esta suposición se sostiene automáticamente. Sin embargo, un modelo con ${\displaystyle \lambda ¿Qué? _{22}-\lambda _{21}\neq \lambda _{12}-\lambda _{11}$ puede ser más realista. A fin de aumentar la probabilidad de que la hipótesis de tendencia paralela tenga lugar, a menudo se combina un enfoque de diferencia en diferencias con la combinación de coincidencias. Esto implica unidades de 'Matching' conocidas 'tratamiento' con unidades de control antifactual simuladas: unidades características equivalentes que no recibieron tratamiento. Al definir el Resultado Variable como una diferencia temporal (cambio de resultado observado entre los períodos de pre- y post-tratamiento), y Combinando múltiples unidades en una gran muestra sobre la base de historias similares de pre-tratamiento, el ATE resultante (es decir, el ATT: Efecto promedio del tratamiento para el tratado) proporciona una estimación robusta de diferencias en las diferencias de los efectos del tratamiento. Esto sirve a dos fines estadísticos: en primer lugar, condicionados a covariaciones previas al tratamiento, es probable que se sostenga la hipótesis de tendencias paralelas; y en segundo lugar, este enfoque reduce la dependencia de los supuestos de ignorancia asociados necesarios para la inferencia válida.

Como se ilustra a la derecha, el efecto del tratamiento es la diferencia entre el valor observado de y y lo que habría sido el valor de y con tendencias paralelas, si hubiera habido No ha habido tratamiento. El Aquiles' El talón del TID es cuando algo distinto al tratamiento cambia en un grupo pero no en el otro al mismo tiempo que el tratamiento, lo que implica una violación del supuesto de tendencia paralela.

Para garantizar la precisión de la estimación del DID, se supone que la composición de los individuos de los dos grupos permanece sin cambios a lo largo del tiempo. Cuando se utiliza un modelo DID, se deben considerar y abordar varios problemas que pueden comprometer los resultados, como la autocorrelación y las caídas de Ashenfelter.

Implementación

El método DID se puede implementar de acuerdo con la siguiente tabla, donde la celda inferior derecha es el estimador DID.

${\displaystyle y_{st}$	${\displaystyle s=2}$	${\displaystyle s=1}$	Diferencia
${\displaystyle t=2}$	${\displaystyle y_{22}$	${\displaystyle y_{12}$	${\displaystyle Y...$
${\displaystyle t=1}$	${\displaystyle y_{21}$	${\displaystyle y_{11}$	${\displaystyle Y...$
Cambio	${\displaystyle Y...$	${\displaystyle Y...$	${\displaystyle (y_{11}-y_{21}-(y_{12}-y_{22}}$

Al ejecutar un análisis de regresión se obtiene el mismo resultado. Considere el modelo OLS

${\displaystyle Y... ¿Qué? ################################################################################################################################################################################################################################################################ S+beta ¿Por qué?$

Donde ${\displaystyle T}$ es una variable mutilada para el período, igual a ${\displaystyle 1}$ cuando ${\displaystyle t=2}$, y ${\displaystyle S.$ es una variable sombría para la membresía de grupo, igual a ${\displaystyle 1}$ cuando ${\displaystyle s=2}$. La variable compuesta ${\displaystyle (T\cdot S)}$ es una variable dummy que indica cuándo ${\displaystyle S=T=1}$. Aunque no se muestra rigurosamente aquí, esta es una adecuada parametrización de la definición formal modelo, además, resulta que los promedios de grupo y período en esa sección se refieren a las estimaciones del parámetro modelo como sigue:

${\displaystyle {\begin{aligned}{\hat {\beta} {\fnMicrosoft Sans Serif}\[8pt]{\beta] {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}(y\mid T=0,~S=0)\[8pt]{\hat {\beta }_{3} {={\big {\fnMicrosoft} T=1,~S=1)-{\widehat {E}(y\mid T=0,~S=1) {\big]}\\\\\\qquad {\fnK} {\fnMicrosoft} T=1,~S=0)-{\widehat {E}(y\mid T=0,~S=0){\big]},\end{aligned}}$

Donde ${\displaystyle {\widehat {E}(\dots \mid \dots)}$ representa promedios condicionales calculados en la muestra, por ejemplo, ${\displaystyle T=1}$ es el indicador para el período posterior, ${\displaystyle S=0}$ es un indicador para el grupo de control. Note que ${\displaystyle {\hat {\beta }_{1}$ es una estimación del contrafactual más que el impacto del grupo de control. El grupo de control se utiliza a menudo como un proxy para el contrafactual (ver, método de control sintético para una comprensión más profunda de este punto). Por ahí, ${\displaystyle {\hat {\beta }_{1}$ se puede interpretar como el impacto tanto del grupo de control como del contrafactual de la intervención (tratamiento). Análogamente, ${\displaystyle {\hat {\beta }_{2}$, debido al supuesto paralelo de tendencia, es también la misma diferencia entre el grupo de tratamiento y control en ${\displaystyle T=1}$. Las descripciones anteriores no deben interpretarse para implicar el efecto (promedio) de sólo el grupo de control, para ${\displaystyle {\hat {\beta }_{1}$, o sólo la diferencia de los grupos de tratamiento y control en el pre-período, para ${\displaystyle {\hat {\beta }_{2}$. Como en Card y Krueger, a continuación, una primera (tiempo) diferencia de la variable de resultado ${\displaystyle (\Delta Y_{i}=Y_{i,1}-Y_{i,0}$ elimina la necesidad de temporización (es decir, ${\displaystyle {\hat {\beta }_{1}$) para formar una estimación imparcial de ${\displaystyle {\hat {\beta }_{3}$, implicando que ${\displaystyle {\hat {\beta }_{1}$ no está realmente condicionado al grupo de tratamiento o control. De manera consistente, una diferencia entre los grupos de tratamiento y control eliminaría la necesidad de diferenciales de tratamiento (es decir, ${\displaystyle {\hat {\beta }_{2}$) para formar una estimación imparcial de ${\displaystyle {\hat {\beta }_{3}$. Este matiz es importante para entender cuando el usuario cree (debilidad) que existen violaciones de pre-trend paralelas o en el caso de violaciones de los supuestos de aproximación contrafactual apropiados dada la existencia de choques no comunes o acontecimientos confusos. Para ver la relación entre esta notación y la sección anterior, considere como por encima sólo una observación por período de tiempo para cada grupo, entonces

${\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f} {\fnMicrosoft ] {\f} {\fnMicrosoft} {\f} {\f} {\f}} {\f}} {\fnMicrom}} {\fnMicrom} {\fnMicrom}} {\f}}} {\fnMicrom} {\fnMicrom}}}}}}}\fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMicrosoft}\fnMicrosoft}}\fnMinMinMicrosoft}\fnMicrosoft}\fnMicrosoft} {\fnMicro ################################################################################################################################################################################################################################################################ {\fnMicrosoft Sans Serif}\[3pt]\\\\fnMicrosoft Sans Serif {y} {\text{12}\end{aligned}}$

y así sucesivamente para otros valores ${\displaystyle T}$ y ${\displaystyle S.$, que equivale a

${\displaystyle {\hat {\beta - Sí.$

Pero esta es la expresión para el efecto del tratamiento que se dio en la definición formal y en la tabla anterior.

Ejemplo de Card y Krueger (1994)

El artículo de Card y Krueger sobre el salario mínimo en Nueva Jersey, publicado en 1994, se considera uno de los estudios DID más famosos; Posteriormente, Card recibió el Premio Nobel de Ciencias Económicas de 2021 en parte por este trabajo y otros relacionados. Card y Krueger compararon el empleo en el sector de comida rápida en Nueva Jersey y en Pensilvania, en febrero de 1992 y en noviembre de 1992, después de que el salario mínimo de Nueva Jersey aumentara de $4,25 a $5,05 en abril de 1992. Observando un cambio en el empleo en Nueva Jersey Sólo Jersey, antes y después del tratamiento, no controlaría variables omitidas como el clima y las condiciones macroeconómicas de la región. Al incluir Pensilvania como control en un modelo de diferencias en diferencias, se controla implícitamente cualquier sesgo causado por variables comunes a Nueva Jersey y Pensilvania, incluso cuando estas variables no se observan. Suponiendo que Nueva Jersey y Pensilvania tengan tendencias paralelas a lo largo del tiempo, el cambio en el empleo de Pensilvania puede interpretarse como el cambio que habría experimentado Nueva Jersey si no hubieran aumentado el salario mínimo, y viceversa. La evidencia sugirió que el aumento del salario mínimo no indujo una disminución del empleo en Nueva Jersey, contrariamente a lo que sugeriría alguna teoría económica. La siguiente tabla muestra Tarjeta y datos. Estimaciones de Krueger del efecto del tratamiento sobre el empleo, medido como FTE (o equivalentes a tiempo completo). Card y Krueger estiman que el aumento del salario mínimo de $0,80 en Nueva Jersey condujo a un aumento de 2,75 FTE en el empleo.

Un ejemplo de aplicación de software de esta investigación se encuentra en el comando Stata -diff- escrito por Juan Miguel Villa.