Diedro
Un diedro es un tipo de poliedro formado por dos caras poligonales que comparten el mismo conjunto de n aristas. En el espacio euclidiano tridimensional, es degenerado si sus caras son planas, mientras que en el espacio esférico tridimensional, un diedro con caras planas puede considerarse como una lente, un ejemplo de lo cual es el dominio fundamental de un espacio de lentes L(p,q). Los diedros también se han denominado biedros, poliedros planos o polígonos doblemente cubiertos.
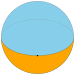
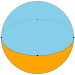
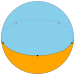
Como teselación esférica, un diedro puede existir como forma no degenerada, con dos caras de n lados que cubren la esfera, cada cara es un hemisferio y los vértices están en un círculo máximo. Es regular si los vértices están espaciados de manera uniforme.
El dual de un diedro n-gonal es un hosoedro n-gonal, donde n caras del diedro comparten dos vértices.
Como poliedro de cara plana
Un diedro puede considerarse un prisma degenerado cuyas dos bases poligonales (planares) de n lados están conectadas "espalda con espalda", de modo que el objeto resultante no tiene profundidad. Los polígonos deben ser congruentes, pero pegados de tal manera que uno sea la imagen especular del otro. Esto se aplica sólo si la distancia entre las dos caras es cero; para una distancia mayor que cero, las caras son polígonos infinitos (un poco como las caras digonas del hosoedro apeirogonal, que tienen un ancho mayor que cero, son franjas infinitas).
Los diedros pueden surgir del teorema de unicidad de Alexandrov, que caracteriza las distancias en la superficie de cualquier poliedro convexo como localmente euclidianas excepto en un número finito de puntos con defecto angular positivo que suman 4π. Esta caracterización también se aplica a las distancias en la superficie de un diedro, por lo que el enunciado del teorema de Alexandrov requiere que los diedros se consideren poliedros convexos.
Algunos diedros pueden surgir como miembros del límite inferior de otras familias de poliedros: un prisma con bases digonas sería un diedro cuadrado, y una pirámide con base digona sería un diedro triangular.
Un diedro regular, con símbolo de Schläfli {n,2}, está formado por dos polígonos regulares, cada uno con símbolo de Schläfli {n}.
Como una inclinación de la esfera
Un diedro esférico está formado por dos polígonos esféricos que comparten el mismo conjunto de n vértices, en un ecuador de círculo máximo; cada polígono de un diedro esférico llena un hemisferio.
Un diedro esférico regular está formado por dos polígonos esféricos regulares que comparten el mismo conjunto de n vértices, igualmente espaciados sobre un ecuador de círculo máximo.
El poliedro regular {2,2} es autodual y es a la vez hosoedro y diedro.
| Espacio | Spherical | Euclidean | |||||
|---|---|---|---|---|---|---|---|
| Tiling Nombre | Monogonal dihedron | Digonal dihedron | Trigonal dihedron | Square dihedron | Dihedron pentagonal | ... | Apeirogonal dihedron |
| Tiling imagen |  |  |  |  |  | ... |  |
| Símbolo Schläfli | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | ... | - ¿Qué? |
| Coxeter diagrama |     | |  |  |  | ... |  |
| Caras | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | ... | 2 {Libros} |
| Edges y vertices | 1 | 2 | 3 | 4 | 5 | ... | JUEGO |
| Config de Vertex. | 1.1 | 2.2 | 3.3 | 4.4 | 5,5 | ... | JUEGO. |
Apeirogonal dihedron
As n tiende a infinito, un n-el dihedro se convierte en un dihedro apeirogonal como tessellación de 2 dimensiones:
Ditopes
Un dítopo regular es un análogo n-dimensional de un diedro, con símbolo de Schläfli {p,...,q,r,2}. Tiene dos facetas, {p,...,q,r}, que comparten todas las crestas, {p,...,q} en común.
Véase también
- Dihedral group
- Polyhedron
- Politopo
Referencias
- ^ Gausmann, Evelise; Roland Lehoucq; Jean-Pierre Luminet; Jean-Philippe Uzan; Jeffrey Weeks (2001). "Formación Topológica en Espacios Esféricos". Gravidad clásica y cuántica. 18 (23): 5155–5186. arXiv:gr-qc/0106033. Bibcode:2001CQGra..18.5155G. doi:10.1088/0264-9381/18/23/311. S2CID 34259877.
- ^ Kántor, S. (2003), "Sobre el volumen de polihedra sin límites en el espacio hiperbólico" (PDF), Beiträge zur Algebra und Geometrie, 44 (1): 145–154, MR 1990989, archivado desde el original (PDF) on 2017-02-15, recuperado 2017-02-14.
- ^ a b O'Rourke, Joseph (2010), Parejas planas con cremallera para sólidos platónicos, arXiv:1010.2450, Bibcode:2010arXiv1010.2450O
- ^ O'Rourke, Joseph (2010), En polihedra plana derivando del teorema de Alexandrov, arXiv:1007.2016, Bibcode:2010arXiv1007.2016O
- ^ Coxeter, H. S. M. (enero de 1973), Regular Polytopes (3rd ed.), Dover Publications Inc., p. 12, ISBN 0-486-61480-8
- ^ McMullen, Peter; Schulte, Egon (diciembre de 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, p. 158, ISBN 0-521-81496-0
Enlaces externos
- Weisstein, Eric W. "Dihedron". MathWorld.