Dicroísmo circular

El dicroísmo circular (CD) es el dicroísmo que involucra luz polarizada circularmente, es decir, la absorción diferencial de la luz hacia la izquierda y hacia la derecha. La luz polarizada circular izquierda (LHC) y circular derecha (RHC) representan dos posibles estados de momento angular de espín para un fotón, por lo que el dicroísmo circular también se conoce como dicroísmo por momento angular de espín. Este fenómeno fue descubierto por Jean-Baptiste Biot, Augustin Fresnel y Aimé Cotton en la primera mitad del siglo XIX. El dicroísmo circular y la birrefringencia circular son manifestaciones de la actividad óptica. Se exhibe en las bandas de absorción de moléculas quirales ópticamente activas. La espectroscopia de CD tiene una amplia gama de aplicaciones en muchos campos diferentes. En particular, UV CD se utiliza para investigar la estructura secundaria de las proteínas. UV/Vis CD se utiliza para investigar las transiciones de transferencia de carga. El CD de infrarrojo cercano se utiliza para investigar la estructura geométrica y electrónica mediante el sondeo de las transiciones d→d de metal. El dicroísmo circular vibratorio, que usa luz de la región de energía infrarroja, se usa para estudios estructurales de pequeñas moléculas orgánicas y, más recientemente, proteínas y ADN.

Principios físicos

Polarización circular de la luz

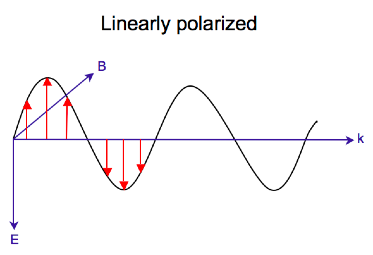
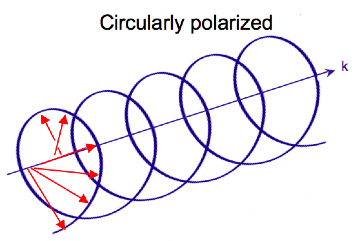
Radiación electromagnética consiste en un eléctrico E{displaystyle {fncipulo}} y magnética B{displaystyle {boldsymbol {B}} campo que oscila perpendicular entre sí y a la dirección propagante, una onda transversal. Mientras la luz polarizada linealmente ocurre cuando el vector de campo eléctrico oscila sólo en un plano, la luz polarizada circular ocurre cuando la dirección del vector de campo eléctrico gira sobre su dirección de propagación mientras que el vector conserva una magnitud constante. En un solo punto en el espacio, el piloto polarizado circularmente rastreará un círculo en un período de la frecuencia de onda, por lo tanto el nombre. Los dos diagramas a continuación muestran los vectores de campo eléctrico de luz polarizada lineal y circular, en un momento de tiempo, para una gama de posiciones; la trama del vector eléctrico polarizado circular forma un helix a lo largo de la dirección de propagación k{displaystyle {boldsymbol {k}}. Para la luz circular polarizada izquierda (LCP) con propagación hacia el observador, el vector eléctrico gira en sentido contrario. Para la luz circular polarizada derecha (RCP), el vector eléctrico gira en sentido de reloj.

Interacción de la luz polarizada circularmente con la materia

Cuando la luz polarizada circular pasa a través de un medio absorbente ópticamente activo, las velocidades entre las polarizaciones derecha e izquierda difieren (cLل ل cR{displaystyle c_{mathrm {L}neq c_{mathrm {R}así como su longitud de ondaλ λ Lل ل λ λ R{displaystyle lambda _{mathrm {L}neq lambda _{mathrm {R}) y la medida en que se absorben (ε ε Lل ل ε ε R{displaystyle varepsilon _{mathrm {L}neq varepsilon _{mathrm {R}). Diquismo circular es la diferencia Δ Δ ε ε ↑ ↑ ε ε L− − ε ε R{displaystyle Delta varepsilon equiv varepsilon _{mathrm {L}-varepsilon _{mathrm {R}. El campo eléctrico de un rayo de luz causa un desplazamiento lineal de carga al interactuar con una molécula (dipolo electrónico), mientras que su campo magnético causa una circulación de carga (dipolo magnético). Estos dos movimientos combinados causan una excitación de un electrón en un movimiento helicoidal, que incluye traducción y rotación y sus operadores asociados. La relación experimentalmente determinada entre la fuerza rotatoria R{displaystyle R. de una muestra y la Δ Δ ε ε {displaystyle Delta varepsilon } es dado por

Rexp=3hc103In⁡ ⁡ ()10)32π π 3NA∫ ∫ Δ Δ ε ε .. d.. {displaystyle R_{mathrm}={frac {3hc10^{3}ln(10)}{32pi ^{3}N_{mathrm {A}}int {fnMicroc} {Delta varepsilon } {}mathrm {d} {nu}

La fuerza de rotación también se ha determinado teóricamente,

Rtheo=12mcIm∫ ∫ Ψ Ψ gM^ ^ ()elec.dipole)Ψ Ψ edτ τ ∙ ∙ ∫ ∫ Ψ Ψ gM^ ^ ()mag.dipole)Ψ Ψ edτ τ {displaystyle ¿Qué? mathrm {Im} int Psi _{g}{widehat {M}_{mathrm {(elec.dipole)} }Psi _{e}mathrm {d} tau bullet int Psi _{g}{widehat {M}}_{mathrm {(mag.dipole)} }Psi _{e}mathrm {d} tau }

Vemos de estas dos ecuaciones que para tener no cero Δ Δ ε ε {displaystyle Delta varepsilon }, los operadores de momento dipolo eléctrico y magnético (M^ ^ ()elec.dipole){displaystyle {widehat {}_{mathrm {(elec.dipole)}}} y M^ ^ ()mag.dipole){displaystyle {widehat {}_{mathrm {(mag.dipole)}}}) debe transformarse como la misma representación irreducible. Cn{displaystyle mathrm {C} _{n} y Dn{displaystyle mathrm {} _{n} son los únicos grupos de puntos donde esto puede ocurrir, haciendo solamente moléculas chiral CD activas.

En pocas palabras, dado que la propia luz polarizada circularmente es "quiral", interactúa de manera diferente con las moléculas quirales. Es decir, los dos tipos de luz polarizada circularmente se absorben en grados diferentes. En un experimento de CD, se irradian alternativamente hacia una muestra (quiral) cantidades iguales de luz polarizada circularmente izquierda y derecha de una longitud de onda seleccionada. Una de las dos polarizaciones se absorbe más que la otra, y se mide esta diferencia de absorción dependiente de la longitud de onda, lo que produce el espectro CD de la muestra. Debido a la interacción con la molécula, el vector de campo eléctrico de la luz traza una trayectoria elíptica después de atravesar la muestra.

Es importante que la quiralidad de la molécula pueda ser conformacional en lugar de estructural. Es decir, por ejemplo, una molécula de proteína con una estructura secundaria helicoidal puede tener un CD que cambia con los cambios en la conformación.

Absorción delta

Por definición,

Δ Δ A=AL− − AR{displaystyle Delta A=A_{mathrm {L}-A_{mathrm {R},}

Donde Δ Δ A{displaystyle Delta A} (Delta Absorbancia) es la diferencia entre la absorción de la luz polarizada circular izquierda (LCP) y la derecha polarizada circularmente (RCP) (esto es lo que se suele medir). Δ Δ A{displaystyle Delta A} es una función de longitud de onda, por lo que para que una medición sea significativa la longitud de onda en la que se realizó debe ser conocido.

Dicroísmo circular molar

También se puede expresar, aplicando la ley de Beer, como:

Δ Δ A=()ε ε L− − ε ε R)Cl{displaystyle Delta A=(varepsilon _{mathrm {L}-varepsilon _{mathrm {R})Cl,}

dónde

ε ε L{displaystyle varepsilon _{mathrm {L}} y ε ε R{displaystyle varepsilon _{mathrm {R} son los coeficientes de extinción molar para la luz LCP y RCP,

C{displaystyle C} es la concentración molar,

l{displaystyle l} es la longitud del camino en centímetros (cm).

Entonces

Δ Δ ε ε =ε ε L− − ε ε R{displaystyle Delta varepsilon = varepsilon _{mathrm {L}-varepsilon ¿Qué?

es el dicroismo circular molar. Esta propiedad intrínseca es lo que generalmente se entiende por el dicroismo circular de la sustancia. Desde Δ Δ ε ε {displaystyle Delta varepsilon } es una función de longitud de onda, un valor circular del dicroismo molar (Δ Δ ε ε {displaystyle Delta varepsilon }) debe especificar la longitud de onda en la que es válida.

Efectos extrínsecos sobre el dicroísmo circular

En muchas aplicaciones prácticas del dicroísmo circular (CD), como se explica a continuación, la CD medida no es simplemente una propiedad intrínseca de la molécula, sino que depende de la conformación molecular. En tal caso, la CD también puede ser una función de la temperatura, la concentración y el entorno químico, incluidos los disolventes. En este caso, el valor de CD informado también debe especificar estos otros factores relevantes para que sea significativo.

En estructuras ordenadas que carecen de doble simetría rotacional, la actividad óptica, incluida la transmisión diferencial (y la reflexión) de ondas polarizadas circularmente, también depende de la dirección de propagación a través del material. En este caso, la llamada quiralidad 3d extrínseca está asociada con la orientación mutua del haz de luz y la estructura.

Elipticidad molar

Aunque Δ Δ A{displaystyle Delta A} se mide generalmente, por razones históricas la mayoría de las mediciones se reportan en grados de elicidad. La ellipticidad molar es el dicroismo circular corregido para la concentración. Dicroismo circular y elicidad molar, [Silencio Silencio ]{displaystyle [theta]}, son fácilmente interconvertidos por la ecuación:

La luz polarizada elíptica (violeta) se compone de contribuciones desiguales de la luz polarizada derecha (azul) y izquierda (rojo).

[Silencio Silencio ]=3298.2Δ Δ ε ε .{displaystyle [theta ]=3298.2,Delta varepsilon.

Esta relación se obtiene definiendo la elipticidad de la polarización como:

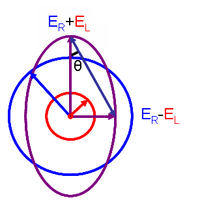
#⁡ ⁡ Silencio Silencio =ER− − ELER+EL{displaystyle tan theta ={frac {fnMicrom} {R}-E_{mathrm {L}}{E_{mathrm {R}+E_{mathrm {L}}},}

dónde

ER{displaystyle E_{mathrm {R} y EL{displaystyle E_{mathrm {L}} son las magnitudes de los vectores de campo eléctrico de la luz polarizada circular e izquierda, respectivamente.

Cuando ER{displaystyle E_{mathrm {R} iguales EL{displaystyle E_{mathrm {L}} (cuando no hay diferencia en la absorción de la luz polarizada derecha e izquierda), Silencio Silencio {displaystyle theta } es 0° y la luz se polariza linealmente. Cuando sea ER{displaystyle E_{mathrm {R} o EL{displaystyle E_{mathrm {L}} es igual a cero (cuando hay total absorción de la luz polarizada circular en una dirección), Silencio Silencio {displaystyle theta } es 45° y la luz se polariza circularmente.

Generalmente, el efecto dicroísmo circular es pequeño, por lo que #⁡ ⁡ Silencio Silencio {displaystyle tan theta } es pequeño y puede ser aproximado Silencio Silencio {displaystyle theta } en radios. Desde la intensidad o irradiación, I{displaystyle Yo..., de luz es proporcional a la plaza del vector de campo eléctrico, la elipticidad se convierte en:

Silencio Silencio ()radiantes)=()IR1/2− − IL1/2)()IR1/2+IL1/2){displaystyle theta ({text{radians}}})={frac {(I_{mathrm {R} }{1/2}-I_{mathrm {fnK} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {fnK}}} {fnK}} {f}}} {fnK}} {fnK}} {f}}}}} {f}}}} {fnKf}}}}} {f}}}}}} {f}}}}}}}}}}}}} {f}}}}}}}}}}}}} {f}} {\\f} {f} {f}}}} {f}}}} {f}} {f}}}}}} {f} {f}}}} {f}}} {f}}}} {f} {f} {f}} {f}}}}}}}}}}}}}}}}}} {f}}}}}} {f}}}}}}} {R} }{1/2}+I_{mathrm ♪♪

Entonces, al sustituir I usando la ley de Beer en forma de logaritmo natural:

I=I0e− − AIn⁡ ⁡ 10{displaystyle Yo...

La elipticidad ahora se puede escribir como:

Silencio Silencio ()radiantes)=()e− − AR2In⁡ ⁡ 10− − e− − AL2In⁡ ⁡ 10)()e− − AR2In⁡ ⁡ 10+e− − AL2In⁡ ⁡ 10)=eΔ Δ AIn⁡ ⁡ 102− − 1eΔ Δ AIn⁡ ⁡ 102+1{displaystyle theta ({text{radians}})={frac {mathrm {e} ^{frac} {-A_{mathrm {}} {fn}n 10}-mathrm {e} {fnMicroc} {fn9} {fn9} {fn0}} {fn9}} {fn9}} {fn9}} {fn9}}} {fn9}} {fn9}} {fn9}}} {fn9}} {fn9}}} {fn9}}}}}} {f}} {f}}}}}}}}}}}}}} {n9}}}}} {n9}}}}}}}}} {m}}}}}} {n9}}}} {m}}}}}}}}}}} {\\n_\\n9}}}}}}}}}} {m}}}}} {n 10}}}}}}}}}}}}}}}}} {n 10}}}}}}}}}} {m}}}}}}}}}}}}} { {-A_{mathrm {R}} {2}fn} 10}+mathrm {e} ^{{frac {cHFF} {cH00}}}cH00} ¿Qué? 10}{2}}-1}{mathrm {e} } {Delta A{frac {ln} {fn} {fn} {fn} {fn}}}}} {fn}}} {fn}}} {fn}}}}}}}} {m}} {m} {m}}}}} {m}}}}} {m}}}}} {m} {m}}} {m}} {m} {m} {m} {m}} {m} {m} {m}}}}}}}}}}}}}}}}}}}} {m} {m} {m} {m} {m} {m} {m} {m}}} {m} {s}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 10} {2}}}+1},}

Desde Δ Δ A≪ ≪ 1{displaystyle Delta All 1}, esta expresión se puede aproximar ampliando los exponenciales de una serie Taylor a las primeras órdenes y luego descartando términos de Δ Δ A{displaystyle Delta A} en comparación con la unidad y la conversión de radios a grados:

Silencio Silencio ()grados)=Δ Δ A()In⁡ ⁡ 104)()180π π ){displaystyle theta ({text{degrees}})=Delta Aleft({frac {ln} 10}{4}right)left({frac {180}{pi}right),}

La dependencia lineal de la concentración de soluto y la longitud del camino se elimina definiendo la elipticidad molar como,

[Silencio Silencio ]=100Silencio Silencio Cl{displaystyle [theta]={frac {100theta] } {Cl},}

Luego, combinando las dos últimas expresiones con la ley de Beer, la elipticidad molar se convierte en:

[Silencio Silencio ]=100Δ Δ ε ε ()In⁡ ⁡ 104)()180π π )=3298.2Δ Δ ε ε {displaystyle [theta ]=100,Delta varepsilon left({frac {ln 10}{4}right)left({frac {180}{pi }right)=3298.2,Delta varepsilon ,}

Las unidades de elipticidad molar son históricamente (grados·cm²/dmol). Para calcular la elipticidad molar, se debe conocer la concentración de la muestra (g/L), la longitud del camino celular (cm) y el peso molecular (g/mol).

Si la muestra es una proteína, el peso medio del residuo (peso molecular promedio de los residuos de aminoácidos que contiene) se usa a menudo en lugar del peso molecular, esencialmente tratando la proteína como una solución de aminoácidos. El uso de la elipticidad media de los residuos facilita la comparación de la CD de proteínas de diferente peso molecular; el uso de esta CD normalizada es importante en estudios de estructura de proteínas.

Elipticidad media del residuo

Los métodos para estimar la estructura secundaria en polímeros, proteínas y polipéptidos en particular, a menudo requieren que el espectro de elipticidad molar medido se convierta a un valor normalizado, específicamente un valor independiente de la longitud del polímero. Para este propósito se utiliza la elipticidad media de los residuos; es simplemente la elipticidad molar medida de la molécula dividida por el número de unidades monoméricas (residuos) en la molécula.

Aplicación a moléculas biológicas

Panel superior: Espectroscopia circular de dicroismo en la región de longitud de onda ultravioleta (UV-CD) de MBP-cytochrome b₆ proteína de fusión en diferentes soluciones detergentes. Muestra que la proteína en DM, así como en la solución Triton X-100, recuperó su estructura. Sin embargo, el espectro obtenido de la solución SDS muestra una disminución de la elipticidad en el rango entre 200 y 210 nm, lo que indica la recuperación de la estructura secundaria incompleta.
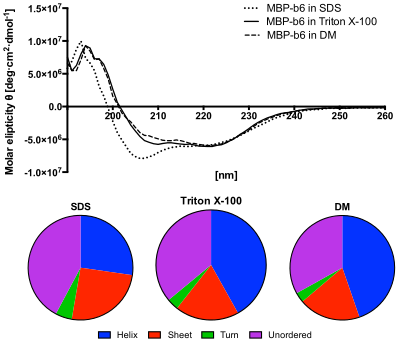
Panel inferior: El contenido de las estructuras secundarias predijo del espectro CD utilizando el algoritmo CDSSTR. La proteína en la solución SDS muestra mayor contenido de estructuras no ordenadas y menor contenido de cálices.

En general, este fenómeno se exhibirá en las bandas de absorción de cualquier molécula ópticamente activa. Como consecuencia, el dicroísmo circular es exhibido por moléculas biológicas, debido a sus componentes dextrorrotatorios y levorrotatorios. Aún más importante es que una estructura secundaria también impartirá una CD distinta a sus moléculas respectivas. Por lo tanto, la hélice alfa de las proteínas y la doble hélice de los ácidos nucleicos tienen firmas espectrales de CD representativas de sus estructuras. La capacidad de CD para dar una firma estructural representativa lo convierte en una herramienta poderosa en la bioquímica moderna con aplicaciones que se pueden encontrar en prácticamente todos los campos de estudio.

La CD está estrechamente relacionada con la técnica de dispersión rotatoria óptica (ORD) y, en general, se considera que es más avanzada. CD se mide en o cerca de las bandas de absorción de la molécula de interés, mientras que ORD se puede medir lejos de estas bandas. La ventaja de CD es evidente en el análisis de datos. Los elementos estructurales se distinguen más claramente ya que sus bandas registradas no se superponen mucho en longitudes de onda particulares como ocurre en ORD. En principio, estas dos medidas espectrales pueden interconvertirse mediante una transformada integral (relación de Kramers-Kronig), si todas las absorciones están incluidas en las medidas.

El espectro CD de las proteínas UV lejano (ultravioleta) puede revelar características importantes de su estructura secundaria. Los espectros de CD se pueden usar fácilmente para estimar la fracción de una molécula que está en la conformación de hélice alfa, la conformación de hoja beta, la conformación de giro beta o alguna otra conformación (por ejemplo, espiral aleatoria). Estas asignaciones fraccionarias imponen restricciones importantes sobre las posibles conformaciones secundarias en las que puede estar la proteína. CD no puede, en general, decir dónde se encuentran las hélices alfa que se detectan dentro de la molécula o incluso predecir por completo cuántas hay. A pesar de esto, el CD es una herramienta valiosa, especialmente para mostrar cambios en la conformación. Puede utilizarse, por ejemplo, para estudiar cómo cambia la estructura secundaria de una molécula en función de la temperatura o de la concentración de agentes desnaturalizantes, p. Cloruro de guanidinio o urea. De esta forma, puede revelar información termodinámica importante sobre la molécula (como la entalpía y la energía de desnaturalización libre de Gibbs) que de otro modo no se puede obtener fácilmente. Cualquiera que intente estudiar una proteína encontrará que la CD es una herramienta valiosa para verificar que la proteína está en su conformación nativa antes de realizar experimentos extensos y/o costosos con ella. Además, hay una serie de otros usos para la espectroscopia de CD en la química de proteínas que no están relacionados con la estimación de la fracción de hélice alfa. Además, la espectroscopia de CD se ha utilizado en estudios de interfaz bioinorgánica. Específicamente, se ha utilizado para analizar las diferencias en la estructura secundaria de una proteína modificada antes y después de la titulación con un reactivo.

El espectro CD de UV cercano (>250 nm) de las proteínas proporciona información sobre la estructura terciaria. Las señales obtenidas en la región de 250 a 300 nm se deben a la absorción, la orientación del dipolo y la naturaleza del entorno circundante de los aminoácidos fenilalanina, tirosina, cisteína (o puentes disulfuro S-S) y triptófano. A diferencia del CD de UV lejano, el espectro de CD de UV cercano no se puede asignar a ninguna estructura 3D en particular. Más bien, los espectros de CD de UV cercano brindan información estructural sobre la naturaleza de los grupos prostéticos en las proteínas, por ejemplo, los grupos hemo en la hemoglobina y el citocromo c.

La espectroscopia de CD visible es una técnica muy poderosa para estudiar las interacciones metal-proteína y puede resolver las transiciones electrónicas d-d individuales como bandas separadas. Los espectros de CD en la región de luz visible solo se producen cuando un ion metálico se encuentra en un entorno quiral, por lo que no se detectan iones metálicos libres en solución. Esto tiene la ventaja de que solo se observa el metal unido a la proteína, por lo que la dependencia del pH y las estequiometrías se obtienen fácilmente. La actividad óptica en los complejos de iones de metales de transición se ha atribuido a efectos configuracionales, conformacionales y vecinales. Klewpatinond y Viles (2007) han producido un conjunto de reglas empíricas para predecir la aparición de espectros de CD visibles para complejos planos cuadrados de Cu²⁺ y Ni²⁺ que involucran histidina y coordinación de la cadena principal.

La CD brinda información estructural menos específica que la cristalografía de rayos X y la espectroscopia de RMN de proteínas, por ejemplo, que brindan datos de resolución atómica. Sin embargo, la espectroscopia de CD es un método rápido que no requiere grandes cantidades de proteínas ni un procesamiento extenso de datos. Por lo tanto, la CD se puede utilizar para estudiar una gran cantidad de condiciones de disolventes, temperatura variable, pH, salinidad y la presencia de varios cofactores.

La espectroscopia de CD se usa generalmente para estudiar proteínas en solución y, por lo tanto, complementa los métodos que estudian el estado sólido. Esto también es una limitación, ya que muchas proteínas están incrustadas en las membranas en su estado nativo, y las soluciones que contienen estructuras de membrana a menudo se dispersan fuertemente. El CD a veces se mide en películas delgadas.

La espectroscopia CD también se ha realizado utilizando materiales semiconductores como TiO₂ para obtener grandes señales en el rango UV de longitudes de onda, donde a menudo ocurren las transiciones electrónicas de las biomoléculas.

Limitaciones experimentales

La CD también se ha estudiado en carbohidratos, pero con un éxito limitado debido a las dificultades experimentales asociadas con la medición de espectros de CD en la región ultravioleta de vacío (VUV) del espectro (100-200 nm), donde las bandas de CD correspondientes los carbohidratos no sustituidos mienten. Los carbohidratos sustituidos con bandas por encima de la región VUV se han medido con éxito.

La medición de CD también se complica por el hecho de que los sistemas tampón acuosos típicos a menudo absorben en el rango en el que las características estructurales exhiben una absorción diferencial de la luz polarizada circularmente. Los tampones de fosfato, sulfato, carbonato y acetato generalmente son incompatibles con CD a menos que se diluyan extremadamente, p. en el rango de 10 a 50 mM. El sistema de búfer TRIS debe evitarse por completo cuando se realiza un CD de ultravioleta lejano. Los compuestos de borato y onio se utilizan a menudo para establecer el rango de pH adecuado para los experimentos de CD. Algunos experimentadores han sustituido el ion cloruro por fluoruro porque el fluoruro absorbe menos en el UV lejano, y algunos han trabajado en agua pura. Otra técnica, casi universal, es minimizar la absorción de solventes mediante el uso de celdas de paso óptico más cortas cuando se trabaja en el UV lejano; las longitudes de paso óptico de 0,1 mm no son infrecuentes en este trabajo.

Además de medirse en sistemas acuosos, la CD, en particular la CD UV lejana, se puede medir en solventes orgánicos, p. etanol, metanol, trifluoroetanol (TFE). Este último tiene la ventaja de inducir la formación de estructuras de proteínas, induciendo láminas beta en algunas y hélices alfa en otras, que no mostrarían en condiciones acuosas normales. Sin embargo, los disolventes orgánicos más comunes, como el acetonitrilo, el THF, el cloroformo y el diclorometano, son incompatibles con el CD de ultravioleta lejano.

Puede ser de interés señalar que los espectros de CD de proteínas utilizados en la estimación de la estructura secundaria están relacionados con las absorciones orbitales π a π* de los enlaces amida que unen los aminoácidos. Estas bandas de absorción se encuentran en parte en el llamado ultravioleta de vacío (longitudes de onda inferiores a unos 200 nm). La región de longitud de onda de interés es realmente inaccesible en el aire debido a la fuerte absorción de luz por parte del oxígeno en estas longitudes de onda. En la práctica, estos espectros no se miden en el vacío sino en un instrumento sin oxígeno (lleno de gas nitrógeno puro).

Una vez que se ha eliminado el oxígeno, quizás el segundo factor técnico más importante para trabajar por debajo de 200 nm es diseñar el resto del sistema óptico para que tenga bajas pérdidas en esta región. Crítico en este sentido es el uso de espejos aluminizados cuyos recubrimientos han sido optimizados para una baja pérdida en esta región del espectro.

La fuente de luz habitual en estos instrumentos es una lámpara de xenón de arco corto y alta presión. Las lámparas de arco de xenón ordinarias no son adecuadas para su uso en UV bajo. En su lugar, se deben utilizar lámparas especialmente construidas con envolturas hechas de sílice fundida sintética de alta pureza.

La luz de las fuentes de sincrotrón tiene un flujo mucho mayor en longitudes de onda cortas y se ha utilizado para grabar CD hasta 160 nm. En 2010, el espectrofotómetro de CD en la instalación de anillo de almacenamiento de electrones ISA en la Universidad de Aarhus en Dinamarca se utilizó para registrar espectros de CD en estado sólido hasta 120 nm. En el nivel de la mecánica cuántica, la densidad de características del dicroísmo circular y la rotación óptica son idénticas. La dispersión rotatoria óptica y el dicroísmo circular comparten el mismo contenido de información cuántica.