Diagrama de hasse

En la teoría del orden, un Diagrama de Hasse ()Alemán: [Suena]) es un tipo de diagrama matemático usado para representar un conjunto parcialmente ordenado finito, en la forma de un dibujo de su reducción transitiva. Concretamente, para un conjunto parcialmente ordenado ()S,≤ ≤ ){displaystyle (S,leq)} uno representa cada elemento S{displaystyle S. como un vértice en el plano y dibuja un segmento de línea o curva que va arriba de un vértice x{displaystyle x} a otro vértice Sí.{displaystyle y} siempre Sí.{displaystyle y} cubiertas x{displaystyle x} (es decir, cuando sea xل ل Sí.{displaystyle xneq y}, x≤ ≤ Sí.{displaystyle xleq y} y no hay z{displaystyle z} distintos x{displaystyle x} y Sí.{displaystyle y} con x≤ ≤ z≤ ≤ Sí.{displaystyle xleq zleq y}). Estas curvas pueden cruzarse entre sí pero no deben tocar ningún vértic que no sea su punto final. Tal diagrama, con vértices etiquetados, determina singularmente su orden parcial.

Los diagramas de Hasse llevan el nombre de Helmut Hasse (1898–1979); según Garrett Birkhoff, se llaman así por el uso efectivo que Hasse hizo de ellos. Sin embargo, Hasse no fue el primero en utilizar estos diagramas. Un ejemplo anterior a Hasse se puede encontrar en Henri Gustave Vogt (1895). Aunque los diagramas de Hasse se idearon originalmente como una técnica para hacer dibujos a mano de conjuntos parcialmente ordenados, más recientemente se han creado automáticamente utilizando técnicas de dibujo de gráficos.

La frase "Diagrama de Hasse" también puede referirse a la reducción transitiva como un gráfico acíclico dirigido abstracto, independientemente de cualquier dibujo de ese gráfico, pero este uso se evita aquí.

Diseño de diagramas

Aunque los diagramas de Hasse son herramientas sencillas e intuitivas para trabajar con conjuntos de poses finitos, resulta bastante difícil dibujar diagramas "buenos" diagramas La razón es que, en general, hay muchas formas posibles de dibujar un diagrama de Hasse para una pose dada. La técnica simple de comenzar simplemente con los elementos mínimos de un pedido y luego dibujar elementos mayores de forma incremental a menudo produce resultados bastante pobres: las simetrías y la estructura interna del pedido se pierden fácilmente.

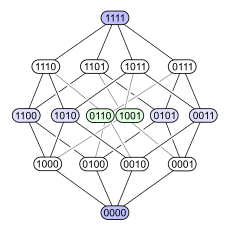
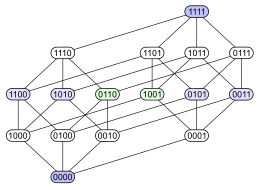
El siguiente ejemplo demuestra la cuestión. Considere el conjunto de potencia de un 4-elemento ordenado por inclusión ⊆ ⊆ {displaystyle subseteq }. A continuación se presentan cuatro diagramas diferentes de Hasse para este orden parcial. Cada subconjunto tiene un nodo etiquetado con una codificación binaria que muestra si un determinado elemento está en el subconjunto (1) o no (0):

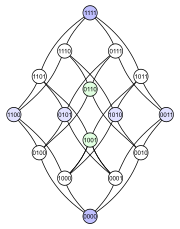El primer diagrama deja en claro que el conjunto de potencia es una pose graduada. El segundo diagrama tiene la misma estructura graduada, pero al hacer algunos bordes más largos que otros, enfatiza que el cubo de 4 dimensiones es una unión combinatoria de dos cubos de 3 dimensiones, y que un tetraedro (3-politopo abstracto) también fusiona dos triángulos (2-politopos abstractos). El tercer diagrama muestra algo de la simetría interna de la estructura. En el cuarto diagrama, los vértices están dispuestos en una cuadrícula de 4×4.

Planaridad hacia arriba

Si un orden parcial se puede dibujar como un diagrama de Hasse en el que no se cruzan dos aristas, se dice que su gráfico de cobertura es planar hacia arriba. Se conocen varios resultados sobre la planaridad hacia arriba y sobre la construcción del diagrama de Hasse sin cruces:

• Si el orden parcial a dibujar es una celosía, entonces se puede dibujar sin cruces si y sólo si tiene dimensión de orden en la mayoría de dos. En este caso, se puede encontrar un dibujo que no se cruce con coordenadas cartesianas de los elementos de sus posiciones en las dos órdenes lineales que dan cuenta de la dimensión del orden, y luego girando el dibujo en sentido contrario por un ángulo de 45 grados.
• Si el orden parcial tiene en la mayoría de un elemento mínimo, o tiene en la mayoría de un elemento maximal, entonces puede ser probado en tiempo lineal si tiene un diagrama de Hasse no cruzando.
• Es NP-completo determinar si un orden parcial con múltiples fuentes y sumideros puede ser dibujado como un diagrama de Hasse libre de cruces. Sin embargo, encontrar un diagrama de Hasse libre de cruces es traccionable de parámetros fijos cuando se parametiza con el número de puntos de articulación y componentes triconectados de la reducción transitiva del orden parcial.
• Si Sí.- se especifican coordenadas de los elementos de un orden parcial, luego se puede encontrar un diagrama de Hasse libre de cruces que respete esas asignaciones de coordenadas en tiempo lineal, si existe tal diagrama. En particular, si la pose de entrada es una postura de grado, es posible determinar en tiempo lineal si hay un diagrama de Hasse libre de cruce en el que la altura de cada vértice es proporcional a su rango.

Notación UML

En ingeniería de software, las clases de un sistema de software y la relación de herencia entre estas clases a menudo se representan mediante un diagrama de clases, una forma de diagrama de Hasse en el que los bordes que conectan las clases se dibujan como segmentos de línea continua con un triángulo abierto en el final de la superclase.