Diagrama de euler


Un diagrama de Euler (, OY-lər) es un medio esquemático para representar conjuntos y sus relaciones. Son particularmente útiles para explicar jerarquías complejas y definiciones superpuestas. Son similares a otra técnica de diagramación de conjuntos, los diagramas de Venn. A diferencia de los diagramas de Venn, que muestran todas las relaciones posibles entre diferentes conjuntos, el diagrama de Euler muestra sólo relaciones relevantes.
El primer uso de los "círculos eulerianos" Se atribuye comúnmente al matemático suizo Leonhard Euler (1707-1783). En Estados Unidos, los diagramas de Venn y Euler se incorporaron como parte de la enseñanza de la teoría de conjuntos como parte del nuevo movimiento matemático de la década de 1960. Desde entonces, también han sido adoptados por otros campos curriculares como la lectura, así como por organizaciones y empresas.
Los diagramas de Euler consisten en formas cerradas simples en un plano bidimensional y cada una representa un conjunto o categoría. Cómo o si estas formas se superponen demuestra las relaciones entre los conjuntos. Cada curva divide el plano en dos regiones o "zonas": la interior, que representa simbólicamente los elementos del conjunto, y la exterior, que representa todos los elementos que no son miembros del conjunto. Las curvas que no se superponen representan conjuntos disjuntos, que no tienen elementos en común. Dos curvas que se superponen representan conjuntos que se cruzan, que tienen elementos comunes; la zona dentro de ambas curvas representa el conjunto de elementos comunes a ambos conjuntos (la intersección de los conjuntos). Una curva completamente dentro del interior de otra es un subconjunto de ésta.
Los diagramas de Venn son una forma más restrictiva de los diagramas de Euler. Un diagrama de Venn debe contener las 2n zonas de superposición lógicamente posibles entre sus curvas n, que representen todas las combinaciones de inclusión/exclusión de sus conjuntos constituyentes. . Las regiones que no forman parte del conjunto se indican coloreándolas de negro, a diferencia de los diagramas de Euler, donde la pertenencia al conjunto se indica tanto por superposición como por color.
Historia



Como se muestra en la ilustración de la derecha, Sir William Hamilton afirmó erróneamente que el uso original de los círculos para "sensualizar... las abstracciones de la lógica" no fue Euler (1707-1783) sino Weise (1642-1708); sin embargo, este último libro fue escrito en realidad por Johann Christian Lange, y no por Weise. Hace referencia a las Cartas a una princesa alemana de Euler.
En la ilustración de Hamilton de las cuatro proposiciones categóricas que pueden ocurrir en un silogismo, como lo simbolizan los dibujos A, E, I y O son:
- A: El Universal Affirmative
- Ejemplo: "Todos los metales son elementos."
- E: El Negativo universal
- Ejemplo: "Ningún metal es sustancias compuestas".
- I: El Particulares afirmativas
- Ejemplo: "Algunos metales son frágiles".
- O: El Negativo especial
- Ejemplo: "Algunos metales no son frágiles."
Venn (1834-1923) comenta sobre la notable prevalencia del diagrama de Euler:
- "... de los primeros sesenta tratados lógicos, publicados durante el siglo pasado o así, que fueron consultados para este propósito - algo al azar, como sucedieron ser más accesibles - parecía que treinta cuatro apelaron a la ayuda de los diagramas, casi todos estos que hacen uso del esquema Eulerian."

Sin embargo, sostuvo, "la inaplicabilidad de este esquema a los efectos de una lógica realmente general" y luego notó que,
- “Se ajusta, pero mal, incluso con las cuatro proposiciones de la lógica común a la que se aplica normalmente. ”
Venn termina su capítulo con la observación ilustrada en los ejemplos siguientes: que su uso se basa en la práctica y la intuición, no en una práctica algorítmica estricta:
- “De hecho... esos diagramas no sólo no encajan con el esquema ordinario de proposiciones que se emplean para ilustrar, sino que no parecen tener ningún esquema reconocido de proposiciones a las que puedan estar afiliados constantemente. ”
Finalmente, en su obra Venn llega a una crítica crucial (en cursiva en la cita siguiente); observe en la ilustración de Hamilton que el O (Negativo particular) y I (Afirmativo particular) simplemente se rotan:
- “Ahora venimos a los círculos conocidos de Euler que se describen por primera vez en su Lettres a une Princesse d'Allemagne ()Cartas 102-105). El punto débil de estos consiste en el hecho de que sólo ilustran en rigor las relaciones reales de clases entre sí, en lugar del conocimiento imperfecto de estas relaciones que podemos poseer, o desea transmitir, por medio de la proposición. En consecuencia, no encajarán con las proposiciones de la lógica común, sino que exigirán la constitución de un nuevo grupo de proposiciones elementales apropiadas... Este defecto debe haber sido notado desde el primer en el caso de lo afirmativo y negativo particular, porque el mismo diagrama se emplea comúnmente para defenderlos a ambos, lo que hace indiferentemente bien”.[italics added]
Cualquiera que sea el caso, armado con estas observaciones y críticas, Venn demuestra cómo derivó lo que se conoce como sus diagramas de Venn a partir de los "... diagramas de Euler anticuados". En particular, Venn da un ejemplo, que se muestra a la izquierda.
En 1914, Couturat (1868–1914) había etiquetado los términos como se muestra en el dibujo de la derecha. Además, había etiquetado la región exterior (que se muestra como a'b'c&# 39;) también. Explica sucintamente cómo utilizar el diagrama: hay que tachar las regiones que van a desaparecer:
- "El método de Venn se traduce en diagramas geométricos que representan a todos los constituyentes, de modo que, para obtener el resultado, sólo necesitamos strike out (by shading) aquellos que son hechos para desaparecer por los datos del problema."[italics añadido]
Dadas las asignaciones de Venn, entonces, las áreas no sombreadas dentro de los círculos se pueden sumar para producir la siguiente ecuación para el ejemplo de Venn:
- "NO Sí. es z y TODOS x es Sí.por lo tanto NO x es z"tiene la ecuación x'Sí.z' + xSí.z' + x'Sí.'z para la zona descubierta dentro los círculos (pero esto no es totalmente correcto; véase el siguiente párrafo).
En Venn el fondo que rodea los círculos no aparece: es decir, el término marcado "0", x'y'z'. En ninguna parte se comenta ni se etiqueta, pero Couturat corrige esto en su dibujo. La ecuación correcta debe incluir esta área sin sombrear que se muestra en negrita:
- "NO Sí. es z y TODOS x es Sí.por lo tanto NO x es z"tiene la ecuación x'Sí.z' + xSí.z' + x'Sí.'z + x'Sí.'z'.
En el uso moderno, el diagrama de Venn incluye una "caja" que rodea todos los círculos; esto se llama universo del discurso o dominio del discurso.
Couturat observó que, de manera algorítmica directa (formal, sistemática), no se pueden derivar ecuaciones booleanas reducidas, ni muestra cómo llegar a la conclusión "NO x es z". Couturat concluyó que el proceso "tiene... serios inconvenientes como método para resolver problemas lógicos":
- "No muestra cómo se exponen los datos mediante la cancelación de ciertos componentes, ni muestra cómo combinar los componentes restantes para obtener las consecuencias buscadas. En resumen, sirve sólo para exhibir un solo paso en el argumento, a saber, la ecuación del problema; no dispensa ni con los pasos anteriores, es decir, "el crecimiento del problema en una ecuación" y la transformación del local, ni con los pasos posteriores, es decir, las combinaciones que conducen a las diversas consecuencias. Por lo tanto es de muy poco uso, ya que los constituyentes pueden ser representados por símbolos algebraicos tanto como por regiones planas, y son mucho más fáciles de tratar en esta forma."
Así, la cuestión quedaría hasta 1952, cuando Maurice Karnaugh (1924-2022) adaptaría y ampliaría un método propuesto por Edward W. Veitch; este trabajo se basaría en el método de la tabla de verdad definido con precisión por Emil Post y la aplicación de la lógica proposicional a la lógica de conmutación por (entre otros) Shannon, Stibitz y Turing. Por ejemplo, Hill & Peterson (1968) presenta el diagrama de Venn con sombreado y todo. Dan ejemplos de diagramas de Venn para resolver problemas de circuitos de conmutación, pero terminan con esta afirmación:
- "Para más de tres variables, la forma ilustrativa básica del diagrama Venn es inadecuada. Las extensiones son posibles, sin embargo, la más conveniente de las cuales es el mapa de Karnaugh, que se discutirá en el capítulo 6."
En el Capítulo 6, sección 6.4 "Representación del mapa de Karnaugh de funciones booleanas" comienzan con:
- "El mapa de Karnaugh1 [1Karnaugh 1953] es una de las herramientas más poderosas en el repertorio del diseñador lógico.... Un mapa de Karnaugh puede ser considerado como una forma pictórica de una tabla de verdad o como una extensión del diagrama Venn."
La historia del desarrollo de Karnaugh de su "gráfico" o "mapa" El método es oscuro. La cadena de citas se convierte en un juego académico de "crédito, crédito; ¿Quién se lleva el crédito?": Karnaugh (1953) hizo referencia a Veitch (1952), Veitch, hizo referencia a Shannon (1938), y Shannon (1938), a su vez hizo referencia (entre otros autores de textos de lógica) Costura (1914). En el método de Veitch las variables se ordenan en un rectángulo o cuadrado; Como se describe en el mapa de Karnaugh, Karnaugh en su método cambió el orden de las variables para corresponder a lo que se conoce como (los vértices de) un hipercubo.
Relación entre los diagramas de Euler y Venn

Los diagramas de Venn son una forma más restrictiva de los diagramas de Euler. Un diagrama de Venn debe contener las 2n zonas de superposición lógicamente posibles entre sus curvas n, que representen todas las combinaciones de inclusión/exclusión de sus conjuntos constituyentes. . Las regiones que no forman parte del conjunto se indican coloreándolas de negro, a diferencia de los diagramas de Euler, donde la pertenencia al conjunto se indica tanto por superposición como por color. Cuando el número de conjuntos supera los 3, un diagrama de Venn se vuelve visualmente complejo, especialmente en comparación con el diagrama de Euler correspondiente. La diferencia entre los diagramas de Euler y Venn se puede ver en el siguiente ejemplo. Tome los tres conjuntos:
Los diagramas de Euler y Venn de esos conjuntos son:
- Diagrama de Euler
- diagrama de veneno
En un entorno lógico, se puede utilizar la semántica de la teoría de modelos para interpretar diagramas de Euler, dentro de un universo de discurso. En los ejemplos siguientes, el diagrama de Euler muestra que los conjuntos Animal y Mineral son disjuntos ya que las curvas correspondientes son disjuntas, y también que el conjunto Cuatro Patas i> es un subconjunto del conjunto de Animals. El diagrama de Venn, que utiliza las mismas categorías de Animal, Mineral y Cuatro Patas, no resume estas relaciones. Tradicionalmente, el vacío de un conjunto en los diagramas de Venn se representa mediante sombreado en la región. Los diagramas de Euler representan el vacío ya sea por sombreado o por la ausencia de una región.
A menudo se impone un conjunto de condiciones de buena formación; Estas son restricciones topológicas o geométricas impuestas a la estructura del diagrama. Por ejemplo, se podría imponer la conexión de zonas, o se podría prohibir la concurrencia de curvas o puntos múltiples, al igual que la intersección tangencial de curvas. En el diagrama adyacente, ejemplos de pequeños diagramas de Venn se transforman en diagramas de Euler mediante secuencias de transformaciones; algunos de los diagramas intermedios tienen concurrencia de curvas. Sin embargo, este tipo de transformación de un diagrama de Venn con sombreado en un diagrama de Euler sin sombreado no siempre es posible. Hay ejemplos de diagramas de Euler con 9 conjuntos que no se pueden dibujar usando curvas cerradas simples sin la creación de zonas no deseadas, ya que tendrían que tener gráficos duales no planos.
Ejemplo: diagrama de Euler a Venn y mapa de Karnaugh
Este ejemplo muestra los diagramas de Euler y Venn y el mapa de Karnaugh derivando y verificando la deducción "Ningún X es Z s". En la ilustración y la tabla se utilizan los siguientes símbolos lógicos:
- 1 se puede leer como "verdad", 0 como "falso"
- ~ for NOT and abbreviated to ' when illustrating the minterms e.g. x' =definida NO x,
- + para Booleano OR (de álgebra booleana: 0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 1 = 1)
- " (lógica Y) entre las proposiciones; en los minutos Y se omite de una manera similar a la multiplicación aritmética: por ejemplo x'y'z =definida ~x & ~y & z (De álgebra booleana: 0·0 = 0, 0·1 = 1·0 = 0, 1·1 = 1, donde "·" se muestra para la claridad)
- → (IMPLICACIÓN Alógica): leer como IF... A continuación, o " IMPLIES ", P → Q = definida NO P O Q

Dada una conclusión propuesta como "Ningún X es un Z", se puede comprobar si es o no una deducción correcta mediante el uso. de una tabla de verdad. El método más sencillo es poner la fórmula inicial a la izquierda (abreviarla como P) y poner la (posible) deducción a la derecha (abreviarla como Q) y conectar los dos con implicación lógica, es decir, P → Q, leídos como SI P ENTONCES Q. Si la evaluación de la tabla de verdad produce todos unos bajo el signo de implicación (→, el llamado conectivo mayor), entonces P → Q es una tautología. Ante este hecho, uno puede "desprenderse" la fórmula de la derecha (abreviada como Q) de la manera descrita debajo de la tabla de verdad.
Dado el ejemplo anterior, la fórmula para los diagramas de Euler y Venn es:
- "No Ys Zs" y "All Xs Ys": (~(y) z) " (x → y) =definida P
Y la deducción propuesta es:
- "No Xs Zs": (~ (x < z) =definida Q
Así que ahora la fórmula a evaluar se puede abreviar a:
- (~(y " z) " (x → y) → (~ (x " z) P → Q
- IF ("No Ys Zs" y "All Xs Ys) THEN ("No Xs Zs)
| Plaza no. | Venn, región de Karnaugh | x | Sí. | z | # | (y | " | z) | " | (x | → | y)) | → | # | (x | " | z) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | x'y'z ' | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | ||
| 1 | x'y'z | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | ||
| 2 | x'yz ' | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | ||
| 3 | x'yz | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | ||
| 4 | xy'z ' | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | ||
| 5 | xy'z | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | ||
| 6 | xyz ' | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| 7 | xyz | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
En este punto, la implicación anterior P → Q (es decir, ~(y & z) & (x → y)) → ~(x & z )) sigue siendo una fórmula, y la deducción – el "desapego" de Q de P → Q – no ha ocurrido. Pero dada la demostración de que P → Q es tautología, ahora está preparado el escenario para el uso del procedimiento del modus ponens para "separar" P: "Ninguna X es Zs" y prescindir de los términos de la izquierda.
Modus ponens (o "la regla fundamental de inferencia") a menudo se escribe de la siguiente manera: Los dos términos de la izquierda, P → < i>Q y P, se llaman premisas (por convención unidas por una coma), el símbolo ⊢ significa "rendimiento" (en el sentido de deducción lógica), y el término de la derecha se llama conclusión:
- P → Q, P ⊢ Q
Para que el modus ponens tenga éxito, ambas premisas P → Q y P deben ser verdaderas. Porque, como se demostró anteriormente, la premisa P → Q es una tautología, la "verdad" Siempre es así sin importar cómo se valoren x, y y z, pero la "verdad" solo es el caso para P en aquellas circunstancias en las que P se evalúa como "verdadero" (por ejemplo, filas 0 O 1 O 2 O 6: x'y'z' ; + x'y'z + x'yz' + xyz' = x'y' + yz').
- P → Q P ⊢ Q
- i.e.: (~(y " z) " (x → y) → (~ (x " z) (~(y " z) " (x → y))
- IF "No Ys Zs" y "All Xs Ys Entonces "No Xs Z"No" Ys Zs" y "All Xs Y"No" Xs Zs
Ahora uno es libre de "separar" la conclusión "Ninguna X es Z", tal vez para usarla en una deducción posterior (o como tema de conversación).
El uso de implicaciones tautológicas significa que existen otras deducciones posibles además de "Ninguna X es Zs"; El criterio para una deducción exitosa es que los 1 bajo el conectivo submayor de la derecha incluyen todos los 1 bajo el conectivo submayor de la izquierda (el conectivo mayor siendo la implicación que da como resultado la tautología). Por ejemplo, en la tabla de verdad, en el lado derecho de la implicación (→, el símbolo conectivo mayor), la columna en negrita debajo del símbolo conectivo submayor " ~ " tiene los mismos 1 que aparecen en la columna en negrita debajo del conectivo subprincipal izquierdo & (filas 0, 1 , 2 y 6), más dos más (filas 3 y 4).
Galería
- Un diagrama Venn muestra todas las intersecciones posibles.
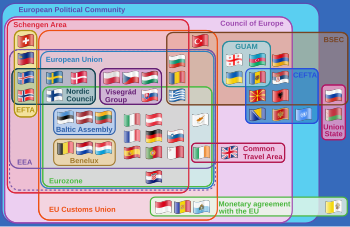
- El diagrama Euler visualiza una situación real, las relaciones entre varias organizaciones supranacionales europeas. (versión clicable)
- Diagrama Humoroso que compara los diagramas Euler y Venn.
- Diagrama de Euler de tipos de triángulos, utilizando la definición que los triángulos isosceles tienen al menos (en lugar de exactamente) 2 lados iguales.
- Esquema Euler de terminología de las Islas Británicas.
- Un diagrama Euler que categoriza diferentes tipos de metaheurística.
- Un Diagrama Euler que muestra la relación entre Homografías, homófonos y sinónimos.
- Los 22 (de 256) diagramas de Venn esencialmente diferentes con 3 círculos (top) y sus correspondientes diagramas Euler (Abajo)
Algunos de los diagramas de Euler no son típicos, y algunos son incluso equivalentes a los diagramas de Venn. Las zonas están sombreadas para indicar que no contienen elementos. - Henri Milne -Edwards's (1844) diagrama de relaciones de animales vertebrados, ilustrado como una serie de conjuntos anidados.
- Eugenio diagrama de números debajo de 100