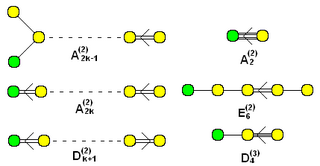
Diagrama de Dynkin

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Representación pictórica de la simetría

En el campo matemático de la teoría de Lie, un diagrama de Dynkin, llamado así por Eugene Dynkin, es un tipo de gráfico con algunos bordes duplicados o triplicados (dibujados como una línea doble o triple). Los diagramas de Dynkin surgen en la clasificación de álgebras de Lie semisimples sobre campos algebraicamente cerrados, en la clasificación de grupos de Weyl y otros grupos de reflexión finitos, y en otros contextos. Varias propiedades del diagrama de Dynkin (como si contiene múltiples aristas o sus simetrías) corresponden a características importantes del álgebra de Lie asociada.

El término "diagrama de Dynkin" puede ser ambiguo. En algunos casos, se supone que los diagramas de Dynkin son dirigidos, en cuyo caso corresponden a sistemas de raíces y álgebras de Lie semisimples, mientras que en otros casos se supone que son no dirigidos, en cuyo caso corresponden a grupos de Weyl. En este artículo, el "Diagrama de Dynkin" significa diagrama de Dynkin dirigido, y los diagramas de Dynkin no dirigidos se denominarán explícitamente así.

Clasificación de álgebras de Lie semisimples

El interés fundamental de los diagramas de Dynkin es que clasifican álgebras de Lie semisimples sobre campos algebraicamente cerrados. Uno clasifica tales álgebras de Lie a través de su sistema raíz, que puede representarse mediante un diagrama de Dynkin. Luego, se clasifican los diagramas de Dynkin de acuerdo con las restricciones que deben satisfacer, como se describe a continuación.

Omitir la dirección en los bordes del gráfico corresponde a reemplazar un sistema raíz por el grupo de reflexión finito que genera, el llamado grupo de Weyl y, por lo tanto, los diagramas de Dynkin no dirigidos clasifican los grupos de Weyl.

Tienen la siguiente correspondencia para las álgebras de Lie asociadas a grupos clásicos sobre los números complejos:

$A_{n}$ : ${mathfrak {sl}}_{{n+1}}$ , el álgebra especial de Lie linear.
$B_{n}$ : ${mathfrak {so}}_{{2n+1}}$ , la ortogonal especial extradimensional Lie algebra.
$C_{n}$ : ${mathfrak {sp}}_{{2n}}$ , el álgebra de Lie symplectic.
$D_{n}$ : ${mathfrak {so}}_{{2n}}$ , la ortogonal especial Álgebra de mentira ( $1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ ).

Para los grupos excepcionales, los nombres del álgebra de Lie y el diagrama de Dynkin asociado coinciden.

Clasificaciones relacionadas

Los diagramas de Dynkin se pueden interpretar como una clasificación de muchos objetos distintos y relacionados, y la notación "A_n, B_n,..." se utiliza para referirse a todas tales interpretaciones, según el contexto; esta ambigüedad puede ser confusa.

La clasificación central es que un álgebra de Lie simple tiene un sistema raíz, al que se asocia un diagrama de Dynkin (orientado); los tres pueden denominarse B_n, por ejemplo.

El diagrama de Dynkin noorientado es una forma de diagrama de Coxeter y corresponde al grupo de Weyl, que es el grupo de reflexión finito asociado al sistema raíz. Por lo tanto, B_n puede referirse al diagrama no orientado (un tipo especial de diagrama de Coxeter), al grupo de Weyl (un grupo de reflexión concreto) o al grupo abstracto de Coxeter.

Aunque el grupo de Weyl es abstractamente isomorfo al grupo de Coxeter, un isomorfismo específico depende de una elección ordenada de raíces simples. Del mismo modo, mientras que la notación de diagrama de Dynkin está estandarizada, la notación de diagrama y grupo de Coxeter es variada y, a veces, concuerda con la notación de diagrama de Dynkin y, a veces, no.

Por último, a veces los objetos asociados se denominan con la misma notación, aunque esto no siempre se puede hacer con regularidad. Ejemplos incluyen:

La celosía de la raíz generada por el sistema raíz, como en la celosía E8. Esto es naturalmente definido, pero no uno a uno – por ejemplo, A₂ and G₂ Ambos generan la celosía hexagonal.
Un politopo asociado – por ejemplo, el politopo Gosset 421 puede denominarse "el E₈ politopo", como sus vértices se derivan de la E₈ sistema raíz y tiene el E₈ Coxeter grupo como grupo de simetría.
Una forma cuadrática asociada o múltiple – por ejemplo, el múltiple E8 tiene forma de intersección dada por el E₈ Lattice.

Estas últimas notaciones se usan principalmente para objetos asociados con diagramas excepcionales: los objetos asociados con los diagramas normales (A, B, C, D) tienen nombres tradicionales.

El índice (el n) equivale al número de nodos en el diagrama, el número de raíces simples en una base, la dimensión de la celosía raíz y el lazo del sistema raíz, el número de generadores del grupo Coxeter, y el rango del álgebra Lie. Sin embargo, n no es igual a la dimensión del módulo de definición (una representación fundamental) del álgebra de Lie – el índice en el diagrama de Dynkin no debe confundirse con el índice en el álgebra de Lie. Por ejemplo, $B_{4}$ corresponde a ${mathfrak {so}}_{2cdot 4+1}={mathfrak {so}}_{9},$ que actúa naturalmente en el espacio 9-dimensional, pero tiene rango 4 como álgebra de Lie.

Los diagramas de Dynkin simplemente enlazados, aquellos sin múltiples aristas (A, D, E) clasifican muchos otros objetos matemáticos; ver discusión en clasificación ADE.

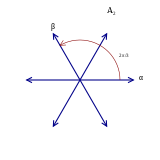
Ejemplo: A2

Por ejemplo, el símbolo $A_{2}$ puede referirse a:

El Dynkin diagram con 2 nudos conectados, , que también puede ser interpretado como Coxeter diagrama.
El root system con 2 raíces simples a $2pi /3$ (120 grados) ángulo.
El Lie algebra ${mathfrak {sl}}_{2+1}={mathfrak {sl}}_{3}$ de rango 2.
El Grupo Weyl de las simetrías de las raíces (reflexiones en la ortogonal hiperplano a las raíces), isomorfo al grupo simétrico $S_{3}$ (de orden 6).
El resumen Coxeter group, presentado por generadores y relaciones, $leftlangle r_{1},r_{2}mid (r_{1})^{2}=(r_{2})^{2}=(r_{i}r_{j})^{3}=1rightrangle.$

Construcción a partir de sistemas raíz

Considere un sistema de raíces, que se supone que se reduce e integral (o "cristallographic"). En muchas aplicaciones, este sistema raíz surgirá de un álgebra de Lie semisimple. Vamos $Delta$ ser un conjunto de raíces simples positivas. Luego construimos un diagrama de $Delta$ como sigue. Forma un gráfico con un vértice para cada elemento $Delta$ . Luego insertar bordes entre cada par de vértices según la siguiente receta. Si las raíces correspondientes a los dos vértices son ortogonales, no hay borde entre los vértices. Si el ángulo entre las dos raíces es de 120 grados, ponemos un borde entre los vértices. Si el ángulo es de 135 grados, ponemos dos bordes, y si el ángulo es de 150 grados, ponemos tres bordes. (Estos cuatro casos agotan todos los ángulos posibles entre pares de raíces simples positivas.) Finalmente, si hay bordes entre un par dado de vértices, los decoramos con una flecha apuntando desde el vértice correspondiente a la raíz más larga al vértice correspondiente al más corto. (La flecha se omite si las raíces tienen la misma longitud.) Pensando en la flecha como un signo "más grande que" lo deja claro de qué manera debe ir la flecha. Los diagramas de Dynkin conducen a una clasificación de los sistemas de raíz. Los ángulos y las relaciones de longitud entre las raíces están relacionados. Así, los bordes para raíces no ortogonales pueden describirse alternativamente como un borde para una relación de longitud de 1, dos bordes para una relación de longitud de ${sqrt {2}}$ , y tres bordes para una relación de longitud ${sqrt {3}}$ . (No hay bordes cuando las raíces son ortogonales, independientemente de la relación longitud.)

En el $A_{2}$ sistema raíz, mostrado a la derecha, las raíces etiquetadas $alpha$ y $beta$ formar una base. Dado que estas dos raíces están en ángulo de 120 grados (con una relación de longitud de 1), el diagrama de Dynkin consta de dos vértices conectados por un solo borde: .

Restricciones

Los diagramas de Dynkin deben satisfacer ciertas restricciones; estos son esencialmente los que satisfacen los diagramas finitos de Coxeter-Dynkin, junto con una restricción cristalográfica adicional.

Conexión con diagramas de Coxeter

Los diagramas de Dynkin están estrechamente relacionados con los diagramas de Coxeter de grupos de Coxeter finitos, y la terminología a menudo se confunde.

Los diagramas de Dynkin difieren de los diagramas de Coxeter de grupos finitos en dos aspectos importantes:

Dirigido parcialmente: Los diagramas de Dynkin son parcialmente dirigida – cualquier borde múltiple (en términos de Coxeter, etiquetado con "4" o superior) tiene una dirección (una flecha apuntando de un nodo a otro); por lo tanto, los diagramas de Dynkin tienen más datos que el diagrama de Coxeter subyacente (gráfico no dirigido).; En el nivel de sistemas de raíces la dirección corresponde a apuntar hacia el vector más corto; los bordes etiquetados "3" no tienen dirección porque los vectores correspondientes deben tener igual longitud. (Caución: Algunos autores revierten esta convención, con la flecha apuntando hacia el vector más largo.)
Restricciones cristalográficas: Los diagramas de Dynkin deben satisfacer una restricción adicional, es decir, que las únicas etiquetas de borde permitido son 2, 3, 4 y 6, una restricción no compartida por los diagramas de Coxeter, así que no todos los diagramas de Coxeter de un grupo finito provienen de un diagrama de Dynkin.; En el nivel de los sistemas raíz esto corresponde al teorema de restricción cristalográfica, ya que las raíces forman una celosía.

Otra diferencia, que es solo estilística, es que los diagramas de Dynkin se dibujan convencionalmente con bordes dobles o triples entre nodos (para p = 4, 6), en lugar de un borde etiquetado con &# 34;p".

El término "diagrama de Dynkin" a veces se refiere al gráfico dirigido, a veces al gráfico no dirigido. Para mayor precisión, en este artículo "Diagrama de Dynkin" significará dirigido y el gráfico subyacente no dirigido se denominará "diagrama de Dynkin no dirigido". Entonces los diagramas de Dynkin y los diagramas de Coxeter se pueden relacionar de la siguiente manera:

	cristalográfica	grupo de puntos
Dirigida	Diagramas de dinkin
no redirigido	diagramas de Dynkin no dirigidos	Coxeter diagramas de grupos finitos

Con esto se quiere decir que los diagramas de Coxeter de grupos finitos corresponden a grupos puntuales generados por reflexiones, mientras que los diagramas de Dynkin deben satisfacer una restricción adicional correspondiente al teorema de restricción cristalográfica, y que los diagramas de Coxeter son no dirigidos, mientras que los diagramas de Dynkin son (parcialmente) dirigido.

Los objetos matemáticos correspondientes clasificados por los diagramas son:

	cristalográfica	grupo de puntos
Dirigida	root systems
no redirigido	Grupos de Weyl	grupos finitos de Coxeter

El espacio en blanco en la parte superior derecha, correspondiente a gráficos dirigidos con un gráfico no dirigido subyacente a cualquier diagrama de Coxeter (de un grupo finito), se puede definir formalmente, pero se discute poco y no parece admitir una interpretación simple en términos de objetos matemáticos de interés.

Hay mapas naturales hacia abajo, desde diagramas de Dynkin hasta diagramas de Dynkin no dirigidos; respectivamente, de los sistemas de raíces a los grupos de Weyl asociados, y a la derecha, de los diagramas de Dynkin no dirigidos a los diagramas de Coxeter; respectivamente de grupos Weyl a grupos finitos de Coxeter.

El mapa descendente es sobre (por definición) pero no uno a uno, como B_n y C Los diagramas _n corresponden al mismo diagrama no dirigido, con el diagrama de Coxeter resultante y el grupo de Weyl, por lo tanto, a veces denominados BC_n.

El mapa correcto es simplemente una inclusión: los diagramas de Dynkin no dirigidos son casos especiales de diagramas de Coxeter, y los grupos de Weyl son casos especiales de grupos de Coxeter finitos, y no es correcto, ya que no todos los diagramas de Coxeter son diagramas de Dynkin no dirigidos (el diagrama perdido los diagramas son H₃, H₄ y I₂(p) para p = 5 p ≥ 7), y correspondientemente no todo grupo finito de Coxeter es un grupo de Weyl.

Isomorfismos

Los diagramas de Dynkin son numerados convencionalmente para que la lista no sea redundante: $ngeq 1$ para $A_{n},$ $ngeq 2$ para $B_{n},$ $ngeq 3$ para $C_{n},$ $ngeq 4$ para $D_{n},$ y $E_{n}$ empezando $n=6.$ Sin embargo, las familias pueden definirse para menores No. ceder isomorfismos excepcionales de diagramas, y los isomorfismos excepcionales correspondientes de álgebras Lie y grupos asociados Lie.

Trivialmente, uno puede comenzar las familias en $n=0$ o $n=1,$ que son todos entonces isomorfos ya que hay un diagrama vacío único y un diagrama de 1-nodo único. Los otros isomorfismos de diagramas de Dynkin conectados son:

$A_{1}cong B_{1}cong C_{1}$
$B_{2}cong C_{2}$
$D_{2}cong A_{1}times A_{1}$
$D_{3}cong A_{3}$
$E_{3}cong A_{1}times A_{2}$
$E_{4}cong A_{4}$
$E_{5}cong D_{5}$

Estos isomorfismos corresponden a isomorfismos de álgebras de Lie simples y semisimples, que también corresponden a ciertos isomorfismos de formas grupales de Lie de estas. También agregan contexto a la familia En.

Automorfismos

El diagrama de Dynkin más simétrico es D₄, que da lugar a la prueba.

Además del isomorfismo entre diferentes diagramas, algunos diagramas también tienen autoisomorfismos o "automorfismos". Los automorfismos de diagrama corresponden a los automorfismos externos del álgebra de Lie, lo que significa que el grupo de automorfismos externos Out = Aut/Inn es igual al grupo de automorfismos de diagrama.

Los diagramas que tienen automorfismos no-triviales son A_n () $1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ ), D_n () $1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ ), y E₆. En todos estos casos excepto D₄, hay un único automorfismo no-trivial (Out = C₂, el grupo cíclico de orden 2), mientras que para D₄, el grupo automorfismo es el grupo simétrico en tres letras (S₃, orden 6) – este fenómeno se conoce como "juicio". Sucede que todos estos automorfismos de diagrama se pueden realizar como simetrías euclidianas de cómo los diagramas se dibujan convencionalmente en el plano, pero esto es sólo un artefacto de cómo se dibujan, y no estructura intrínseca.

A_n.

Para A_n, el automorfismo del diagrama está revirtiendo el diagrama, que es una línea. Los nodos del índice del diagrama son los pesos fundamentales, que (para A_n−1) $bigwedge ^{i}C^{n}$ para $i=1,dotsn$ , y el automorfismo del diagrama corresponde a la dualidad $bigwedge ^{i}C^{n}mapsto bigwedge ^{n-i}C^{n}.$ Realizado como el álgebra de Lie ${mathfrak {sl}}_{n+1},$ el automorfismo exterior se puede expresar como transpose negativo, $Tmapsto -T^{mathrm {T} }$ , que es cómo actúa la doble representación.

Para D_n, el automorfismo del diagrama está cambiando los dos nodos al final de la Y, y corresponde a cambiar las dos representaciones de giro chiral. Realizado como el álgebra de Lie ${mathfrak {so}}_{2n},$ el automorfismo externo se puede expresar como conjugación por una matriz en O(2n) con determinante −1. Cuando n = 3, uno tiene ${displaystyle mathrm {D} _{3}cong mathrm {A} _{3},}$ sus automorfismos están de acuerdo, mientras ${displaystyle mathrm {D} _{2}cong mathrm {A} _{1}times mathrm {A} _{1}}$ está desconectado, y el automorfismo corresponde a cambiar los dos nodos.

Para D₄, la representación fundamental es isomorfa a las dos representaciones de espín, y el grupo simétrico resultante en tres letras (S₃, o alternativamente el grupo diédrico de orden 6, Dih₃) corresponde tanto a los automorfismos del álgebra de Lie como a los automorfismos del diagrama.

E₆.

El grupo de automorfismos de E₆ corresponde a la inversión del diagrama y se puede expresar mediante álgebras de Jordan.

Los diagramas desconectados, que corresponden a álgebras de Lie semisimples, pueden tener automorfismos por el intercambio de componentes del diagrama.

En la característica 2, la flecha en F₄ puede ser ignorado, dando un automorfismo de diagrama adicional y grupos Suzuki-Ree correspondientes.

En la característica positiva hay "automorfismos diagramas adicionales" – aproximadamente hablando, en característica p a veces se permite ignorar la flecha en los lazos de la multiplicidad p en el diagrama de Dynkin cuando toma automorfismos de diagrama. Así en la característica 2 hay un orden 2 automorfismo de $mathrm {B} _{2}cong mathrm {C} _{2}$ and of F₄, mientras que en la característica 3 hay un orden 2 automorfismo de G₂. Pero no se aplica en todas las circunstancias: por ejemplo, tales automorfismos no deben surgir como automorfismos del grupo algebraico correspondiente, sino más bien en el nivel de puntos valorados en un campo finito.

Construcción de grupos de Lie mediante automorfismos de diagramas

Los automorfismos de diagrama a su vez producen grupos de Lie adicionales y grupos de tipo Lie, que son de importancia central en la clasificación de grupos simples finitos.

La construcción del grupo de Chevalley de los grupos de Lie en términos de su diagrama de Dynkin no produce algunos de los grupos clásicos, a saber, los grupos unitarios y los grupos ortogonales no divididos. Los grupos de Steinberg construyen los grupos unitarios ²A_n, mientras que los otros grupos ortogonales se construyen como ²D_n, donde en ambos casos esto se refiere a combinar un automorfismo de diagrama con un automorfismo de campo. Esto también produce grupos de Lie exóticos adicionales ²E₆ y ³D₄, este último solo definido sobre campos con un automorfismo de orden 3.

Los automorfismos de diagrama adicionales en característica positiva producen los grupos Suzuki-Ree, ²B₂, ²F₄ y ²G₂.

Plegado

Affine Coxeter grupo plegables, con tres convenciones de nominación: primero, el conjunto original extendido; el segundo utilizado en el contexto de los gráficos del quiver; y el último por Victor Kac para áfina torcida Lie álgebras.

Un diagrama de Dynkin (simplemente entrelazado) (finito o afín) que tiene una simetría (que satisface una condición, a continuación) puede ser cociente por la simetría, produciendo un nuevo diagrama generalmente enlazado de forma múltiple, con el proceso llamado plegado (debido a que la mayoría de las simetrías son dobles). En el nivel de las álgebras de Lie, esto corresponde a tomar la subálgebra invariante bajo el grupo de automorfismos externos, y el proceso puede definirse puramente con referencia a los sistemas de raíces, sin usar diagramas. Además, todos los diagramas de enlaces múltiples (finitos o infinitos) se pueden obtener doblando un diagrama de enlaces simples.

La única condición del automorfismo para que sea posible el plegamiento es que los distintos nodos del gráfico en la misma órbita (bajo el automorfismo) no deben estar conectados por un borde; a nivel de sistemas de raíces, las raíces en la misma órbita deben ser ortogonales. A nivel de diagramas, esto es necesario ya que, de lo contrario, el diagrama de cociente tendrá un bucle, debido a que identifica dos nodos pero tiene un borde entre ellos, y los bucles no están permitidos en los diagramas de Dynkin.

Los nodos y las aristas del diagrama del cociente ("doblado") son las órbitas de los nodos y las aristas del diagrama original; los bordes son únicos a menos que dos bordes incidentes se correspondan con el mismo borde (especialmente en nodos de valencia mayores que 2): un "punto de ramificación" del mapa, en cuyo caso el peso es el número de aristas incidentes, y la flecha apunta hacia el nodo en el que inciden: "el punto de bifurcación se asigna al punto no homogéneo& #34;. Por ejemplo, en D₄ doblando a G₂, el borde en G₂ apunta desde la clase de los 3 nodos exteriores (valencia 1), a la clase del nodo central (valencia 3).

Los plegamientos de diagramas finitos son:

$A_{2n-1}to C_{n}$

(El automorfismo de A_2n no produce un plegado porque los dos nodos intermedios están conectados por un borde, pero en la misma órbita.)

$D_{n+1}to B_{n}$
$D_{4}to G_{2}$ (si se cita por el grupo completo o un 3 ciclo, además de $D_{4}to B_{3}$ de tres maneras diferentes, si se orienta por una involución)
$E_{6}to F_{4}$

Existen pliegues similares para diagramas afines, que incluyen:

${tilde {A}}_{2n-1}to {tilde {C}}_{n}$
${tilde {D}}_{n+1}to {tilde {B}}_{n}$
${tilde {D}}_{4}to {tilde {G}}_{2}$
${tilde {E}}_{6}to {tilde {F}}_{4}$

La noción de pliegues también se puede aplicar de manera más general a los diagramas de Coxeter; en particular, se pueden generalizar los cocientes permitidos de los diagramas de Dynkin a H_n e I₂(p). Geométricamente esto corresponde a proyecciones de politopos uniformes. En particular, cualquier diagrama de Dynkin simplemente entrelazado se puede plegar a I₂(h), donde h es el número de Coxeter, que corresponde geométricamente a la proyección al plano de Coxeter.

El plegado se puede aplicar para reducir preguntas sobre álgebras de Lie (semisimples) a preguntas sobre álgebras entrelazadas simples, junto con un automorfismo, que puede ser más simple que tratar directamente álgebras entrelazadas múltiples; esto se puede hacer al construir las álgebras de Lie semisimples, por ejemplo. Consulte Desbordamiento matemático: plegado por automorfismos para obtener más información.

Otros mapas de diagramas

A₂ root system	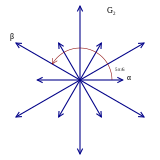G₂ root system

Algunos mapas adicionales de diagramas tienen interpretaciones significativas, como se detalla a continuación. Sin embargo, no todos los mapas de sistemas raíz surgen como mapas de diagramas.

Por ejemplo, hay dos inclusiones de sistemas de raíces de A₂ en G₂, ya sea como las seis raíces largas o las seis raíces cortas. Sin embargo, los nodos en el diagrama G₂ corresponden a una raíz larga y una raíz corta, mientras que los nodos en el diagrama A₂ corresponden a raíces de igual longitud, y por lo tanto este mapa de sistemas raíz no puede expresarse como un mapa de los diagramas.

Algunas inclusiones de sistemas raíz se pueden expresar como un diagrama que es un subgráfico inducido de otro, lo que significa "un subconjunto de los nodos, con todos los bordes entre ellos". Esto se debe a que eliminar un nodo de un diagrama de Dynkin equivale a eliminar una raíz simple de un sistema de raíces, lo que produce un sistema de raíces de rango uno inferior. Por el contrario, eliminar una arista (o cambiar la multiplicidad de una arista) y dejar los nodos sin cambios corresponde a cambiar los ángulos entre las raíces, lo que no se puede hacer sin cambiar todo el sistema de raíces. Por lo tanto, uno puede eliminar nodos de manera significativa, pero no bordes. Eliminar un nodo de un diagrama conexo puede producir un diagrama conexo (álgebra de Lie simple), si el nodo es una hoja, o un diagrama desconectado (álgebra de Lie semisimple pero no simple), con dos o tres componentes (el último para D_n y E_n). A nivel de álgebras de Lie, estas inclusiones corresponden a sub-álgebras de Lie.

Los subgráficos máximos son los siguientes; los subgrafos relacionados por un automorfismo de diagrama se etiquetan como "conjugado":

A_{n+ 1}A_n, en 2 formas conjugadas.
B_{n+ 1}A_n, B_n.
C_{n+ 1}A_n, C_n.
D_{n+ 1}A_n (2 formas conjugadas), D_n.
E_{n+ 1}A_n, D_n, E_n.
- Para E₆, dos de ellos coinciden: $mathrm {D} _{5}cong mathrm {E} _{5}$ y son conjugados.
F₄B₃, C₃.
G₂A₁, en 2 formas no conjugadas (como una raíz larga o una raíz corta).

Finalmente, la dualidad de diagramas corresponde a invertir la dirección de las flechas, si las hay: B_n y C_n son duales, mientras que F₄ y G₂ son autoduales, al igual que los diagramas ADE de enlace simple.

Simplemente atada

(feminine)

Un diagrama de Dynkin sin múltiples bordes se llama simplemente lavado, como son el correspondiente Álgebra de Lie y el grupo Lie. Estos son los $A_{n},D_{n},E_{n}$ diagramas, y fenómenos que tales diagramas clasifican se denominan clasificación ADE. En este caso los diagramas de Dynkin coinciden exactamente con los diagramas de Coxeter, ya que no hay múltiples bordes.

Diagramas Satake

Los diagramas de Dynkin clasifican álgebras de Lie complejas semisimples. Las álgebras de Lie semisimples reales se pueden clasificar como formas reales de álgebras de Lie semisimples complejas, y se clasifican mediante diagramas de Satake, que se obtienen del diagrama de Dynkin etiquetando algunos vértices de negro (rellenos) y conectando algunos otros vértices en pares mediante flechas. de acuerdo con ciertas reglas.

Historia

Los diagramas de Dynkin llevan el nombre de Eugene Dynkin, quien los usó en dos artículos (1946, 1947) para simplificar la clasificación de álgebras de Lie semisimples; ver (Dynkin 2000). Cuando Dynkin abandonó la Unión Soviética en 1976, lo que en ese momento se consideraba equivalente a una traición, se ordenó a los matemáticos soviéticos que se refirieran a "diagramas de raíces simples" en lugar de usar su nombre.

Coxeter (1934) había utilizado anteriormente gráficos no dirigidos para clasificar los grupos de reflexión, donde los nodos correspondían a reflexiones simples; luego Witt (1941) usó los gráficos (con información de longitud) en referencia a los sistemas de raíces, con los nodos correspondientes a raíces simples, como se usan hoy. Dynkin luego los usó en 1946 y 1947, reconociendo a Coxeter y Witt en su artículo de 1947.

Convenios

Los diagramas de Dynkin se han dibujado de varias maneras; la convención seguida aquí es común, con ángulos de 180° en los nodos de valencia 2, ángulos de 120° en el nodo de valencia 3 de D_n, y 90°/90°/ Ángulos de 180° en el nodo de valencia 3 de E_n, con la multiplicidad indicada por 1, 2 o 3 aristas paralelas, y la longitud de la raíz indicada dibujando una flecha en la arista para orientación. Más allá de la simplicidad, otro beneficio de esta convención es que los automorfismos de los diagramas se realizan mediante isometrías euclidianas de los diagramas.

La convención alternativa incluye escribir un número en el borde para indicar multiplicidad (comúnmente usado en los diagramas de Coxeter), oscurecer los nodos para indicar la longitud de la raíz o usar ángulos de 120° en los nodos de valencia 2 para que los nodos sean más distintos.

También existen convenciones sobre la numeración de los nodos. La convención moderna más común se había desarrollado en la década de 1960 y se ilustra en (Bourbaki 1968).

Diagramas de Dynkin de rango 2

Los diagramas de Dynkin son equivalentes a las matrices de Cartan generalizadas, como se muestra en esta tabla de diagramas de Dynkin de rango 2 con sus correspondientes matrices de Cartan 2x2.

Para el rango 2, la forma de matriz de Cartan es:

A=left[{begin{matrix}2&a_{12}\a_{21}&2end{matrix}}right]

Un diagrama de múltiples aristas corresponde a los elementos de matriz de Cartan no diagonales -a₂₁, -a₁₂, con el número de aristas dibujadas igual a max(-a₂₁, -a₁₂), y una flecha que apunta hacia los elementos que no son de unidad.

A matriz Cartan generalizada es una matriz cuadrada $A=(a_{ij})$ tal que:

Para entradas diagonales, $a_{ii}=2$ .
Para entradas no diagonales, $a_{ij}leq 0$ .
$a_{ij}=0$ si $a_{ji}=0$

La matriz de Cartan determina si el grupo es de tipo finito (si es una matriz definida positiva, es decir, todos los valores propios son positivos), de tipo afín (si no es positivo-definido sino positivo-semidefinido, es decir, todos los valores propios son no negativos), o de tipo indefinido. El tipo indefinido a menudo se subdivide aún más, por ejemplo, un grupo de Coxeter es lorentziano si tiene un valor propio negativo y todos los demás valores propios son positivos. Además, múltiples fuentes se refieren a grupos de Coxeter hiberbólicos, pero hay varias definiciones no equivalentes para este término. En la discusión a continuación, los grupos de Coxeter hiperbólicos son un caso especial de Lorentzian, que satisface una condición adicional. Para el rango 2, todas las matrices de Cartan determinantes negativos corresponden al grupo hiperbólico de Coxeter. Pero, en general, la mayoría de las matrices de determinantes negativos no son ni hiperbólicas ni lorentzianas.

Las ramas finitas tienen (-a₂₁, -a₁₂)=(1,1), (2,1), (3,1) y afines las ramas (con determinante cero) tienen (-a₂₁, -a₁₂) =(2,2) o (4,1).

diagramas Rank 2 Dynkin
Grupo Nombre	Dynkin diagram			Matriz de Cartan		Simmetría orden	Relacionados simplemente lavado grupo³
Grupo Nombre	(Standard) multiedge Gráfico	Valorado Gráfico¹	Coxeter Gráfico²	$left[{begin{matrix}2&a_{12}\a_{21}&2end{matrix}}right]$	Determinante (4 a)₂₁*a₁₂)	Simmetría orden	Relacionados simplemente lavado grupo³
Finite (Determinant conviene0)
A₁xA₁				$left[{begin{smallmatrix}2&0\0&2end{smallmatrix}}right]$	4	2
A₂ (sin dirección)				$left[{begin{smallmatrix}2&-1\-1&2end{smallmatrix}}right]$	3	3
B₂				$left[{begin{smallmatrix}2&-2\-1&2end{smallmatrix}}right]$	2	4	${A}_{3}$
C₂				$left[{begin{smallmatrix}2&-1\-2&2end{smallmatrix}}right]$	2	4	${A}_{3}$
BC₂ (sin dirección)				$left[{begin{smallmatrix}2&-{sqrt {2}}\-{sqrt {2}}&2end{smallmatrix}}right]$	2	4
G₂				$left[{begin{smallmatrix}2&-1\-3&2end{smallmatrix}}right]$	1	6	${D}_{4}$
G₂ (sin dirección)				$left[{begin{smallmatrix}2&-{sqrt {3}}\-{sqrt {3}}&2end{smallmatrix}}right]$	1	6
Affine (Determinant=0)
A₁¹⁾				$left[{begin{smallmatrix}2&-2\-2&2end{smallmatrix}}right]$	0	JUEGO	${tilde {A}}_{3}$
A₂²⁾				$left[{begin{smallmatrix}2&-1\-4&2end{smallmatrix}}right]$	0	JUEGO	${tilde {D}}_{4}$
Hiperbólico (Determinante realizado0)
				$left[{begin{smallmatrix}2&-1\-5&2end{smallmatrix}}right]$	-1	-
				$left[{begin{smallmatrix}2&-2\-3&2end{smallmatrix}}right]$	-2	-
				$left[{begin{smallmatrix}2&-1\-6&2end{smallmatrix}}right]$	-2	-
				$left[{begin{smallmatrix}2&-1\-7&2end{smallmatrix}}right]$	-3	-
				$left[{begin{smallmatrix}2&-2\-4&2end{smallmatrix}}right]$	-4	-
				$left[{begin{smallmatrix}2&-1\-8&2end{smallmatrix}}right]$	-4	-
				$left[{begin{smallmatrix}2&-3\-3&2end{smallmatrix}}right]$	-5	-
				$left[{begin{smallmatrix}2&-b\-a&2end{smallmatrix}}right]$	4-ab	-
Nota¹: Para grupos hiperbólicos, (a₁₂*a₂₁√4), el estilo multiedge se abandona a favor de un etiquetado explícito (a₂₁, a₁₂En el borde. Estos generalmente no se aplican a gráficos finitos y afinados. Nota²: Para grupos no dirigidos, los diagramas de Coxeter son intercambiables. Por lo general son etiquetados por su orden de simetría, con el orden-3 implícito sin etiqueta. Nota³: Muchos grupos multiedge pueden obtenerse de un grupo de rango superior simplemente lavado aplicando una operación plegable adecuada.

Diagramas finitos de Dynkin

Gráficos Finite Dynkin con 1 a 9 nodos
Rank	Clásico Grupos de mentira				Excepcional Grupos de mentira
Rank	${A}_{1+}$	${B}_{2+}$	${C}_{2+}$	${D}_{2+}$	${E}_{3-8}$	${G}_{2}$ / ${F}_{4}$
1	A₁
2	A₂	B₂	C₂= B₂	D₂= A₁A₁		G₂
3	A₃	B₃	C₃	D₃= A₃	E₃= A₂A₁
4	A₄	B₄	C₄	D₄	E₄= A₄	F₄
5	A₅	B₅	C₅	D₅	E₅= D₅
6	A₆	B₆	C₆	D₆	E₆
7	A₇	B₇	C₇	D₇	E₇
8	A₈	B₈	C₈	D₈	E₈
9	A₉	B₉	C₉	D₉
10+	..	..	..	..

Diagramas de Dynkin afines

Hay extensiones de diagramas de Dynkin, a saber, los diagramas affine Dynkin; estos clasificar matrices de Cartan de affine Álgebras de Lie. These are classified in (Kac 1994, Chapter 4, pp. 47–), specifically listed on (Kac 1994, pp. 53–55). Los diagramas de Affine se denotan como $X_{l}^{(1)},X_{l}^{(2)},$ o $X_{l}^{(3)},$ Donde X es la letra del diagrama finito correspondiente, y el exponente depende de qué serie de diagramas de afine están en. El primero de ellos, $X_{l}^{(1)},$ son más comunes, y se llaman diagramas de Dynkin extendidos y denotado con un tilde, y también a veces marcado con un + superscript. como en ${tilde {A}}_{5}=A_{5}^{(1)}=A_{5}^{+}$ . Las series (2) y (3) se denominan diagramas de afina retorcidos.

Consulte el generador de diagramas de Dynkin para obtener diagramas.

El conjunto de diagramas de afina extendida Dynkin, con nodos añadidos en verde ( $ngeq 3$ para $B_{n}$ y $ngeq 4$ para $D_{n}$ )	Las formas de affine "Twisted" son nombradas con (2) o (3) superscripts. (El subscripto) k siempre cuenta el número de amarillo nodos en el gráfico, es decir, el número total de nodos menos 1.)

Aquí están todos los gráficos de Dynkin para grupos afines de hasta 10 nodos. Los gráficos de Dynkin extendidos se dan como las familias ~, al igual que los gráficos finitos anteriores, con un nodo agregado. Otras variaciones de gráficos dirigidos se dan con un valor de superíndice (2) o (3), que representan plegamientos de grupos de orden superior. Estos se clasifican como diagramas Afines retorcidos.

Gráficos Affine Dynkin conectados hasta (2 a 10 nodos)
(Grouped as undirected graphs)
Rank	${tilde {A}}_{1+}$	${tilde {B}}_{3+}$	${tilde {C}}_{2+}$	${tilde {D}}_{4+}$	E / F / G
2	${tilde {A}}_{1}$ o ${A}_{1}^{(1)}$		${A}_{2}^{(2)}$ :
3	${tilde {A}}_{2}$ o ${A}_{2}^{(1)}$		${tilde {C}}_{2}$ o ${C}_{2}^{(1)}$ ${D}_{5}^{(2)}$ : ${A}_{4}^{(2)}$ :		${tilde {G}}_{2}$ o ${G}_{2}^{(1)}$ ${D}_{4}^{(3)}$
4	${tilde {A}}_{3}$ o ${A}_{3}^{(1)}$	${tilde {B}}_{3}$ o ${B}_{3}^{(1)}$ ${A}_{5}^{(2)}$ :	${tilde {C}}_{3}$ o ${C}_{3}^{(1)}$ ${D}_{6}^{(2)}$ : ${A}_{6}^{(2)}$ :
5	${tilde {A}}_{4}$ o ${A}_{4}^{(1)}$	${tilde {B}}_{4}$ o ${B}_{4}^{(1)}$ ${A}_{7}^{(2)}$ :	${tilde {C}}_{4}$ o ${C}_{4}^{(1)}$ ${D}_{7}^{(2)}$ : ${A}_{8}^{(2)}$ :	${tilde {D}}_{4}$ o ${D}_{4}^{(1)}$	${tilde {F}}_{4}$ o ${F}_{4}^{(1)}$ ${E}_{6}^{(2)}$
6	${tilde {A}}_{5}$ o ${A}_{5}^{(1)}$	${tilde {B}}_{5}$ o ${B}_{5}^{(1)}$ ${A}_{9}^{(2)}$ :	${tilde {C}}_{5}$ o ${C}_{5}^{(1)}$ ${D}_{8}^{(2)}$ : ${A}_{10}^{(2)}$ :	${tilde {D}}_{5}$ o ${D}_{5}^{(1)}$
7	${tilde {A}}_{6}$ o ${A}_{6}^{(1)}$	${tilde {B}}_{6}$ o ${B}_{6}^{(1)}$ ${A}_{11}^{(2)}$ :	${tilde {C}}_{6}$ o ${C}_{6}^{(1)}$ ${D}_{9}^{(2)}$ : ${A}_{12}^{(2)}$ :	${tilde {D}}_{6}$ o ${D}_{6}^{(1)}$	${tilde {E}}_{6}$ o ${E}_{6}^{(1)}$
8	${tilde {A}}_{7}$ o ${A}_{7}^{(1)}$	${tilde {B}}_{7}$ o ${B}_{7}^{(1)}$ ${A}_{13}^{(2)}$ :	${tilde {C}}_{7}$ o ${C}_{7}^{(1)}$ ${D}_{10}^{(2)}$ : ${A}_{14}^{(2)}$ :	${tilde {D}}_{7}$ o ${D}_{7}^{(1)}$	${tilde {E}}_{7}$ o ${E}_{7}^{(1)}$
9	${tilde {A}}_{8}$ o ${A}_{8}^{(1)}$	${tilde {B}}_{8}$ o ${B}_{8}^{(1)}$ ${A}_{15}^{(2)}$ :	${tilde {C}}_{8}$ o ${C}_{8}^{(1)}$ ${D}_{11}^{(2)}$ : ${A}_{16}^{(2)}$ :	${tilde {D}}_{8}$ o ${D}_{8}^{(1)}$	${tilde {E}}_{8}$ o ${E}_{8}^{(1)}$
10	${tilde {A}}_{9}$ o ${A}_{9}^{(1)}$	${tilde {B}}_{9}$ o ${B}_{9}^{(1)}$ ${A}_{17}^{(2)}$ :	${tilde {C}}_{9}$ o ${C}_{9}^{(1)}$ ${D}_{12}^{(2)}$ : ${A}_{18}^{(2)}$ :	${tilde {D}}_{9}$ o ${D}_{9}^{(1)}$
11	...	...	...	...

Diagramas de Dynkin hiperbólicos y superiores

Se ha enumerado el conjunto de gráficos de Dynkin hiperbólicos compactos y no compactos. Todos los gráficos hiperbólicos de rango 3 son compactos. Los diagramas de Dynkin hiperbólicos compactos existen hasta el rango 5 y los gráficos hiperbólicos no compactos existen hasta el rango 10.

Resumen
Rank	Compacto	No	Total
3	31	93	123
4	3	50	53
5	1	21	22
6	0	22	22
7	0	4	4
8	0	5	5
9	0	5	5
10	0	4	4

Diagramas de Dynkin hiperbólicos compactos

Gráficos hiperbólicos compactos
Rank 3		Rank 4	Rank 5
Gráficos lineales (6 4 2): H₁₀₀³⁾: H₁₀₁³⁾: H₁₀₅³⁾: H₁₀₆³⁾: (6 6 2): H₁₁₄³⁾: H₁₁₅³⁾: H₁₁₆³⁾:	Gráficos cólicos (4 3 3): H₁³⁾: (4 4 3): 3 formas... (4 4 4): 2 formas... (6 3 3): H₃³⁾: (6 4 3): 4 formas... (6 4 4): 4 formas... (6 6 3): 3 formas... (6 6 4): 4 formas... (6 6 6): 2 formas...	(4 3 3 3): H₈⁴⁾: H₁₃⁴⁾: (4 3 4 3): H₁₄⁴⁾:	(4 3 3 3 3): H₇⁵⁾:

Did you mean:

Non Compact (Over-extended forms)

Algunas notaciones utilizadas en física teórica, como la teoría M, utilizan un signo "+" superíndice para grupos extendidos en lugar de un "~" y esto permite definir grupos de extensiones superiores.

Extended Los diagramas de Dynkin (affine) se dan "+" y representan un nodo añadido. (Lo mismo como "~")
Gastos generales Los diagramas de Dynkin (hiperbólicos) se dan "^" o "++" y representan dos nodos añadidos.
Muy extendido Los diagramas de Dynkin con 3 nodos añadidos se dan "+++".

Algunos ejemplos de diagramas de Dynkin sobreextended (hiperbólicos)
Rank	${AE}_{n}$ = A_n-2^{(1)^}	${BE}_{n}$ B_n-2^{(1)^} ${CE}_{n}$	C_n-2^{(1)^}	${DE}_{n}$ D_n-2^{(1)^}	E / F / G
3	${AE}_{3}$ :
4	${AE}_{4}$ :		C₂^{(1)^} A₄^{(2)'^} A₄^{2)^} D₃^{2)^}		G₂^{(1)^} D₄^{(3)^}
5	${AE}_{5}$ :	${BE}_{5}$ ${CE}_{5}$	C₃^{(1)^} A₆^{2)^} A₆^{(2)'^} D₅^{2)^}
6	${AE}_{6}$	${BE}_{6}$ ${CE}_{6}$	C₄^{(1)^} A₈^{2)^} A₈^{(2)'^} D₇^{2)^}	${DE}_{6}$	F₄^{(1)^} E₆^{2)^}
7	${AE}_{7}$	${BE}_{7}$ ${CE}_{7}$		${DE}_{7}$
8	${AE}_{8}$	${BE}_{8}$ ${CE}_{8}$		${DE}_{8}$	E₆^{(1)^}
9	${AE}_{9}$	${BE}_{9}$ ${CE}_{9}$		${DE}_{9}$	E₇^{(1)^}
10		${BE}_{10}$ ${CE}_{10}$		${DE}_{10}$	${E}_{10}$ = E₈^{(1)^}

238 Grupos hiperbólicos (compactos y no compactos)

Los 238 grupos hiperbólicos (compactados y no compactados) de rango $ngeq 3$ son nombrados ${displaystyle H_{i}^{(n)}}$ y enumeradas como ${displaystyle i=1,2,3...}$ por cada rango.

Muy extendido

Los grupos muy extendidos son grupos de Lorentz, definidos al agregar tres nodos a los grupos finitos. El E₈, E₇, E₆, F₄ y G₂ ofrecen seis series que terminan en grupos muy extensos. Otras series extendidas que no se muestran se pueden definir desde A_n, B_n, C_n y D_n, como series diferentes para cada n. El determinante de la matriz de Cartan asociada determina dónde cambia la serie de finito (positivo) a afín (cero) a un grupo hiperbólico no compacto (negativo), y termina como un grupo de Lorentz que se puede definir con el uso de una dimensión similar al tiempo, y se utiliza en la teoría M.

Serie ampliada Rank 2
Finite	$A_{2}$	$C_{2}$	$G_{2}$
2	A₂	C₂	G₂
3	A₂⁺= ${tilde {A}}_{2}$	C₂⁺= ${tilde {C}}_{2}$	G₂⁺= ${tilde {G}}_{2}$
4	A₂⁺⁺	C₂⁺⁺	G₂⁺⁺
5	A₂⁺⁺	C₂⁺⁺	G₂⁺⁺
Det(M_n)	3(3-n)	2(3-n)	3-n

Rank 3 y 4 series extendidas
Finite	$A_{3}$	$B_{3}$	$C_{3}$	$A_{4}$	$B_{4}$	$C_{4}$	$D_{4}$	$F_{4}$
2		A₁²						A₂
3	A₃	B₃	C₃		B₂A₁		A₁³
4	A₃⁺= ${tilde {A}}_{3}$	B₃⁺= ${tilde {B}}_{3}$	C₃⁺= ${tilde {C}}_{3}$	A₄	B₄	C₄	D₄	F₄
5	A₃⁺⁺	B₃⁺⁺	C₃⁺⁺	A₄⁺= ${tilde {A}}_{4}$	B₄⁺= ${tilde {B}}_{4}$	C₄⁺= ${tilde {C}}_{4}$	D₄⁺= ${tilde {D}}_{4}$	F₄⁺= ${tilde {F}}_{4}$
6	A₃⁺⁺	B₃⁺⁺	C₃⁺⁺	A₄⁺⁺	B₄⁺⁺	C₄⁺⁺	D₄⁺⁺	F₄⁺⁺
7				A₄⁺⁺	B₄⁺⁺	C₄⁺⁺	D₄⁺⁺	F₄⁺⁺
Det(M_n)	4(4-n)	2(4-n)		5(5-n)	2(5-n)		4(5-n)	5-n

Rank 5 y 6 series extendidas
Finite	$A_{5}$	$B_{5}$	$D_{5}$	$A_{6}$	$B_{6}$	$D_{6}$	$E_{6}$
4		B₃A₁	A₃A₁				A₂²
5	A₅		D₅		B₄A₁	D₄A₁	A₅
6	A₅⁺= ${tilde {A}}_{5}$	B₅⁺= ${tilde {B}}_{5}$	D₅⁺= ${tilde {D}}_{5}$	A₆	B₆	D₆	E₆
7	A₅⁺⁺	B₅⁺⁺	D₅⁺⁺	A₆⁺= ${tilde {A}}_{6}$	B₆⁺= ${tilde {B}}_{6}$	D₆⁺= ${tilde {D}}_{6}$	E₆⁺= ${tilde {E}}_{6}$
8	A₅⁺⁺	B₅⁺⁺	D₅⁺⁺	A₆⁺⁺	B₆⁺⁺	D₆⁺⁺	E₆⁺⁺
9				A₆⁺⁺	B₆⁺⁺	D₆⁺⁺	E₆⁺⁺
Det(M_n)	6(6-n)	2(6-n)	4(6-n)	7(7-n)	2(7-n)	4(7-n)	3(7-n)

Algunas categorías 7 y series más altas
Finite	A₇	B₇	D₇	E₇	E8
3					E₃= A₂A₁
4				A₃A₁	E₄= A₄
5				A₅	E₅= D₅
6		B₅A₁	D₅A₁	D₆	E₆
7	A₇	B₇	D₇	E₇	E₇
8	A₇⁺= ${tilde {A}}_{7}$	B₇⁺= ${tilde {B}}_{7}$	D₇⁺= ${tilde {D}}_{7}$	E₇⁺= ${tilde {E}}_{7}$	E₈
9	A₇⁺⁺	B₇⁺⁺	D₇⁺⁺	E₇⁺⁺	E₉= E₈⁺= ${tilde {E}}_{8}$
10	A₇⁺⁺	B₇⁺⁺	D₇⁺⁺	E₇⁺⁺	E₁₀= E₈⁺⁺
11					E₁₁= E₈⁺⁺
Det(M_n)	8(8-n)	2(8-n)	4(8-n)	2(8-n)	9-n

Contenido relacionado

Más resultados...