Diagrama de caja

En estadística descriptiva, un diagrama de caja o diagrama de caja es un método para demostrar gráficamente los grupos de localidad, dispersión y asimetría de datos numéricos a través de sus cuartiles. Además del cuadro en un gráfico de caja, puede haber líneas (que se denominan bigotes) que se extienden desde el cuadro indicando la variabilidad fuera de los cuartiles superior e inferior, por lo tanto, el gráfico también se denomina diagrama de caja y bigotes y el diagrama de caja y bigotes. Los valores atípicos que difieren significativamente del resto del conjunto de datos se pueden trazar como puntos individuales más allá de los bigotes en el diagrama de caja. Los diagramas de caja no son paramétricos: muestran la variación en las muestras de una población estadística sin hacer ninguna suposición de la distribución estadística subyacente (aunque el diagrama de caja de Tukey asume simetría para los bigotes y normalidad para su longitud). Los espacios en cada subsección del diagrama de caja indican el grado de dispersión (propagación) y asimetría de los datos, que generalmente se describen utilizando el resumen de cinco números. Además, el diagrama de caja permite estimar visualmente varios estimadores L, en particular el rango intercuartílico, la bisagra media, el rango, el rango medio y el trimean. Los diagramas de caja se pueden dibujar horizontal o verticalmente.

Historia

El método de la barra de rango fue introducido por primera vez por Mary Eleanor Spear en su libro "Charting Statistics" en 1952 y nuevamente en su libro "Técnicas prácticas de creación de gráficos" en 1969. El diagrama de caja y bigotes fue presentado por primera vez en 1970 por John Tukey, quien más tarde publicó sobre el tema en su libro "Análisis exploratorio de datos" en 1977.

Elementos

Un diagrama de caja es una forma estandarizada de mostrar el conjunto de datos en función del resumen de cinco números: el mínimo, el máximo, la mediana de la muestra y el primer y tercer cuartiles.

• MínimoQ₀ o el percentil 0: el punto de datos más bajo en el conjunto de datos excluyendo cualquier outliers
• Máximo (Q₄ o 100% percentil): el punto de datos más alto en el conjunto de datos excluyendo cualquier outliers
• MedianoQ₂ o 50 percentil): el valor medio en el conjunto de datos
• Primer cuartil (Q₁ o 25 percentil): también conocido como cuartil inferior q_n(0.25), es la mediana de la mitad inferior del conjunto de datos.
• Tercer cuartil (Q₃ o 75o percentil): también conocido como cuartil superior q_n(0.75), es la mediana de la mitad superior del conjunto de datos.

Además de los valores mínimo y máximo utilizados para construir un diagrama de caja, otro elemento importante que también se puede emplear para obtener un diagrama de caja es el rango intercuartílico (RIC), como se indica a continuación:

• Interquartile range (IQR): la distancia entre los cuartiles superiores e inferiores

IQR=Q3− − Q1=qn()0,75)− − qn()0,25){displaystyle {text{IQR}=Q_{3}-Q_{1}=q_{n}(0.75)-q_{n}(0.25)}

Wiskers

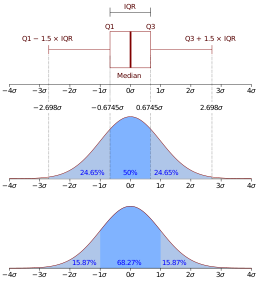
Un diagrama de caja generalmente incluye dos partes, una caja y un conjunto de bigotes, como se muestra en la Figura 2. La caja se dibuja desde Q₁ hasta Q₃ con una línea horizontal dibujada en el medio para indicar la mediana. Los bigotes deben terminar en un punto de datos observado, pero se pueden definir de varias maneras.

En el método más directo, el límite del bigote inferior es el valor mínimo del conjunto de datos y el límite del bigote superior es el valor máximo del conjunto de datos.

Otra opción popular para los límites de los bigotes se basa en el valor de 1,5 IQR. Desde arriba del cuartil superior (Q₃), se mide una distancia de 1,5 veces el IQR y se dibuja un bigote arriba al punto de datos observado más grande del conjunto de datos que se encuentra dentro de esta distancia. De manera similar, se mide una distancia de 1,5 veces el IQR por debajo del cuartil inferior (Q₁) y se dibuja un bigote hacia abajo al punto de datos observado más bajo del conjunto de datos que se encuentra dentro de esta distancia. Debido a que los bigotes deben terminar en un punto de datos observado, las longitudes de los bigotes pueden parecer desiguales, aunque 1,5 IQR sea el mismo para ambos lados. Todos los demás puntos de datos observados fuera del límite de los bigotes se trazan como valores atípicos. Los valores atípicos se pueden trazar en el diagrama de caja como un punto, un círculo pequeño, una estrella, etc. (vea el ejemplo a continuación).

Hay otras representaciones en las que los bigotes pueden representar varias otras cosas, como:

• El valor mínimo y máximo del conjunto de datos (como se muestra en la Figura 2)
• Una desviación estándar por encima y por debajo de la media del conjunto de datos
• El percentil 9 y el percentil 91 del conjunto de datos
• El segundo percentil y el percentil 98 del conjunto de datos

En raras ocasiones, el diagrama de caja se puede trazar sin los bigotes. Esto puede ser apropiado para información confidencial para evitar bigotes (y valores atípicos) que revelen los valores reales observados.

Algunos diagramas de caja incluyen un carácter adicional para representar la media de los datos.

Los percentiles inusuales 2 %, 9 %, 91 %, 98 % a veces se usan para tramas cruzadas de bigotes y extremos de bigotes para representar el resumen de siete números. Si los datos se distribuyen normalmente, las ubicaciones de las siete marcas en el diagrama de caja estarán igualmente espaciadas. En algunos diagramas de caja, se coloca una línea cruzada antes del final de cada bigote.

Debido a esta variabilidad, es apropiado describir la convención que se utiliza para los bigotes y los valores atípicos en el título del diagrama de caja.

Variaciones

Desde que el matemático John W. Tukey popularizó por primera vez este tipo de visualización de datos visuales en 1969, se han desarrollado varias variaciones del diagrama de caja clásico, y las dos variaciones más comunes son los diagramas de caja de ancho variable y los diagramas de caja con muescas. se muestra en la Figura 4.

Los gráficos de cuadro de ancho variable ilustran el tamaño de cada grupo cuyos datos se están representando haciendo que el ancho del cuadro sea proporcional al tamaño del grupo. Una convención popular es hacer que el ancho de la caja sea proporcional a la raíz cuadrada del tamaño del grupo.

Los gráficos de caja con muescas aplican una "muesca" o estrechamiento de la caja alrededor de la mediana. Las muescas son útiles para ofrecer una guía aproximada de la importancia de la diferencia de medianas; si las muescas de dos cajas no se superponen, esto proporcionará evidencia de una diferencia estadísticamente significativa entre las medianas. La altura de las muescas es proporcional al rango intercuartílico (RIC) de la muestra y es inversamente proporcional a la raíz cuadrada del tamaño de la muestra. Sin embargo, existe una incertidumbre sobre el multiplicador más adecuado (ya que este puede variar dependiendo de la similitud de las varianzas de las muestras). El ancho de la muesca se elige arbitrariamente para que sea agradable a la vista y debe ser coherente entre todos los diagramas de caja que se muestran en la misma página.

Una convención para obtener los límites de estas muescas es utilizar una distancia ± ± 1.58IQRn{displaystyle pm {frac {f} {fn} {fn}} {fn}}} {fn}}} {fn}}}} {fn}}}}} {fn}}}}}}}}}} {f}}}}}}}}}} {f}}}} alrededor de la mediana.

Los diagramas de caja ajustados están destinados a describir distribuciones sesgadas y se basan en la estadística de sesgo de la pareja media. Para un valor de par mediano de MC, las longitudes de los bigotes superior e inferior en el diagrama de caja se definen respectivamente como:

1,5IQR⋅ ⋅ e3MC,1,5IQR⋅ ⋅ e− − 4MCsiMC≥ ≥ 0,1,5IQR⋅ ⋅ e4MC,1,5IQR⋅ ⋅ e− − 3MCsiMC≤ ≤ 0.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

Para una distribución simétrica de datos, el medcouple será cero, y esto reduce el sistema ajustado de caja a la caja del Tukey con longitudes iguales de silbido 1,5IQR{displaystyle 1.5{text{ IQR}}} para ambos bigotes.

Otros tipos de diagramas de caja, como los diagramas de violín y los diagramas de frijol, pueden mostrar la diferencia entre distribuciones monomodales y multimodales, que no se pueden observar en el diagrama de caja clásico original.

Ejemplos

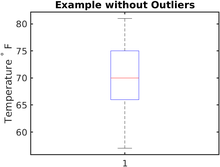
Ejemplo sin valores atípicos

Se midió una serie de temperaturas por hora a lo largo del día en grados Fahrenheit. Los valores registrados se enumeran en el siguiente orden (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.

Se puede generar un diagrama de caja del conjunto de datos calculando primero cinco valores relevantes de este conjunto de datos: mínimo, máximo, mediana (Q₂), primer cuartil (Q₁), y tercer cuartil (Q₃).

El mínimo es el número más pequeño del conjunto de datos. En este caso, la temperatura mínima registrada durante el día es de 57 °F.

El máximo es el mayor número del conjunto de datos. En este caso, la temperatura máxima registrada durante el día es de 81 °F.

La mediana es el "medio" número del conjunto de datos ordenado. Esto significa que hay exactamente el 50% de los elementos menor que la mediana y el 50% de los elementos mayor que la mediana. La mediana de este conjunto de datos ordenados es 70 °F.

El valor del primer cuartil (Q₁ o percentil 25) es el número que marca una cuarta parte de el conjunto de datos ordenado. En otras palabras, hay exactamente el 25% de los elementos que son menores que el primer cuartil y exactamente el 75% de los elementos que son mayores que él. El valor del primer cuartil se puede determinar fácilmente encontrando el "medio" número entre el mínimo y la mediana. Para las temperaturas horarias, el "medio" el número que se encuentra entre 57 °F y 70 °F es 66 °F.

El valor del tercer cuartil (Q₃ o percentil 75) es el número que marca las tres cuartas partes de el conjunto de datos ordenado. En otras palabras, hay exactamente un 75% de los elementos que están por debajo del tercer cuartil y un 25% de los elementos que están por encima de él. El valor del tercer cuartil se puede obtener fácilmente encontrando el "medio" número entre la mediana y el máximo. Para las temperaturas horarias, el "medio" número entre 70 °F y 81 °F es 75 °F.

El rango intercuartílico, o IQR, se puede calcular restando el valor del primer cuartil (Q₁) del valor del tercer cuartil (P₃):

IQR=Q3− − Q1=75∘ ∘ F− − 66∘ ∘ F=9∘ ∘ F.{displaystyle {text{IQR}=Q_{3}-Q_{1}=75^{circ }F-66^{circ }F=9^{circ }F}

Por lo tanto, 1,5IQR=1,5⋅ ⋅ 9∘ ∘ F=13.5∘ ∘ F.{displaystyle 1.5{text{IQR}=1.5cdot 9^{circ} }F=13.5^{circ }F.}

1,5 IQR por encima del tercer cuartil es:

Q3+1,5IQR=75∘ ∘ F+13.5∘ ∘ F=88,5∘ ∘ F.{displaystyle Q_{3}+1.5{text{ IQR}=75^{circ }F+13.5^{circ }F=88.5^{circ }F}

1,5 IQR por debajo del primer cuartil es:

Q1− − 1,5IQR=66∘ ∘ F− − 13.5∘ ∘ F=52,5∘ ∘ F.{displaystyle Q_{1}-1.5{text{ IQR}=66^{circ }F-13.5^{circ }F=52.5^{circ }F.}

El límite superior del bigote del diagrama de caja es el valor de datos más grande que está dentro de 1,5 IQR por encima del tercer cuartil. Aquí, 1,5 IQR por encima del tercer cuartil es 88,5 °F y el máximo es 81 °F. Por lo tanto, el bigote superior se dibuja en el valor del máximo, que es 81 °F.

Del mismo modo, el límite de bigotes inferior del diagrama de caja es el valor de datos más pequeño que está dentro de 1,5 IQR por debajo del primer cuartil. Aquí, 1,5 IQR por debajo del primer cuartil es 52,5 °F y el mínimo es 57 °F. Por lo tanto, el bigote inferior se dibuja al valor del mínimo, que es 57 °F.

Ejemplo con valores atípicos

Arriba hay un ejemplo sin valores atípicos. Aquí hay un ejemplo de seguimiento para generar un diagrama de caja con valores atípicos:

El conjunto ordenado para las temperaturas registradas es (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.

En este ejemplo, solo se cambian el primero y el último número. La mediana, el tercer cuartil y el primer cuartil siguen siendo los mismos.

En este caso, el valor máximo en este conjunto de datos es 89 °F y 1,5 IQR por encima del tercer cuartil es 88,5 °F. El máximo es superior a 1,5 IQR más el tercer cuartil, por lo que el máximo es un valor atípico. Por lo tanto, el bigote superior se dibuja en el valor mayor menor que 1.5 IQR por encima del tercer cuartil, que es 79 °F.

Del mismo modo, el valor mínimo en este conjunto de datos es 52 °F y 1,5 IQR por debajo del primer cuartil es 52,5 °F. El mínimo es menor que 1,5 IQR menos el primer cuartil, por lo que el mínimo también es un valor atípico. Por lo tanto, el bigote inferior se dibuja en el valor más pequeño superior a 1,5 IQR por debajo del primer cuartil, que es 57 °F.

En el caso de grandes conjuntos de datos

Un ejemplo adicional para obtener un diagrama de caja de un conjunto de datos que contiene una gran cantidad de puntos de datos es:

Ecuación general para calcular cuantiles empíricos

qn()p)=x()k)+α α ()x()k+1)− − x()k)){displaystyle q_{n}(p)=x_{(k)}+alpha (x_{(k+1)}-x_{(k)}}

conk=[p()n+1)]yα α =p()n+1)− − k{displaystyle {text{with }k=[p(n+1)]{text{ and }alpha =p(n+1)-k}

Aquí. x()k){displaystyle x_{(k)}} significa el orden general de los puntos de datos (es decir, si <math alttext="{displaystyle ii.k{displaystyle i wonK}<img alt="{displaystyle i, entonces <math alttext="{displaystyle x_{(i)}x()i).x()k){displaystyle x_{(i)}cantadox_{(k)}<img alt="{displaystyle x_{(i)})

Usando el ejemplo anterior que tiene 24 puntos de datos (n = 24), se puede calcular la mediana, el primer y el tercer cuartil de forma matemática o visual.

Mediano: qn()0.5)=x()12)+()0.5⋅ ⋅ 25− − 12)⋅ ⋅ ()x()13)− − x()12))=70+()0.5⋅ ⋅ 25− − 12)⋅ ⋅ ()70− − 70)=70∘ ∘ F{displaystyle q_{n}(0.5)=x_{(12)}+(0.5cdot 25-12)cdot (x_{(13)}-x_{(12)}=70+(0.5cdot 25-12)cdot (70-70)=70^{circ }F}

Primer cuartil: qn()0,25)=x()6)+()0,25⋅ ⋅ 25− − 6)⋅ ⋅ ()x()7)− − x()6))=66+()0,25⋅ ⋅ 25− − 6)⋅ ⋅ ()66− − 66)=66∘ ∘ F{displaystyle q_{n}(0.25)=x_{(6)}+(0.25cdot 25-6)cdot (x_{(7)}-x_{(6)})=66+(0.25cdot 25-6)cdot (66-66)=66^{circ }F}

Tercer cuartil: qn()0,75)=x()18)+()0,75⋅ ⋅ 25− − 18)⋅ ⋅ ()x()19)− − x()18))=75+()0,75⋅ ⋅ 25− − 18)⋅ ⋅ ()75− − 75)=75∘ ∘ F{displaystyle q_{n}(0.75)=x_{(18)}+(0.75cdot 25-18)cdot (x_{(19)}-x_{(18)})=75+(0.75cdot 25-18)cdot (75-75)=75^{circ }F}

Visualización

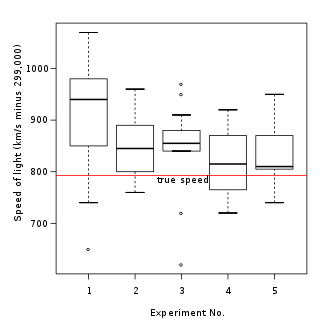
Aunque los diagramas de caja pueden parecer más primitivos que los histogramas o las estimaciones de densidad kernel, tienen una serie de ventajas. En primer lugar, el diagrama de caja permite a los estadísticos realizar un examen gráfico rápido de uno o más conjuntos de datos. Los diagramas de caja también ocupan menos espacio y, por lo tanto, son particularmente útiles para comparar distribuciones entre varios grupos o conjuntos de datos en paralelo (consulte la Figura 1 para ver un ejemplo). Por último, la estructura general de los histogramas y la estimación de la densidad del kernel pueden verse fuertemente influenciadas por la elección del número y el ancho de las técnicas de contenedores y la elección del ancho de banda, respectivamente.

Aunque mirar una distribución estadística es más común que mirar un diagrama de caja, puede ser útil comparar el diagrama de caja con la función de densidad de probabilidad (histograma teórico) para un N(0,σ²) y observar sus características directamente (como se muestra en la Figura 7).