Diagrama de bifurcación

En matemáticas, particularmente en sistemas dinámicos, un diagrama de bifurcación muestra los valores visitados o abordados asintóticamente (puntos fijos, órbitas periódicas o atractores caóticos) de un sistema en función de un parámetro de bifurcación en el sistema. Es habitual representar los valores estables con línea continua y los valores inestables con línea punteada, aunque a menudo se omiten los puntos inestables. Los diagramas de bifurcación permiten la visualización de la teoría de la bifurcación.

Animación que muestra la formación de un diagrama de bifurcación

diagrama de bifurcación del mapa del círculo. Las regiones negras corresponden a lenguas de Arnold.

Mapa logístico

Diagrama de bifurcación del mapa logístico. El atractivo para cualquier valor del parámetro r se muestra en la línea vertical en que r.

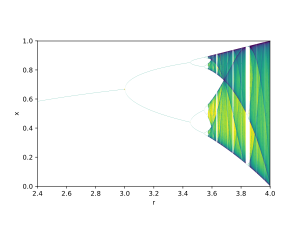
Un ejemplo es el diagrama de bifurcación del mapa logístico:

${displaystyle x_{n+1}=rx_{n}(1-x_{n},}$

El parámetro de bifurcación r se muestra en el eje horizontal del gráfico y el eje vertical muestra el conjunto de valores de la función logística visitada asintóticamente desde casi todas las condiciones iniciales.

El diagrama de bifurcación muestra la bifurcación de los períodos de órbitas estables de 1 a 2 a 4 a 8, etc. Cada uno de estos puntos de bifurcación es una bifurcación que duplica el período. La relación de las longitudes de los intervalos sucesivos entre los valores de r para los que se produce la bifurcación converge a la primera constante de Feigenbaum.

El diagrama también muestra duplicaciones de períodos de 3 a 6 a 12, etc., de 5 a 10 a 20, etc., y así sucesivamente.

Rotura de simetría en conjuntos de bifurcaciones

Simetría rompiendo en bifurcación de horquilla como parámetro ε es variado. ε= 0 es el caso de la bifurcación simétrica de horquilla.

En un sistema dinámico como

${displaystyle {ddot {x}+f(x;mu)+varepsilon g(x)=0,}$

que es estructuralmente estable cuando ${displaystyle mu neq 0}$, si se trama un diagrama de bifurcación, tratando ${displaystyle mu }$ como parámetro de bifurcación, pero para diferentes valores ${displaystyle varepsilon }$, el caso ${displaystyle varepsilon =0}$ es la bifurcación simétrica de horquilla. Cuando ${displaystyle varepsilon neq 0}$, decimos que tenemos un tenedor con Simetría rota. Esto se ilustra en la animación a la derecha.