Desvanecimiento de rayleigh

El desvanecimiento de Rayleigh es un modelo estadístico del efecto de un entorno de propagación en una señal de radio, como la que utilizan los dispositivos inalámbricos.

Los modelos de desvanecimiento de Rayleigh asumen que la magnitud de una señal que ha pasado a través de dicho medio de transmisión (también llamado canal de comunicación) variará aleatoriamente o se desvanecerá de acuerdo con una distribución de Rayleigh: el componente radial de la suma de dos Variables aleatorias gaussianas.

El desvanecimiento de Rayleigh se considera un modelo razonable para la propagación de señales troposféricas e ionosféricas, así como para el efecto de los entornos urbanos muy urbanizados en las señales de radio. El desvanecimiento de Rayleigh es más aplicable cuando no hay una propagación dominante a lo largo de una línea de visión entre el transmisor y el receptor. Si hay una línea de visión dominante, el desvanecimiento de Rician puede ser más aplicable. El desvanecimiento de Rayleigh es un caso especial de desvanecimiento de dos ondas con potencia difusa (TWDP).

La modelo

El desvanecimiento de Rayleigh es un modelo razonable cuando hay muchos objetos en el entorno que dispersan la señal de radio antes de que llegue al receptor. El teorema del límite central sostiene que, si hay suficiente dispersión, la respuesta de impulso del canal estará bien modelada como un proceso gaussiano independientemente de la distribución de los componentes individuales. Si no hay un componente dominante en la dispersión, dicho proceso tendrá una media cero y una fase distribuida uniformemente entre 0 y 2π radianes. Por lo tanto, la envolvente de la respuesta del canal tendrá una distribución de Rayleigh.

Llamando a esta variable aleatoria ${displaystyle R.$, tendrá una función de densidad de probabilidad:

${displaystyle p_{R}(r)={frac {2r} {Omega}e^{-r^{2}/Omega }, rgeq 0}$

Donde ${displaystyle Omega = 'operatorname {E} (R^{2})}$.

A menudo, los elementos de ganancia y fase de la distorsión de un canal se representan convenientemente como un número complejo. En este caso, el desvanecimiento de Rayleigh se presenta mediante la suposición de que las partes real e imaginaria de la respuesta se modelan mediante procesos gaussianos de media cero independientes e idénticamente distribuidos, de modo que la amplitud de la respuesta es la suma de dos de estos procesos.

Aplicabilidad

Densely built Manhattan has been shown to approach a Rayleigh-fading environment.

Un segundo de Rayleigh se desvanece con un máximo Doppler de 10 Hz.

Un segundo de Rayleigh se desvanece con un máximo Doppler de 100 Hz.

El requisito de que haya muchos dispersores presentes significa que el desvanecimiento de Rayleigh puede ser un modelo útil en los centros urbanos muy urbanizados donde no hay línea de visión entre el transmisor y el receptor y muchos edificios y otros objetos atenúan, reflejan, refractan y difractar la señal. El trabajo experimental en Manhattan ha encontrado un desvanecimiento cercano a Rayleigh allí. En la propagación de señales troposféricas e ionosféricas, muchas partículas en las capas atmosféricas actúan como dispersores y este tipo de entorno también puede aproximarse al desvanecimiento de Rayleigh. Si el entorno es tal que, además de la dispersión, se ve una señal fuertemente dominante en el receptor, generalmente causada por una línea de visión, entonces la media del proceso aleatorio ya no será cero, sino que variará alrededor de la potencia. -nivel del camino dominante. Tal situación puede modelarse mejor como el desvanecimiento de Rician.

Tenga en cuenta que el desvanecimiento de Rayleigh es un efecto a pequeña escala. Habrá propiedades generales del entorno, como la pérdida de trayectoria y el sombreado, sobre las que se superpone el desvanecimiento.

La rapidez con la que se desvanece el canal se verá afectada por la rapidez con la que se mueven el receptor y/o el transmisor. El movimiento provoca un desplazamiento Doppler en los componentes de la señal recibida. Las figuras muestran la variación de potencia durante 1 segundo de una señal constante después de pasar por un canal de desvanecimiento Rayleigh de un solo camino con un desplazamiento Doppler máximo de 10 Hz y 100 Hz. Estos desplazamientos Doppler corresponden a velocidades de aproximadamente 6 km/h (4 mph) y 60 km/h (40 mph) respectivamente a 1800 MHz, una de las frecuencias operativas para teléfonos móviles GSM. Esta es la forma clásica del desvanecimiento de Rayleigh. Tenga en cuenta en particular los 'desvanecimientos profundos' donde la fuerza de la señal puede caer por un factor de varios miles, o 30-40 dB.

Propiedades

Dado que se basa en una distribución bien estudiada con propiedades especiales, la distribución de Rayleigh se presta al análisis y las características clave que afectan el rendimiento de una red inalámbrica tienen expresiones analíticas.

Tenga en cuenta que los parámetros discutidos aquí son para un canal no estático. Si un canal no cambia con el tiempo, no se desvanece y, en cambio, permanece en un nivel particular. Las instancias separadas del canal en este caso no estarán correlacionadas entre sí, debido a la suposición de que cada uno de los componentes dispersos se desvanece de forma independiente. Una vez que se introduce un movimiento relativo entre cualquiera de los transmisores, receptores y dispersores, el desvanecimiento se correlaciona y varía en el tiempo.

Tasa de paso a nivel

La tasa de paso a nivel es una medida de la rapidez del desvanecimiento. Cuantifica la frecuencia con la que el desvanecimiento cruza algún umbral, generalmente en la dirección positiva. Para el desvanecimiento de Rayleigh, la tasa de paso a nivel es:

${displaystyle mathrm {LCR} ={sqrt {2pi} }f_{d}rho e^{-rho ^{2}$

Donde ${displaystyle f_{d}$ es el máximo Cambio Doppler y ${displaystyle ,!$ es el nivel de umbral normalizado al nivel de señal cuadrado (RMS):

${displaystyle rho ={frac {R_{mathrm {threshold} }{R_{mathrm {rms} }}}$

Duración media del desvanecimiento

La duración promedio de la desvanecimiento cuantifica cuánto tiempo pasa la señal por debajo del umbral ${displaystyle ,!$. Para Rayleigh, la duración promedio de la moda es:

${displaystyle mathrm {AFD} ={frac {f} ¿Qué? {2pi}}}}}$

La tasa de cruce a nivel y la duración promedio del desvanecimiento en conjunto brindan un medio útil para caracterizar la gravedad del desvanecimiento a lo largo del tiempo.

Para un valor umbral normalizado particular ${displaystyle rho }$, el producto de la duración promedio de la desvanecimiento y la tasa de cruce de nivel es una constante y se da por

${displaystyle mathrm {AFD} times mathrm {LCR} =1-e^{-rho ^{2}}.}$

Densidad espectral de potencia Doppler

El espectro de potencia Doppler normalizado de Rayleigh desvaneciendo con un máximo Doppler de 10 Hz.

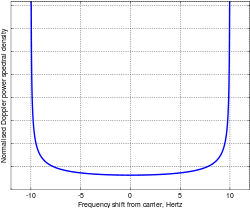
La densidad espectral de potencia Doppler de un canal que se desvanece describe cuánto ensanchamiento espectral provoca. Esto muestra cómo una frecuencia pura, por ejemplo, una sinusoide pura, que es un impulso en el dominio de la frecuencia, se propaga a través de la frecuencia cuando pasa por el canal. Es la transformada de Fourier de la función de autocorrelación temporal. Para el desvanecimiento de Rayleigh con una antena receptora vertical con igual sensibilidad en todas las direcciones, se ha demostrado que esto es:

${displaystyle S(nu)={frac {1}{pi F_{d}{sqrt {1-left({frac {nu {f}}} {f}}}}}} {f}}} {f}}} {f}}} {f}}} {f}}}}}} {f}}}} {f}}}} {f}}}}}}} {f}} {f}}}}} {f}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Donde ${displaystyle ,!$ es el cambio de frecuencia relativo a la frecuencia del portador. Esta ecuación es válida sólo para valores ${displaystyle ,!$ entre ${displaystyle pm f_{d}$; el espectro es cero fuera de este rango. Este espectro se muestra en la figura para un cambio máximo de Doppler de 10 Hz. La 'forma del arco' o 'forma del bebé' es la forma clásica de este espectro Doppler.

Generando el desvanecimiento de Rayleigh

Como se describió anteriormente, un canal de desvanecimiento de Rayleigh se puede modelar generando las partes real e imaginaria de un número complejo de acuerdo con variables gaussianas normales independientes. Sin embargo, a veces sucede que son simplemente las fluctuaciones de amplitud las que son de interés (como en la figura que se muestra arriba). Hay dos enfoques principales para esto. En ambos casos, el objetivo es producir una señal que tenga el espectro de potencia Doppler indicado anteriormente y las propiedades de autocorrelación equivalentes.

Modelo de Jake

En su libro, Jakes popularizó un modelo para el desvanecimiento de Rayleigh basado en sumar sinusoides. Deje que los dispersadores se distribuyan uniformemente alrededor de un círculo en ángulos ${displaystyle alpha _{n}$ con ${displaystyle k}$ Rayos emergentes de cada scatter. El turno de Doppler en Ray ${displaystyle n}$ es

${displaystyle ,!f_{n}=f_{d}cos alpha _{n}$

y, con ${displaystyle M}$ tales dispersadores, el Rayleigh desvaneciendo el ${displaystyle k^{text{th}}}$ onda con el tiempo ${displaystyle t}$ se puede modelar como:

${displaystyle {begin{aligned}R(t,k)=2{sqrt {2}left[sum] {fn} {fn}fnfn}fnfn}nsn}nn}n}n}n}nn}nnnn}nnnnnnnnnnnnnnnnnnnnnnnnnnMinnn}nnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn$

Aquí, ${displaystyle ,!alpha }$ y el ${displaystyle ,!beta _{n}$ y ${displaystyle ,!theta _{n,k}$ son parámetros modelo con ${displaystyle ,!alpha }$ normalmente se establece a cero, ${displaystyle ,!beta _{n}$ elegido para que no haya una cruza-correlación entre las partes reales e imaginarias de ${displaystyle R(t)}$:

${displaystyle ,!beta _{n}={frac ♪ No.$

y ${displaystyle ,!theta _{n,k}$ usada para generar múltiples ondas. Si un canal único está siendo modelado, por lo que sólo hay una forma de onda entonces ${displaystyle ,!theta _{n}$ puede ser cero. Si se está modelando un canal multipático y selectivo de frecuencias para que se necesitan múltiples formas de onda, Jakes sugiere que las formas de onda no correlativas son dadas por

${displaystyle theta # {n,k}=beta ¿Por qué?$

De hecho, se ha demostrado que las formas de onda están correlacionadas entre sí (tienen una correlación cruzada distinta de cero) excepto en circunstancias especiales. El modelo también es determinista (no tiene ningún elemento aleatorio una vez que se eligen los parámetros). Un modelo de Jakes modificado elige espaciados ligeramente diferentes para los dispersores y escala sus formas de onda utilizando secuencias de Walsh-Hadamard para garantizar una correlación cruzada cero. Configuración

${displaystyle alpha {fn} {fn} {fn0} {fn0} {fn}}}beta ¿Qué?.$

resulta en el siguiente modelo, generalmente denominado modelo Dent o modelo Jakes modificado:

${fn}sigualdad R(t,k)={sqrt {2}}sum _{n=1}{M}A_{k}(n)left(cos beta _{n}+jsin beta _{n}right)cos left(2pi f_{d}tcos+alpha _{n} }$

Funciones de ponderación ${displaystyle A_{k}(n)}$ son ${displaystyle k}$^T Walsh-Hadamard secuencia en ${displaystyle n}$. Dado que estos tienen cero lacorrelación cruzada por el diseño, este modelo resulta en formas de onda no correlativas. Las fases ${displaystyle ,!theta _{n}$ puede ser inicializado aleatoriamente y no tienen ningún efecto en las propiedades de correlación. La rápida transformación Walsh se puede utilizar para generar muestras de manera eficiente utilizando este modelo.

El modelo de Jakes también popularizó el espectro Doppler asociado con el desvanecimiento de Rayleigh y, como resultado, este espectro Doppler a menudo se denomina espectro de Jakes.

Ruido blanco filtrado

Otra forma de generar una señal con el espectro de potencia Doppler requerido es pasar una señal de ruido gaussiano blanco a través de un filtro gaussiano con una respuesta de frecuencia igual a la raíz cuadrada del espectro Doppler requerido. Aunque es más simple que los modelos anteriores y no determinista, presenta algunas cuestiones de implementación relacionadas con la necesidad de filtros de alto orden para aproximar la función de raíz cuadrada irracional en la respuesta y el muestreo de la forma de onda gaussiana a una velocidad adecuada.

Filtro Butterworth como densidad espectral de potencia Doppler

Filtrado por filtro Butterworth Serie de tiempo Rayleigh (frecuencia de muestreo es 120 Hz)

Según Doppler, PSD también se puede modelar a través del filtro Butterworth como:

${displaystyle S_{Doppler}(f)= habitH_{Butterworth} {B}{2k}}}}$

Donde f es una frecuencia, ${displaystyle H_{Butterworth}$ es la respuesta del filtro Butterworth, B es la constante de normalización, k es el orden del filtro y ${displaystyle f_{0}$ es la frecuencia de corte que debe seleccionarse con respecto al máximo turno de Doppler.