Desintegración radioactiva
Desintegración radiactiva (también conocida como desintegración nuclear, radiactividad, desintegración radiactiva o nuclear desintegración) es el proceso por el cual un núcleo atómico inestable pierde energía por radiación. Un material que contiene núcleos inestables se considera radioactivo. Tres de los tipos más comunes de desintegración son la desintegración alfa, beta y gamma, todas las cuales implican la emisión de partículas. La fuerza débil es el mecanismo responsable de la desintegración beta, mientras que los otros dos se rigen por el electromagnetismo y la fuerza nuclear.
La desintegración radiactiva es un proceso estocástico (es decir, aleatorio) a nivel de átomos individuales. De acuerdo con la teoría cuántica, es imposible predecir cuándo se desintegrará un átomo en particular, independientemente de cuánto tiempo haya existido el átomo. Sin embargo, para un número significativo de átomos idénticos, la tasa de desintegración general puede expresarse como una constante de desintegración o como vida media. Las vidas medias de los átomos radiactivos tienen un rango enorme; desde casi instantáneo hasta mucho más largo que la edad del universo.
El núcleo en descomposición se denomina radionúclido padre (o radioisótopo padre) y el proceso produce al menos un nucleido hijo. Excepto por la desintegración gamma o la conversión interna de un estado nuclear excitado, la desintegración es una transmutación nuclear que da como resultado una hija que contiene un número diferente de protones o neutrones (o ambos). Cuando cambia el número de protones, se crea un átomo de un elemento químico diferente.
Hay 28 elementos químicos naturales en la Tierra que son radiactivos y consisten en 34 radionucleidos (6 elementos tienen 2 radionucleidos diferentes) que datan de antes del tiempo de formación del Sistema Solar. Estos 34 se conocen como nucleidos primordiales. Ejemplos bien conocidos son el uranio y el torio, pero también se incluyen radioisótopos naturales de vida prolongada, como el potasio-40.
Historia del descubrimiento
La radiactividad fue descubierta en 1896 por los científicos Henri Becquerel y Marie Skłodowska-Curie, mientras trabajaban con materiales fosforescentes. Estos materiales brillan en la oscuridad después de la exposición a la luz, y Becquerel sospechaba que el brillo producido en los tubos de rayos cátodos por radiografías podría estar asociado con fosforescencia. Envolvió una placa fotográfica en papel negro y colocó varias sales fosforescentes. Todos los resultados fueron negativos hasta que usó sales de uranio. Las sales de uranio causaron un ennegrecimiento de la placa a pesar de que el plato se envolvió en papel negro. Estas radiaciones recibieron el nombre " Becquerel Rays ".
Pronto quedó claro que el ennegrecimiento de la placa no tenía nada que ver con la fosforescencia, ya que el ennegrecimiento también fue producido por sales no fosforescentes de uranio y por uranio metálico. A partir de estos experimentos, quedó claro que había una forma de radiación invisible que podía pasar a través del papel y estaba causando que la placa reaccionara como si estuviera expuesta a la luz.
Al principio, parecía que la nueva radiación era similar a las radiografías recientemente descubiertas. La investigación adicional de Becquerel, Ernest Rutherford, Paul Villard, Pierre Curie, Marie Curie y otros mostraron que esta forma de radiactividad fue significativamente más complicada. Rutherford fue el primero en darse cuenta de que todos esos elementos decaen de acuerdo con la misma fórmula exponencial matemática. Rutherford y su estudiante Frederick Soddy fueron los primeros en darse cuenta de que muchos procesos de descomposición dieron como resultado la transmutación de un elemento a otro. Posteriormente, la ley de desplazamiento radiactivo de los fajanos y Soddy se formuló para describir los productos de la descomposición alfa y beta.
Los primeros investigadores también descubrieron que muchos otros elementos químicos, además del uranio, tienen isótopos radiactivos. Una búsqueda sistemática de la radiactividad total en los minerales de uranio también guió a Pierre y Marie Curie para aislar dos nuevos elementos: polonio y radio. A excepción de la radiactividad del radio, la similitud química del radio al bario dificultó estos dos elementos.
El estudio de la radiactividad deMarie y Pierre Curie es un factor importante en la ciencia y la medicina. Después de que su investigación sobre los rayos de Becquerel los llevó al descubrimiento de radio y polonio, acuñaron el término " Radioactividad " Para definir la emisión de radiación ionizante por algunos elementos pesados. (Más tarde, el término se generalizó a todos los elementos). Su investigación sobre los rayos penetrantes en el uranio y el descubrimiento de radio lanzó una era de uso de radio para el tratamiento del cáncer. Su exploración del radio podría verse como el primer uso pacífico de la energía nuclear y el comienzo de la medicina nuclear moderna.
Peligros de salud tempranos

Los peligros de la radiación ionizante debido a la radiactividad y los rayos X no se reconocieron de inmediato.
Radiografías
El descubrimiento de los rayos X por parte de Wilhelm Röntgen en 1895 dio lugar a una amplia experimentación por parte de científicos, médicos e inventores. Muchas personas comenzaron a contar historias de quemaduras, pérdida de cabello y cosas peores en revistas técnicas ya en 1896. En febrero de ese año, el profesor Daniel y el Dr. Dudley de la Universidad de Vanderbilt realizaron un experimento que involucraba la radiografía de la cabeza de Dudley que resultó en su caída del cabello. Un informe del Dr. H.D. Hawks, que sufrió graves quemaduras en la mano y el pecho en una demostración de rayos X, fue el primero de muchos otros informes en Electrical Review.
Otros experimentadores, incluidos Elihu Thomson y Nikola Tesla, también informaron quemaduras. Thomson expuso deliberadamente un dedo a un tubo de rayos X durante un período de tiempo y sufrió dolor, hinchazón y ampollas. Otros efectos, incluidos los rayos ultravioleta y el ozono, a veces fueron culpados por el daño, y muchos médicos aún afirmaban que no había ningún efecto por la exposición a los rayos X.
A pesar de esto, hubo algunas primeras investigaciones sistemáticas sobre peligros y, ya en 1902, William Herbert Rollins escribió casi con desesperación que sus advertencias sobre los peligros que implicaba el uso descuidado de los rayos X no estaban siendo atendidas, ni por la industria ni por la industria. sus colegas. En ese momento, Rollins había demostrado que los rayos X podían matar a los animales de experimentación, podían provocar el aborto de una cobaya preñada y que podían matar a un feto. También destacó que "los animales varían en susceptibilidad a la acción externa de la luz X" y advirtió que estas diferencias deben tenerse en cuenta cuando los pacientes son tratados mediante radiografías.
Sustancias radiactivas
Sin embargo, los efectos biológicos de la radiación debida a sustancias radiactivas eran menos fáciles de medir. Esto brindó la oportunidad a muchos médicos y corporaciones de comercializar sustancias radiactivas como medicamentos patentados. Algunos ejemplos fueron los tratamientos con enemas de radio y las aguas que contienen radio para beber como tónicos. Marie Curie protestó contra este tipo de tratamiento y advirtió que "el radio es peligroso en manos inexpertas". Curie murió más tarde de anemia aplásica, probablemente causada por la exposición a la radiación ionizante. En la década de 1930, después de una serie de casos de necrosis ósea y muerte de entusiastas del tratamiento con radio, los medicamentos que contenían radio se habían retirado en gran medida del mercado (charlatanería radiactiva).
Protección contra la radiación
Solo un año después del descubrimiento de los rayos X por parte de Röntgen, el ingeniero estadounidense Wolfram Fuchs (1896) dio lo que probablemente sea el primer consejo de protección, pero no fue hasta 1925 que se celebró el primer Congreso Internacional de Radiología (ICR). se llevó a cabo y consideró establecer estándares internacionales de protección. Los efectos de la radiación sobre los genes, incluido el efecto del riesgo de cáncer, se reconocieron mucho más tarde. En 1927, Hermann Joseph Muller publicó una investigación que mostraba los efectos genéticos y, en 1946, recibió el Premio Nobel de Fisiología o Medicina por sus hallazgos.
El segundo ICR se llevó a cabo en Estocolmo en 1928 y propuso la adopción de la unidad röntgen, y se formó el Comité Internacional de Protección de Radio y Rayos X (IXRPC). Rolf Sievert fue nombrado presidente, pero una fuerza impulsora fue George Kaye del Laboratorio Nacional de Física Británico. El comité se reunió en 1931, 1934 y 1937.
Después de la Segunda Guerra Mundial, el aumento en el alcance y la cantidad de sustancias radiactivas que se manejaban como resultado de los programas nucleares militares y civiles llevó a que grandes grupos de trabajadores ocupacionales y el público estuvieran potencialmente expuestos a niveles nocivos de radiación ionizante. Esto se consideró en la primera ICR de posguerra convocada en Londres en 1950, cuando nació la actual Comisión Internacional de Protección Radiológica (ICRP). Desde entonces, la ICRP ha desarrollado el actual sistema internacional de protección radiológica, que cubre todos los aspectos de los peligros de la radiación.
En 2020, Hauptmann y otros 15 investigadores internacionales de ocho países, entre los que se encuentran: Institutos de Bioestadística, Investigación de Registro, Centros de Epidemiología del Cáncer, Epidemiología de la Radiación y luego también el Instituto Nacional del Cáncer (NCI) de EE. UU., la Agencia Internacional para la Investigación de Cancer (IARC) and Radiation Effects Research Foundation of Hiroshima estudiaron definitivamente a través de un metanálisis el daño resultante de las "dosis bajas" que han aquejado a las poblaciones de sobrevivientes de los bombardeos atómicos de Hiroshima y Nagasaki y también en numerosos accidentes de centrales nucleares ocurridos en el mundo. Estos científicos informaron, en JNCI Monographs: Epidemiological Studies of Low Dose Ionizing Radiation and Cancer Risk, que los nuevos estudios epidemiológicos respaldan directamente el exceso de riesgo de cáncer debido a las bajas dosis de radiación ionizante. En 2021, el investigador italiano Venturi informó las primeras correlaciones entre el radiocesio y el cáncer de páncreas con el papel del cesio en la biología y en la pancreatitis y la diabetes de origen pancreático.
Unidades
La unidad de actividad radiactiva del Sistema Internacional de Unidades (SI) es el Becquerel (BQ), nombrado en honor del científico Henri Becquerel. Un BQ se define como una transformación (o descomposición o desintegración) por segundo.
Una unidad más antigua de radiactividad es la curie, CI, que originalmente se definió como " la cantidad o masa de emanación de radio en equilibrio con un gramo de radio (elemento) ". Hoy, la curie se define como 3.7 × 10 10 desintegraciones por segundo, de modo que 1 curie (ci) = 3.7 × 10 10 bq . Para fines de protección radiológica, aunque la Comisión Reguladora Nuclear de los Estados Unidos permite el uso de la Unidad Curie junto con las unidades SI, las unidades de medición de la Unión Europea requerían que su uso para " Public Health... Propósitos " ser eliminado para el 31 de diciembre de 1985.
Los efectos de la radiación ionizante a menudo se miden en unidades de gris para mecánicos o sievert por daño al tejido.
tipos
La descomposición radiactiva da como resultado una reducción de la masa de descanso sumada, una vez que la energía liberada (la energía de desintegración ) ha escapado de alguna manera. Aunque la energía de descomposición a veces se define como asociada con la diferencia entre la masa de los productos nucleidos parentales y la masa de los productos de descomposición, esto es cierto solo de las mediciones de masa de descanso, donde se ha eliminado cierta energía del sistema de productos. Esto es cierto porque la energía de descomposición siempre debe llevar masa con ella, donde sea que aparezca (ver masa en relatividad especial) de acuerdo con la fórmula E = MC2. La energía de descomposición se libera inicialmente como la energía de los fotones emitidos más la energía cinética de las partículas emitidas masivas (es decir, partículas que tienen masa de descanso). Si estas partículas llegan al equilibrio térmico con su entorno y los fotones se absorben, entonces la energía de descomposición se transforma en energía térmica, que conserva su masa.
La energía de descomposición, por lo tanto, permanece asociada con una cierta medida de la masa del sistema de descomposición, llamada masa invariante, que no cambia durante la descomposición, a pesar de que la energía de la descomposición se distribuye entre las partículas de descomposición. La energía de los fotones, la energía cinética de las partículas emitidas y, más tarde, la energía térmica de la materia circundante, todos contribuyen a la masa invariante del sistema. Por lo tanto, si bien la suma de las masas de descanso de las partículas no se conserva en la desintegración radiactiva, la masa del sistema y la masa invariante del sistema (y también la energía total del sistema) se conserva en cualquier proceso de desintegración. Esta es una reexpresión de las leyes equivalentes de conservación de la energía y la conservación de la masa.
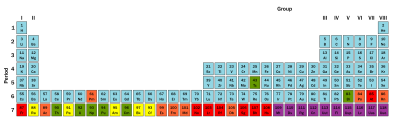
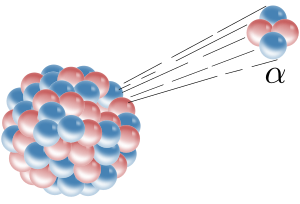
Alpha, beta y gamma Decay
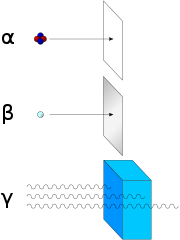
Los primeros investigadores descubrieron que un campo eléctrico o magnético podía dividir las emisiones radiactivas en tres tipos de haces. Los rayos recibieron los nombres alfa, beta y gamma, en orden creciente de su capacidad para penetrar la materia. La descomposición alfa se observa solo en elementos más pesados de número atómico 52 (telurio) y mayores, con la excepción del berilio-8 (que se desintegra en dos partículas alfa). Los otros dos tipos de descomposición se observan en todos los elementos. El plomo, número atómico 82, es el elemento más pesado que tiene isótopos estables (hasta el límite de medición) a la descomposición radiactiva. La descomposición radiactiva se observa en todos los isótopos de todos los elementos de número atómico 83 (bismuto) o mayor. El bismuto-209, sin embargo, es muy poco radiactivo, con una vida media mayor que la edad del universo; los radioisótopos con vidas medias extremadamente largas se consideran efectivamente estables a efectos prácticos.
Al analizar la naturaleza de los productos de desintegración, era obvio por la dirección de las fuerzas electromagnéticas aplicadas a las radiaciones por campos eléctricos y magnéticos externos que las partículas alfa tenían una carga positiva, las partículas beta tenían una carga negativa y los rayos gamma eran neutrales. Por la magnitud de la desviación, estaba claro que las partículas alfa eran mucho más masivas que las partículas beta. Pasar partículas alfa a través de una ventana de vidrio muy delgada y atraparlas en un tubo de descarga permitió a los investigadores estudiar el espectro de emisión de las partículas capturadas y, en última instancia, demostró que las partículas alfa son núcleos de helio. Otros experimentos mostraron que la radiación beta, resultante de la descomposición y los rayos catódicos, eran electrones de alta velocidad. Asimismo, se descubrió que la radiación gamma y los rayos X son radiación electromagnética de alta energía.
También comenzó a examinarse la relación entre los tipos de desintegración: por ejemplo, casi siempre se encontró que la desintegración gamma estaba asociada con otros tipos de desintegración y ocurría aproximadamente al mismo tiempo o después. Se descubrió que la desintegración gamma como un fenómeno separado, con su propia vida media (ahora denominada transición isomérica), en la radiactividad natural es el resultado de la desintegración gamma de los isómeros nucleares metaestables excitados, que a su vez se crearon a partir de otros tipos de desintegración. Aunque las radiaciones alfa, beta y gamma se encontraron con mayor frecuencia, finalmente se descubrieron otros tipos de emisión. Poco después del descubrimiento del positrón en los productos de rayos cósmicos, se descubrió que el mismo proceso que opera en la desintegración beta clásica también puede producir positrones (emisión de positrones), junto con neutrinos (la desintegración beta clásica produce antineutrinos).
Captura de electrones
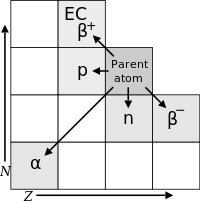
En la captura de electrones, se descubrió que algunos nucleidos ricos en protones capturan sus propios electrones atómicos en lugar de emitir positrones y, posteriormente, estos nucleidos emiten solo un neutrino y un rayo gamma desde el núcleo excitado (y a menudo también electrones Auger y característicos). rayos X, como resultado de la reordenación de electrones para ocupar el lugar del electrón capturado faltante). Estos tipos de desintegración implican la captura nuclear de electrones o la emisión de electrones o positrones y, por lo tanto, actúa para mover un núcleo hacia la proporción de neutrones a protones que tiene la menor energía para un número total dado de nucleones. En consecuencia, esto produce un núcleo más estable (de menor energía).
Un proceso hipotético de captura de positrones, análogo a la captura de electrones, es teóricamente posible en los átomos de antimateria, pero no se ha observado, ya que los átomos de antimateria complejos más allá del antihelio no están disponibles experimentalmente. Tal descomposición requeriría átomos de antimateria al menos tan complejos como el berilio-7, que es el isótopo más ligero conocido de la materia normal para sufrir la descomposición por captura de electrones.
Emisión de nucleones
Poco después del descubrimiento del neutrón en 1932, Enrico Fermi se dio cuenta de que ciertas reacciones raras de desintegración beta producen inmediatamente neutrones como una partícula de desintegración adicional, lo que se conoce como emisión de neutrones beta retardada. La emisión de neutrones suele ocurrir a partir de núcleos que se encuentran en un estado excitado, como el 17O* excitado producido por la desintegración beta de 17N. El proceso de emisión de neutrones en sí está controlado por la fuerza nuclear y, por lo tanto, es extremadamente rápido, a veces denominado "casi instantáneo". Eventualmente se observó emisión aislada de protones en algunos elementos. También se encontró que algunos elementos pesados pueden sufrir una fisión espontánea en productos que varían en composición. En un fenómeno llamado decaimiento de cúmulos, se descubrió que los átomos emitían espontáneamente combinaciones específicas de neutrones y protones distintas de las partículas alfa (núcleos de helio).
Tipos de caries más exóticos
Se descubrió que otros tipos de desintegración radiactiva emiten partículas vistas anteriormente, pero a través de mecanismos diferentes. Un ejemplo es la conversión interna, que da como resultado una emisión inicial de electrones, y luego, a menudo, más rayos X característicos y emisiones de electrones Auger, aunque el proceso de conversión interna no implica desintegración beta ni gamma. No se emite un neutrino, y ninguno de los electrones y fotones emitidos se origina en el núcleo, aunque la energía para emitirlos todos se origina allí. El decaimiento de conversión interna, como el decaimiento gamma de transición isomérica y la emisión de neutrones, implica la liberación de energía por parte de un nucleido excitado, sin la transmutación de un elemento en otro.
Se conocen eventos raros que implican una combinación de dos eventos de tipo de desintegración beta que ocurren simultáneamente (ver más abajo). Se permite que ocurra cualquier proceso de descomposición que no viole las leyes de conservación de la energía o del momento (y quizás otras leyes de conservación de partículas), aunque no todos han sido detectados. Un ejemplo interesante discutido en una sección final, es la desintegración beta del estado ligado del renio-187. En este proceso, la desintegración de electrones beta del nucleido original no va acompañada de la emisión de electrones beta, porque la partícula beta ha sido capturada en la capa K del átomo emisor. Se emite un antineutrino, como en todas las desintegraciones beta negativas.
Si las circunstancias energéticas son favorables, un radionúclido dado puede sufrir muchos tipos de desintegración en competencia, con algunos átomos desintegrándose por una vía y otros desintegrándose por otra. Un ejemplo es el cobre-64, que tiene 29 protones y 35 neutrones, que se desintegra con una vida media de 12,7004 (13) horas. Este isótopo tiene un protón desapareado y un neutrón desapareado, por lo que el protón o el neutrón pueden decaer en la otra partícula, que tiene un isospín opuesto. Es más probable que este nucleido en particular (aunque no todos los nucleidos en esta situación) se desintegre a través de beta más decaimiento (61.52(26)%) que a través de la captura de electrones (38,48(26)%). Los estados de energía excitados resultantes de estas desintegraciones que no terminan en un estado de energía fundamental, también producen conversión interna posterior y desintegración gamma en casi el 0,5% del tiempo.
Lista de modos de caída
| Modo | Nombre | Medida | Cambios en el cuello |
|---|---|---|---|
| emisión alfa | Una partícula alfa ()A = 4, Z = 2) emitido por el núcleo | ()A − 4, Z − 2) |
| emisión de protones | Un protón expulsado del núcleo | ()A, 1, Z −1) |
| 2-proton emission | Dos protones expulsados del núcleo simultáneamente | ()A, 2, Z − 2) |
| emisión de neutrones | Un neutrón expulsado del núcleo | ()A, 1, Z) |
| 2-neutron emission | Dos neutrones expulsados del núcleo simultáneamente | ()A, 2, Z) |
| captación de electrones | Un núcleo captura un electrón orbitante y emite un neutrino; el núcleo hija se deja en un estado inestable excitado | ()A, Z −1) |
| emisión de positrones | Un protón nuclear se convierte en un neutrón emitiendo un positrón y un neutrino electron | ()A, Z −1) |
| emisión de positrones | En NUBASE2020, ß+ se refiere a combinados tasa de captura de electrones (ε) y emisión de positrones (e+): ß+ = ε + e+ | ()A, Z −1) |
| β - decaimiento | Un núcleo emite un electrón y un electron antineutrino | ()A, Z + 1) |
| doble β decaimiento | Un núcleo emite dos electrones y dos antineutrinos | ()A, Z + 2) |
| doble β decaimiento | Un núcleo emite dos positrones y dos neutrinos | ()A, Z − 2) |
| Emisión de neutrones retardada | Un núcleo decae por β− emisión a un estado excitado, que luego emite un neutron | ()A, 1, Z + 1) |
| β−- Emisión tardía de 2 neutrones | Un núcleo decae por β− emisión a un estado excitado, que luego emite dos neutrones | ()A, 2, Z + 1) |
| β−- Emisión tardía de 3 neutrones | Un núcleo decae por β− emisión a un estado excitado, que luego emite tres neutrones | ()A 3 - 3 Z + 1) |
| β+- Emisión tardía de protones | Un núcleo decae por β+ emisión a un estado excitado, que luego emite un protón | ()A, 1, Z − 2) |
| β+- Emisión tardía de 2 protones | Un núcleo decae por β+ emisión a un estado excitado, que luego emite dos protones | ()A, 2, Z 3) - |
| β+- Emisión tardía de 3 protones | Un núcleo decae por β+ emisión a un estado excitado, que luego emite tres protones | ()A 3 - 3 Z − 4) |
| β−- Emisión tardía de alfa | Un núcleo decae por β− emisión a un estado excitado, que luego emite una partícula α | ()A − 4, Z −1) |
| β+- Emisión tardía de alfa | Un núcleo decae por β+ emisión a un estado excitado, que luego emite una partícula | ()A − 4, Z 3) - |
| β−- Emisión tardía de deuteronomio | Un núcleo decae por β− emisión a un estado excitado, que luego emite un deuterono | ()A, 2, Z) |
| β−- Emisión tardía de tritón | Un núcleo decae por β− emisión a un estado excitado, que luego emite un tritón | ()A 3 - 3 Z) |
| desintegración en racimo | Un núcleo emite un tipo específico de núcleo menor (A1, Z1) que es más grande que una partícula alfa | ()A − A1, Z −Z1) ()A1,Z1) |
| transición interna (isomeric) | Un núcleo en un estado metastable cae a un estado de energía inferior emitiendo un fotono o expulsando un electrón | ()A, Z) |
| fisión espontánea | Un núcleo se desintegra en dos o más núcleos más pequeños y otras partículas, todas las cuales pueden variar con cada decaimiento | variable |
| β+- fisión tardía | Un núcleo decae por β+ emisión a un estado excitado, que luego sufre fisión espontánea | β+ " variable |
| β−- fisión tardía | Un núcleo decae por β− emisión a un estado excitado, que luego sufre fisión espontánea | β− variable |
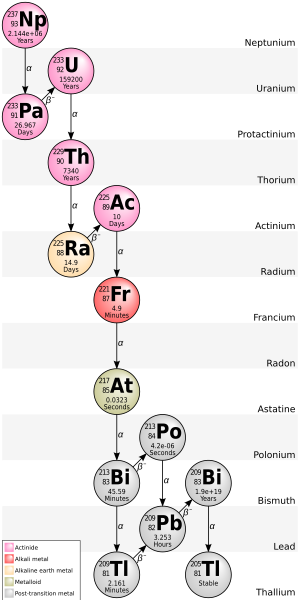
Cadenas de decaimiento y múltiples modos
El nucleido hijo de un evento de desintegración también puede ser inestable (radiactivo). En este caso, también se descompondrá, produciendo radiación. El segundo nucleido hijo resultante también puede ser radiactivo. Esto puede conducir a una secuencia de varios eventos de descomposición llamada cadena de descomposición (consulte este artículo para obtener detalles específicos de importantes cadenas de descomposición natural). Eventualmente, se produce un nucleido estable. Cualquier desintegración hija que sea el resultado de una desintegración alfa también dará como resultado la creación de átomos de helio.
Algunos radionúclidos pueden tener varios caminos diferentes de descomposición. Por ejemplo, 35.94(6)% del bismuto-212 se descompone, a través de la emisión alfa, en talio -208 while 64,06(6)% del bismuto-212 se descompone, a través de la emisión beta, en polonio -212. Tanto el talio-208 como el polonio-212 son productos secundarios radiactivos del bismuto-212 y ambos se descomponen directamente en plomo-208 estable.
Ocurrencia y aplicaciones
Según la teoría del Big Bang, los isótopos estables de los tres elementos más ligeros (H, He y rastros de Li) se produjeron muy poco después de la aparición del universo, en un proceso llamado nucleosíntesis del Big Bang. Estos nucleidos estables más livianos (incluido el deuterio) sobreviven hasta el día de hoy, pero cualquier isótopo radiactivo de los elementos livianos producidos en el Big Bang (como el tritio) se descompuso hace mucho tiempo. Los isótopos de elementos más pesados que el boro no se produjeron en absoluto en el Big Bang, y estos primeros cinco elementos no tienen radioisótopos de larga vida. Así, todos los núcleos radiactivos son, por lo tanto, relativamente jóvenes con respecto al nacimiento del universo, habiéndose formado más tarde en varios otros tipos de nucleosíntesis en estrellas (en particular, supernovas), y también durante interacciones en curso entre isótopos estables y partículas energéticas. Por ejemplo, el carbono 14, un nucleido radiactivo con una vida media de solo 5700(30) años, se produce constantemente en la atmósfera superior de la Tierra debido a las interacciones entre los rayos cósmicos y el nitrógeno.
Los nucleidos que se producen por desintegración radiactiva se denominan nucleidos radiogénicos, tanto si son estables como si no. Existen nucleidos radiogénicos estables que se formaron a partir de radionucleidos extintos de vida corta en el Sistema Solar primitivo. La presencia adicional de estos nucleidos radiogénicos estables (como el xenón-129 del extinto yodo-129) en el contexto de los nucleidos primordiales estables se puede inferir por varios medios.
La desintegración radiactiva se ha utilizado en la técnica de marcaje radioisotópico, que se utiliza para rastrear el paso de una sustancia química a través de un sistema complejo (como un organismo vivo). Una muestra de la sustancia se sintetiza con una alta concentración de átomos inestables. La presencia de la sustancia en una u otra parte del sistema se determina detectando las ubicaciones de los eventos de descomposición.
Bajo la premisa de que la desintegración radiactiva es realmente aleatoria (en lugar de simplemente caótica), se ha utilizado en generadores de números aleatorios de hardware. Debido a que no se cree que el proceso varíe significativamente en el mecanismo a lo largo del tiempo, también es una herramienta valiosa para estimar las edades absolutas de ciertos materiales. En el caso de los materiales geológicos, los radioisótopos y algunos de sus productos de desintegración quedan atrapados cuando una roca se solidifica y luego se pueden usar (sujeto a muchas calificaciones bien conocidas) para estimar la fecha de la solidificación. Estos incluyen la verificación de los resultados de varios procesos simultáneos y sus productos entre sí, dentro de la misma muestra. De manera similar, y también sujeto a calificación, se puede estimar la tasa de formación de carbono-14 en varias eras, la fecha de formación de materia orgánica dentro de un cierto período relacionado con la vida media del isótopo, porque el carbono-14 queda atrapado cuando la materia orgánica crece e incorpora el nuevo carbono-14 del aire. A partir de entonces, la cantidad de carbono-14 en la materia orgánica disminuye de acuerdo con los procesos de descomposición que también pueden verificarse de forma independiente por otros medios (como la verificación del carbono-14 en anillos de árboles individuales, por ejemplo).
Efecto Szilard-Chalmers
El efecto Szilard-Chalmers es la ruptura de un enlace químico como resultado de una energía cinética impartida por la descomposición radiactiva. Funciona mediante la absorción de neutrones por parte de un átomo y la posterior emisión de rayos gamma, a menudo con cantidades significativas de energía cinética. Esta energía cinética, según la tercera ley de Newton, hace retroceder al átomo en descomposición, lo que hace que se mueva con suficiente velocidad para romper un enlace químico. Este efecto se puede utilizar para separar isótopos por medios químicos.
El efecto Szilard-Chalmers fue descubierto en 1934 por Leó Szilárd y Thomas A. Chalmers. Observaron que después del bombardeo con neutrones, la ruptura de un enlace en el yoduro de etilo líquido permitía eliminar el yodo radiactivo.
Orígenes de los nucleidos radiactivos
Los nucleidos primordiales radiactivos que se encuentran en la Tierra son residuos de antiguas explosiones de supernovas que ocurrieron antes de la formación del Sistema Solar. Son la fracción de radionucleidos que sobrevivieron desde ese momento, a través de la formación de la nebulosa solar primordial, a través de la acreción de planetas, y hasta el presente. Los radionúclidos radiogénicos de vida corta que se encuentran naturalmente en las rocas actuales son hijas de esos núclidos primordiales radiactivos. Otra fuente menor de nucleidos radiactivos naturales son los nucleidos cosmogénicos, que se forman por el bombardeo de material con rayos cósmicos en la atmósfera o la corteza terrestre. La descomposición de los radionúclidos en las rocas del manto y la corteza terrestre contribuye significativamente al balance de calor interno de la Tierra.
Tarifas
La tasa de desintegración, o actividad, de una sustancia radiactiva se caracteriza por los siguientes parámetros independientes del tiempo:
- El semivida, t1/2, es el tiempo tomado para la actividad de una cantidad determinada de una sustancia radiactiva para decaer a la mitad de su valor inicial.
- El constante, λ "lambda", el recíproco de la vida media (en s−1), a veces referido como simplemente Tasa de desintegración.
- El vida, τ "tau", la vida media (1/e vida) de una partícula radiactiva antes de la decadencia.
Aunque son constantes, están asociadas con el comportamiento estadístico de las poblaciones de átomos. En consecuencia, las predicciones que utilizan estas constantes son menos precisas para muestras minúsculas de átomos.
En principio, una vida media, una tercera vida o incluso una vida (1/√2) pueden usarse exactamente de la misma manera que la vida media; pero la vida media y la vida media t1/2 se han adoptado como tiempos estándar asociados con el decaimiento exponencial.
Esos parámetros pueden estar relacionados con los siguientes parámetros dependientes del tiempo:
- Actividad total, A, es el número de decaimientos por unidad de tiempo de una muestra radiactiva.
- Número de partículas, N, es el número total de partículas en la muestra.
- Actividad específica, a, es el número de decaimientos por hora unidad por cantidad de sustancia de la muestra a tiempo establecido a cero (t = 0). " Cantidad de sustancia" puede ser la masa, volumen o topos de la muestra inicial.
Estos están relacionados de la siguiente manera:
- t1/2=In ()2)λ λ =τ τ In ()2)A=− − dNdt=λ λ N=In ()2)t1/2NSAa0=− − dNdtSilenciot=0=λ λ N0{displaystyle {begin{aligned}t_{1/2} limit={frac {ln(2)}{lambda }=tau ln(2)[2pt]A sensible=-{frac {mathrm {d} N={frac {ln(2)}N\[2pt]S_{A}a_{0} {fn} {fn} {fn} {fn} {fn} {fn} {fnfn}}}\\cH00}}\\cH00}\fn0}\fn}\\\\\\fn\\\cH0}\cH00}cH0}\cH00}cH00}cH00}cH00}\\cH00}\\\\\\\cH00}\\\cH00}\cH00}\cH00}\\cH00}cH00}\cH00}\cH00}\cH00}\\cH00}\cH00} {fnK} No. Silencio. No.
donde n 0 es la cantidad inicial de sustancia activa, sustancia que tiene el mismo porcentaje de partículas inestables que cuando se formó la sustancia.
Matemáticas
Law Universal
Las matemáticas de la desintegración radiactiva dependen de una suposición clave de que un núcleo de un radionucleido no tiene " memoria " o forma de traducir su historia en su comportamiento actual. Un núcleo no " edad " Con el pasar del tiempo. Por lo tanto, la probabilidad de su descomposición no aumenta con el tiempo, sino que permanece constante, sin importar cuánto tiempo haya existido el núcleo. Esta probabilidad constante puede diferir enormemente entre un tipo de núcleo y otro, lo que lleva a las diferentes tasas de descomposición observadas. Sin embargo, sea cual sea la probabilidad, no cambia con el tiempo. Esto está en marcado contraste con objetos complejos que muestran envejecimiento, como automóviles y humanos. Estos sistemas de envejecimiento tienen una posibilidad de descomposición por unidad de tiempo que aumenta desde el momento en que comienzan su existencia.
procesos agregados, como la descomposición radiactiva de un bulto de átomos, para los cuales la probabilidad de realización de un solo evento es muy pequeña, pero en la que el número de situaciones de tiempo es tan grande que existe una tasa de eventos razonable, están modelados por la distribución de Poisson, que es discreta. La desintegración radiactiva y las reacciones de partículas nucleares son dos ejemplos de dichos procesos agregados. Las matemáticas de los procesos de Poisson se reducen a la ley de la descomposición exponencial, que describe el comportamiento estadístico de un gran número de núcleos, en lugar de un núcleo individual. En el siguiente formalismo, el número de núcleos o la población de núcleos n , es, por supuesto, una variable discreta (un número natural), pero para cualquier muestra física n es tan grande es tan grande que puede tratarse como una variable continua. El cálculo diferencial se usa para modelar el comportamiento de la descomposición nuclear.
Proceso de una decena
Considere el caso de un nuclide a que decae en otro b < por algún proceso a → b (emisión de otras partículas, como neutrinos electrónicos
ν
e y electrones e - Como en la descomposición beta, son irrelevantes en lo que sigue). La descomposición de un núcleo inestable es completamente aleatorio en el tiempo, por lo que es imposible predecir cuándo decae un átomo particular. Sin embargo, es igualmente probable que se descomponga en cualquier instante en el tiempo. Por lo tanto, dada una muestra de un radioisótopo particular, el número de eventos de descomposición - d n se espera que ocurra en un pequeño intervalo de tiempo d t es proporcional al número de átomos presentes n , es decir
- − − dNdt∝ ∝ N{displaystyle -{frac {mathrm {d} {mathrm} t}propto N}
Los radionúclidos particulares se desintegran a diferentes velocidades, por lo que cada uno tiene su propia constante de desintegración λ. El decaimiento esperado −dN/N es proporcional a un incremento de tiempo, dt:
− − dNN=λ λ dt{displaystyle -{frac {mathrm} No.
El signo negativo indica que n disminuye a medida que aumenta el tiempo, a medida que los eventos de descomposición siguen uno tras otro. La solución a esta ecuación diferencial de primer orden es la función:
- N()t)=N0e− − λ λ t{displaystyle N(t)=N_{0},e^{-{lambda }t}
where n 0 es el valor de n en el tiempo t = 0, con la constante de descomposición expresada como λ
Tenemos para todos los tiempos t ::
- NA+NB=Ntotal=NA0,{displaystyle N_{A}+N_{B}=N_{text{total}=N_{A0}
donde Ntotal es el número constante de partículas a lo largo del proceso de descomposición, que es igual al número inicial de nucleidos A ya que esta es la sustancia inicial.
Si el número de núcleos A no decaídos es:
- NA=NA0e− − λ λ t{displaystyle No.
entonces el número de núcleos de B (es decir, el número de A núcleos) es
- NB=NA0− − NA=NA0− − NA0e− − λ λ t=NA0()1− − e− − λ λ t).{displaystyle No. t}=N_{A0}left(1-e^{-lambda t}right). }
El número de desintegraciones observadas en un intervalo dado obedece las estadísticas de Poisson. Si el número promedio de desacuerdos es ⟨ n ⟩ , la probabilidad de un número dado de desintegraciones n es
- P()N)=.. N.. Nexp ()− − .. N.. )N!.{displaystyle P(N)={frac ¡No!
Procesos de descomposición en cadena
Cadena de dos decaimientos
Ahora considere el caso de una cadena de dos desintegraciones: un nucleido A decayendo en otro B por un proceso, luego B decayendo en otro C por un segundo proceso, es decir, A → B → C. La ecuación anterior no se puede aplicar a la cadena de decaimiento, pero se puede generalizar de la siguiente manera. Dado que A se descompone en B, entonces B decae en C, la actividad de A se suma al número total de B nucleidos en la muestra actual, antes de que esos B nucleidos se descompongan y reduzcan el número de nucleidos que conducen a la muestra posterior. En otras palabras, el número de núcleos de segunda generación B aumenta como resultado de la descomposición de los núcleos de primera generación de A, y disminuye como resultado de su propia descomposición en los núcleos de tercera generación C. La suma de estos dos términos da la ley para una cadena de descomposición de dos nucleidos:
- dNBdt=− − λ λ BNB+λ λ ANA.{displaystyle {frac {mathrm} {fn} {fn} {fn} {f}}=lambda ################################################################################################################################################################################################################################################################ No.
La tasa de cambio de NB, es decir dNB/dt, está relacionado con los cambios en las cantidades de A y B, NB puede aumentar a medida que B se produce a partir de A y disminuye a medida que B produce C.
Reescribiendo usando los resultados anteriores:
dNBdt=− − λ λ BNB+λ λ ANA0e− − λ λ At{displaystyle {frac {mathrm} {fn} {fn} {fn} {f}}=lambda ################################################################################################################################################################################################################################################################ ¿Qué?
Los subíndices simplemente se refieren a los nucleidos respectivos, es decir, NA es el número de nucleidos de tipo A; NA0 es el número inicial de nucleidos de tipo A; λA es la constante de decaimiento de A – y de manera similar para el nucleido B. Resolviendo esta ecuación para NB da:
- NB=NA0λ λ Aλ λ B− − λ λ A()e− − λ λ At− − e− − λ λ Bt).{displaystyle N_{B}={frac {N_{A0}lambda ¿Qué? ¿Por qué? ¿Qué? - ¿Qué? - ¿Sí? }
en el caso donde b es un nucleido estable ( λ b = 0), esta ecuación se reduce a la solución anterior:
- limλ λ B→ → 0[NA0λ λ Aλ λ B− − λ λ A()e− − λ λ At− − e− − λ λ Bt)]=NA0λ λ A0− − λ λ A()e− − λ λ At− − 1)=NA0()1− − e− − λ λ At),{displaystyle lim _{lambda ¿Qué? {N_{A0}lambda ¿Qué? ¿Por qué? ¿Qué? - ¿Qué? ¿Por qué? {N_{A0}lambda ¿Qué? ¿Qué? ################################################################################################################################################################################################################################################################ - ¿Sí?
Como se muestra arriba para una decadencia. La solución se puede encontrar mediante el método del factor de integración, donde el factor de integración es e λ b t . Este caso es quizás el más útil, ya que puede derivar tanto la ecuación de una decaía (arriba) como la ecuación para las cadenas de múltiples decayas (a continuación) más directamente.
Cadena de cualquier número de desembolsos
Para el caso general de cualquier número de desintegraciones consecutivas en una cadena de descomposición, es decir, a 1 → a 2 ··· → A I ··· → a d , donde d es el número de desembolsos y i es un índice ficticio ( i = 1, 2, 3,... d ), cada población nuclida se puede encontrar en términos de la población anterior. En este caso n 2 = 0 , n 3 = 0 ,..., n d = 0 . Usando el resultado anterior en una forma recursiva:
- dNjdt=− − λ λ jNj+λ λ j− − 1N()j− − 1)0e− − λ λ j− − 1t.{displaystyle {frac {mathrm} No. ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ No.
La solución general al problema recursivo viene dada por las ecuaciones de Bateman:
ND=N1()0)λ λ D.. i=1Dλ λ icie− − λ λ itci=∏ ∏ j=1,iل ل jDλ λ jλ λ j− − λ λ i{displaystyle {begin{aligned}N_{D} {frac {N_{1}(0)}{lambda - Sí. ################################################################################################################################################################################################################################################################ ¿Por qué? - ¿Qué? _{j=1,ineq ## {fnMicroc {fnMicrosoft Sans Serif} ¿Qué? _{j}-lambda ¿Qué?
Modos alternativos
En todos los ejemplos anteriores, el nucleido inicial se descompone en un solo producto. Considere el caso de un nucleido inicial que puede decaer en cualquiera de los dos productos, es decir, A → B y A → C en paralelo. Por ejemplo, en una muestra de potasio-40, el 89,3 % de los núcleos se descomponen en calcio-40 y el 10,7 % en argón-40. Tenemos para todos los tiempos t:
- N=NA+NB+NC{displaystyle N=N_{A}+N_{B}+N_{C}
que es constante, ya que el número total de nucleidos permanece constante. Diferenciando con respecto al tiempo:
- dNAdt=− − ()dNBdt+dNCdt)− − λ λ NA=− − NA()λ λ B+λ λ C){displaystyle {begin{aligned}{frac {mathrm} ¿Qué? N_{A} Alguien=-N_{A}left(lambda) ################################################################################################################################################################################################################################################################ ¿Por qué?
definiendo la constante de decaimiento total λ en términos de la suma de constantes de decaimiento parcial λB y λC:
- λ λ =λ λ B+λ λ C.{displaystyle lambda =lambda _{B}+lambda _{C}
Resolviendo esta ecuación para NA:
- NA=NA0e− − λ λ t.{displaystyle N_{A}=N_{A0}e^{-lambda t}
donde NA0 es el número inicial de nucleido A. Al medir la producción de un nucleido, solo se puede observar la constante de descomposición total λ. Las constantes de decaimiento λB y λC determina la probabilidad de que la descomposición resulte en productos B o C de la siguiente manera:
- NB=λ λ Bλ λ NA0()1− − e− − λ λ t),{displaystyle N_{B}={frac {lambda ¿Qué? }N_{A0}left(1-e^{-lambda t}right),}
- NC=λ λ Cλ λ NA0()1− − e− − λ λ t).{displaystyle N_{C}={frac {fnMicrode ¿Qué? }N_{A0}left(1-e^{-lambda t}right). }
porque la fracción λB/λ de núcleos se descompone en B mientras que la fracción λC/λ de los núcleos se descomponen en C.
Corolarios de leyes
Las ecuaciones anteriores también se pueden escribir utilizando cantidades relacionadas con el número de partículas de nucleido N en una muestra;
- La actividad: A = λN.
- La cantidad de sustancia: n = N/NA.
- La masa: m = Mn = MN/NA.
donde NA = 6.02214076×1023 mol−1 es la constante de Avogadro, M es la masa molar de la sustancia en kg/mol, y la cantidad de la sustancia n está en moles.
Tiempo de decaimiento: definiciones y relaciones
Constante de tiempo y vida media
Para la solución de un decaimiento A → B:
- N=N0e− − λ λ t=N0e− − t/τ τ ,{displaystyle N=N_{0},e^{-{lambda ¡No!
la ecuación indica que la constante de decaimiento λ tiene unidades de t−1, y por lo tanto también puede representarse como 1/τ, donde τ es un tiempo característico del proceso llamado constante de tiempo.
En un proceso de desintegración radiactiva, esta constante de tiempo es también el tiempo de vida medio de los átomos en descomposición. Cada átomo "vive" durante una cantidad finita de tiempo antes de que decaiga, y se puede demostrar que este tiempo de vida medio es la media aritmética de todos los átomos' vidas, y que es τ, que nuevamente está relacionado con la constante de decaimiento de la siguiente manera:
- τ τ =1λ λ .{displaystyle tau ={frac {1}{lambda }}
Esta forma también es válida para procesos de dos decaimientos simultáneamente A → B + C, insertando los valores equivalentes de las constantes de decaimiento (como se indicó anteriormente)
- λ λ =λ λ B+λ λ C{displaystyle lambda =lambda _{B}+lambda ¿Qué?
en la solución de descomposición conduce a:
- 1τ τ =λ λ =λ λ B+λ λ C=1τ τ B+1τ τ C{displaystyle {frac {1}{tau }=lambda =lambda _{B}+lambda ¿Qué? {1}{tau ¿Qué?
Vida media
Un parámetro más utilizado es la vida media T1/2. Dada una muestra de un radionúclido en particular, la vida media es el tiempo que tardan en desintegrarse la mitad de los átomos del radionúclido. Para el caso de reacciones nucleares de un decaimiento:
- N=N0e− − λ λ t=N0e− − t/τ τ ,{displaystyle N=N_{0},e^{-{lambda ¡No!
la vida media está relacionada con la constante de descomposición de la siguiente manera: establece N = N0/2 y t = T1/2 para obtener
- t1/2=In 2λ λ =τ τ In 2.{displaystyle t_{1/2}={frac {fnMin} 2}{lambda }=tau ln 2.}
Esta relación entre la vida media y la constante de desintegración muestra que las sustancias altamente radiactivas se gastan rápidamente, mientras que las que radian débilmente duran más. La vida media de los radionucleidos conocidos varía en casi 54 órdenes de magnitud, desde más de 2,25(9)×1024 años (6.9×1031 seg) para el núclido casi estable 128Te, hasta 8.6(6)×10−23 segundos para el nucleido altamente inestable 5H.
El factor de ln(2) en las relaciones anteriores resulta del hecho de que el concepto de "vida media" es simplemente una forma de seleccionar una base diferente a la base natural e para la expresión de por vida. La constante de tiempo τ es e −1 -life, el tiempo hasta solo 1/ e permanece, alrededor del 36,8 %, en lugar del 50 % en la vida media de un radionúclido. Por lo tanto, τ es más largo que t1/2. Se puede demostrar que la siguiente ecuación es válida:
- N()t)=N0e− − t/τ τ =N02− − t/t1/2.{displaystyle N(t)=N_{0},e^{-t/tau }=N_{0},2^{-t/t_{1/2},!
Dado que la desintegración radiactiva es exponencial con una probabilidad constante, cada proceso podría describirse fácilmente con un período de tiempo constante diferente que (por ejemplo) dio su "(1/3) vida útil" (cuánto tiempo hasta que solo quede 1/3) o "(1/10)-life" (un período de tiempo hasta que solo quede el 10%), y así sucesivamente. Así, la elección de τ y t1/2 para marcadores-tiempos, son solo por conveniencia y por convención. Reflejan un principio fundamental solo en la medida en que muestran que la misma proporción de una sustancia radiactiva determinada se desintegrará, durante cualquier período de tiempo que se elija.
Matemáticamente, la vida nth para la situación anterior se encontraría de la misma manera que la anterior: mediante configurando N = N0/n, t = T1/n y sustituyendo en la solución de descomposición para obtener
- t1/n=In nλ λ =τ τ In n.{displaystyle t_{1/n}={frac {ln n}=tau ln n.}
Ejemplo para carbono-14
El carbono 14 tiene una vida media de 5700(30) años y una tasa de descomposición de 14 desintegraciones por minuto (dpm) por gramo de carbono natural.
Si se encuentra que un artefacto tiene una radiactividad de 4 dpm por gramo de su C actual, podemos encontrar la edad aproximada del objeto usando la ecuación anterior:
- N=N0e− − t/τ τ ,{displaystyle No.
donde:
- NN0=4/14.. 0,286,τ τ =T1/2In 2.. 8267años,t=− − τ τ In NN0.. 10356años.{displaystyle {begin{aligned}{frac} {N}{N_{0}} {=4/14approx 0.286,\\\tau={frac {T_{1/2}{ln 2}}approx 8267{ years}\\tю=-tau ,ln {frac} {N} {N_{0}}approx 10356{text{ years}end{aligned}}}}
Tarifas cambiantes
Se sabe que los modos de decaimiento radiactivo de captura de electrones y conversión interna son ligeramente sensibles a los efectos químicos y ambientales que cambian la estructura electrónica del átomo, lo que a su vez afecta la presencia de 1s y 2s electrones que participan en el proceso de decaimiento. Un pequeño número de nucleidos se ven afectados. Por ejemplo, los enlaces químicos pueden afectar la velocidad de captura de electrones en un grado pequeño (en general, menos del 1 %), dependiendo de la proximidad de los electrones al núcleo. En 7Be se ha observado una diferencia del 0,9% entre las vidas medias en ambientes metálicos y aislantes. Este efecto relativamente grande se debe a que el berilio es un átomo pequeño cuyos electrones de valencia están en orbitales atómicos 2s, que están sujetos a la captura de electrones en 7Be porque (como todos los s orbitales atómicos en todos los átomos) penetran naturalmente en el núcleo.
En 1992, Jung et al. del grupo de investigación de iones pesados de Darmstadt observó una descomposición β− acelerada de 163Dy66+. Aunque el 163Dy neutro es un isótopo estable, el 163Dy66+ totalmente ionizado sufre una descomposición β− en el Conchas K y L hasta 163Ho66+ con una vida media de 47 días.
El renio-187 es otro ejemplo espectacular. 187Re normalmente sufre un decaimiento beta a 187Os con una vida media de 41,6 × 109 años, pero los estudios usan totalmente ionizado 187Los átomos de Re (núcleos desnudos) han descubierto que esto puede disminuir a solo 32,9 años. Esto se atribuye a la "decaimiento β− del estado ligado" del átomo completamente ionizado: el electrón se emite en la "capa K" (1s orbital atómico), que no puede ocurrir para átomos neutros en los que todos los estados ligados bajos están ocupados.
Varios experimentos han descubierto que las tasas de desintegración de otros modos de radioisótopos artificiales y naturales no se ven afectadas, con un alto grado de precisión, por condiciones externas como la temperatura, la presión, el entorno químico y las condiciones eléctricas, magnéticas o campos gravitatorios. Comparación de experimentos de laboratorio durante el último siglo, estudios del reactor nuclear natural de Oklo (que ejemplificó los efectos de los neutrones térmicos en la descomposición nuclear) y observaciones astrofísicas de la disminución de la luminosidad de las supernovas distantes (que ocurrieron muy lejos, por lo que la luz ha tomado un una gran cantidad de tiempo para llegar a nosotros), por ejemplo, indican fuertemente que las tasas de decaimiento no perturbadas han sido constantes (al menos dentro de las limitaciones de pequeños errores experimentales) como una función del tiempo también.
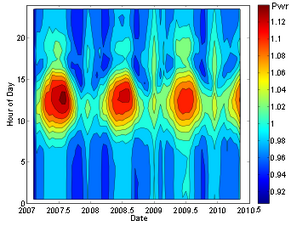
Los resultados recientes sugieren la posibilidad de que las tasas de descomposición tengan una débil dependencia de los factores ambientales. Se ha sugerido que las mediciones de las tasas de descomposición del silicio-32, el manganeso-54 y el radio-226 presentan pequeñas variaciones estacionales (del orden del 0,1%). Sin embargo, tales mediciones son altamente susceptibles a errores sistemáticos, y un artículo posterior no encontró evidencia de tales correlaciones en otros siete isótopos (22Na, 44Ti, 108Ag, 121Sn, 133Ba, 241Am, 238Pu), y conjuntos límites superiores en el tamaño de tales efectos. Una vez se informó que la descomposición del radón-222 exhibía grandes variaciones estacionales de pico a pico del 4% (ver gráfico), que se propusieron estar relacionadas con la actividad de las erupciones solares o la distancia del Sol, pero el análisis detallado del experimento& Los defectos de diseño de #39, junto con las comparaciones con otros experimentos mucho más rigurosos y sistemáticamente controlados, refutan esta afirmación.
Anomalía GSI
Una serie inesperada de resultados experimentales sobre la tasa de desintegración de iones radiactivos pesados altamente cargados que circulan en un anillo de almacenamiento ha provocado actividad teórica en un esfuerzo por encontrar una explicación convincente. Se encuentra que las tasas de desintegración débil de dos especies radiactivas con vidas medias de alrededor de 40 s y 200 s tienen una modulación oscilatoria significativa, con un período de alrededor de 7 s. El fenómeno observado se conoce como anomalía GSI, ya que el anillo de almacenamiento es una instalación en el Centro GSI Helmholtz para la Investigación de Iones Pesados en Darmstadt, Alemania. Como el proceso de decaimiento produce un neutrino electrónico, algunas de las explicaciones propuestas para la tasa de oscilación observada invocan las propiedades de los neutrinos. Las ideas iniciales relacionadas con la oscilación del sabor se encontraron con escepticismo. Una propuesta más reciente implica diferencias de masa entre estados propios de masa de neutrinos.
Base teórica
Los neutrones y protones que constituyen los núcleos, así como otras partículas que se acercan lo suficiente a ellos, se rigen por varias interacciones. La fuerza nuclear (también conocida como fuerza fuerte residual), que no se observa en la escala macroscópica familiar, es la fuerza más poderosa en distancias subatómicas. La fuerza electrostática es casi siempre significativa y, en el caso de la desintegración beta, también interviene la fuerza nuclear débil.
Los efectos combinados de estas fuerzas producen una serie de fenómenos diferentes en los que la energía puede ser liberada por el reordenamiento de las partículas en el núcleo, o bien por el cambio de un tipo de partícula en otros. Estos reordenamientos y transformaciones pueden ser obstaculizados energéticamente para que no ocurran inmediatamente. En ciertos casos, se teoriza que las fluctuaciones aleatorias del vacío cuántico promueven la relajación a un estado de menor energía (el 'decaimiento') en un fenómeno conocido como tunelización cuántica. La vida media de descomposición radiactiva de los nucleidos se midió en escalas de tiempo de 54 órdenes de magnitud, desde 8.6(6)×10−23 segundos (para hidrógeno-5) a 7.10(28)×1031 segundos (para telurio-128). Los límites de estas escalas de tiempo están establecidos únicamente por la sensibilidad de la instrumentación, y no se conocen límites naturales sobre cuán breve o prolongada puede ser la vida media de desintegración radiactiva de un radionúclido.
El proceso de descomposición, como todas las transformaciones de energía impedidas, puede compararse con un campo de nieve en una montaña. Si bien la fricción entre los cristales de hielo puede soportar el peso de la nieve, el sistema es intrínsecamente inestable con respecto a un estado de menor energía potencial. Una perturbación facilitaría así el camino hacia un estado de mayor entropía; el sistema se moverá hacia el estado fundamental, produciendo calor, y la energía total será distribuible en un mayor número de estados cuánticos, lo que resultará en una avalancha. La energía total no cambia en este proceso, pero, debido a la segunda ley de la termodinámica, las avalanchas solo se han observado en una dirección y es hacia el "estado fundamental" — el estado con el mayor número de formas en que podría distribuirse la energía disponible.
Tal colapso (un evento de decaimiento de rayos gamma) requiere una energía de activación específica. Para una avalancha de nieve, esta energía llega como una perturbación desde el exterior del sistema, aunque tales perturbaciones pueden ser arbitrariamente pequeñas. En el caso de un núcleo atómico excitado que se desintegra por la radiación gamma en una emisión espontánea de radiación electromagnética, la perturbación arbitrariamente pequeña proviene de las fluctuaciones del vacío cuántico.
Un núcleo radiactivo (o cualquier sistema excitado en la mecánica cuántica) es inestable y puede, por tanto, espontáneamente estabilizarse en un sistema menos excitado. La transformación resultante altera la estructura del núcleo y da como resultado la emisión de un fotón o una partícula de alta velocidad que tiene masa (como un electrón, una partícula alfa u otro tipo).
Señales de advertencia de peligro
Contenido relacionado
Heptano
Cadaverina
Dinámica


![{displaystyle {begin{aligned}t_{1/2}&={frac {ln(2)}{lambda }}=tau ln(2)\[2pt]A&=-{frac {mathrm {d} N}{mathrm {d} t}}=lambda N={frac {ln(2)}{t_{1/2}}}N\[2pt]S_{A}a_{0}&=-{frac {mathrm {d} N}{mathrm {d} t}}{bigg |}_{t=0}=lambda N_{0}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08fd79adb91a3896db0855d30c72096055431cbf)










![{displaystyle lim _{lambda _{B}rightarrow 0}left[{frac {N_{A0}lambda _{A}}{lambda _{B}-lambda _{A}}}left(e^{-lambda _{A}t}-e^{-lambda _{B}t}right)right]={frac {N_{A0}lambda _{A}}{0-lambda _{A}}}left(e^{-lambda _{A}t}-1right)=N_{A0}left(1-e^{-lambda _{A}t}right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/982ae50245eea1305c63a7b97be54ea1e2a19ccf)

![{displaystyle {begin{aligned}N_{D}&={frac {N_{1}(0)}{lambda _{D}}}sum _{i=1}^{D}lambda _{i}c_{i}e^{-lambda _{i}t}\[3pt]c_{i}&=prod _{j=1,ineq j}^{D}{frac {lambda _{j}}{lambda _{j}-lambda _{i}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd85cd77b00707ebf272a4cb25d5b2768e2ab39)

















![2007 ISO radioactivity hazard symbol intended for IAEA Category 1, 2 and 3 sources defined as dangerous sources capable of death or serious injury[57]](https://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Logo_iso_radiation.svg/120px-Logo_iso_radiation.svg.png)
