Desigualdad triangular

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Propiedad de geometría, también utilizada para generalizar la noción de "distancia" en espacios métricos

Tres ejemplos de la desigualdad triángulo para triángulos con lados de longitudes

x

Sí.

z

. El ejemplo superior muestra un caso donde

z

es mucho menos que la suma

x + Sí.

de los otros dos lados, y el ejemplo inferior muestra un caso donde el lado

z

es sólo un poco menos que

x + Sí.

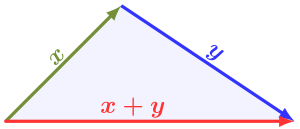
En matemáticas, la desigualdad del triángulo establece que para cualquier triángulo, la suma de las longitudes de dos lados cualesquiera debe ser mayor o igual que la longitud del lado restante. Esta afirmación permite la inclusión de triángulos degenerados, pero algunos autores, especialmente los que escriben sobre geometría elemental, excluirán esta posibilidad, dejando así fuera la posibilidad de igualdad. Si $x$ , $y$ y $z$ son las longitudes de los lados del triángulo, sin que ningún lado sea mayor que $z$ , entonces la desigualdad triangular establece que

zleq x+y,

con igualdad solo en el caso degenerado de un triángulo con área cero. En geometría euclidiana y algunas otras geometrías, la desigualdad triangular es un teorema sobre distancias, y se escribe usando vectores y longitudes de vectores (normas):

|mathbf {x} +mathbf {y} |leq |mathbf {x} |+|mathbf {y} |,

donde la longitud $z$ del tercer lado ha sido reemplazada por el vector suma $x + y$ . Cuando $x$ y $y$ son números reales, se pueden ver como vectores en $R 1$ , y la desigualdad triangular expresa una relación entre valores absolutos.

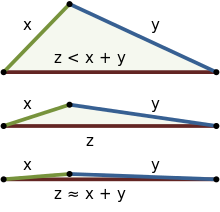
En geometría euclidiana, para triángulos rectángulos la desigualdad triangular es una consecuencia del teorema de Pitágoras, y para triángulos en general, una consecuencia de la ley de los cosenos, aunque puede demostrarse sin estos teoremas. La desigualdad se puede ver intuitivamente en $R 2$ o $R 3$ . La figura de la derecha muestra tres ejemplos que comienzan con una clara desigualdad (arriba) y se acercan a la igualdad (abajo). En el caso euclidiano, la igualdad ocurre solo si el triángulo tiene un ángulo $180°$ y dos ángulos $0°$ , haciendo que los tres vértices colineal, como se muestra en el ejemplo inferior. Así, en geometría euclidiana, la distancia más corta entre dos puntos es una línea recta.

En geometría esférica, la distancia más corta entre dos puntos es un arco de círculo máximo, pero la desigualdad del triángulo se mantiene siempre que se establezca la restricción de que la distancia entre dos puntos en una esfera es la longitud de un segmento de línea esférica menor (es decir, uno con ángulo central en $[0, π]$ ) con esos extremos.

La desigualdad triangular es una propiedad definitoria de normas y medidas de distancia. Esta propiedad debe establecerse como un teorema para cualquier función propuesta a tales efectos para cada espacio en particular: por ejemplo, espacios como los números reales, los espacios euclidianos, los espacios Lp ( $p \geq 1$ ) y espacios de productos internos.

Geometría euclidiana

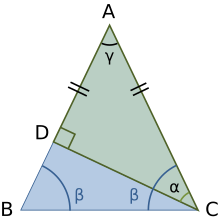
La construcción de Euclid para la prueba de la desigualdad del triángulo para la geometría plana.

Euclides demostró la desigualdad del triángulo para distancias en geometría plana usando la construcción de la figura. Comenzando con el triángulo $ABC$ , se construye un triángulo isósceles con un lado tomado como $BC$ y el otro cateto igual $BD$ a lo largo de la extensión del lado $AB . Entonces se argumenta que el ángulo β tiene una medida mayor que el ángulo α, entonces el lado AD es más largo que el lado AC . Pero AD = AB + BD = AB + BC, por lo que la suma de las longitudes de los lados AB y BC es mayor que la longitud de AC . Esta prueba aparece en los Elementos de Euclides, Libro 1, Proposición 20.$

Expresión matemática de la restricción sobre los lados de un triángulo

Para un triángulo propio, la desigualdad del triángulo, tal como se expresa en palabras, se traduce literalmente en tres desigualdades (dado que un triángulo propio tiene longitudes de lado $a$ , $b$ , $c$ que son todos positivos y excluye el caso degenerado de área cero):

c,quad b+c>a,quad c+a>b.}" xmlns="http://www.w3.org/1998/Math/MathML">a+b■c,b+c■a,c+a■b.{displaystyle a+b confidencial,quad b+c]a,quad c+a títulob.}c,quad b+c>a,quad c+a>b." aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/109c1c77f5f1a29d0af753083dd25d2f3ff6ddd4" style="vertical-align: -0.671ex; width:34.879ex; height:2.509ex;"/>

Se puede demostrar que una forma más sucinta de este sistema de desigualdad es

<math alttext="{displaystyle |a-b|<c Silencioa- - bSilencio.c.a+b.{displaystyle tencióna-b confidenciales seleccionados)a+b.} <img alt="|a-b|<c

Otra forma de decirlo es

<math alttext="{displaystyle max(a,b,c)

max()a,b,c).a+b+c− − max()a,b,c){displaystyle max(a,b,c) se realizó a+b+c-max(a,b,c)}<img alt="max(a,b,c)

lo que implica

<math alttext="{displaystyle 2max(a,b,c)

2max()a,b,c).a+b+c{displaystyle 2max(a,b,c)<img alt="2max(a,b,c)

y por lo tanto que la longitud del lado más largo es menor que el semiperímetro.

Una formulación matemáticamente equivalente es que el área de un triángulo con lados a, b, c debe ser un número real mayor que cero. La fórmula de Heron para el área es

{displaystyle {begin{aligned}4cdot {text{area}}&={sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\&={sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}}}.end{aligned}}}

En términos de cualquiera de las expresiones del área, la desigualdad triangular impuesta en todos los lados es equivalente a la condición de que la expresión debajo del signo de la raíz cuadrada sea real y mayor que cero (por lo que la expresión del área es real y mayor que cero).

La desigualdad triángulo proporciona dos restricciones más interesantes para los triángulos cuyos lados son a, b, c, donde a ≥ b ≥ c y $phi$ es la relación de oro, como

<math alttext="{displaystyle 1<{frac {a+c}{b}}1.a+cb.3{displaystyle 1 {a+c}{b} {3}<img alt="{displaystyle 1<{frac {a+c}{b}}

<math alttext="{displaystyle 1leq min left({frac {a}{b}},{frac {b}{c}}right)1≤ ≤ min()ab,bc).φ φ .{displaystyle 1leq min left({frac {a}},{frac {b}{c}}right) significaphi.}<img alt="{displaystyle 1leq min left({frac {a}{b}},{frac {b}{c}}right)

Triángulo rectángulo

triángulo Isosceles con lados iguales

AB = AC

dividido en dos triángulos rectos por una altitud extraída de uno de los dos ángulos base.

En el caso de los triángulos rectángulos, la desigualdad triangular se especializa en la afirmación de que la hipotenusa es mayor que cualquiera de los dos lados y menor que su suma.

La segunda parte de este teorema ya está establecida anteriormente para cualquier lado de cualquier triángulo. La primera parte se establece utilizando la figura inferior. En la figura, considere el triángulo rectángulo $ADC$ . Un triángulo isósceles $ABC$ se construye con lados iguales $AB = AC$ . Del postulado del triángulo, los ángulos en el triángulo rectángulo $ADC$ satisfacen:

alpha +gamma =pi /2.

Del mismo modo, en el triángulo isósceles $ABC$ , los ángulos satisfacen:

2beta +gamma =pi .

Por lo tanto,

alpha =pi /2-gamma mathrm {while} beta =pi /2-gamma /2

y así, en particular,

<math alttext="{displaystyle alpha α α .β β .{displaystyle alpha = beta .} <img alt="alpha

Eso significa que el lado $AD$ del ángulo opuesto $α$ es más corto que el lado $AB$ opuesto al ángulo mayor $β$ . Pero $AB = AC$ . Por lo tanto:

{overline {mathrm {AD} }}.}" xmlns="http://www.w3.org/1998/Math/MathML">AC̄ ̄ ■AD̄ ̄ .{displaystyle {overline {mathrm {}}}} {nMicrom {fnMicrom}}}.}{overline {mathrm {AD} }}." aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0d07f9ace4f015ceb376e1ed5dce0f26b43855c3" style="vertical-align: -0.338ex; width:11.496ex; height:3.009ex;"/>

Una construcción similar muestra $AC > DC$ , estableciendo el teorema.

Una prueba alternativa (también basada en el postulado del triángulo) procede al considerar tres posiciones para el punto $B$ : (i) como se muestra (que debe probarse), o (ii) $B$ coincidente con $D$ (lo que significaría que el triángulo isósceles tiene dos ángulos rectos como ángulos base más el ángulo del vértice $γ$ , lo que violaría el postulado del triángulo), o por último, (iii) $B$ interior a la derecha triángulo entre los puntos $A$ y $D$ (en cuyo caso el ángulo $ABC$ es un ángulo exterior de un triángulo rectángulo $BDC$ y por lo tanto mayor que $π /2$ , es decir, la otra base ángulo del triángulo isósceles también es mayor que $π /2$ y su suma excede $π$ en violación del postulado del triángulo).

Este teorema que establece las desigualdades es agudizado por Pitágoras' teorema de la igualdad de que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.

Ejemplos de uso

Considere un triángulo cuyos lados están en una progresión aritmética y deje que los lados sean $a$ , $a + d$ , $a + 2 d$ . Entonces la desigualdad triangular requiere que

<math alttext="{displaystyle 0<a0.a.2a+3d{displaystyle 0 realizadasa <img alt="{displaystyle 0<a

<math alttext="{displaystyle 0<a+d0.a+d.2a+2d{displaystyle 0,2d <img alt="{displaystyle 0<a+d

<math alttext="{displaystyle 0<a+2d0.a+2d.2a+d.{displaystyle 0 0 0 0 2d 02a+d.} <img alt="{displaystyle 0<a+2d

Para satisfacer todas estas desigualdades se requiere

0{text{ and }}-{frac {a}{3}}<da■0y− − a3.d.a.{displaystyle a confiado0{text{ y }}-{frac Se hizo.0{text{ and }}-{frac {a}{3}}<d

Cuando se elige $d$ tal que $d = a /3$ , genera un triángulo rectángulo que siempre es similar a la terna pitagórica con lados $3$ , $4, 5 .$

Ahora considere un triángulo cuyos lados están en una progresión geométrica y deje que los lados sean $a$ , $ar$ , $ar 2$ . Entonces la desigualdad triangular requiere que

<math alttext="{displaystyle 0<a0.a.ar+ar2{displaystyle 0 se hizo realidadar+ar^{2}<img alt="{displaystyle 0<a

<math alttext="{displaystyle 0<ar

0.ar.a+ar2{displaystyle 0 ordenadosa+ar^{2}<img alt="{displaystyle 0<ar

<math alttext="{displaystyle 0<ar^{2}

0.ar2.a+ar.{displaystyle 0 ordenadosar^{2}¡Seguido!<img alt="{displaystyle 0<ar^{2}

La primera desigualdad requiere $a > 0$ ; en consecuencia, puede dividirse y eliminarse. Con $a > 0$ , la desigualdad del medio solo requiere $r > 0$ . Esto ahora deja la primera y tercera desigualdades que necesitan satisfacer

0\r^{2}-r-1&{}r2+r− − 1■0r2− − r− − 1.0.{displaystyle {begin{aligned}r^{2}+r-1 limitada{}}0\r^{2}-r-1 limitada{} 0}end{aligned}}}0\r^{2}-r-1&{}

La primera de estas desigualdades cuadráticas requiere que $r$ oscile en la región más allá del valor de la raíz positiva de la ecuación cuadrática $r 2 + r - 1 = 0$ , es decir, $r > φ - 1$ donde $φ$ es la proporción áurea. La segunda desigualdad cuadrática requiere que $r$ oscile entre 0 y la raíz positiva de la ecuación cuadrática $r 2 - r - 1 = 0$ , es decir, $0 < r < φ$ . Los requisitos combinados dan como resultado que $r$ se limite al rango

<math alttext="{displaystyle varphi -1<r0.}" xmlns="http://www.w3.org/1998/Math/MathML">φ φ − − 1.r.φ φ ya■0.{displaystyle varphi -1 Seleccionadovarphi ,{text{ y }]a confianza0.}<img alt="{displaystyle varphi -1<r0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3e74742556d6dabf681246e5fc50b1a9ae4c58af" style="vertical-align: -0.838ex; width:25.722ex; height:2.676ex;"/>

Cuando $r$ la relación común se elige de tal manera que $r = \sqrt φ$ genera un triángulo rectángulo que siempre es similar al triángulo de Kepler.

Generalización a cualquier polígono

La desigualdad del triángulo se puede extender por inducción matemática a caminos poligonales arbitrarios, mostrando que la longitud total de tal camino no es menor que la longitud de la línea recta entre sus extremos. En consecuencia, la longitud de cualquier lado del polígono siempre es menor que la suma de las longitudes de los otros lados del polígono.

Ejemplo de desigualdad poligonal generalizada para un cuadrilátero

Considere un cuadrilátero cuyos lados están en una progresión geométrica y deje que los lados sean $a$ , $ar$ , $ar 2$ , $ar 3$ . Entonces la desigualdad poligonal generalizada requiere que

<math alttext="{displaystyle 0<a0.a.ar+ar2+ar3{displaystyle 0 se hizo realidadar+ar^{2}+ar^{3}<img alt="{displaystyle 0<a

<math alttext="{displaystyle 0<ar

0.ar.a+ar2+ar3{displaystyle 0 ordenadosa+ar^{2}+ar^{3}<img alt="{displaystyle 0<ar

<math alttext="{displaystyle 0<ar^{2}

0.ar2.a+ar+ar3{displaystyle 0 ordenadosar^{2}¡Seguido!<img alt="{displaystyle 0<ar^{2}

<math alttext="{displaystyle 0<ar^{3}

0.ar3.a+ar+ar2.{displaystyle 0 ordenadosar^{3}Selecciona+ar+ar^{2}<img alt="{displaystyle 0<ar^{3}

Estas desigualdades para $a > 0$ reducir a lo siguiente

0}" xmlns="http://www.w3.org/1998/Math/MathML">r3+r2+r− − 1■0{displaystyle r^{3}+r^{2}+r-1 título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9cb6a6872f3f738c8720148a82957e5a52702461" style="vertical-align: -0.505ex; width:19.199ex; height:2.843ex;"/>

<math alttext="{displaystyle r^{3}-r^{2}-r-1r3− − r2− − r− − 1.0.{displaystyle - ¿Qué?<img alt="{displaystyle r^{3}-r^{2}-r-1

Los polinomios del lado izquierdo de estas dos desigualdades tienen raíces que son la constante tribonacci y su recíproco. En consecuencia, $r$ está limitado al rango $1/ t < r < t$ donde $t$ es la constante tribonacci.

Relación con los caminos más cortos

La longitud del arco de una curva se define como el límite inferior superior de las longitudes de aproximaciones poligonales.

Esta generalización se puede usar para demostrar que la curva más corta entre dos puntos en la geometría euclidiana es una línea recta.

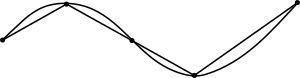
Ningún camino poligonal entre dos puntos es más corto que la línea entre ellos. Esto implica que ninguna curva puede tener una longitud de arco menor que la distancia entre sus extremos. Por definición, la longitud del arco de una curva es el límite superior mínimo de las longitudes de todas las aproximaciones poligonales de la curva. El resultado de las rutas poligonales muestra que la línea recta entre los puntos finales es la más corta de todas las aproximaciones poligonales. Debido a que la longitud del arco de la curva es mayor o igual que la longitud de cada aproximación poligonal, la curva en sí no puede ser más corta que la línea recta.

Conversar

El inverso del teorema de la desigualdad del triángulo también es cierto: si tres números reales son tales que cada uno es menor que la suma de los otros, entonces existe un triángulo con estos números como longitudes de sus lados y con área positiva; y si un número es igual a la suma de los otros dos, existe un triángulo degenerado (es decir, con área cero) con estos números como longitudes de sus lados.

En cualquier caso, si las longitudes de los lados son a, b, c podemos intentar colocar un triángulo en el plano euclidiano como se muestra en el diagrama. Necesitamos probar que existe un número real h consistente con los valores a, b, y c, en cuyo caso existe este triángulo.

Triángulo con altitud

h

base de corte

c

d + c - d)

Por el teorema de Pitágoras tenemos $b 2 = h 2 + d 2$ y $a 2 = h 2 + (c - d) 2$ según la figura en la derecha. Restando estos rendimientos $a 2 - b 2 = c 2 - 2 cd$ . Esta ecuación nos permite expresar $d$ en términos de los lados del triángulo:

d=frac{-a^2+b^2+c^2}{2c}.

Para la altura del triángulo tenemos que $h 2 = b 2 - d 2$ . Al reemplazar $d$ con la fórmula anterior, tenemos

{displaystyle h^{2}=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}.}

Para un número real h para satisfacer esto, $h^{2}$ debe ser no negativo:

{displaystyle b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}geq 0,}

{displaystyle left(b-{frac {-a^{2}+b^{2}+c^{2}}{2c}}right)left(b+{frac {-a^{2}+b^{2}+c^{2}}{2c}}right)geq 0,}

{displaystyle left(a^{2}-(b-c)^{2})((b+c)^{2}-a^{2}right)geq 0,}

{displaystyle (a+b-c)(a-b+c)(b+c+a)(b+c-a)geq 0,}

{displaystyle (a+b-c)(a+c-b)(b+c-a)geq 0,}

que se cumple si la desigualdad del triángulo se cumple para todos los lados. Por lo tanto existe un número real h consistente con los lados a, b, c, y existe el triángulo. Si cada desigualdad triangular se cumple estrictamente, h > 0 y el triángulo no es degenerado (tiene área positiva); pero si una de las desigualdades se cumple con igualdad, entonces h = 0, el triángulo es degenerado.

Generalización a dimensiones superiores

El área de una cara triangular de un tetraedro es menor o igual a la suma de las áreas de las otras tres caras triangulares. De manera más general, en el espacio euclidiano, el hipervolumen de una faceta $(n - 1)$ de una $n$ -simplex es menor o igual que la suma de los hipervolúmenes de las otras $n$ facetas.

Al igual que la desigualdad triangular se generaliza a una desigualdad poligonal, la desigualdad para un símplex de cualquier dimensión se generaliza a un politopo de cualquier dimensión: el hipervolumen de cualquier faceta de un politopo es menor o igual a la suma de los hipervolúmenes de las facetas restantes.

En algunos casos, la desigualdad tetraédrica es más fuerte que varias aplicaciones de la desigualdad triangular. Por ejemplo, la desigualdad triangular parece permitir la posibilidad de cuatro puntos $A$ , $B$ , $C$ y $Z$ en el espacio euclidiano tal que las distancias

AB = BC = CA = 26

AZ = BZ = CZ = 14

Sin embargo, los puntos con tales distancias no pueden existir: el área del triángulo equilátero 26–26–26 $ABC$ es $169 \sqrt 3$ , que es mayor que tres veces $39 \sqrt 3$ , el área de un triángulo isósceles 26–14–14 (todo por la fórmula de Heron), por lo que el arreglo está prohibido por la desigualdad tetraédrica.

Espacio vectorial normado

Triángulo desigualdad para las normas de los vectores.

En un espacio vectorial normado $V$ , una de las propiedades definitorias de la norma es la desigualdad triangular:

{displaystyle |x+y|leq |x|+|y|quad forall ,x,yin V}

es decir, la norma de la suma de dos vectores es en lo más grande como la suma de las normas de los dos vectores. This is also referred to as subadditivity. Para cualquier función propuesta para comportarse como norma, debe satisfacer este requisito. Si el espacio normal es euclidiano, o, más generalmente, estrictamente convexo, entonces $|x+y|=|x|+|y|$ si sólo si el triángulo formado por $x$ , $Sí.$ , y $x + Sí.$ , es degenerado, es decir, $x$ y $Sí.$ están en el mismo rayo, es decir, $x = 0$ o $Sí. = 0$ , o $x = α y$ para algunos $α ■ 0$ . Esta propiedad caracteriza espacios estrictamente convexos, como el $l p$ espacios con $1 p ■$ . Sin embargo, hay espacios ordenados en los que esto es No es verdad. Por ejemplo, considere el avión con el $l 1$ norma (la distancia de Manhattan) y denota $x = (1, 0)$ y $Sí. = (0, 1)$ . Luego el triángulo formado por $x$ , $Sí.$ , y $x + Sí.$ , no es degenerado pero

|x+y|=|(1,1)|=|1|+|1|=2=|x|+|y|.

Normas de ejemplo

Valor absoluto como norma para la línea real. Para ser una norma, la desigualdad triángulo requiere que el valor absoluto satisfaga para cualquier número real $x$ y $Sí.$ : ${displaystyle |x+y|leq |x|+|y|,}$ que hace.

Prueba:

{displaystyle -leftvert xrightvert leq xleq leftvert xrightvert }

{displaystyle -leftvert yrightvert leq yleq leftvert yrightvert }

Después de agregar,

{displaystyle -(leftvert xrightvert +leftvert yrightvert)leq x+yleq leftvert xrightvert +leftvert yrightvert }

Use el hecho de que ${displaystyle leftvert brightvert leq aLeftrightarrow -aleq bleq a}$ (con b sustituido por x+Sí. y a por ${displaystyle leftvert xrightvert +leftvert yrightvert }$ ), tenemos

{displaystyle |x+y|leq |x|+|y|}

La desigualdad triangular es útil en el análisis matemático para determinar la mejor estimación superior del tamaño de la suma de dos números, en términos de los tamaños de los números individuales.

También hay una estimación más baja, que se puede encontrar usando la desigualdad del triángulo inverso que establece que para cualquier número real $x$ y $y$ :

{displaystyle |x-y|geq {biggl |}|x|-|y|{biggr |}.}

Producto interior como norma en un espacio interior de producto. Si la norma surge de un producto interior (como es el caso de los espacios euclidianos), entonces la desigualdad del triángulo se deriva de la desigualdad Cauchy-Schwarz como sigue: Dados vectores $x$ y $y$ , y denotar el producto interno como ${displaystyle langle x,yrangle }$ :

$\|x+y\|^{2}$	$=langle x+y,x+yrangle$
	$=\|x\|^{2}+langle x,yrangle +langle y,xrangle +\|y\|^{2}$
	$leq \|x\|^{2}+2\|langle x,yrangle \|+\|y\|^{2}$
	$leq \|x\|^{2}+2\|x\|\|y\|+\|y\|^{2}$ (por la desigualdad Cauchy-Schwarz)
	$=left(\|x\|+\|y\|right)^{2}$ .

La desigualdad Cauchy-Schwarz se convierte en igualdad si y sólo si $x$ y $Sí.$ dependen linealmente. La desigualdad ${displaystyle langle x,yrangle +langle y,xrangle leq 2left|leftlangle x,yrightrangle right|}$ se convierte en una igualdad de dependencia lineal $x$ y $y$ si y sólo si uno de los vectores $x$ o $Sí.$ es un no negativo Escalar del otro.

Tomar la raíz cuadrada del resultado final da la desigualdad del triángulo.

p-norm: una norma comúnmente utilizada es la p-norm: ${displaystyle |x|_{p}=left(sum _{i=1}^{n}|x_{i}|^{p}right)^{1/p}}$ Donde $x i$ son los componentes del vector $x$ . Para $p = 2$ el $p$ - El ronmo se convierte en Regla de Euclidea: ${displaystyle |x|_{2}=left(sum _{i=1}^{n}|x_{i}|^{2}right)^{1/2}=left(sum _{i=1}^{n}x_{i}^{2}right)^{1/2}}$ que es el teorema de Pitágoras $n$ -dimensiones, un caso muy especial correspondiente a una norma de producto interior. Excepto el caso $p = 2$ , el $p$ -No hay problema. no una norma de producto interior, porque no satisface la ley paralelograma. La desigualdad del triángulo para los valores generales $p$ se llama la desigualdad de Minkowski. Toma la forma: ${displaystyle |x+y|_{p}leq |x|_{p}+|y|_{p}.}$

Espacio métrico

En un espacio métrico $M$ con métrica $d$ , la desigualdad del triángulo es un requisito sobre la distancia:

d(x, z)leq d(x, y)+d(y, z)

para todos $x$ , $y$ , $z$ en $M$ . Es decir, la distancia de $x$ a $z$ es como máximo tan grande como la suma de la distancia desde $x$ hasta $y$ y la distancia de $y$ a $z$ .

La desigualdad triangular es responsable de la mayor parte de la estructura interesante en un espacio métrico, a saber, la convergencia. Esto se debe a que los requisitos restantes para una métrica son bastante simplistas en comparación. Por ejemplo, el hecho de que cualquier sucesión convergente en un espacio métrico sea una sucesión de Cauchy es una consecuencia directa de la desigualdad del triángulo, porque si elegimos cualquier $x n$ y $x m$ tal que $d (x n, x) < ε /2$ y $d (x m, x) < ε /2$ , donde $ε > 0$ es dado y arbitrario (como en la definición de un límite en un espacio métrico), luego por la desigualdad del triángulo, $d (x n, x m) \leq d (x n, x) + d (x m, x) < ε /2 + ε /2 = ε$ , de modo que la secuencia ${x n}$ es una sucesión de Cauchy, por definición.

Esta versión de la desigualdad triangular se reduce a la mencionada anteriormente en el caso de espacios vectoriales normados donde se induce una métrica a través de $d (x, y) ≔ ‖ x - y ‖$ , con $x - y$ siendo el vector que apunta desde el punto $y$ a $x$ .

Desigualdad del triángulo inverso

La desigualdad del triángulo inverso es una consecuencia elemental de la desigualdad del triángulo que da límites inferiores en lugar de límites superiores. Para la geometría plana, la afirmación es:

Cualquier lado de un triángulo es mayor o igual a la diferencia entre los otros dos lados.

En el caso de un espacio vectorial normado, la declaración es:

{bigg |}|x|-|y|{bigg |}leq |x-y|,

o para espacios métricos, $Silencio d () Sí., x) - d () x, z) d () Sí., z)$ . Esto implica que la norma $|cdot |$ así como la función de distancia ${displaystyle d(x,cdot)}$ son Lipschitz continuo con Lipschitz constante $1$ , y por lo tanto son en particular uniformemente continuos.

La prueba para el triángulo reverso utiliza la desigualdad triángulo regular, y ${displaystyle |y-x|=|{-}1(x-y)|=|{-}1|cdot |x-y|=|x-y|}$ :

|x|=|(x-y)+y|leq |x-y|+|y|Rightarrow |x|-|y|leq |x-y|,

|y|=|(y-x)+x|leq |y-x|+|x|Rightarrow |x|-|y|geq -|x-y|,

La combinación de estas dos declaraciones da:

-|x-y|leq |x|-|y|leq |x-y|Rightarrow {bigg |}|x|-|y|{bigg |}leq |x-y|.

Desigualdad de triángulos por semejanza de coseno

Al aplicar la función coseno a la desigualdad del triángulo y la desigualdad del triángulo inverso para las longitudes de arco y al emplear las fórmulas de suma y resta de ángulos para los cosenos, se sigue inmediatamente que

{displaystyle operatorname {sim} (x,z)geq operatorname {sim} (x,y)cdot operatorname {sim} (y,z)-{sqrt {left(1-operatorname {sim} (x,y)^{2}right)cdot left(1-operatorname {sim} (y,z)^{2}right)}}}

{displaystyle operatorname {sim} (x,z)leq operatorname {sim} (x,y)cdot operatorname {sim} (y,z)+{sqrt {left(1-operatorname {sim} (x,y)^{2}right)cdot left(1-operatorname {sim} (y,z)^{2}right)}},.}

Con estas fórmulas, se necesita calcular una raíz cuadrada para cada triple de vectores ${x, y, z}$ que se examina en lugar de $arccos(sim(x, y))$ para cada par de vectores ${x, y}$ examinados, y podría ser una mejora del rendimiento cuando el número de triples examinados es menos que el número de pares examinados.

Reversión en el espacio de Minkowski

La métrica espacial Minkowski $eta _{mu nu }$ no es positivo-definido, lo que significa que ${displaystyle |x|^{2}=eta _{mu nu }x^{mu }x^{nu }}$ puede tener señal o desaparecer, incluso si el vector x no es cero. Además, si x y Sí. son ambos vectores de tiempo que mienten en el futuro cono de luz, la desigualdad triángulo se invierte:

{displaystyle |x+y|geq |x|+|y|.}

Un ejemplo físico de esta desigualdad es la paradoja de los gemelos en la relatividad especial. La misma forma inversa de la desigualdad se cumple si ambos vectores se encuentran en el cono de luz pasado y si uno o ambos son vectores nulos. El resultado se mantiene en n + 1 dimensiones para cualquier n ≥ 1. Si el plano definido por x e y es similar al espacio (y por lo tanto un subespacio euclidiano), entonces se cumple la desigualdad triangular habitual.

Contenido relacionado

Más resultados...

$\|x+y\|^{2}$	$=langle x+y,x+yrangle$
	$=\|x\|^{2}+langle x,yrangle +langle y,xrangle +\|y\|^{2}$
	$leq \|x\|^{2}+2\|langle x,yrangle \|+\|y\|^{2}$
	$leq \|x\|^{2}+2\|x\|\|y\|+\|y\|^{2}$ (por la desigualdad Cauchy-Schwarz)
	$=left(\|x\|+\|y\|right)^{2}$ .